【名师课件】青岛版六年制四下 9.6 综合练习(23张PPT)
文档属性
| 名称 | 【名师课件】青岛版六年制四下 9.6 综合练习(23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1018.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 10:49:22 | ||
图片预览






文档简介
综合练习
总复习
9
复习导入
知识梳理
巩固练习
课后作业
青岛版(六年制) 数学 四年级 下册
24×x
=24 x
.
=24x
在含有字母的式子里,数字和字母、字母和字母
中间的乘号可以记作“·”,也可以省略不写。
省略乘号时,通常把数字写在字母前面。
用含有字母的式子表示指定的数量,再把字母的
取值代入式中求值。
复习导入
2.63千米=2630米
可以用这个数乘或除以两个单位间的进率,也可
以直接把小数点向右或向左移动相应的位数。
运算律:
加法交换律:a + b = b + a
加法结合律:( a + b ) + c = a + ( b + c )
乘法交换律:a × b = b × a
乘法结合律:( a × b ) × c = a × ( b × c )
乘法分配律:( a + b ) × c = a × c + b × c
知识梳理
笔算小数加减法:
7.2
-6.4 8
首先将小数点对齐(即相同数位对齐),然后按整数加
减法计算法则计算;得数末尾有0,一般要把0去掉。
?
2
.
0
7
.
0
.
小数加减混合运算:
与整数加减混合运算顺序相同,都是按照从左往右的
顺序计算;如果算式中有小括号,先算小括号里面的,
再算小括号外面的。
?
36.7-19.4+35.8
=17.3+35.8
=53.1
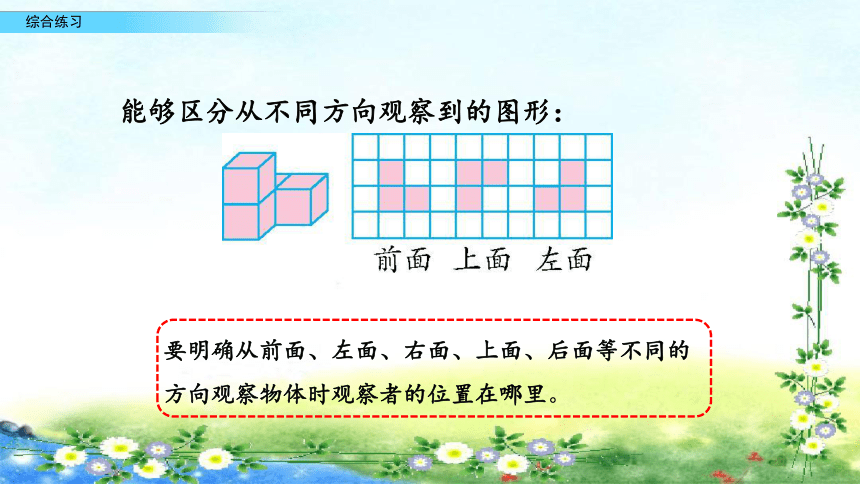
能够区分从不同方向观察到的图形:
要明确从前面、左面、右面、上面、后面等不同的
方向观察物体时观察者的位置在哪里。
?
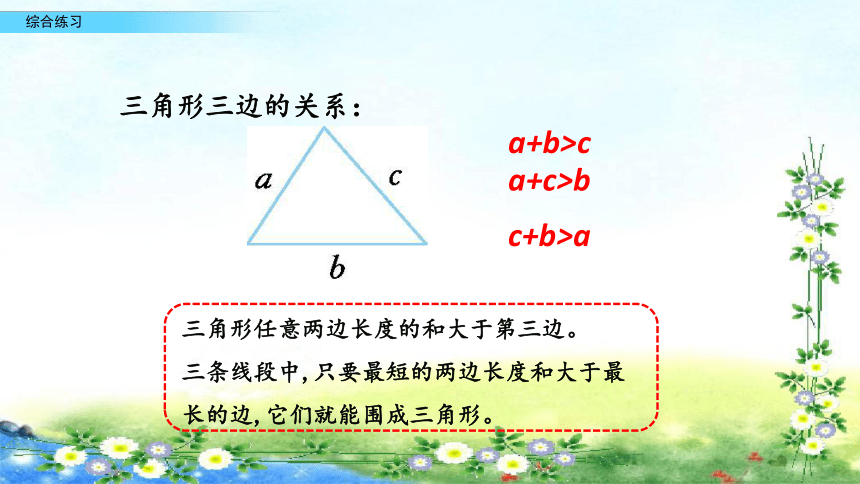
三角形三边的关系:
三角形任意两边长度的和大于第三边。
三条线段中,只要最短的两边长度和大于最长的边,它们就能围成三角形。
a+b>c
a+c>b
c+b>a
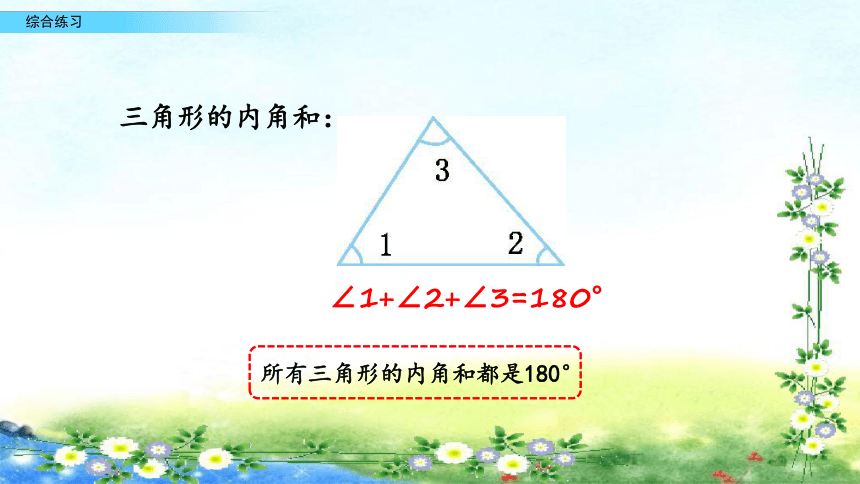
三角形的内角和:
∠1+∠2+∠3=180°
所有三角形的内角和都是180°
平行四边形:
平行四边形的两组对边分别平行且相等,平行四边形
具有易变形的特性。
梯形:
梯形只有一组对边平行,另一组对边不平行。
?
怎么求平均数呢?
一组数据的和除以这组数据的份数所得的商叫这组数据
的平均数。平均数能较好地反映一组数据的整体水平。
先将每个数据依次相加求出全部数据的总和(总数量),
然后利用“总和÷总份数”求出平均数。
下面是小明家、小军家、学校和公园的位置示意图。
(1)从小明家到公园有多少米?
(2)如果小明每分钟走60米,从家到学校需要多少分钟?
从家到公园呢?
a + b
答:从小明家到公园有a+b米。
a ÷ 60
( a + b) ÷ 60
巩固练习
答:从家到学校需要a ÷ 60分钟,从家到公园需要( a + b) ÷ 60分钟。
下面是小明家、小军家、学校和公园的位置示意图。
(3)如果a = 540米,b = 720米,小明家从学校到公园比从学
校回家远多少米?
b - a = 720 – 540 = 180(米)
答:小明家从学校到公园比从学校回家远180米。
下面是小明家、小军家、学校和公园的位置示意图。
(4)小明和小军同时从学校回家。小军每分钟走80米,小明每
分钟走60米,5分钟后两人共走了多远?
(80+60)×5
=140×5
=700(米)
答: 5分钟后两人共走了700米。
填一填。
3.2千米 = ( )米
0.02吨 = ( )千克
480平方厘米 = ( )平方分米
3米5分米 = ( ) 米
3200
20
4.8
3.5
用简便方法计算下面各题。
101×87
700÷25÷4
1.29+3.7+0.71+6.3
25×33×4
=(100+1)×87
=100×87+87
=8700+87
=8787
=(1.29+0.71)+(3.7+6.3)
=2+10
=12
=700÷(25×4)
=700÷100
=7
=25×4×33
=100×33
=3300
出租车司机王师傅一星期行车里程如下。
(1)哪天行驶的路程最长?比最短的多多少千米?
628.1-450.3=177.8(千米)
答:星期六行驶的路程最长,比最短的多177.8千米。
出租车司机王师傅一星期行车里程如下。
(2)平均每天行驶多少千米?(可用计算器计算)
(450.3+501+532.8+494.2+520+628.1+618.6)÷7
=3745÷7
=535(千米)
答:平均每天行驶535千米。
下面两个三角形都是等腰三角形,你能求出∠2的
度数吗?
∠2=180°-35°-35°=110°
∠2=(180°-100°)÷2=40°
画一画。
(1)把下面的平行四边形分成两个梯形。
画一画。
(2)把下面的梯形分成一个平行四边形和一个三角形。
课后作业
1.从教材课后习题中选取;
2.从课时练中选取。
总复习
9
复习导入
知识梳理
巩固练习
课后作业
青岛版(六年制) 数学 四年级 下册
24×x
=24 x
.
=24x
在含有字母的式子里,数字和字母、字母和字母
中间的乘号可以记作“·”,也可以省略不写。
省略乘号时,通常把数字写在字母前面。
用含有字母的式子表示指定的数量,再把字母的
取值代入式中求值。
复习导入
2.63千米=2630米
可以用这个数乘或除以两个单位间的进率,也可
以直接把小数点向右或向左移动相应的位数。
运算律:
加法交换律:a + b = b + a
加法结合律:( a + b ) + c = a + ( b + c )
乘法交换律:a × b = b × a
乘法结合律:( a × b ) × c = a × ( b × c )
乘法分配律:( a + b ) × c = a × c + b × c
知识梳理
笔算小数加减法:
7.2
-6.4 8
首先将小数点对齐(即相同数位对齐),然后按整数加
减法计算法则计算;得数末尾有0,一般要把0去掉。
?
2
.
0
7
.
0
.
小数加减混合运算:
与整数加减混合运算顺序相同,都是按照从左往右的
顺序计算;如果算式中有小括号,先算小括号里面的,
再算小括号外面的。
?
36.7-19.4+35.8
=17.3+35.8
=53.1
能够区分从不同方向观察到的图形:
要明确从前面、左面、右面、上面、后面等不同的
方向观察物体时观察者的位置在哪里。
?
三角形三边的关系:
三角形任意两边长度的和大于第三边。
三条线段中,只要最短的两边长度和大于最长的边,它们就能围成三角形。
a+b>c
a+c>b
c+b>a
三角形的内角和:
∠1+∠2+∠3=180°
所有三角形的内角和都是180°
平行四边形:
平行四边形的两组对边分别平行且相等,平行四边形
具有易变形的特性。
梯形:
梯形只有一组对边平行,另一组对边不平行。
?
怎么求平均数呢?
一组数据的和除以这组数据的份数所得的商叫这组数据
的平均数。平均数能较好地反映一组数据的整体水平。
先将每个数据依次相加求出全部数据的总和(总数量),
然后利用“总和÷总份数”求出平均数。
下面是小明家、小军家、学校和公园的位置示意图。
(1)从小明家到公园有多少米?
(2)如果小明每分钟走60米,从家到学校需要多少分钟?
从家到公园呢?
a + b
答:从小明家到公园有a+b米。
a ÷ 60
( a + b) ÷ 60
巩固练习
答:从家到学校需要a ÷ 60分钟,从家到公园需要( a + b) ÷ 60分钟。
下面是小明家、小军家、学校和公园的位置示意图。
(3)如果a = 540米,b = 720米,小明家从学校到公园比从学
校回家远多少米?
b - a = 720 – 540 = 180(米)
答:小明家从学校到公园比从学校回家远180米。
下面是小明家、小军家、学校和公园的位置示意图。
(4)小明和小军同时从学校回家。小军每分钟走80米,小明每
分钟走60米,5分钟后两人共走了多远?
(80+60)×5
=140×5
=700(米)
答: 5分钟后两人共走了700米。
填一填。
3.2千米 = ( )米
0.02吨 = ( )千克
480平方厘米 = ( )平方分米
3米5分米 = ( ) 米
3200
20
4.8
3.5
用简便方法计算下面各题。
101×87
700÷25÷4
1.29+3.7+0.71+6.3
25×33×4
=(100+1)×87
=100×87+87
=8700+87
=8787
=(1.29+0.71)+(3.7+6.3)
=2+10
=12
=700÷(25×4)
=700÷100
=7
=25×4×33
=100×33
=3300
出租车司机王师傅一星期行车里程如下。
(1)哪天行驶的路程最长?比最短的多多少千米?
628.1-450.3=177.8(千米)
答:星期六行驶的路程最长,比最短的多177.8千米。
出租车司机王师傅一星期行车里程如下。
(2)平均每天行驶多少千米?(可用计算器计算)
(450.3+501+532.8+494.2+520+628.1+618.6)÷7
=3745÷7
=535(千米)
答:平均每天行驶535千米。
下面两个三角形都是等腰三角形,你能求出∠2的
度数吗?
∠2=180°-35°-35°=110°
∠2=(180°-100°)÷2=40°
画一画。
(1)把下面的平行四边形分成两个梯形。
画一画。
(2)把下面的梯形分成一个平行四边形和一个三角形。
课后作业
1.从教材课后习题中选取;
2.从课时练中选取。
同课章节目录
