人教版七年级数学下册7.1平面直角坐标系复习课课件(13张)
文档属性
| 名称 | 人教版七年级数学下册7.1平面直角坐标系复习课课件(13张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 219.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 00:00:00 | ||
图片预览





文档简介
第六章
平面直角坐标系
复面直角坐标系
(一)、回顾本章知识结构:
概念及有关知识
坐标方法的应用
有序数对(a,b)
坐标系画法(坐标、x轴和y轴、象限)
平面上的点
点的坐标
表示地理位置(选、建、标、写)
表示平移(点的平移、图形的平移)
一一对应
(1)点P的坐标是(2,-3),则点P在第
象限;
四
(2)若点P(x,y)的坐标满足
xy﹤0,且在x轴上方,则点P在第
象限;
巩固练习1:由坐标找象限。
温馨提示:判断点的位置,关键抓住象限内点的
坐标的符号特征.
(3)若点A的坐标为(a2+1,
-2–b2),则点A在第____象限.
巩固练习2:坐标轴上点的坐标
(1)点P(m+2,m-1)在x轴上,则点P的坐标是
.
(
3,
0
)
(2)点P(m+2,m-1)在y轴上,则点P的坐标是
.
(
0,
-3
)
(3)点P(x,y)满足
xy=0,
则点P在
.
x
轴上
或
y
轴上
注意:
1.
x轴上的点的纵坐标为0,表示为(x,0),
2.
y轴上的点的横坐标为0,
表示为(0,y)。
原点(0,0)既在x轴上,又在y轴上。
(1).
点(
x,
y
)到
x
轴的距离是
(2).
点(
x,
y
)到
y
轴的距离是
3:点到坐标轴的距离
(1).若点A的坐标是(-
3,
5),则它到x轴的距离是
,到y轴的距离是
.
5
3
(2).点P到x轴、y轴的距离分别是2,1,则点P的坐标可能为
.
(1,2)、
(-1,2)、(-1,-2)
、(1,-2).
巩固练习:
0
1
-1
1
-1
x
y
(0,y)
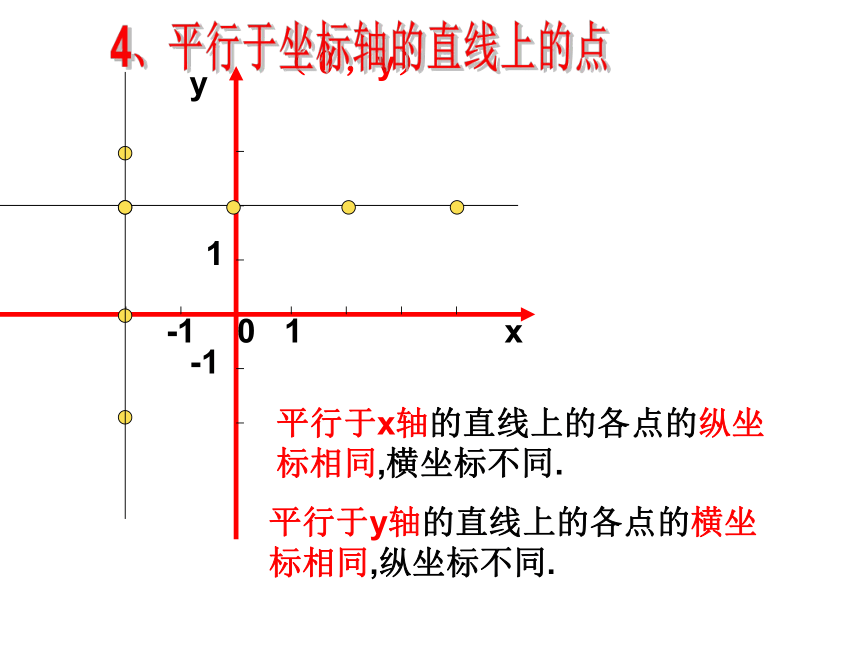
平行于x轴的直线上的各点的纵坐标相同,横坐标不同.
平行于y轴的直线上的各点的横坐标相同,纵坐标不同.
4、平行于坐标轴的直线上的点
中考链接:与坐标轴平行的直线上的点
(1).
已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则m的值为
。
-1
(2).
已知点A(m,-2)、点B(3,m-1),且直线AB∥y轴,则m的值为
。
3
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
x
y
A
B
C
D
5、象限角平分线上的点的坐标特征
(1).
若点P在第一、三象限角的平分线上,则P(
m,
m
).
(2).
若点P在第二、四象限角的平分线上则P(
m,
-m
).
象限角平分线上的点
3.已知点M(a+1,3a-5)每个象限的角平分线上,试求M的坐标.
2.已知点A(2a+1,2+a)在第二象限的平分线上,试求A的坐标.
1.已知点A(2,y
),点B(x
,5
),点A、B在一、三象限的角平分线上,
则x
=____,y
=____;
选取在坐标轴上的边作为三角形的底。
3.已知:A(-3,-2),B(-1,3),C(3,3),
则△
ABC的面积是
。
o
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
x
y
A(-3,-2)
?
?
?
C(3,3)
B(-1,3)
10
H
4
5
4.已知:A(4,2),B(-2,4),C(-2,-1),
则△
ABC的面积是
。
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
A(4,2)
?
?
C(-2,-1)
15
H
B(-2,4)
5
6
一、坐标系中三角形面积的求法
2、三角形无边在坐标轴上或平行于坐标轴
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
5.如图,求△
OAB的面积。
P
平面直角坐标系
复面直角坐标系
(一)、回顾本章知识结构:
概念及有关知识
坐标方法的应用
有序数对(a,b)
坐标系画法(坐标、x轴和y轴、象限)
平面上的点
点的坐标
表示地理位置(选、建、标、写)
表示平移(点的平移、图形的平移)
一一对应
(1)点P的坐标是(2,-3),则点P在第
象限;
四
(2)若点P(x,y)的坐标满足
xy﹤0,且在x轴上方,则点P在第
象限;
巩固练习1:由坐标找象限。
温馨提示:判断点的位置,关键抓住象限内点的
坐标的符号特征.
(3)若点A的坐标为(a2+1,
-2–b2),则点A在第____象限.
巩固练习2:坐标轴上点的坐标
(1)点P(m+2,m-1)在x轴上,则点P的坐标是
.
(
3,
0
)
(2)点P(m+2,m-1)在y轴上,则点P的坐标是
.
(
0,
-3
)
(3)点P(x,y)满足
xy=0,
则点P在
.
x
轴上
或
y
轴上
注意:
1.
x轴上的点的纵坐标为0,表示为(x,0),
2.
y轴上的点的横坐标为0,
表示为(0,y)。
原点(0,0)既在x轴上,又在y轴上。
(1).
点(
x,
y
)到
x
轴的距离是
(2).
点(
x,
y
)到
y
轴的距离是
3:点到坐标轴的距离
(1).若点A的坐标是(-
3,
5),则它到x轴的距离是
,到y轴的距离是
.
5
3
(2).点P到x轴、y轴的距离分别是2,1,则点P的坐标可能为
.
(1,2)、
(-1,2)、(-1,-2)
、(1,-2).
巩固练习:
0
1
-1
1
-1
x
y
(0,y)
平行于x轴的直线上的各点的纵坐标相同,横坐标不同.
平行于y轴的直线上的各点的横坐标相同,纵坐标不同.
4、平行于坐标轴的直线上的点
中考链接:与坐标轴平行的直线上的点
(1).
已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则m的值为
。
-1
(2).
已知点A(m,-2)、点B(3,m-1),且直线AB∥y轴,则m的值为
。
3
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
x
y
A
B
C
D
5、象限角平分线上的点的坐标特征
(1).
若点P在第一、三象限角的平分线上,则P(
m,
m
).
(2).
若点P在第二、四象限角的平分线上则P(
m,
-m
).
象限角平分线上的点
3.已知点M(a+1,3a-5)每个象限的角平分线上,试求M的坐标.
2.已知点A(2a+1,2+a)在第二象限的平分线上,试求A的坐标.
1.已知点A(2,y
),点B(x
,5
),点A、B在一、三象限的角平分线上,
则x
=____,y
=____;
选取在坐标轴上的边作为三角形的底。
3.已知:A(-3,-2),B(-1,3),C(3,3),
则△
ABC的面积是
。
o
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
x
y
A(-3,-2)
?
?
?
C(3,3)
B(-1,3)
10
H
4
5
4.已知:A(4,2),B(-2,4),C(-2,-1),
则△
ABC的面积是
。
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
A(4,2)
?
?
C(-2,-1)
15
H
B(-2,4)
5
6
一、坐标系中三角形面积的求法
2、三角形无边在坐标轴上或平行于坐标轴
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
5.如图,求△
OAB的面积。
P
