2020-2021年北师大版七年级数学下册 4.2 图形的全等课件(30张)
文档属性
| 名称 | 2020-2021年北师大版七年级数学下册 4.2 图形的全等课件(30张) |  | |
| 格式 | pptx | ||
| 文件大小 | 544.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 18:01:38 | ||
图片预览









文档简介
第四章 三角形
图形的全等
学习目标
1.通过实例理解图形全等的概念和特征,并能识别图形的全等.
2.(课标)理解全等三角形的概念,能识别全等三角形中的对应边、对应角.
3.掌握全等三角形对应边相等、对应角相等的性质,并能进行简单的推理和计算,解决一些实际问题.
知识点一:全等图形
一个图形经过平移,翻折,旋转后,位置变化了,但___和___都没有改变,即平移,翻折,旋转前后的图形___________ .
?
知识要点
形状
大小
完全重合
定义
形状、大小相同的图形放在一起能够完全重合.能够完全重合 的两个图形叫做全等形.
1.(1)下列各组图形中,是全等图形的是( )
对点训练
C
(2)对于两个图形,给出下列结论:①两个图形的周长相等;②两个图形的面积相等;③两个图形的周长、面积都相等;④两个图形的形状相同,面积相等.其中能得到这两个图形全等的共有( )
A.1个 B.2个 C.3个 D.4个
A
(1)此题运用定义识别全等图形,确定两个图形全等要符合两个条件:①形状相同,②大小相同;是否是全等图形与位置无关.
(2)判断两个图形是否全等还可以通过平移、旋转、翻折等方法把两个图形叠合在一起,看它们能否完全重合,即用叠合法判断.
小 结
知识点二:全等三角形的相关概念
(1)能够 的两个三角形叫做全等三角形.△ABC与△DEF全等,记作 .?
(2)①对应顶点、对应边及对应角的定义:两个三角形重合时,互相 的顶点叫做对应顶点;互相 的边叫做对应边;互相 的角叫做对应角.记两个三角形全等时,通常把 顶点的字母写在 的位置上.?
对应
对应
重合
重合
重合
△ABC≌△DEF
完全重合
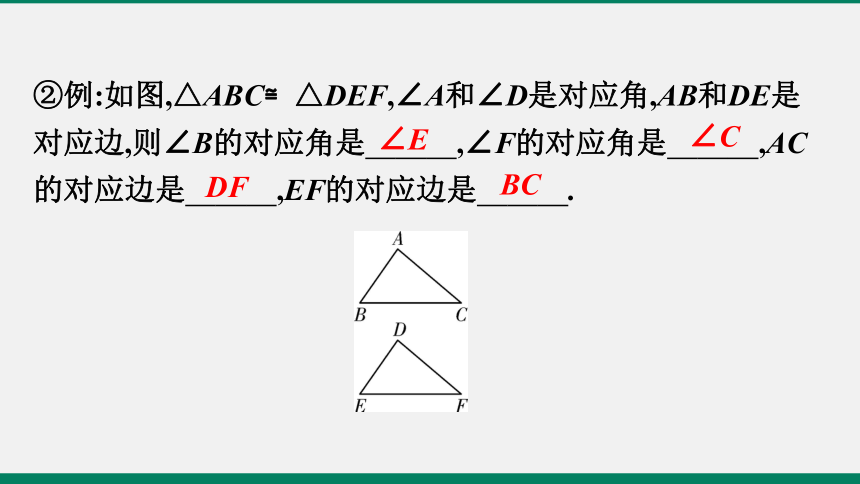
②例:如图,△ABC≌△DEF,∠A和∠D是对应角,AB和DE是对应边,则∠B的对应角是 ,∠F的对应角是 ,AC的对应边是 ,EF的对应边是 .?
BC
DF
∠C
∠E
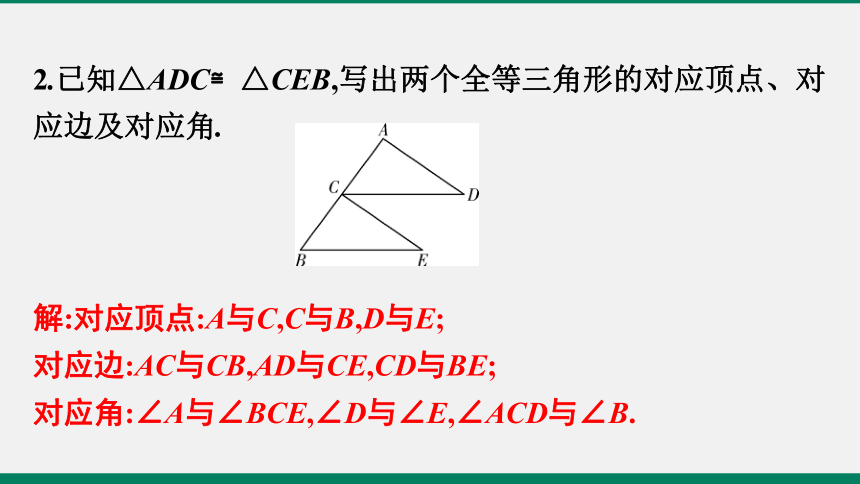
2.已知△ADC≌△CEB,写出两个全等三角形的对应顶点、对应边及对应角.
解:对应顶点:A与C,C与B,D与E;
对应边:AC与CB,AD与CE,CD与BE;
对应角:∠A与∠BCE,∠D与∠E,∠ACD与∠B.
利用图形的位置特征确定对应边和对应角时,要抓住对应边所对的角是对应角,对应角所对的边是对应边,两对应边的夹角是对应角,两对应角的夹边是对应边;当全等三角形的两组对应边(角)已确定时,剩下的一组边(角)就是对应边(角).
小 结
写出其中相等的角:
, , ;?
写出其中相等的边:
, , .?
OA=OC
OD=OB
AD=CB
∠AOD=∠COB
∠D=∠B
知识点三:全等三角形的性质
(1)全等三角形的对应边 ,对应角 .?
(2)例:如图,△AOD≌△COB,
∠A=∠C
相等
相等
还具备:全等三角形对应边上的中线相等,对应边上的高相等,对应角平分线相等;全等三角形的周长相等、面积也相等.
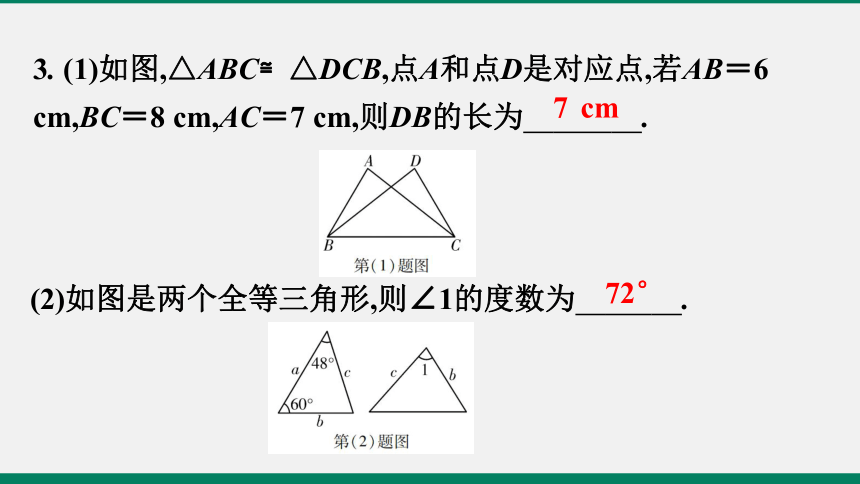
(2)如图是两个全等三角形,则∠1的度数为 .?
3. (1)如图,△ABC≌△DCB,点A和点D是对应点,若AB=6 cm,BC=8 cm,AC=7 cm,则DB的长为 .?
72°
7 cm
4.如图,已知点A,D,B,F在同一条直线上,△ABC≌△FDE,AB=8 cm,BD=6 cm.求FB的长.
由全等三角形的性质知AB=FD,
由等式的性质可得AD=FB,
所以要求FB的长,只需求AD的长.
因为△ABC≌△FDE,所以 AB=FD.
所以 AB-DB=FD-DB,即AD=FB.
因为AB=8 cm,BD=6 cm,
所以AD=AB-DB=8-6=2(cm).
所以FB=AD=2cm.
导引:
解:
(1)全等三角形的性质在几何推理和计算中起着重要
作用,当所求线段不是全等三角形的对应边时,
可利用等式的性质进行转换,从而找到所求线段
与已知线段的关系.
(2)本题利用全等三角形的性质,可把线段AB转化成
线段DF,再利用等式的性质可把求线段FB的长
转化成求线段AD的长.
小 结
5.如图,Rt△ABC≌Rt△CDE,∠B=∠D=90°,且
B,C,D三点在一条直线上,求∠ACE的度数.
要求∠ACE,只需求∠ACB、
∠ECD或∠ACB+∠ECD即可.
由于∠ACB和∠ECD无法求出,
因此必须求∠ACB+∠ECD.
由Rt△ABC≌Rt△CDE,可知∠BAC=∠DCE,
结合直角三角形的两个锐角互余的性质,可求∠ACB
与∠ECD的度数和,再根据平角的定义可求∠ACE的
度数.
导引:
因为Rt△ABC≌Rt△CDE,
所以∠BAC=∠DCE.
又因为在Rt△ABC中,∠B=90°,
所以∠ACB+∠BAC=90°.
所以∠ACB+∠ECD=90°.
所以∠ACE=180°-(∠ACB+∠ECD)
=180°-90°=90°.
解:
(1)利用全等三角形的性质求角的度数的方法:利用
全等三角形的性质先确定两个三角形中角的对应
关系,由这种关系实现已知角和未知角之间的转
换,从而求出所要求的角的度数.
(2)本题主要利用了全等三角形对应角相等的性质,
通过全等三角形把属于两个三角形的∠ACB、
∠ECD联系在一起,并将它们作为一个整体求出
其度数的和.
小 结
6.下列图形中,与已知图形全等的是( )
精典范例
B
A.1对
B.2对
C.3对
D.4对
7.如图,将△ABC沿AC翻折后,点B与点E重合,则图中全等三角形有( )
变式练习
C
8.如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他对应边和对应角.
解:对应边:AN与AM,BN与CM;
对应角:∠BAN与∠CAM,∠ANB与∠AMC.
9.如图,△ABC≌△DBC,且∠A和∠D,∠ABC和∠DBC是对应角,请写出三组对应边:
(1) ;?
(2) ;?
(3) ;?
另一组对应角:(4) .?
∠ACB和∠DCB
BC和BC
AC和DC
AB和DB
A.4 cm
B.3 cm
C.2 cm
D.3.5 cm
10.如图,△ABC≌△EBD,AB=4 cm,BD=7 cm,则CE的长度为( )
B
A.1
B.2
C.2.5
D.3
11.如图,若△ABC≌△DEF,BC=6,EC=4,则CF的长为( )
B
A.150°
B.120°
C.90°
D.60°
12.如图,△ABC≌△A'B'C',其中∠A=36°,
∠C=24°,则∠B'=( )
B
A.35°
B.30°
C.25°
D.20°
13.如图,△ABO≌△DCO,∠D=80°,∠DOC=70°,则∠B=( )
B
14.如图,已知△ABC≌△DEF,B,E,C,F在同一直线上.
(1)若∠BED=130°,∠D=70°,求∠ACB的度数;
(2)若2BE=EC,EC=6,求BF的长.
解:(1)因为∠BED=130°,所以∠DEF=180°-130°=50°.
所以∠F=180°-∠D-∠DEF=180°-70°-50=60°,
因为△ABC≌△DEF,所以∠ACB=∠F=60°.
(2)因为2BE=EC,EC=6,所以BE=3,所以BC=9,
因为△ABC≌△DEF,所以EF=BC=9,
所以BF=EF+BE=12.
★15.如图,已知△ABC≌△FED,AF=8,BE=2.
(1)试说明:AC∥DF;
(2)求AB的长.
解:(1)因为△ABC≌△FED,所以∠A=∠F.所以AC∥DF.
(2)因为△ABC≌△FED,所以AB=EF.
所以AB-EB=EF-EB.所以AE=BF.
因为AF=8,BE=2,所以AE+BF=8-2=6,
所以AE=3,所以AB=AE+BE=3+2=5.
1.全等图形:(1)定义;(2)性质.
2.全等三角形:(1)定义;(2)性质.
3.全等三角形的性质的作用:
(1)求角的度数;(2)说明两个角相等;
(3)求线段的长度;(4)说明两条线段相等;
(5)判断两条直线的位置关系等.
总 结
图形的全等
学习目标
1.通过实例理解图形全等的概念和特征,并能识别图形的全等.
2.(课标)理解全等三角形的概念,能识别全等三角形中的对应边、对应角.
3.掌握全等三角形对应边相等、对应角相等的性质,并能进行简单的推理和计算,解决一些实际问题.
知识点一:全等图形
一个图形经过平移,翻折,旋转后,位置变化了,但___和___都没有改变,即平移,翻折,旋转前后的图形___________ .
?
知识要点
形状
大小
完全重合
定义
形状、大小相同的图形放在一起能够完全重合.能够完全重合 的两个图形叫做全等形.
1.(1)下列各组图形中,是全等图形的是( )
对点训练
C
(2)对于两个图形,给出下列结论:①两个图形的周长相等;②两个图形的面积相等;③两个图形的周长、面积都相等;④两个图形的形状相同,面积相等.其中能得到这两个图形全等的共有( )
A.1个 B.2个 C.3个 D.4个
A
(1)此题运用定义识别全等图形,确定两个图形全等要符合两个条件:①形状相同,②大小相同;是否是全等图形与位置无关.
(2)判断两个图形是否全等还可以通过平移、旋转、翻折等方法把两个图形叠合在一起,看它们能否完全重合,即用叠合法判断.
小 结
知识点二:全等三角形的相关概念
(1)能够 的两个三角形叫做全等三角形.△ABC与△DEF全等,记作 .?
(2)①对应顶点、对应边及对应角的定义:两个三角形重合时,互相 的顶点叫做对应顶点;互相 的边叫做对应边;互相 的角叫做对应角.记两个三角形全等时,通常把 顶点的字母写在 的位置上.?
对应
对应
重合
重合
重合
△ABC≌△DEF
完全重合
②例:如图,△ABC≌△DEF,∠A和∠D是对应角,AB和DE是对应边,则∠B的对应角是 ,∠F的对应角是 ,AC的对应边是 ,EF的对应边是 .?
BC
DF
∠C
∠E
2.已知△ADC≌△CEB,写出两个全等三角形的对应顶点、对应边及对应角.
解:对应顶点:A与C,C与B,D与E;
对应边:AC与CB,AD与CE,CD与BE;
对应角:∠A与∠BCE,∠D与∠E,∠ACD与∠B.
利用图形的位置特征确定对应边和对应角时,要抓住对应边所对的角是对应角,对应角所对的边是对应边,两对应边的夹角是对应角,两对应角的夹边是对应边;当全等三角形的两组对应边(角)已确定时,剩下的一组边(角)就是对应边(角).
小 结
写出其中相等的角:
, , ;?
写出其中相等的边:
, , .?
OA=OC
OD=OB
AD=CB
∠AOD=∠COB
∠D=∠B
知识点三:全等三角形的性质
(1)全等三角形的对应边 ,对应角 .?
(2)例:如图,△AOD≌△COB,
∠A=∠C
相等
相等
还具备:全等三角形对应边上的中线相等,对应边上的高相等,对应角平分线相等;全等三角形的周长相等、面积也相等.
(2)如图是两个全等三角形,则∠1的度数为 .?
3. (1)如图,△ABC≌△DCB,点A和点D是对应点,若AB=6 cm,BC=8 cm,AC=7 cm,则DB的长为 .?
72°
7 cm
4.如图,已知点A,D,B,F在同一条直线上,△ABC≌△FDE,AB=8 cm,BD=6 cm.求FB的长.
由全等三角形的性质知AB=FD,
由等式的性质可得AD=FB,
所以要求FB的长,只需求AD的长.
因为△ABC≌△FDE,所以 AB=FD.
所以 AB-DB=FD-DB,即AD=FB.
因为AB=8 cm,BD=6 cm,
所以AD=AB-DB=8-6=2(cm).
所以FB=AD=2cm.
导引:
解:
(1)全等三角形的性质在几何推理和计算中起着重要
作用,当所求线段不是全等三角形的对应边时,
可利用等式的性质进行转换,从而找到所求线段
与已知线段的关系.
(2)本题利用全等三角形的性质,可把线段AB转化成
线段DF,再利用等式的性质可把求线段FB的长
转化成求线段AD的长.
小 结
5.如图,Rt△ABC≌Rt△CDE,∠B=∠D=90°,且
B,C,D三点在一条直线上,求∠ACE的度数.
要求∠ACE,只需求∠ACB、
∠ECD或∠ACB+∠ECD即可.
由于∠ACB和∠ECD无法求出,
因此必须求∠ACB+∠ECD.
由Rt△ABC≌Rt△CDE,可知∠BAC=∠DCE,
结合直角三角形的两个锐角互余的性质,可求∠ACB
与∠ECD的度数和,再根据平角的定义可求∠ACE的
度数.
导引:
因为Rt△ABC≌Rt△CDE,
所以∠BAC=∠DCE.
又因为在Rt△ABC中,∠B=90°,
所以∠ACB+∠BAC=90°.
所以∠ACB+∠ECD=90°.
所以∠ACE=180°-(∠ACB+∠ECD)
=180°-90°=90°.
解:
(1)利用全等三角形的性质求角的度数的方法:利用
全等三角形的性质先确定两个三角形中角的对应
关系,由这种关系实现已知角和未知角之间的转
换,从而求出所要求的角的度数.
(2)本题主要利用了全等三角形对应角相等的性质,
通过全等三角形把属于两个三角形的∠ACB、
∠ECD联系在一起,并将它们作为一个整体求出
其度数的和.
小 结
6.下列图形中,与已知图形全等的是( )
精典范例
B
A.1对
B.2对
C.3对
D.4对
7.如图,将△ABC沿AC翻折后,点B与点E重合,则图中全等三角形有( )
变式练习
C
8.如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他对应边和对应角.
解:对应边:AN与AM,BN与CM;
对应角:∠BAN与∠CAM,∠ANB与∠AMC.
9.如图,△ABC≌△DBC,且∠A和∠D,∠ABC和∠DBC是对应角,请写出三组对应边:
(1) ;?
(2) ;?
(3) ;?
另一组对应角:(4) .?
∠ACB和∠DCB
BC和BC
AC和DC
AB和DB
A.4 cm
B.3 cm
C.2 cm
D.3.5 cm
10.如图,△ABC≌△EBD,AB=4 cm,BD=7 cm,则CE的长度为( )
B
A.1
B.2
C.2.5
D.3
11.如图,若△ABC≌△DEF,BC=6,EC=4,则CF的长为( )
B
A.150°
B.120°
C.90°
D.60°
12.如图,△ABC≌△A'B'C',其中∠A=36°,
∠C=24°,则∠B'=( )
B
A.35°
B.30°
C.25°
D.20°
13.如图,△ABO≌△DCO,∠D=80°,∠DOC=70°,则∠B=( )
B
14.如图,已知△ABC≌△DEF,B,E,C,F在同一直线上.
(1)若∠BED=130°,∠D=70°,求∠ACB的度数;
(2)若2BE=EC,EC=6,求BF的长.
解:(1)因为∠BED=130°,所以∠DEF=180°-130°=50°.
所以∠F=180°-∠D-∠DEF=180°-70°-50=60°,
因为△ABC≌△DEF,所以∠ACB=∠F=60°.
(2)因为2BE=EC,EC=6,所以BE=3,所以BC=9,
因为△ABC≌△DEF,所以EF=BC=9,
所以BF=EF+BE=12.
★15.如图,已知△ABC≌△FED,AF=8,BE=2.
(1)试说明:AC∥DF;
(2)求AB的长.
解:(1)因为△ABC≌△FED,所以∠A=∠F.所以AC∥DF.
(2)因为△ABC≌△FED,所以AB=EF.
所以AB-EB=EF-EB.所以AE=BF.
因为AF=8,BE=2,所以AE+BF=8-2=6,
所以AE=3,所以AB=AE+BE=3+2=5.
1.全等图形:(1)定义;(2)性质.
2.全等三角形:(1)定义;(2)性质.
3.全等三角形的性质的作用:
(1)求角的度数;(2)说明两个角相等;
(3)求线段的长度;(4)说明两条线段相等;
(5)判断两条直线的位置关系等.
总 结
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
