五年级下册数学课件 《综合与实践:探索图形》人教版 (共25张PPT)
文档属性
| 名称 | 五年级下册数学课件 《综合与实践:探索图形》人教版 (共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 849.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
综合与实践:探索图形
探索图形
人教版数学五年级下册
学习目标
1.通过观察、列表等活动进一步认识和理解正方体特征。
2.经历“找规律”的全过程,获得“化繁为简”的解决问题的策略,积累数学思维的活动经验,培养空间想象能力。
复习旧知
同学们,正方体的面、棱、顶点各有什么特征?
同学们,正方体的表面积和体积都需要许多计算才能得到,但是今天我们不去探讨这个,我们今天来进行一个不需要怎么计算,但是需要发挥你们想象力的小探究,好不好?
探索图形
导入新知
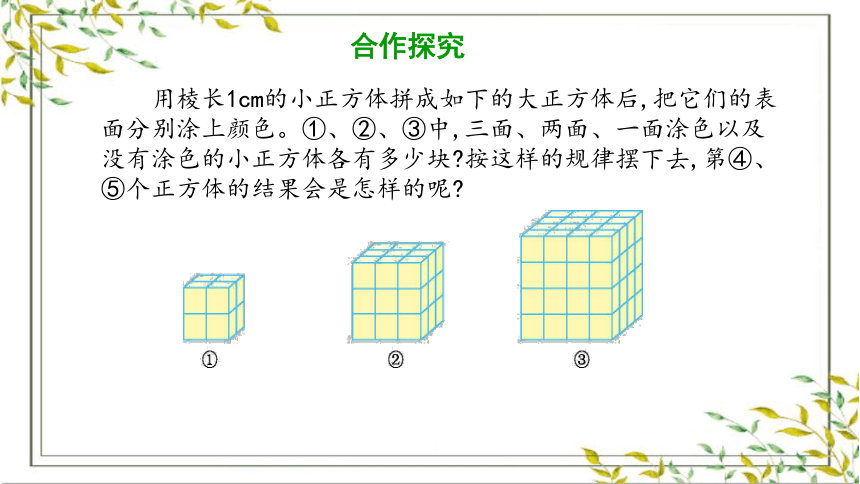
用棱长1cm的小正方体拼成如下的大正方体后,把它们的表面分别涂上颜色。①、②、③中,三面、两面、一面涂色以及没有涂色的小正方体各有多少块?按这样的规律摆下去,第④、⑤个正方体的结果会是怎样的呢?
合作探究
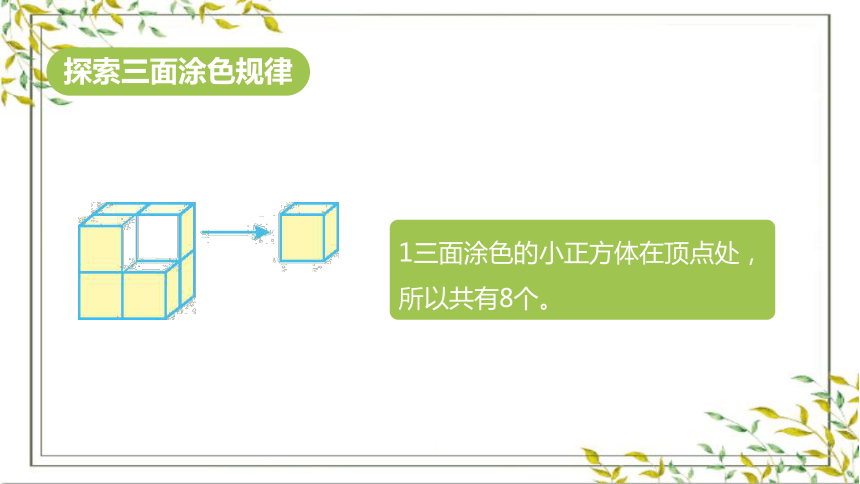
1三面涂色的小正方体在顶点处,
所以共有8个。
探索三面涂色规律
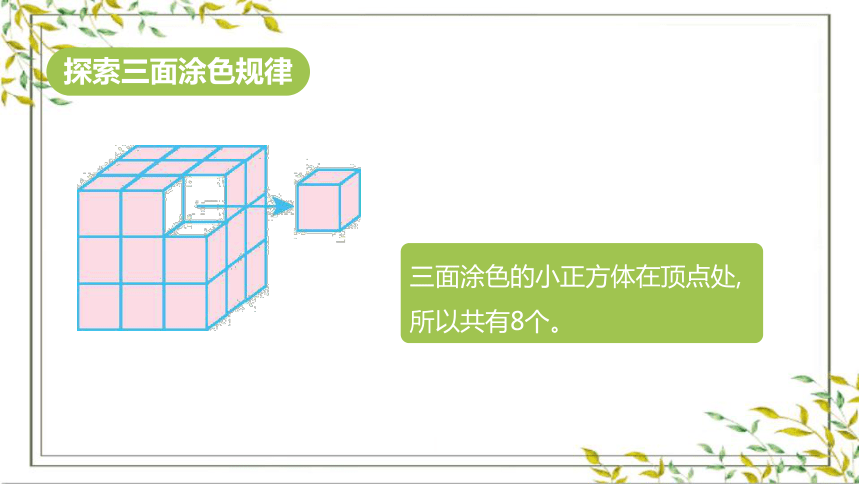
三面涂色的小正方体在顶点处,所以共有8个。
探索三面涂色规律
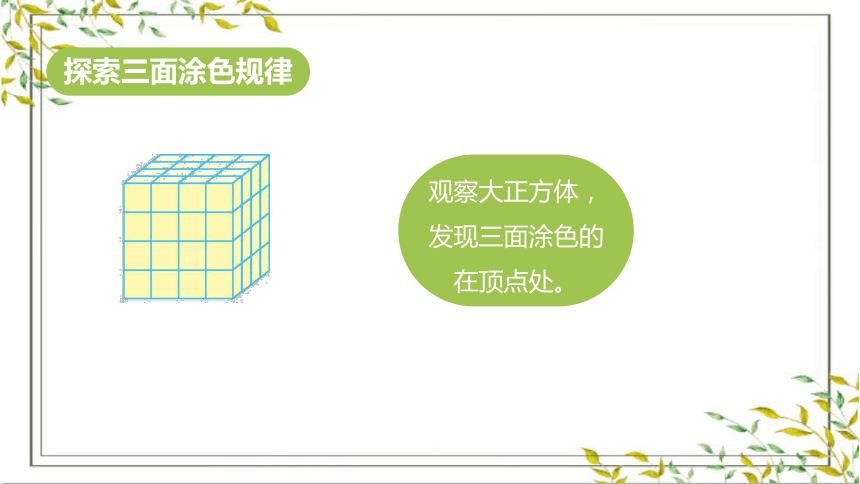
观察大正方体,发现三面涂色的在顶点处。
探索三面涂色规律
三面涂色的规律
总结:
三面涂色的小正方体都在大正方体顶点的位置,都是8块。
两面涂色的小正方体在原正方体的每条棱的中间位置。
探索两面涂色规律
每个正方体有12条棱,所以共有12个。
探索两面涂色规律
因为每条棱分成了4段,有4个小正方体,除去顶点的2个涂了三面,还有2个涂了两面。
每个正方体有12条棱,所以共有24个。
两面涂色的规律
总结:
若每条棱上有n个小方块,两面涂色的是(n-2)×12块。
一面涂色的小正方体在原正方体每个面的中间位置,每个正方体有6个面,所以共有6个。
一面涂色的规律
一面涂色的规律
棱长4厘米的大正方体切成棱长为1厘米的小正方体,每一个面可以切成4个只涂一面的小正方体,6个面一共有24个涂了一面。
一面涂色的规律
总结:
若每条棱上有n个小方块,一面涂色的是(n-2)2×6块。
没有涂色的规律
没有涂色的小正方体在原正方体的中心位置,所以有1个。
没有涂色的规律
把外面2层去掉,剩下中间2层,每层中间都有4个没有涂色的,2层就是8个。
涂色的规律
三面涂色的块数
两面涂色的块数
一面涂色的块数
没有涂色的块数
?
8
0
0
0
?
8
12
6
1
?
8
24
?
?
24
8
8
36
54
27
8
48
96
64
①
②
③
④
⑤
1.如果摆成下面的几何体,你会数吗?
4
10
20
巩固新知
三面涂色:8个
两面涂色:(10-2)×12=96(个)
一面涂色:(10-2)2×6=384(个)
2.有一个棱长为10分米的正方体,它的6个面都涂有黄色,把它分割成棱长为1分米的小正方体若干个。三面涂黄色的小正方体有几个?两面涂黄色的小正方体有几个?一面涂黄色的小正方体有几个?
若每条棱上有n个小方块,三面涂色的是8块,两面涂色的是(n-2)×12,一面涂色的是(n-2)2×6,没有涂色的块数(n-2)3
课堂总结
1.一个正方体,在它的每个面上都涂红色,再把它分割成棱长是1厘米的小正方体若干个。已知两面涂色的小正方体有96个,求大正方体的棱长。
96÷12+2=10(厘米)
课后练习
2.已知一个大正方体木块能被分割成若干个棱长是1厘米的小正方体木块,在这个大正方体木块的6个面上涂红色,把它分割成若干个棱长是1厘米的小正方体木块中,有两面涂红色的共108块,那么只有一面涂红色的有几块?
108÷12+2=11(厘米)
(11-2)2×6=486(块)
3.一个棱长为6厘米的正方体,在它的每个面上都涂红色,把它分割成棱长是1厘米的小正方体若干个。在最上面的一层中,一面、二面和三面涂色的小正方体各有多少个?
三面的:4
个
两面的:(6-2)×4=16(个)
一面的:(6-2)×(6-2)=16(个)
再
见
综合与实践:探索图形
探索图形
人教版数学五年级下册
学习目标
1.通过观察、列表等活动进一步认识和理解正方体特征。
2.经历“找规律”的全过程,获得“化繁为简”的解决问题的策略,积累数学思维的活动经验,培养空间想象能力。
复习旧知
同学们,正方体的面、棱、顶点各有什么特征?
同学们,正方体的表面积和体积都需要许多计算才能得到,但是今天我们不去探讨这个,我们今天来进行一个不需要怎么计算,但是需要发挥你们想象力的小探究,好不好?
探索图形
导入新知
用棱长1cm的小正方体拼成如下的大正方体后,把它们的表面分别涂上颜色。①、②、③中,三面、两面、一面涂色以及没有涂色的小正方体各有多少块?按这样的规律摆下去,第④、⑤个正方体的结果会是怎样的呢?
合作探究
1三面涂色的小正方体在顶点处,
所以共有8个。
探索三面涂色规律
三面涂色的小正方体在顶点处,所以共有8个。
探索三面涂色规律
观察大正方体,发现三面涂色的在顶点处。
探索三面涂色规律
三面涂色的规律
总结:
三面涂色的小正方体都在大正方体顶点的位置,都是8块。
两面涂色的小正方体在原正方体的每条棱的中间位置。
探索两面涂色规律
每个正方体有12条棱,所以共有12个。
探索两面涂色规律
因为每条棱分成了4段,有4个小正方体,除去顶点的2个涂了三面,还有2个涂了两面。
每个正方体有12条棱,所以共有24个。
两面涂色的规律
总结:
若每条棱上有n个小方块,两面涂色的是(n-2)×12块。
一面涂色的小正方体在原正方体每个面的中间位置,每个正方体有6个面,所以共有6个。
一面涂色的规律
一面涂色的规律
棱长4厘米的大正方体切成棱长为1厘米的小正方体,每一个面可以切成4个只涂一面的小正方体,6个面一共有24个涂了一面。
一面涂色的规律
总结:
若每条棱上有n个小方块,一面涂色的是(n-2)2×6块。
没有涂色的规律
没有涂色的小正方体在原正方体的中心位置,所以有1个。
没有涂色的规律
把外面2层去掉,剩下中间2层,每层中间都有4个没有涂色的,2层就是8个。
涂色的规律
三面涂色的块数
两面涂色的块数
一面涂色的块数
没有涂色的块数
?
8
0
0
0
?
8
12
6
1
?
8
24
?
?
24
8
8
36
54
27
8
48
96
64
①
②
③
④
⑤
1.如果摆成下面的几何体,你会数吗?
4
10
20
巩固新知
三面涂色:8个
两面涂色:(10-2)×12=96(个)
一面涂色:(10-2)2×6=384(个)
2.有一个棱长为10分米的正方体,它的6个面都涂有黄色,把它分割成棱长为1分米的小正方体若干个。三面涂黄色的小正方体有几个?两面涂黄色的小正方体有几个?一面涂黄色的小正方体有几个?
若每条棱上有n个小方块,三面涂色的是8块,两面涂色的是(n-2)×12,一面涂色的是(n-2)2×6,没有涂色的块数(n-2)3
课堂总结
1.一个正方体,在它的每个面上都涂红色,再把它分割成棱长是1厘米的小正方体若干个。已知两面涂色的小正方体有96个,求大正方体的棱长。
96÷12+2=10(厘米)
课后练习
2.已知一个大正方体木块能被分割成若干个棱长是1厘米的小正方体木块,在这个大正方体木块的6个面上涂红色,把它分割成若干个棱长是1厘米的小正方体木块中,有两面涂红色的共108块,那么只有一面涂红色的有几块?
108÷12+2=11(厘米)
(11-2)2×6=486(块)
3.一个棱长为6厘米的正方体,在它的每个面上都涂红色,把它分割成棱长是1厘米的小正方体若干个。在最上面的一层中,一面、二面和三面涂色的小正方体各有多少个?
三面的:4
个
两面的:(6-2)×4=16(个)
一面的:(6-2)×(6-2)=16(个)
再
见
