10.5 用二元一次方程组解决问题(第2课时)(共28张PPT)
文档属性
| 名称 | 10.5 用二元一次方程组解决问题(第2课时)(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 00:00:00 | ||
图片预览








文档简介
第2课时
10.5 用二元一次方程组解决问题
第10章 二元一次方程
2020-2021学年度苏科版七年级下册
养牛场原有30只大牛和15只小牛,一天约用饲料675㎏;一周后又购进12只大牛和5只小牛,这时1天约用饲料940㎏.饲养员李大叔估计每只大牛1天约需饲料18~20㎏,每只小牛1天约需饲料7~8㎏.你能否通过计算检验他的估计?
探究1
1、把探究1中表示等量关系的语句画记在课本上,并用等式表示这两个等量关系 .
2、若设每只大牛和每只小牛1天各约用x㎏和y㎏,依据上面等量关系列出方程组,并填在课本上.
3、解二元一次方程组有哪些方法?解所列的方程组有什么技巧?请总结,在练习本上写出解题过程.
4、如何判定饲养员李大叔的估计是否正确?
5、以上问题还能列出不同的二元一次方程组吗?结果是否一致?试一试!
1、把探究1中表示等量关系的语句画记在课本上,并用等式表示这两个等量关系
2、若设每只大牛和每只小牛1天各约用饲料x㎏和y㎏,依据上面等量关系列出方程组,并填在课本上.
(1)30只大牛所用饲料+15只小牛所用饲料=675㎏
(2)42只大牛所用饲料+20只小牛所用饲料=940㎏
30x+15y=675
42x+20y=940
3、解二元一次方程组有哪些方法?解所列的方程
组有什么技巧?请总结,在练习本上写出解题过程.
(1)代入法 (2)加减法
4、如何判定饲养员李大叔的估计是否正确?这就是说,每只大牛1天约需饲料20kg,每只小牛1天约需饲料5kg,因此,饲料李大叔对大牛的食量估计较准确,对小牛的食量估计偏高.
5、以上问题还能列出不同的二元一次方 程组吗?结果是否一致?试一试!
30x+15y=675
12x+5y=265
你知道吗?
列二元一次方程组解决实际问题的步骤:
审:读懂题意,找出题中的两个相等关系;
设:根据题意设上未知数;
列:根据相等关系列方程组;
解:解方程组;
验:检验1、解是否正确,2、解是否符合实
际意义;
答:作答.
刚刚学完实际问题与二元一次方程组,小明在数学报上看见一道例题及解答过程,可是中间部分不知道被谁撕去了,他还想用这道例题考下同学,你能帮小明补上吗?
小刚和小红一起在水果店买水果,小刚买了3千香蕉,2千克苹果,共花了18元.
解:设1千克香蕉x元,1千克苹果y元,则
3x+2y=18
2x+3y=17
解之得 x=4
y=3
答:每千克香蕉4元,每千克苹果3元.
小刚和小红一起在水果店买水果,小刚买了3千克香蕉,2千克苹果,共花了18元,小红买了2千克香蕉,3千克苹果,共花了17元.问每千克香蕉、苹果各多少元?
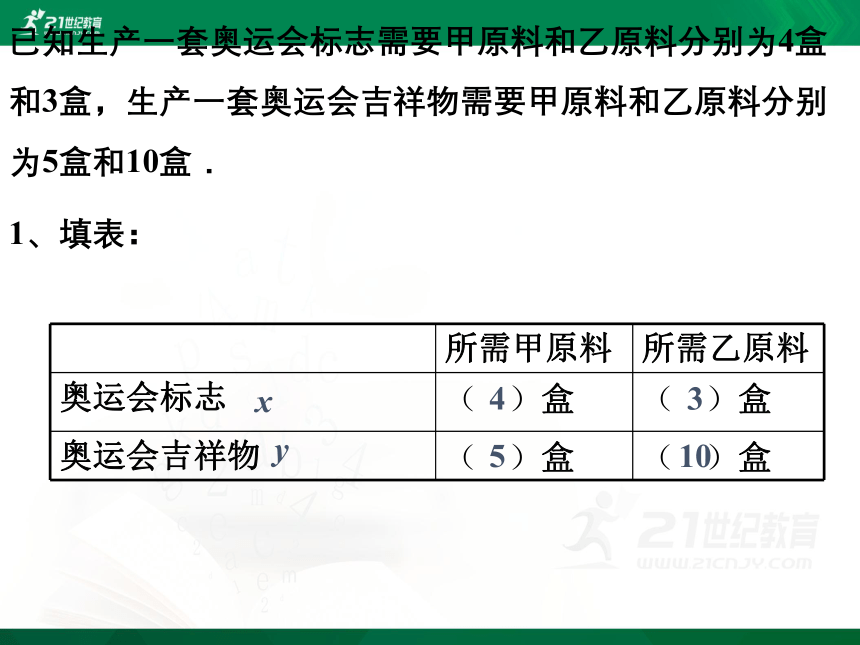
已知生产一套奥运会标志需要甲原料和乙原料分别为4盒和3盒,生产一套奥运会吉祥物需要甲原料和乙原料分别为5盒和10盒.
1、填表:
所需甲原料
所需乙原料
奥运会标志
( )盒
( )盒
奥运会吉祥物
( )盒
( )盒
4
5
3
10
x
y
2、生产1个奥运会标志和1个奥运会吉祥物需要甲原料和乙原料各多少?生产2个奥运会标志和3个奥运会吉祥物呢?生产x个奥运会标志和y个奥运会吉祥物呢?
3、该厂购进甲、乙原料的量分别为20000盒和30000盒,如果所进原料全部用完,求该厂能生产奥运会标志和奥运会吉祥物各多少套?
解:设生产奥运会标志x套,生产奥运会吉祥物y套.根据题意,得
?
í
ì
=
+
=
+
②
00
300
10
3
①
00
200
5
4
.
y
x
,
y
x
为迎接2008年奥运会,某工艺厂准备生产奥运会标志“中国印”和奥运会吉祥物“福娃”.该厂主要用甲、乙两种原料,已知生产一套奥运会标志需要甲原料和乙原料分别为4盒和3盒,生产一套奥运会吉祥物需要甲原料和乙原料分别为5盒和10盒.该厂购进甲、乙原料的量分别为20000盒和30000盒,如果所进原料全部用完,求该厂能生产奥运会标志和奥运会吉祥物各多少套?
所需甲原料
所需乙原料
奥运会标志
4盒
3盒
奥运会吉祥物
5盒
10盒
直击中考:
解:设生产奥运会标志x套,生产奥运会吉祥物y
套.根据题意,得
①×2-②得:5x=10000.
∴ x=2000.
把x=2000代入①得:5y=12000.
∴ y=2400.
答:该厂能生产奥运会标志2000套,生产奥运会吉祥
物2400套.
2分
6分
8分
感受中考:
步骤一定要规范呀!
=
+
=
+
②
00
300
10
3
①
00
200
5
4
.
y
x
,
y
x
1.某停车场的收费标准如下:中型汽车的停车费为6元/辆,小型汽车的停车费为4元/辆.现在停车场共有50辆中、小型汽车,这些车共缴纳停车费230元,中、小型汽车各有多少辆?
设中型车x辆,小型车y辆.
答:中型车15辆,小型车35辆.
由题意列出方程组:
解得:
设十位数为x,个位数为y.
由题意列出方程组:
2.一个两位数的十位数字与个位数字的和是7,如果把它的个位数字与十位数字对换,那么所得的两位数比原数大45.
求这个两位数.
解得:
答:这个两位数为16.
1.已知梯形的高是4cm,面积是18cm2,梯形的上底比下底的 要多1cm.求梯形上、下底的长度.
4cm
x
设上底xcm,下底ycm.由题意列出方程组:
答:上底3cm,下底6cm.
解得:
2.甲、乙两人沿400m的环形跑道同时同地出发跑步.如果同向而行,那么经过200s两人相遇;如果背向而行,那么经过40s两人相遇.求甲、乙两人的跑步速度.
400m
设甲、乙两人的跑步速度分别为xm/s和ym/s.由题意列出方程组:
答:甲、乙两人的跑步速度分别为6m/s和4m/s.
解得:
火车车皮
汽车
总物资
第一批物资
第二批物资
6x
15y
360
8x
10y
440
设火车车皮、汽车的装物资分别为xt,yt,填写下表并求x、y的值.
1.运输两批救灾物资,第一批360t,用6节火车车皮和15辆汽车正好装完;第二批440t,用8节火车车皮和10辆汽车正好装完.每节火车车皮和每辆汽车平均各装物资多少(单位:t)?
6x+15y=360,
8x+10y=440.
{
根据表格,可以列出方程组
解得 x=50,y=4.
答:火车车皮、汽车的装物资分别为50t,4t.
邮购册数
l~99
100以上
邮寄费用
书价优惠
书价的10%
免费邮寄
不优惠
优惠10%
2.邮购每册1.8元的某种杂志,邮寄费和优惠率如下表:
两次邮购这种杂志共200册,总计金额342元.两次邮购杂志各多少册?
x+y=200,
1.8(1+10%)x+1.8(1-10%)y=342.
{
根据表格,可以列出方程组
解得 x=50,y=150.
答:两次邮购杂志分别为50册,150册.
设两次邮购杂志分别为x册,y册.
本节你在知识上和数学思想等方面上有什么收获?
1、列二元一次方程组解决实际问题的步骤;审设列解验答.
2、转化的数学思想:把实际问题转化为解方程组的问题.把方程组转化为实际问题.
3、了解了我国古代数学的辉煌成就,从而努力学习,做好祖国的建设者和接班人!
小结:
1、我国古代数学名著《孙子算经》上有这样一道题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
解:设笼里有x只鸡,y只兔.
根据题意可列方程组得: .
达标测试:
谢谢聆听
10.5 用二元一次方程组解决问题
第10章 二元一次方程
2020-2021学年度苏科版七年级下册
养牛场原有30只大牛和15只小牛,一天约用饲料675㎏;一周后又购进12只大牛和5只小牛,这时1天约用饲料940㎏.饲养员李大叔估计每只大牛1天约需饲料18~20㎏,每只小牛1天约需饲料7~8㎏.你能否通过计算检验他的估计?
探究1
1、把探究1中表示等量关系的语句画记在课本上,并用等式表示这两个等量关系 .
2、若设每只大牛和每只小牛1天各约用x㎏和y㎏,依据上面等量关系列出方程组,并填在课本上.
3、解二元一次方程组有哪些方法?解所列的方程组有什么技巧?请总结,在练习本上写出解题过程.
4、如何判定饲养员李大叔的估计是否正确?
5、以上问题还能列出不同的二元一次方程组吗?结果是否一致?试一试!
1、把探究1中表示等量关系的语句画记在课本上,并用等式表示这两个等量关系
2、若设每只大牛和每只小牛1天各约用饲料x㎏和y㎏,依据上面等量关系列出方程组,并填在课本上.
(1)30只大牛所用饲料+15只小牛所用饲料=675㎏
(2)42只大牛所用饲料+20只小牛所用饲料=940㎏
30x+15y=675
42x+20y=940
3、解二元一次方程组有哪些方法?解所列的方程
组有什么技巧?请总结,在练习本上写出解题过程.
(1)代入法 (2)加减法
4、如何判定饲养员李大叔的估计是否正确?这就是说,每只大牛1天约需饲料20kg,每只小牛1天约需饲料5kg,因此,饲料李大叔对大牛的食量估计较准确,对小牛的食量估计偏高.
5、以上问题还能列出不同的二元一次方 程组吗?结果是否一致?试一试!
30x+15y=675
12x+5y=265
你知道吗?
列二元一次方程组解决实际问题的步骤:
审:读懂题意,找出题中的两个相等关系;
设:根据题意设上未知数;
列:根据相等关系列方程组;
解:解方程组;
验:检验1、解是否正确,2、解是否符合实
际意义;
答:作答.
刚刚学完实际问题与二元一次方程组,小明在数学报上看见一道例题及解答过程,可是中间部分不知道被谁撕去了,他还想用这道例题考下同学,你能帮小明补上吗?
小刚和小红一起在水果店买水果,小刚买了3千香蕉,2千克苹果,共花了18元.
解:设1千克香蕉x元,1千克苹果y元,则
3x+2y=18
2x+3y=17
解之得 x=4
y=3
答:每千克香蕉4元,每千克苹果3元.
小刚和小红一起在水果店买水果,小刚买了3千克香蕉,2千克苹果,共花了18元,小红买了2千克香蕉,3千克苹果,共花了17元.问每千克香蕉、苹果各多少元?
已知生产一套奥运会标志需要甲原料和乙原料分别为4盒和3盒,生产一套奥运会吉祥物需要甲原料和乙原料分别为5盒和10盒.
1、填表:
所需甲原料
所需乙原料
奥运会标志
( )盒
( )盒
奥运会吉祥物
( )盒
( )盒
4
5
3
10
x
y
2、生产1个奥运会标志和1个奥运会吉祥物需要甲原料和乙原料各多少?生产2个奥运会标志和3个奥运会吉祥物呢?生产x个奥运会标志和y个奥运会吉祥物呢?
3、该厂购进甲、乙原料的量分别为20000盒和30000盒,如果所进原料全部用完,求该厂能生产奥运会标志和奥运会吉祥物各多少套?
解:设生产奥运会标志x套,生产奥运会吉祥物y套.根据题意,得
?
í
ì
=
+
=
+
②
00
300
10
3
①
00
200
5
4
.
y
x
,
y
x
为迎接2008年奥运会,某工艺厂准备生产奥运会标志“中国印”和奥运会吉祥物“福娃”.该厂主要用甲、乙两种原料,已知生产一套奥运会标志需要甲原料和乙原料分别为4盒和3盒,生产一套奥运会吉祥物需要甲原料和乙原料分别为5盒和10盒.该厂购进甲、乙原料的量分别为20000盒和30000盒,如果所进原料全部用完,求该厂能生产奥运会标志和奥运会吉祥物各多少套?
所需甲原料
所需乙原料
奥运会标志
4盒
3盒
奥运会吉祥物
5盒
10盒
直击中考:
解:设生产奥运会标志x套,生产奥运会吉祥物y
套.根据题意,得
①×2-②得:5x=10000.
∴ x=2000.
把x=2000代入①得:5y=12000.
∴ y=2400.
答:该厂能生产奥运会标志2000套,生产奥运会吉祥
物2400套.
2分
6分
8分
感受中考:
步骤一定要规范呀!
=
+
=
+
②
00
300
10
3
①
00
200
5
4
.
y
x
,
y
x
1.某停车场的收费标准如下:中型汽车的停车费为6元/辆,小型汽车的停车费为4元/辆.现在停车场共有50辆中、小型汽车,这些车共缴纳停车费230元,中、小型汽车各有多少辆?
设中型车x辆,小型车y辆.
答:中型车15辆,小型车35辆.
由题意列出方程组:
解得:
设十位数为x,个位数为y.
由题意列出方程组:
2.一个两位数的十位数字与个位数字的和是7,如果把它的个位数字与十位数字对换,那么所得的两位数比原数大45.
求这个两位数.
解得:
答:这个两位数为16.
1.已知梯形的高是4cm,面积是18cm2,梯形的上底比下底的 要多1cm.求梯形上、下底的长度.
4cm
x
设上底xcm,下底ycm.由题意列出方程组:
答:上底3cm,下底6cm.
解得:
2.甲、乙两人沿400m的环形跑道同时同地出发跑步.如果同向而行,那么经过200s两人相遇;如果背向而行,那么经过40s两人相遇.求甲、乙两人的跑步速度.
400m
设甲、乙两人的跑步速度分别为xm/s和ym/s.由题意列出方程组:
答:甲、乙两人的跑步速度分别为6m/s和4m/s.
解得:
火车车皮
汽车
总物资
第一批物资
第二批物资
6x
15y
360
8x
10y
440
设火车车皮、汽车的装物资分别为xt,yt,填写下表并求x、y的值.
1.运输两批救灾物资,第一批360t,用6节火车车皮和15辆汽车正好装完;第二批440t,用8节火车车皮和10辆汽车正好装完.每节火车车皮和每辆汽车平均各装物资多少(单位:t)?
6x+15y=360,
8x+10y=440.
{
根据表格,可以列出方程组
解得 x=50,y=4.
答:火车车皮、汽车的装物资分别为50t,4t.
邮购册数
l~99
100以上
邮寄费用
书价优惠
书价的10%
免费邮寄
不优惠
优惠10%
2.邮购每册1.8元的某种杂志,邮寄费和优惠率如下表:
两次邮购这种杂志共200册,总计金额342元.两次邮购杂志各多少册?
x+y=200,
1.8(1+10%)x+1.8(1-10%)y=342.
{
根据表格,可以列出方程组
解得 x=50,y=150.
答:两次邮购杂志分别为50册,150册.
设两次邮购杂志分别为x册,y册.
本节你在知识上和数学思想等方面上有什么收获?
1、列二元一次方程组解决实际问题的步骤;审设列解验答.
2、转化的数学思想:把实际问题转化为解方程组的问题.把方程组转化为实际问题.
3、了解了我国古代数学的辉煌成就,从而努力学习,做好祖国的建设者和接班人!
小结:
1、我国古代数学名著《孙子算经》上有这样一道题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
解:设笼里有x只鸡,y只兔.
根据题意可列方程组得: .
达标测试:
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
