11.1 生活中的不等式(第1课时) 课件(共25张PPT)
文档属性
| 名称 | 11.1 生活中的不等式(第1课时) 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 17:38:51 | ||
图片预览








文档简介
11.1 生活中的不等式
第11章 不等式
第1课时
2020-2021学年度苏科版七年级下册
生活中的不等式
小磊和他的妈妈、爸爸的体重分别为30kg、55kg和75kg.春节期间,去公园游乐场玩跷跷板,
请你当裁判
你能知道游戏的结果吗?为什么?
因为30<55,所以小磊会向上跷;
因为30+55>75,所以爸爸会向上跷.
若小磊和妈妈坐一头,爸爸坐在另一头时,
谁会向上跷?
小磊和妈妈玩时,谁会向上跷?
“不大于” 指的是 “ ”,
通常用符号 “ ” 表示.
类似地,“不小于”指的是“大于或等于” .
通常用符号“≥”表示.(读作:“大于或等于”).
小于或等于
≤
不等关系符号
例如,x 不大于10 可以表示为
x≤10(读作:“x小于或等于10”) .
(1)(图中的交通图标表示该公路某路段上汽车的最高时速不得超过100km.如果一辆汽车的行驶速度是akm/h,那么a与100之间的关系表示为
你会用式子表示下面的数量关系吗?
a 100
≤
≤
(2)下图为公路上对汽车的限速标志,表示汽车在该路段行使的速度不得超过40Km/h,用v(km/h)表示汽车的速度,怎样表示v和40之间的关系?
你会用式子表示下面的数量关系吗?
V 40
≤
≤
(3)根据科学家测定,太阳表面的温度不低于6000℃.设太阳表面的温度为t(℃),怎样表示t和6000之间的关系?
t 6000
≥
≥
你会用式子表示下面的数量关系吗?
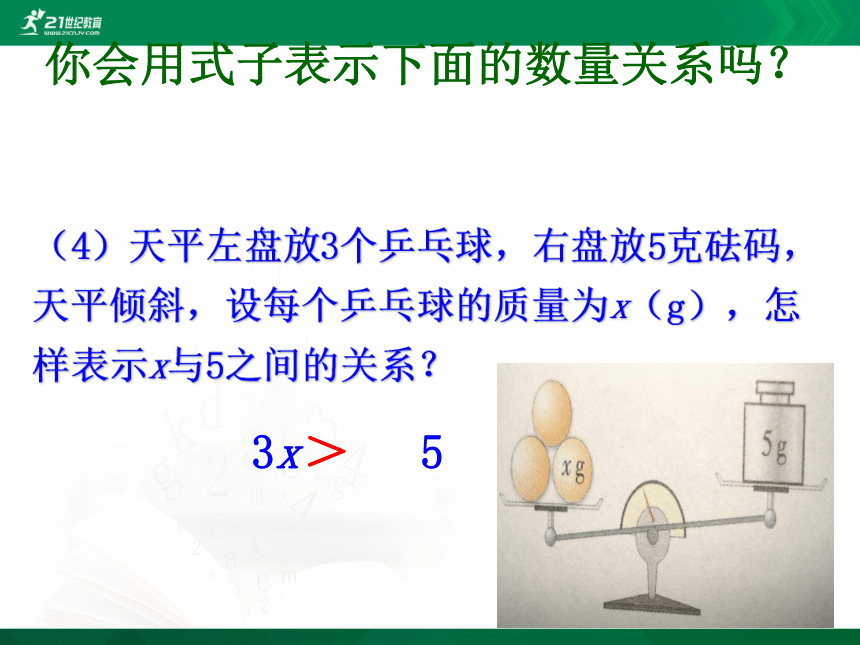
(4)天平左盘放3个乒乓球,右盘放5克砝码,天平倾斜,设每个乒乓球的质量为x(g),怎样表示x与5之间的关系?
3x 5
>
>
你会用式子表示下面的数量关系吗?
(5)小明与小聪玩跷跷板,大家都不用力时,跷跷板左低右高.小明的身体质量为p(kg),小聪的身体质量为q(kg),书包的质量为2kg,怎样表示p 、q之间的关系?
p q +2
<
<
你会用式子表示下面的数量关系吗?
(6)要使代数式 有意义,x的值与3之间有什么关系?
x 3
≠
≠
你会用式子表示下面的数量关系吗?
(x-3)0
用适当的符号表示下列关系:
(1)直角三角形斜边比它的两直角边a 、b都长.
(2) x与17的和比它的5倍小.
(3) x的3倍与8的和比x的5倍大.
(4) 地球上海洋面积s1大于陆地面积s2.
(5) 铅球的质量m1比篮球的质量m2大.
c>a
c>b
3x+8>5x
s1>s2
m1 > m2
x+17<5x
你一定能行的!
观察如下关系式,它们有什么共同特点?
(1)
(2)
(3)
(4)
一般地,用符号“<”(或“≤”),“>”
(或“≥”)连接的式子叫做不等式.
不 等 式 的 定 义
≤ 25
≥100
<
5+3x>240
判断下列各式中哪些是不等式?
(1) a2+1>0 (2) a+b=0
(3) 8<9 (4) 3x-1≤x
(5) 4-2x (6) x-y≠1
认一认
不是
不是
是
是
是
是
(2)y不小于1与y的差;
(3)a的2倍比a的平方的相反数小.
1、根据下列数量关系列出不等式:
2x+1>x
2a < -a2
y ≥ 1-y
(1)x的2倍与1的和大于x ;
列不等式时先抓住关键词,
再选准不等号.
答一答
关键
词语
不等号
第一类——明显的不等关系
比…大
大于
>
小于
<
≤
至多
不大于
不超过
≥
不小于
不低于
至少
超过
低于
比…小
注意“不”字哦!
≠
大于或
小于
2、用不等式表示下列关系:
a>0
|y|-8< 0
(a-b)2≥0
(1)a是正数;
(2)y的绝对值与-8的和为负数 ;
(3)a与b的差的平方是非负数;
①抓住关键词
②选准不等号
第二类——隐含的不等关系
正数
负数
非负数
非正数
>0
<0
≥0
≤0
通过测量一棵树的树围(树干的周长)可以计算出它的树龄,通常规定以树干离地面1.5cm的地方作为测量部位. 某树栽种时的树围为5cm,以后树围每年增加约3cm .这棵树至少生长多少年其树围才能超过 2.4 m?
解:设这棵树生长x年其树围才能超过2.4m,
依题意得:
5+3x>240
做 一 做
A
a
0
1、如图,数轴上A,B两点对应的分数分别为a,b,则a与b的大小关系是 .(用不等式表示)
1
2
3
4
b
B
(第1题)
2、用不等式表示:
(1)a是负数.
(2)x比-1大.
(3)m与n的差不大于2.
(4)x与-5的差是正数.
a<0
x>-1
m-n ≤ 2
x-(-5) >0
a < b
3、用不等式表示下列关系:
(1)x的一半不大于-2;
(2)y与3的差大于0.5 ;
(3)a是负数;
(4)b是非负数.
解:
(1)0.5x≤-2,
(2)y-3>0.5,
(3)a<0.
(4)b是非负数,就是b不是负数,它可以是正数或零,即b>0或b=0,通常可以表示成b≥ 0.
(用不等式表示不等关系是研究不等式的基础,在表示时一定要抓住关键词语,弄清不等关系.)
1.(口答)用不等式表示:
(1)a是负数;
(2)x与5的和大于2;
(3)x与a的差小于2;
(4)x与y的差是非负数.
(1)a<0;
(2)x+5>2;
(3)x-a<2;
(4)x-y≥0.
1.试举几个用不等式表示的例子.
(1)x的3倍与8的和比x的5倍小;
(2)x是非负数;
(3)老师的年龄不超过你的年龄的2倍。
(1)3x+8<5x;
(2)x≥0;
(3)设老师的年龄为x,你的年龄为y,则x≤2y.
2.用适当的不等号表示下列关系:
(1)a是非负数;
(2)直角三角形的一条直角边a比斜边c短;
(3)x与17的和比它的5倍小;
(4)两数的平方和不小于这两数积的2倍.
a≥0.
A<c.
x+17<5x.
设两数分别为x、y.x2+y2≥2xy.
2.根据下列含有“最”字的实例,写出不等式:
(1)火车提速后,速度(ν)最高可达350km/h;
(2)某班学生的身高(h)最高为1.74m;
(3)某班学生从家到校的路程(s)最近是1km.
(1) ν≤350;
(2)h≤1.74;
(3)s≥1.
谢谢聆听
第11章 不等式
第1课时
2020-2021学年度苏科版七年级下册
生活中的不等式
小磊和他的妈妈、爸爸的体重分别为30kg、55kg和75kg.春节期间,去公园游乐场玩跷跷板,
请你当裁判
你能知道游戏的结果吗?为什么?
因为30<55,所以小磊会向上跷;
因为30+55>75,所以爸爸会向上跷.
若小磊和妈妈坐一头,爸爸坐在另一头时,
谁会向上跷?
小磊和妈妈玩时,谁会向上跷?
“不大于” 指的是 “ ”,
通常用符号 “ ” 表示.
类似地,“不小于”指的是“大于或等于” .
通常用符号“≥”表示.(读作:“大于或等于”).
小于或等于
≤
不等关系符号
例如,x 不大于10 可以表示为
x≤10(读作:“x小于或等于10”) .
(1)(图中的交通图标表示该公路某路段上汽车的最高时速不得超过100km.如果一辆汽车的行驶速度是akm/h,那么a与100之间的关系表示为
你会用式子表示下面的数量关系吗?
a 100
≤
≤
(2)下图为公路上对汽车的限速标志,表示汽车在该路段行使的速度不得超过40Km/h,用v(km/h)表示汽车的速度,怎样表示v和40之间的关系?
你会用式子表示下面的数量关系吗?
V 40
≤
≤
(3)根据科学家测定,太阳表面的温度不低于6000℃.设太阳表面的温度为t(℃),怎样表示t和6000之间的关系?
t 6000
≥
≥
你会用式子表示下面的数量关系吗?
(4)天平左盘放3个乒乓球,右盘放5克砝码,天平倾斜,设每个乒乓球的质量为x(g),怎样表示x与5之间的关系?
3x 5
>
>
你会用式子表示下面的数量关系吗?
(5)小明与小聪玩跷跷板,大家都不用力时,跷跷板左低右高.小明的身体质量为p(kg),小聪的身体质量为q(kg),书包的质量为2kg,怎样表示p 、q之间的关系?
p q +2
<
<
你会用式子表示下面的数量关系吗?
(6)要使代数式 有意义,x的值与3之间有什么关系?
x 3
≠
≠
你会用式子表示下面的数量关系吗?
(x-3)0
用适当的符号表示下列关系:
(1)直角三角形斜边比它的两直角边a 、b都长.
(2) x与17的和比它的5倍小.
(3) x的3倍与8的和比x的5倍大.
(4) 地球上海洋面积s1大于陆地面积s2.
(5) 铅球的质量m1比篮球的质量m2大.
c>a
c>b
3x+8>5x
s1>s2
m1 > m2
x+17<5x
你一定能行的!
观察如下关系式,它们有什么共同特点?
(1)
(2)
(3)
(4)
一般地,用符号“<”(或“≤”),“>”
(或“≥”)连接的式子叫做不等式.
不 等 式 的 定 义
≤ 25
≥100
<
5+3x>240
判断下列各式中哪些是不等式?
(1) a2+1>0 (2) a+b=0
(3) 8<9 (4) 3x-1≤x
(5) 4-2x (6) x-y≠1
认一认
不是
不是
是
是
是
是
(2)y不小于1与y的差;
(3)a的2倍比a的平方的相反数小.
1、根据下列数量关系列出不等式:
2x+1>x
2a < -a2
y ≥ 1-y
(1)x的2倍与1的和大于x ;
列不等式时先抓住关键词,
再选准不等号.
答一答
关键
词语
不等号
第一类——明显的不等关系
比…大
大于
>
小于
<
≤
至多
不大于
不超过
≥
不小于
不低于
至少
超过
低于
比…小
注意“不”字哦!
≠
大于或
小于
2、用不等式表示下列关系:
a>0
|y|-8< 0
(a-b)2≥0
(1)a是正数;
(2)y的绝对值与-8的和为负数 ;
(3)a与b的差的平方是非负数;
①抓住关键词
②选准不等号
第二类——隐含的不等关系
正数
负数
非负数
非正数
>0
<0
≥0
≤0
通过测量一棵树的树围(树干的周长)可以计算出它的树龄,通常规定以树干离地面1.5cm的地方作为测量部位. 某树栽种时的树围为5cm,以后树围每年增加约3cm .这棵树至少生长多少年其树围才能超过 2.4 m?
解:设这棵树生长x年其树围才能超过2.4m,
依题意得:
5+3x>240
做 一 做
A
a
0
1、如图,数轴上A,B两点对应的分数分别为a,b,则a与b的大小关系是 .(用不等式表示)
1
2
3
4
b
B
(第1题)
2、用不等式表示:
(1)a是负数.
(2)x比-1大.
(3)m与n的差不大于2.
(4)x与-5的差是正数.
a<0
x>-1
m-n ≤ 2
x-(-5) >0
a < b
3、用不等式表示下列关系:
(1)x的一半不大于-2;
(2)y与3的差大于0.5 ;
(3)a是负数;
(4)b是非负数.
解:
(1)0.5x≤-2,
(2)y-3>0.5,
(3)a<0.
(4)b是非负数,就是b不是负数,它可以是正数或零,即b>0或b=0,通常可以表示成b≥ 0.
(用不等式表示不等关系是研究不等式的基础,在表示时一定要抓住关键词语,弄清不等关系.)
1.(口答)用不等式表示:
(1)a是负数;
(2)x与5的和大于2;
(3)x与a的差小于2;
(4)x与y的差是非负数.
(1)a<0;
(2)x+5>2;
(3)x-a<2;
(4)x-y≥0.
1.试举几个用不等式表示的例子.
(1)x的3倍与8的和比x的5倍小;
(2)x是非负数;
(3)老师的年龄不超过你的年龄的2倍。
(1)3x+8<5x;
(2)x≥0;
(3)设老师的年龄为x,你的年龄为y,则x≤2y.
2.用适当的不等号表示下列关系:
(1)a是非负数;
(2)直角三角形的一条直角边a比斜边c短;
(3)x与17的和比它的5倍小;
(4)两数的平方和不小于这两数积的2倍.
a≥0.
A<c.
x+17<5x.
设两数分别为x、y.x2+y2≥2xy.
2.根据下列含有“最”字的实例,写出不等式:
(1)火车提速后,速度(ν)最高可达350km/h;
(2)某班学生的身高(h)最高为1.74m;
(3)某班学生从家到校的路程(s)最近是1km.
(1) ν≤350;
(2)h≤1.74;
(3)s≥1.
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
