安徽省亳州蒙城县第六中学2020-2021学年九年级下学期开学测试数学试卷(Word版 无答案)
文档属性
| 名称 | 安徽省亳州蒙城县第六中学2020-2021学年九年级下学期开学测试数学试卷(Word版 无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 393.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 00:00:00 | ||
图片预览

文档简介
2021年春季开学九年级第一次测试
数学试卷
(试卷满分为150分,考试时间为120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A,B,C,D四个选项,其中只有一个是符合题目要求的.
1.实数2,0,-1,中,为负数的是(
)
A.
B.
C.
-1
D.
2.计算的结果是(
)
A.-
B.
C.
D.
3.如图所示的几何体是由四个大小相同的小立方块搭成,其左视图是(
)
4.2020年一来,安徽开展“抗疫情、补短板、促攻坚”专项行动,其中帮销扶贫产品209.6亿元。209.6亿元用科学记数法表示为多少元(
)
A.2.096×1011
B.0.2096×1010
C.2.096×103
D.2.096×1010
5..不等式的解集在数轴上表示正确的是(
)
A.
B.
C.
D.
6.已知反比例函数的图象经过点(2,﹣4),那么这个反比例函数的解析式是( )
A.y=
B.y=﹣
C.y=
D.y=﹣
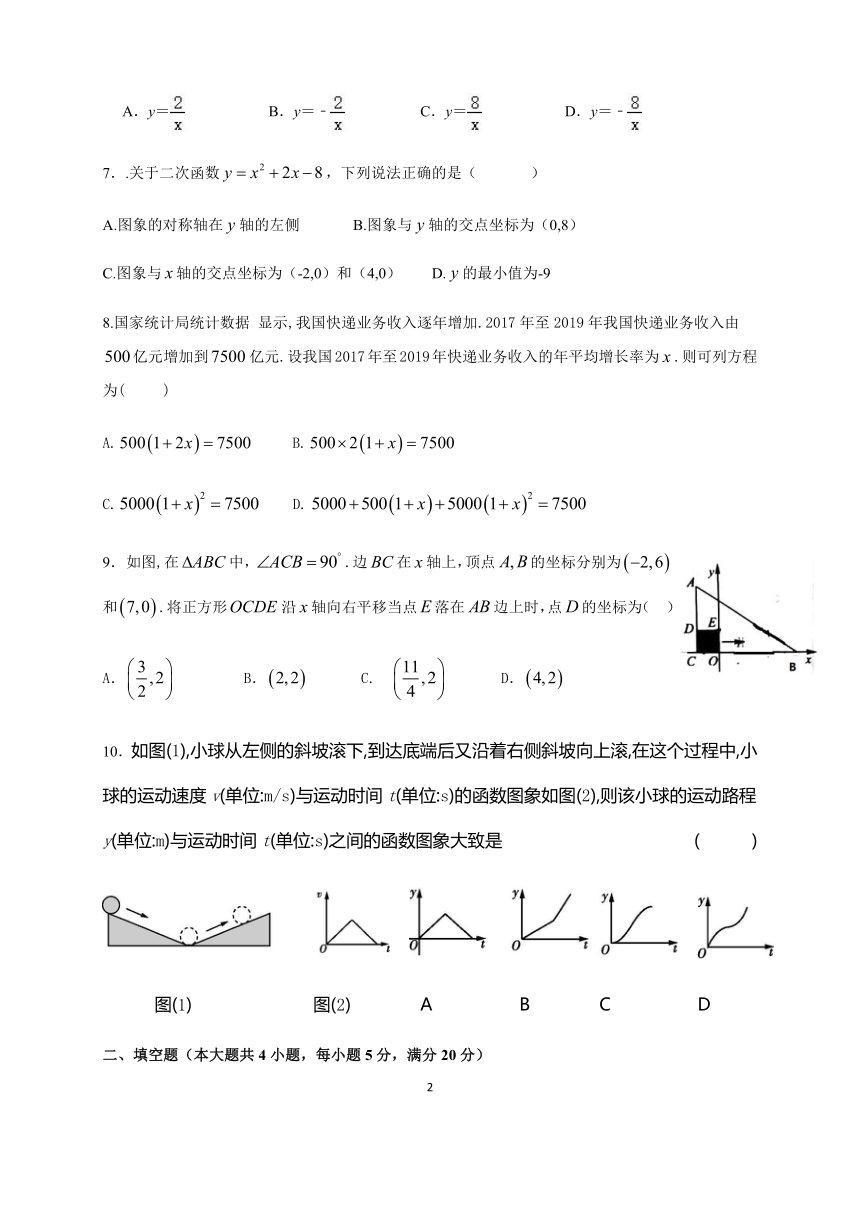
7..关于二次函数,下列说法正确的是(
)
A.图象的对称轴在轴的左侧
B.图象与轴的交点坐标为(0,8)
C.图象与轴的交点坐标为(-2,0)和(4,0)
D.的最小值为-9
8.国家统计局统计数据
显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由亿元增加到亿元.设我国2017年至2019年快递业务收入的年平均增长率为.则可列方程为(
)
A.
B.
C.
D.
9.
如图,在中,.边在轴上,顶点的坐标分别为和.将正方形沿轴向右平移当点落在边上时,点的坐标为(
)
A.
B.
C.
D.
10.如图(1),小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度v(单位:m/s)与运动时间t(单位:s)的函数图象如图(2),则该小球的运动路程y(单位:m)与运动时间t(单位:s)之间的函数图象大致是
(
)
图(1) 图(2)
A
B
C
D
二、填空题(本大题共4小题,每小题5分,满分20分)
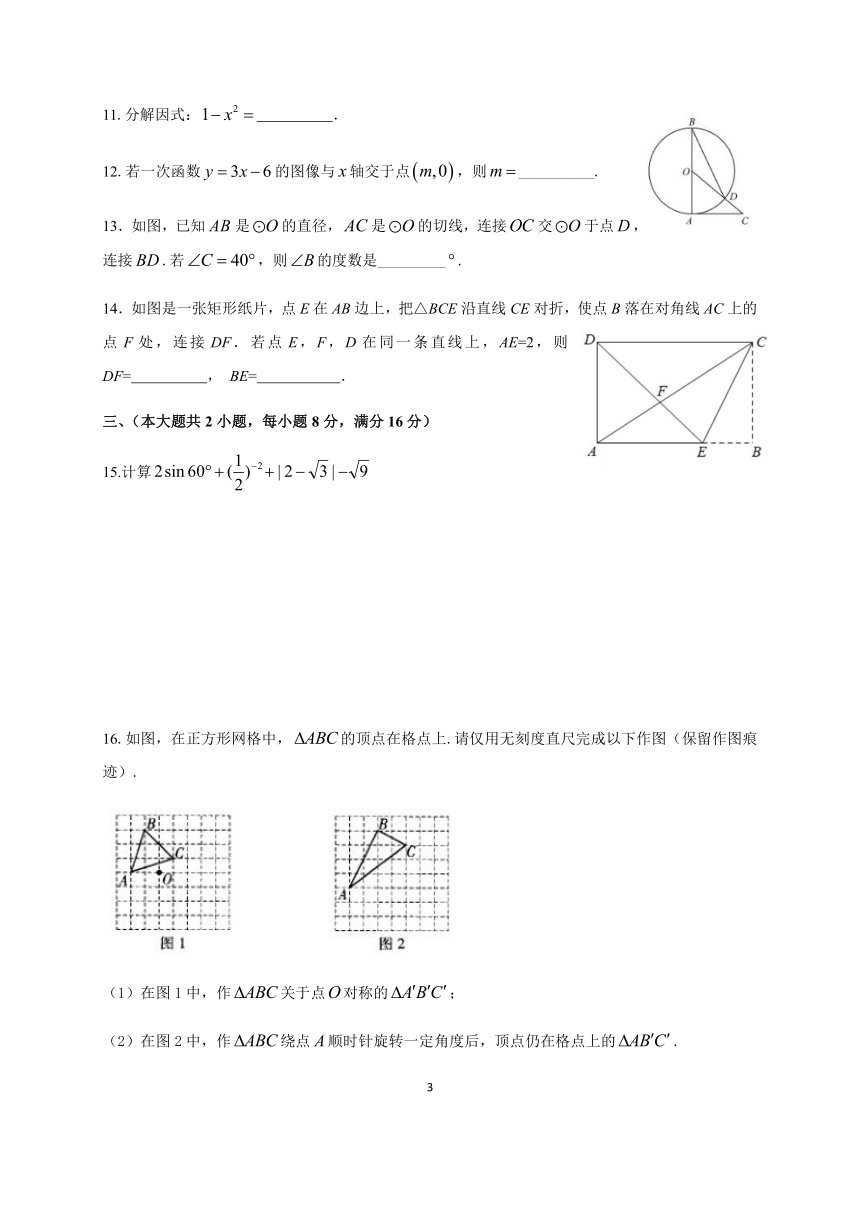
11.分解因式:
.
12.若一次函数的图像与轴交于点,则__________.
13.如图,已知是的直径,是的切线,连接交于点,连接.若,则的度数是_________.
14.如图是一张矩形纸片,点E在AB边上,把△BCE沿直线CE对折,使点B落在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上,AE=2,则DF=
,
BE=
.
三、(本大题共2小题,每小题8分,满分16分)
15.计算
16.如图,在正方形网格中,的顶点在格点上.请仅用无刻度直尺完成以下作图(保留作图痕迹).
(1)在图1中,作关于点对称的;
(2)在图2中,作绕点顺时针旋转一定角度后,顶点仍在格点上的.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在矩形中,是的中点,,垂足为.
(1)求证:;
(2)若,,求的长.
18.为了建设水墨丹青新蒙城,推进城区污水系统综合治理项目,需要从如图,两地向地新建,两条笔直的污水收集管道,现测得地在地北偏东方向上,在地北偏西方向上,的距离为,求新建管道的总长度.(结果精确到,,,,)
五、(本大题共2小题,每小题10分,满分20分)
19.如图,中,,顶点都在反比例函数的图象上,直线轴,垂足为,连结,,并延长交于点,当时,点恰为的中点,若,.
(1)求反比例函数的解析式;
(2)求的度数.
20.已知:如图,是的直径,点为上一点,点是上一点,连接并延长至点,使,与交于点.
(1)求证:是的切线;
(2)若平分,求证:.
六、(本题满分12分)
21.某单位食堂为全体960名职工提供了A,B,C,D四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取240名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
(1)在抽取的240人中最喜欢A套餐的人数为
,扇形统计图中“C”对应扇形的圆心角的大小为
°;
(2)依据本次调查的结果,估计全体960名职工中最喜欢B套餐的人数;
(3)现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
七、(本题满分12分)
22.在平面直角坐标系中,设二次函数y1=x2+bx+a,y2=ax2+bx+1(a,b是实数,a≠0)
(1)若函数y1的对称轴为直线x=3,且函数y1的图象经过点(a,b),求函数y1的表达式.
(2)若函数y1的图象经过点(r,0),其中r≠0,求证:函数y2的图象经过点(,0).
(3)设函数y1和函数y2的最小值分别为m和n,若m+n=0,求m,n的值.
八、(本题满分14分)
23.如图(1),在△ABC中,AB=AC,BC=6,BE为中线,点D为BC边上一点,BD=2CD,DF⊥BE于点F,EH⊥BC于点H.
(1)CH的长为 ;?
(2)求BF·BE的值;
(3)如图(2),连接FC,求证:∠EFC=∠ABC.
18
数学试卷
(试卷满分为150分,考试时间为120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A,B,C,D四个选项,其中只有一个是符合题目要求的.
1.实数2,0,-1,中,为负数的是(
)
A.
B.
C.
-1
D.
2.计算的结果是(
)
A.-
B.
C.
D.
3.如图所示的几何体是由四个大小相同的小立方块搭成,其左视图是(
)
4.2020年一来,安徽开展“抗疫情、补短板、促攻坚”专项行动,其中帮销扶贫产品209.6亿元。209.6亿元用科学记数法表示为多少元(
)
A.2.096×1011
B.0.2096×1010
C.2.096×103
D.2.096×1010
5..不等式的解集在数轴上表示正确的是(
)
A.
B.
C.
D.
6.已知反比例函数的图象经过点(2,﹣4),那么这个反比例函数的解析式是( )
A.y=
B.y=﹣
C.y=
D.y=﹣
7..关于二次函数,下列说法正确的是(
)
A.图象的对称轴在轴的左侧
B.图象与轴的交点坐标为(0,8)
C.图象与轴的交点坐标为(-2,0)和(4,0)
D.的最小值为-9
8.国家统计局统计数据
显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由亿元增加到亿元.设我国2017年至2019年快递业务收入的年平均增长率为.则可列方程为(
)
A.
B.
C.
D.
9.
如图,在中,.边在轴上,顶点的坐标分别为和.将正方形沿轴向右平移当点落在边上时,点的坐标为(
)
A.
B.
C.
D.
10.如图(1),小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度v(单位:m/s)与运动时间t(单位:s)的函数图象如图(2),则该小球的运动路程y(单位:m)与运动时间t(单位:s)之间的函数图象大致是
(
)
图(1) 图(2)
A
B
C
D
二、填空题(本大题共4小题,每小题5分,满分20分)
11.分解因式:
.
12.若一次函数的图像与轴交于点,则__________.
13.如图,已知是的直径,是的切线,连接交于点,连接.若,则的度数是_________.
14.如图是一张矩形纸片,点E在AB边上,把△BCE沿直线CE对折,使点B落在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上,AE=2,则DF=
,
BE=
.
三、(本大题共2小题,每小题8分,满分16分)
15.计算
16.如图,在正方形网格中,的顶点在格点上.请仅用无刻度直尺完成以下作图(保留作图痕迹).
(1)在图1中,作关于点对称的;
(2)在图2中,作绕点顺时针旋转一定角度后,顶点仍在格点上的.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在矩形中,是的中点,,垂足为.
(1)求证:;
(2)若,,求的长.
18.为了建设水墨丹青新蒙城,推进城区污水系统综合治理项目,需要从如图,两地向地新建,两条笔直的污水收集管道,现测得地在地北偏东方向上,在地北偏西方向上,的距离为,求新建管道的总长度.(结果精确到,,,,)
五、(本大题共2小题,每小题10分,满分20分)
19.如图,中,,顶点都在反比例函数的图象上,直线轴,垂足为,连结,,并延长交于点,当时,点恰为的中点,若,.
(1)求反比例函数的解析式;
(2)求的度数.
20.已知:如图,是的直径,点为上一点,点是上一点,连接并延长至点,使,与交于点.
(1)求证:是的切线;
(2)若平分,求证:.
六、(本题满分12分)
21.某单位食堂为全体960名职工提供了A,B,C,D四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取240名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
(1)在抽取的240人中最喜欢A套餐的人数为
,扇形统计图中“C”对应扇形的圆心角的大小为
°;
(2)依据本次调查的结果,估计全体960名职工中最喜欢B套餐的人数;
(3)现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
七、(本题满分12分)
22.在平面直角坐标系中,设二次函数y1=x2+bx+a,y2=ax2+bx+1(a,b是实数,a≠0)
(1)若函数y1的对称轴为直线x=3,且函数y1的图象经过点(a,b),求函数y1的表达式.
(2)若函数y1的图象经过点(r,0),其中r≠0,求证:函数y2的图象经过点(,0).
(3)设函数y1和函数y2的最小值分别为m和n,若m+n=0,求m,n的值.
八、(本题满分14分)
23.如图(1),在△ABC中,AB=AC,BC=6,BE为中线,点D为BC边上一点,BD=2CD,DF⊥BE于点F,EH⊥BC于点H.
(1)CH的长为 ;?
(2)求BF·BE的值;
(3)如图(2),连接FC,求证:∠EFC=∠ABC.
18
同课章节目录
