11.4 解一元一次不等式(第1课时) 课件(共26张PPT)
文档属性
| 名称 | 11.4 解一元一次不等式(第1课时) 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 18:04:49 | ||
图片预览








文档简介
11.4 解一元一次不等式
第1课时
第11章 不等式
2020-2021学年度苏科版七年级下册
一元一次不等式
什么是不等式?
什么是不等式的解集?
不等式解集的表示方法
一般地,用符号“<”(或“≤”), “>”(或“≥”)连接的式子叫做不等式.
一个含有未知数的不等式的所有解,组成这个不等式的解集.
1.最简不等式法; 2.用数轴来表示
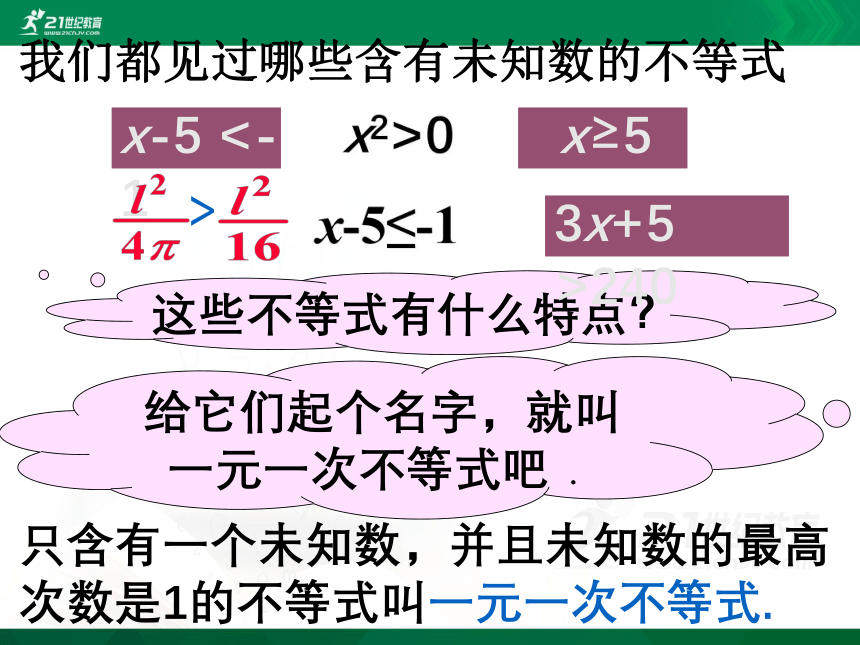
这些不等式有什么特点?
我们都见过哪些含有未知数的不等式
只含有一个未知数,并且未知数的最高次数是1的不等式叫一元一次不等式.
x-5 <-1
>
x-5≤-1
x2>0
3x+5 >240
x≥5
给它们起个名字,就叫一元一次不等式吧.
怎样求一元一次不等式3x+70>100的解集?
与解方程类似.运用不等式性质.将这个不等式变形.
根据不等式的性质1,不等式的两边都减去70,得
3x>l00-70.
合并同类项,得
3x>30.
议一议
这就是解不等式中的移项,与解方程中的移项类似.
这个不等式的解集在数轴上表示如下(图11-5):
根据不等式的性质2,不等式的两边都除以3,得
x>10.
图11-5
解:移项,得
-2x>6-14.
合并同类项,得
-2x>-8.
根据不等式的性质2,不等式的两边两边都除以-2,得
x<4.
这个不等式的解集在数轴上表示如下(图11-6):
例1解不等式14-2x>6,并把它的解集在数轴上表示出来.
解:根据不等式的性质2,不等式的两边两边都乘2,得
2(2x-1) ≥3x-1.
去括号,得
4x-2 ≥3x-1.
移项,得
4x-3x ≥-1+2.
合并同类项,得 x≥1.
这个不等式的解集在数轴上表示如下(图11-7):
例2 解不等式2x-1≥ ,并把它的解集在数轴上表示出来.
解:去分母,得
6-3(x+6) <2(2x+1).
去括号,得
6-3x-18<4x+2.
移项、合并同类项,得
-7x<14.
两边都除以-7,得
x>-2.
这个不等式的解集在数轴上表示如下(图11-8):
例3 解不等式 ,并把它的解集在数轴上表示出来.
解下列不等式,并将解集在数轴上表示出来:
(1)2x-1<4x+13;
(2)2(5x+3)≤x-3(1-2x).
解 (1)2x-1<4x+13.
移项,得
2x-4x<13+1.
合并同类项,得
-2x<14.
两边都除以-2,得
x>-7.
它在数轴上的表示如图.
(2)2(5x+3)≤x-3(1-2x).
去括号,得
10x+6移项、合并同类项,得
3x≤-9.
两边都除以3,得
x≤-3.
它在数轴上的表示如图8.2.5.
哇!一元一次解不等式可以移项!
解不等式3-x<2x+6,并把它的解集表示在数轴上.
两边都加上x,得
解:
3-x+x<2x+6+x
合并同类项,得
3<3x+6
两边都加上-6,得
3-6<3x+6-6
两边都除以3,得-1x>-1 .
x>-1
3
4
2
5
6
7
1
0
-1
8
9
10
11
12
13
解不等式 ,并把它的解集表示在数轴上.
去分母,得
解:
3(x-2)≥2(7-x)
去括号,得
3x-6≥14-2x
移项合并同类项,得
两边都除以5,得 x≥4 .
5x≥20
x≥4
3
4
2
5
6
7
1
0
-1
8
9
10
11
12
13
一元一次不等式的解法
要特别注意它们不一样的地方!!!
一元一次不等式
最简不等式
不等式的基本性质
去分母
去括号
移项
合并同类项
系数化为1
步骤
性质2
性质1
性质2
没什么新鲜的,跟解一元一次方程差不多……
例 当x在什么范围内取值时,代数式 的值比x+1的值大?
去分母,得
解:根据题意,x应满足不等式
1+2x>3(x+1).
去括号,得
1+2x>3x+3.
移项,合并同类项,得
将未知数系数化为1,得
-x>2.
x<-2.
即当x<-2时,代数式 的值比x+1的值大.
例3 求不等式 的正整数解.
去分母,得
解:
3(x+1) ≥2(2x-1).
去括号,得
3x+3≥4x-2.
移项,合并同类项,得
将未知数系数化为1,得
-x≥-5.
x ≤ 5.
所以,满足这个不等式的正整数解为x=1,2,3,4,5.
解不等式,并把它的解集表示在数轴上.
做一做
一元一次不等式与一次函数
答案:
当x> 时,y1<y2;
当x= 时,y1=y2;
当x< 时,y1>y2.
例、若y1=-x+3,y2=3x-4,试确定当x取何值时
(1)y1<y2?
(2)y1=y2?
(3)y1>y2?
根据不等式的性质1,在不等式的两边都减去70,得
3x+70-70>100-70
合并同类项,得
3x>30
根据不等式的性质2,在不等式的两边都除以3,得
x>10
这个不等式的解集在数轴上表示如下:
0
10
其实这就是移项
计算:3x+70>100
解不等式,并在数轴上表示解集:
解:去分母,得 3(x-3)<2(2x-5),
去括号,得 3x-9<4x-10,
移项,得 3x-4x<-10+9,
合并同类项,得 -x<-1,
系数化为1,得 x>1 .
<
它在数轴上表示如下:
0
1
小结:
这堂课的目标是掌握一元一次不等式的解题步骤,并学会解一元一次不等式.
你达到目标了没有?谈谈你今天的收获.
谢谢聆听
第1课时
第11章 不等式
2020-2021学年度苏科版七年级下册
一元一次不等式
什么是不等式?
什么是不等式的解集?
不等式解集的表示方法
一般地,用符号“<”(或“≤”), “>”(或“≥”)连接的式子叫做不等式.
一个含有未知数的不等式的所有解,组成这个不等式的解集.
1.最简不等式法; 2.用数轴来表示
这些不等式有什么特点?
我们都见过哪些含有未知数的不等式
只含有一个未知数,并且未知数的最高次数是1的不等式叫一元一次不等式.
x-5 <-1
>
x-5≤-1
x2>0
3x+5 >240
x≥5
给它们起个名字,就叫一元一次不等式吧.
怎样求一元一次不等式3x+70>100的解集?
与解方程类似.运用不等式性质.将这个不等式变形.
根据不等式的性质1,不等式的两边都减去70,得
3x>l00-70.
合并同类项,得
3x>30.
议一议
这就是解不等式中的移项,与解方程中的移项类似.
这个不等式的解集在数轴上表示如下(图11-5):
根据不等式的性质2,不等式的两边都除以3,得
x>10.
图11-5
解:移项,得
-2x>6-14.
合并同类项,得
-2x>-8.
根据不等式的性质2,不等式的两边两边都除以-2,得
x<4.
这个不等式的解集在数轴上表示如下(图11-6):
例1解不等式14-2x>6,并把它的解集在数轴上表示出来.
解:根据不等式的性质2,不等式的两边两边都乘2,得
2(2x-1) ≥3x-1.
去括号,得
4x-2 ≥3x-1.
移项,得
4x-3x ≥-1+2.
合并同类项,得 x≥1.
这个不等式的解集在数轴上表示如下(图11-7):
例2 解不等式2x-1≥ ,并把它的解集在数轴上表示出来.
解:去分母,得
6-3(x+6) <2(2x+1).
去括号,得
6-3x-18<4x+2.
移项、合并同类项,得
-7x<14.
两边都除以-7,得
x>-2.
这个不等式的解集在数轴上表示如下(图11-8):
例3 解不等式 ,并把它的解集在数轴上表示出来.
解下列不等式,并将解集在数轴上表示出来:
(1)2x-1<4x+13;
(2)2(5x+3)≤x-3(1-2x).
解 (1)2x-1<4x+13.
移项,得
2x-4x<13+1.
合并同类项,得
-2x<14.
两边都除以-2,得
x>-7.
它在数轴上的表示如图.
(2)2(5x+3)≤x-3(1-2x).
去括号,得
10x+6
3x≤-9.
两边都除以3,得
x≤-3.
它在数轴上的表示如图8.2.5.
哇!一元一次解不等式可以移项!
解不等式3-x<2x+6,并把它的解集表示在数轴上.
两边都加上x,得
解:
3-x+x<2x+6+x
合并同类项,得
3<3x+6
两边都加上-6,得
3-6<3x+6-6
两边都除以3,得-1
x>-1
3
4
2
5
6
7
1
0
-1
8
9
10
11
12
13
解不等式 ,并把它的解集表示在数轴上.
去分母,得
解:
3(x-2)≥2(7-x)
去括号,得
3x-6≥14-2x
移项合并同类项,得
两边都除以5,得 x≥4 .
5x≥20
x≥4
3
4
2
5
6
7
1
0
-1
8
9
10
11
12
13
一元一次不等式的解法
要特别注意它们不一样的地方!!!
一元一次不等式
最简不等式
不等式的基本性质
去分母
去括号
移项
合并同类项
系数化为1
步骤
性质2
性质1
性质2
没什么新鲜的,跟解一元一次方程差不多……
例 当x在什么范围内取值时,代数式 的值比x+1的值大?
去分母,得
解:根据题意,x应满足不等式
1+2x>3(x+1).
去括号,得
1+2x>3x+3.
移项,合并同类项,得
将未知数系数化为1,得
-x>2.
x<-2.
即当x<-2时,代数式 的值比x+1的值大.
例3 求不等式 的正整数解.
去分母,得
解:
3(x+1) ≥2(2x-1).
去括号,得
3x+3≥4x-2.
移项,合并同类项,得
将未知数系数化为1,得
-x≥-5.
x ≤ 5.
所以,满足这个不等式的正整数解为x=1,2,3,4,5.
解不等式,并把它的解集表示在数轴上.
做一做
一元一次不等式与一次函数
答案:
当x> 时,y1<y2;
当x= 时,y1=y2;
当x< 时,y1>y2.
例、若y1=-x+3,y2=3x-4,试确定当x取何值时
(1)y1<y2?
(2)y1=y2?
(3)y1>y2?
根据不等式的性质1,在不等式的两边都减去70,得
3x+70-70>100-70
合并同类项,得
3x>30
根据不等式的性质2,在不等式的两边都除以3,得
x>10
这个不等式的解集在数轴上表示如下:
0
10
其实这就是移项
计算:3x+70>100
解不等式,并在数轴上表示解集:
解:去分母,得 3(x-3)<2(2x-5),
去括号,得 3x-9<4x-10,
移项,得 3x-4x<-10+9,
合并同类项,得 -x<-1,
系数化为1,得 x>1 .
<
它在数轴上表示如下:
0
1
小结:
这堂课的目标是掌握一元一次不等式的解题步骤,并学会解一元一次不等式.
你达到目标了没有?谈谈你今天的收获.
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
