2020-2021年北师大版七年级数学下册 4.3.3 探索三角形全等的条件(43张)
文档属性
| 名称 | 2020-2021年北师大版七年级数学下册 4.3.3 探索三角形全等的条件(43张) |  | |
| 格式 | pptx | ||
| 文件大小 | 880.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 18:12:27 | ||
图片预览








文档简介
第四章 三角形
第3课时 探索三角形全等的条件
学习目标
1.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
2.(课标)掌握基本事实:两边及其夹角分别相等的两个三角形全等.
3.在探索三角形全等条件及其应用过程中,能够进行有条理地思考并进行简单地推理.
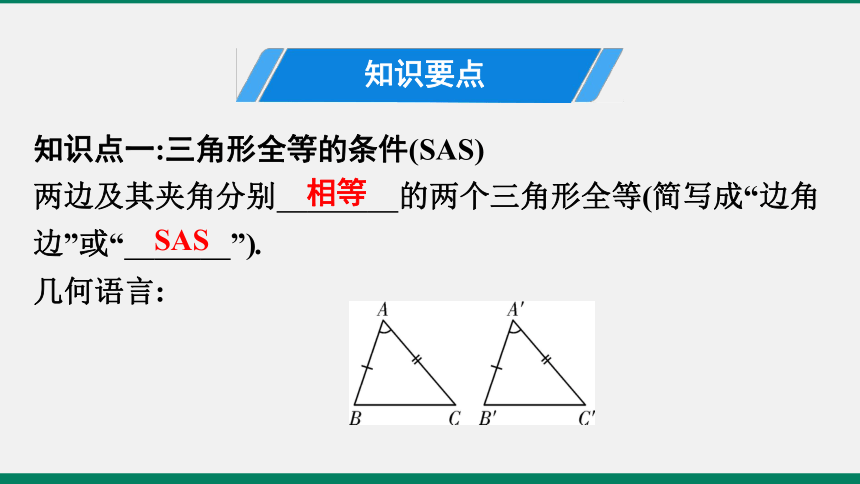
知识点一:三角形全等的条件(SAS)
两边及其夹角分别 的两个三角形全等(简写成“边角边”或“ ”).?
几何语言:
SAS
知识要点
相等
△A'B'C'
SAS
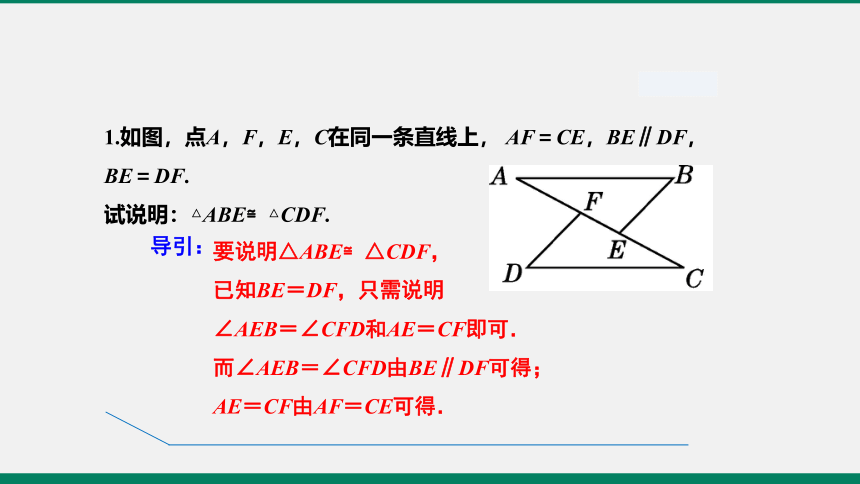
1.如图,点A,F,E,C在同一条直线上, AF=CE,BE∥DF,BE=DF.
试说明:△ABE≌△CDF.
要说明△ABE≌△CDF,
已知BE=DF,只需说明
∠AEB=∠CFD和AE=CF即可.
而∠AEB=∠CFD由BE∥DF可得;
AE=CF由AF=CE可得.
导引:
因为BE∥DF,所以∠AEB=∠CFD.
又因为AF=CE,所以AF+FE=CE+EF,
即AE=CF.
在△ABE和△CDF中,因为
所以△ABE≌△CDF (SAS).
解:
(1)要判断两个三角形全等,若已知两边相等,可考虑说明
第三边相等或两边的夹角相等,是选用“SSS”还是“SAS”
要根据题目的条件而定,如本题由条件BE∥DF可得角的
关系,故用“SAS”说明.
(2)判断两个三角形全等时,常要说明边相等,而说明边相等
的方法有:①公共边;②等线段加(减)等线段其和(差)相等,
即等式性质;③由中点得到线段相等;④同等于第三条线
段的两线段相等,即等量代换;⑤全等三角形的对应边相
等等.
小 结
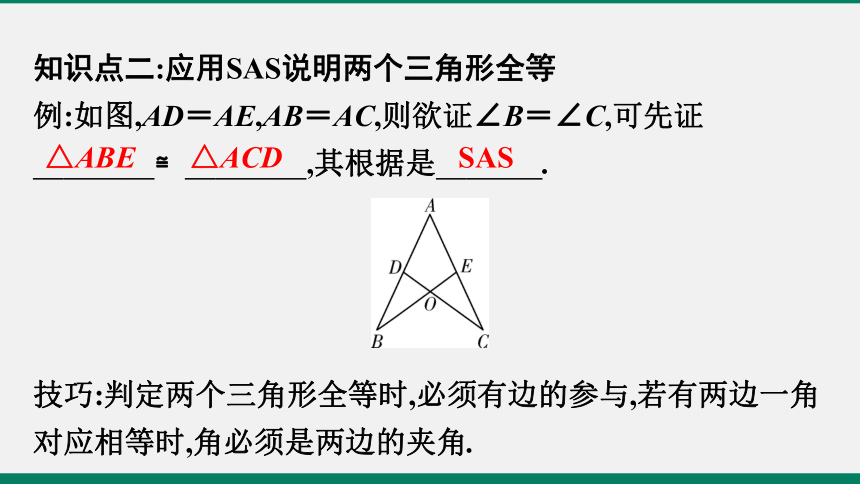
技巧:判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
知识点二:应用SAS说明两个三角形全等
例:如图,AD=AE,AB=AC,则欲证∠B=∠C,可先证
≌ ,其根据是 .?
SAS
△ACD
△ABE
2.〈武汉〉如图,AC和BD相交于点O,OA=OC,
OB=OD.试说明:DC∥AB.
根据“边角边”可说明
△ODC≌△OBA,
可得∠C=∠A(或者∠D=∠B),
即可说明DC∥AB.
导引:
在△ODC和△OBA中,因为
所以△ODC≌△OBA(SAS).
所以∠C=∠A(或者∠D=∠B)(全等三角形的对应
角相等),
所以DC∥AB(内错角相等,两直线平行).
解:
本题可运用分析法寻找说明思路,分析法就是执
果索因,由未知看需知,思维方式上就是从问题入手,
找能求出问题所需要的条件或可行思路,若问题需要
的条件未知,则把所需条件当作中间问题,再找出解
决中间问题的条件.
小 结
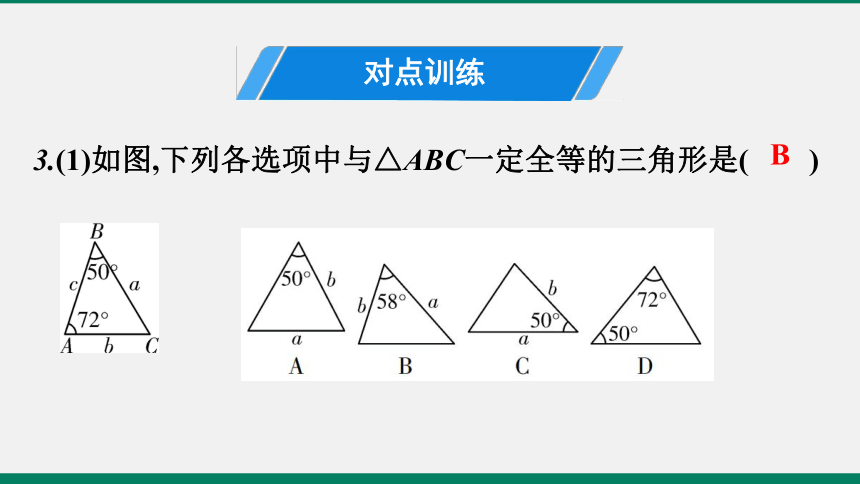
3.(1)如图,下列各选项中与△ABC一定全等的三角形是( )
对点训练
B
(2)如图,AB平分∠DAC,要用SAS确定△ABC≌△ABD,还需要添加的一个条件是 .?
AC=AD
4.如图,线段AC,BD相交于点E,AE=DE,BE=CE,试说明:
△ABE≌△DCE.
5.(新题速递)(2020北京)如图,在△ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可说明△ABD≌△ACD,这个条件可以是______________________ (写出一个即可).?
BD=CD(答案不唯一)
知识点三:运用全等三角形的条件与性质解决问题
如图,已知AC,BD相交于点O,AO=DO,BO=CO.试说明:△ABO≌△DCO.
(1)试说明:△ABC≌△DEF;
(2)若∠F+∠FED=80°,则∠A的度数为 .?
6.如图,点F,B,E,C在同一条直线上,AC=DF,BF=EC,∠F=∠C.
100°
解:(1)因为BF=EC,
所以FE=CB,又∠F=∠C,AC=DF,
所以△ABC≌△DEF(SAS).
7.(2020广州)如图,AB=AD,∠BAC=∠DAC=25°,
∠D=80°.求∠BCA的度数.
8.〈创新应用题〉如图所示,在湖的两岸点A,B之间建一座观赏桥,由于条件限制,无法直接测量A,B两点之间的距离.请你用学过的数学知识按以下要求设计一个测量方案.
(1)画出测量示意图;
(2)写出测量步骤;
(3)计算点A,B之间的距离(写出求
解或推理过程,结果用字母表示).
本题让我们了解了测量两点之间距离的一种方法,设计
时,只要需要测量的线段在陆地一侧可实施,就可以达
到目的.
导引:
(1)如图.
(2)在湖岸上找到可以直接到达点A,B
的一点O,连接BO并延长到点C,
使OC=OB;连接AO并延长到点D,
使OD=OA,连接CD,则测量出CD的
长度即为AB的长度.
(3)设CD=m.
因为OD=OA,OC=OB,∠COD=∠BOA,
所以△COD≌△BOA(SAS),
所以CD=AB,即AB=m.
解:
解答本题的关键是构造全等三角形,巧妙地借助
两个三角形全等,寻找所求线段与已知线段之间的等
量关系.
小 结
9.如图,点B,F,C,E在同一直线上,∠1=∠2,BF=EC,要使△ABC≌△DEF,还需添加的一个条件是
(只需写出一个即可).?
精典范例
AC=DF(答案不唯一)
10.(2020中山模拟)如图,BC=EF,AC∥DF,请你添加一个适当的条件是 (只需填一个答案即可),使得△ABC≌△DEF.?
变式练习
AC=DF(答案不唯一)
A.1
B.2
C.3
D.4
11.如图,射线AB交CD于O,AC=AD,BC=BD,则图中全等三角形的对数是( )
C
A.2
B.3
C.4
D.5
12.如图,点E,F在线段BC上,BE=CF,DE=DF,AD⊥BC,垂足为点D,则图中全等三角形的对数是( )
C
13.如图,AB=DE,AB∥DE,BE=CF.试说明:△ABC≌△DEF.
14.如图,A,D,F,B在同一直线上,AD=BF,AE=BC,且AE∥BC.试说明:△AEF≌△BCD.
15.如图,CA=CD,∠1=∠2,BC=EC.
(1)试说明:AB=DE;
(2)当∠A=21°,∠E=39°时,求∠ACB的度数.
所以△ABC≌△DEC(SAS).所以AB=DE.
(2)因为△ABC≌△DEC,所以∠B=∠E=39°,
所以∠ACB=180°-∠A-∠B=120°.
16.如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,
∠1=∠2.
试说明:(1)△ABE≌△CBD;
(2)∠1=∠3.
(2)因为△ABE≌△CBD,所以∠A=∠C,
因为∠AFB=∠CFE,所以∠1=∠3.
17.(新题速递)(2020河池改编)(1)如图1,已知CE与AB交于点E,AC=BC,∠1=∠2.试说明:△ACE≌△BCE;
(2)如图2,已知CD的延长线与AB交于点E,AD=BC,∠3=∠4,CF=DE.比较∠BEF与∠EFB的大小关系,并说明理由.
(1) 本节课学习了哪些主要内容?
(2) 我们是怎么探究出“SAS”判定方法的?用
“SAS”判定三角形全等应注意什么问题?
(3) 到现在为止,你学到了几种证明两个三角形
全等的方法?
总 结
第3课时 探索三角形全等的条件
学习目标
1.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
2.(课标)掌握基本事实:两边及其夹角分别相等的两个三角形全等.
3.在探索三角形全等条件及其应用过程中,能够进行有条理地思考并进行简单地推理.
知识点一:三角形全等的条件(SAS)
两边及其夹角分别 的两个三角形全等(简写成“边角边”或“ ”).?
几何语言:
SAS
知识要点
相等
△A'B'C'
SAS
1.如图,点A,F,E,C在同一条直线上, AF=CE,BE∥DF,BE=DF.
试说明:△ABE≌△CDF.
要说明△ABE≌△CDF,
已知BE=DF,只需说明
∠AEB=∠CFD和AE=CF即可.
而∠AEB=∠CFD由BE∥DF可得;
AE=CF由AF=CE可得.
导引:
因为BE∥DF,所以∠AEB=∠CFD.
又因为AF=CE,所以AF+FE=CE+EF,
即AE=CF.
在△ABE和△CDF中,因为
所以△ABE≌△CDF (SAS).
解:
(1)要判断两个三角形全等,若已知两边相等,可考虑说明
第三边相等或两边的夹角相等,是选用“SSS”还是“SAS”
要根据题目的条件而定,如本题由条件BE∥DF可得角的
关系,故用“SAS”说明.
(2)判断两个三角形全等时,常要说明边相等,而说明边相等
的方法有:①公共边;②等线段加(减)等线段其和(差)相等,
即等式性质;③由中点得到线段相等;④同等于第三条线
段的两线段相等,即等量代换;⑤全等三角形的对应边相
等等.
小 结
技巧:判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
知识点二:应用SAS说明两个三角形全等
例:如图,AD=AE,AB=AC,则欲证∠B=∠C,可先证
≌ ,其根据是 .?
SAS
△ACD
△ABE
2.〈武汉〉如图,AC和BD相交于点O,OA=OC,
OB=OD.试说明:DC∥AB.
根据“边角边”可说明
△ODC≌△OBA,
可得∠C=∠A(或者∠D=∠B),
即可说明DC∥AB.
导引:
在△ODC和△OBA中,因为
所以△ODC≌△OBA(SAS).
所以∠C=∠A(或者∠D=∠B)(全等三角形的对应
角相等),
所以DC∥AB(内错角相等,两直线平行).
解:
本题可运用分析法寻找说明思路,分析法就是执
果索因,由未知看需知,思维方式上就是从问题入手,
找能求出问题所需要的条件或可行思路,若问题需要
的条件未知,则把所需条件当作中间问题,再找出解
决中间问题的条件.
小 结
3.(1)如图,下列各选项中与△ABC一定全等的三角形是( )
对点训练
B
(2)如图,AB平分∠DAC,要用SAS确定△ABC≌△ABD,还需要添加的一个条件是 .?
AC=AD
4.如图,线段AC,BD相交于点E,AE=DE,BE=CE,试说明:
△ABE≌△DCE.
5.(新题速递)(2020北京)如图,在△ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可说明△ABD≌△ACD,这个条件可以是______________________ (写出一个即可).?
BD=CD(答案不唯一)
知识点三:运用全等三角形的条件与性质解决问题
如图,已知AC,BD相交于点O,AO=DO,BO=CO.试说明:△ABO≌△DCO.
(1)试说明:△ABC≌△DEF;
(2)若∠F+∠FED=80°,则∠A的度数为 .?
6.如图,点F,B,E,C在同一条直线上,AC=DF,BF=EC,∠F=∠C.
100°
解:(1)因为BF=EC,
所以FE=CB,又∠F=∠C,AC=DF,
所以△ABC≌△DEF(SAS).
7.(2020广州)如图,AB=AD,∠BAC=∠DAC=25°,
∠D=80°.求∠BCA的度数.
8.〈创新应用题〉如图所示,在湖的两岸点A,B之间建一座观赏桥,由于条件限制,无法直接测量A,B两点之间的距离.请你用学过的数学知识按以下要求设计一个测量方案.
(1)画出测量示意图;
(2)写出测量步骤;
(3)计算点A,B之间的距离(写出求
解或推理过程,结果用字母表示).
本题让我们了解了测量两点之间距离的一种方法,设计
时,只要需要测量的线段在陆地一侧可实施,就可以达
到目的.
导引:
(1)如图.
(2)在湖岸上找到可以直接到达点A,B
的一点O,连接BO并延长到点C,
使OC=OB;连接AO并延长到点D,
使OD=OA,连接CD,则测量出CD的
长度即为AB的长度.
(3)设CD=m.
因为OD=OA,OC=OB,∠COD=∠BOA,
所以△COD≌△BOA(SAS),
所以CD=AB,即AB=m.
解:
解答本题的关键是构造全等三角形,巧妙地借助
两个三角形全等,寻找所求线段与已知线段之间的等
量关系.
小 结
9.如图,点B,F,C,E在同一直线上,∠1=∠2,BF=EC,要使△ABC≌△DEF,还需添加的一个条件是
(只需写出一个即可).?
精典范例
AC=DF(答案不唯一)
10.(2020中山模拟)如图,BC=EF,AC∥DF,请你添加一个适当的条件是 (只需填一个答案即可),使得△ABC≌△DEF.?
变式练习
AC=DF(答案不唯一)
A.1
B.2
C.3
D.4
11.如图,射线AB交CD于O,AC=AD,BC=BD,则图中全等三角形的对数是( )
C
A.2
B.3
C.4
D.5
12.如图,点E,F在线段BC上,BE=CF,DE=DF,AD⊥BC,垂足为点D,则图中全等三角形的对数是( )
C
13.如图,AB=DE,AB∥DE,BE=CF.试说明:△ABC≌△DEF.
14.如图,A,D,F,B在同一直线上,AD=BF,AE=BC,且AE∥BC.试说明:△AEF≌△BCD.
15.如图,CA=CD,∠1=∠2,BC=EC.
(1)试说明:AB=DE;
(2)当∠A=21°,∠E=39°时,求∠ACB的度数.
所以△ABC≌△DEC(SAS).所以AB=DE.
(2)因为△ABC≌△DEC,所以∠B=∠E=39°,
所以∠ACB=180°-∠A-∠B=120°.
16.如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,
∠1=∠2.
试说明:(1)△ABE≌△CBD;
(2)∠1=∠3.
(2)因为△ABE≌△CBD,所以∠A=∠C,
因为∠AFB=∠CFE,所以∠1=∠3.
17.(新题速递)(2020河池改编)(1)如图1,已知CE与AB交于点E,AC=BC,∠1=∠2.试说明:△ACE≌△BCE;
(2)如图2,已知CD的延长线与AB交于点E,AD=BC,∠3=∠4,CF=DE.比较∠BEF与∠EFB的大小关系,并说明理由.
(1) 本节课学习了哪些主要内容?
(2) 我们是怎么探究出“SAS”判定方法的?用
“SAS”判定三角形全等应注意什么问题?
(3) 到现在为止,你学到了几种证明两个三角形
全等的方法?
总 结
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
