2020-2021年北师大版七年级数学下册 4.3.2 探索三角形全等的条件课件(39张)
文档属性
| 名称 | 2020-2021年北师大版七年级数学下册 4.3.2 探索三角形全等的条件课件(39张) |  | |
| 格式 | pptx | ||
| 文件大小 | 784.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 18:14:23 | ||
图片预览





文档简介
第四章 三角形
第2课时 探索三角形全等的条件
学习目标
1.(课标)掌握基本事实:两角及其夹边分别相等的两个三角形全等.
2.(课标)掌握基本事实:两角分别相等且其中一组等角的对边相等的两个三角形全等.
3.在探索三角形全等条件及其应用过程中,能够进行有条理地思考并进行简单地推理.
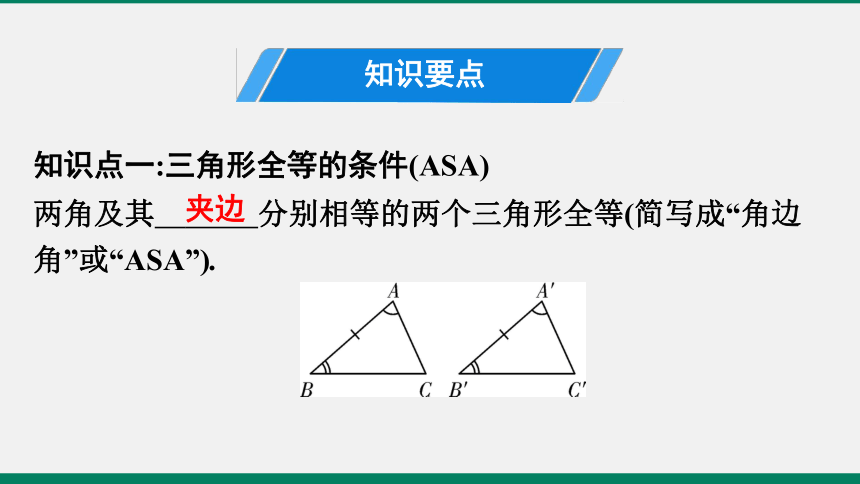
知识点一:三角形全等的条件(ASA)
两角及其 分别相等的两个三角形全等(简写成“角边角”或“ASA”).?
知识要点
夹边
几何语言:
在△ABC与△A'B'C'中,
△A'B'C'
ASA
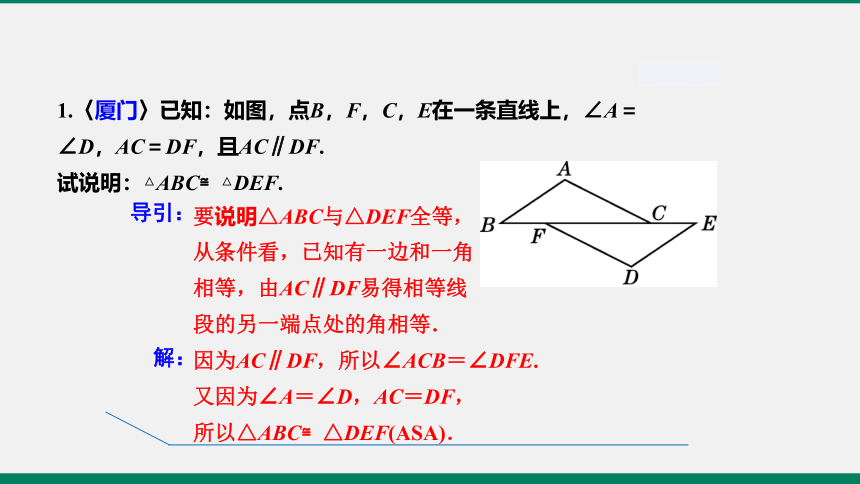
1.〈厦门〉已知:如图,点B,F,C,E在一条直线上,∠A=∠D,AC=DF,且AC∥DF.
试说明:△ABC≌△DEF.
要说明△ABC与△DEF全等,
从条件看,已知有一边和一角
相等,由AC∥DF易得相等线
段的另一端点处的角相等.
因为AC∥DF,所以∠ACB=∠DFE.
又因为∠A=∠D,AC=DF,
所以△ABC≌△DEF(ASA).
导引:
解:
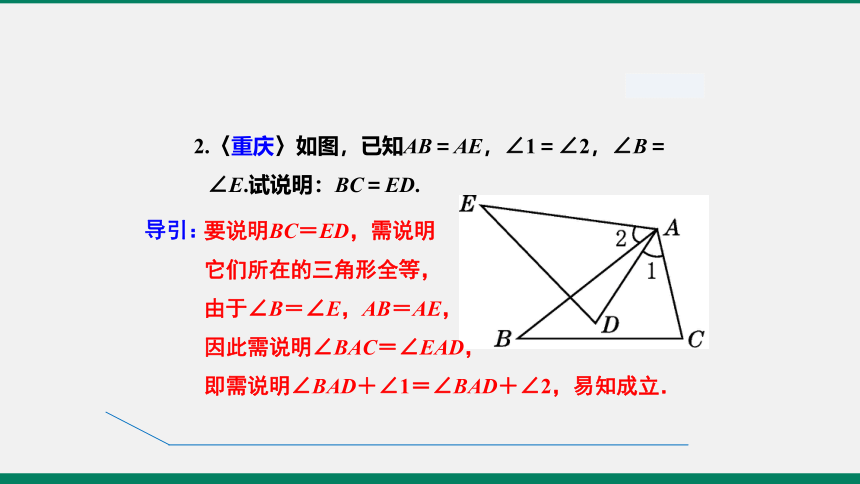
2.〈重庆〉如图,已知AB=AE,∠1=∠2,∠B=∠E.试说明:BC=ED.
要说明BC=ED,需说明
它们所在的三角形全等,
由于∠B=∠E,AB=AE,
因此需说明∠BAC=∠EAD,
即需说明∠BAD+∠1=∠BAD+∠2,易知成立.
导引:
因为∠1=∠2,
所以∠1+∠BAD=∠2+∠BAD,
即∠BAC=∠EAD.
在△BAC和△EAD中,因为
所以△BAC≌△EAD(ASA).
所以BC=ED.
解:
在说明两个三角形全等所需要的角相等时,目前
通常采用的方法有:(1)公共角、对顶角分别相等;
(2)等角加(减)等角,其和(差)相等,即等式的性质;
(3)同角或等角的余(补)角相等;(4)角平分线得到相等角;
(5)平行线的同位角、内错角相等;(6)直角都相等;
(7)全等三角形对应角相等;(8)第三角代换,即等量代
换等.
小结
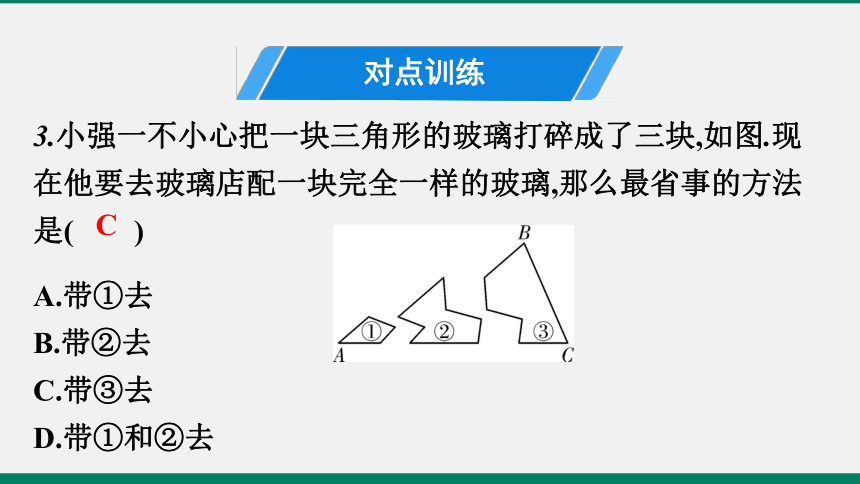
A.带①去
B.带②去
C.带③去
D.带①和②去
3.小强一不小心把一块三角形的玻璃打碎成了三块,如图.现在他要去玻璃店配一块完全一样的玻璃,那么最省事的方法是( )
对点训练
C
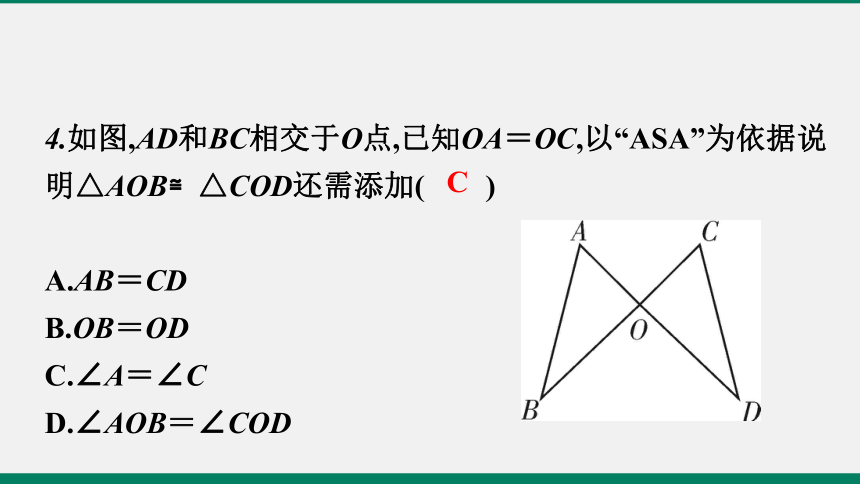
4.如图,AD和BC相交于O点,已知OA=OC,以“ASA”为依据说明△AOB≌△COD还需添加( )
?
A.AB=CD
B.OB=OD
C.∠A=∠C
D.∠AOB=∠COD
C
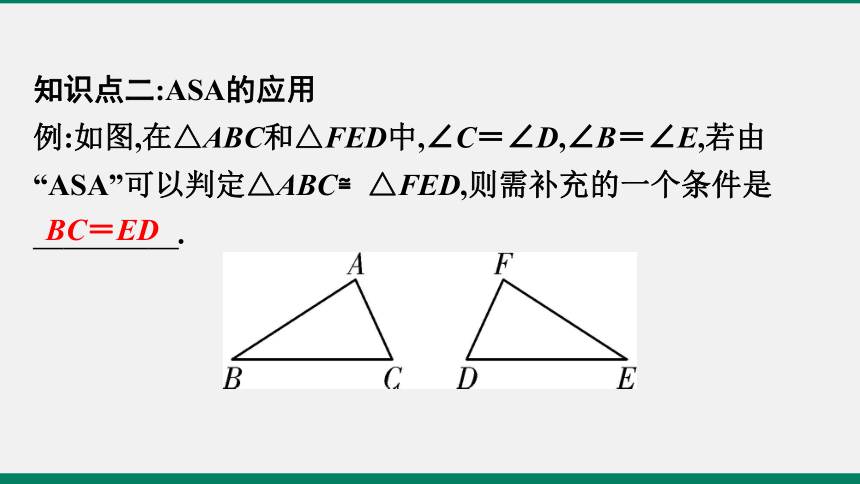
知识点二:ASA的应用
例:如图,在△ABC和△FED中,∠C=∠D,∠B=∠E,若由“ASA”可以判定△ABC≌△FED,则需补充的一个条件是
.?
BC=ED
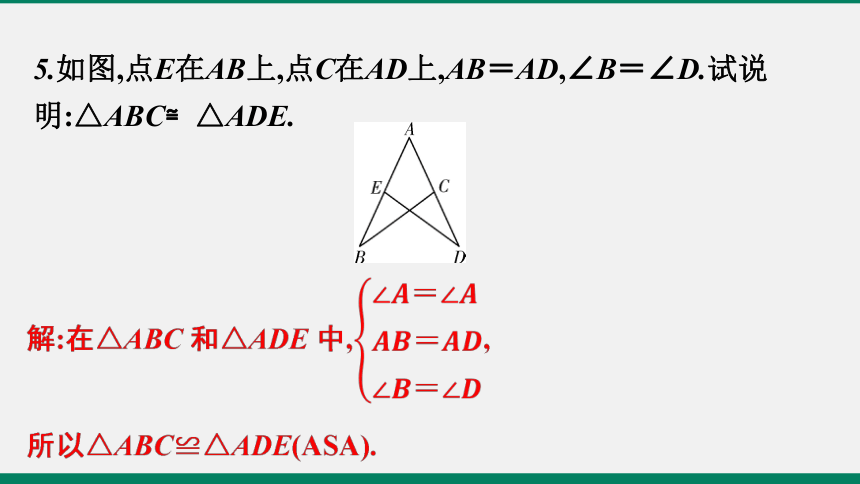
5.如图,点E在AB上,点C在AD上,AB=AD,∠B=∠D.试说明:△ABC≌△ADE.
知识点三:三角形全等的条件(AAS)
两角分别相等且其中一组等角的对边 的两个三角形全等(简写成“角角边”或“AAS”).?
几何语言:
相等
△A'B'C'
AAS
6.如图,已知AC=EC,∠ACB=∠ECD,要利用“AAS”判定△ABC≌△EDC,应添加的条件是 .?
∠B=∠D
例:如图,已知∠B=∠DEF,AB=DE,要说明△ABC≌△DEF.
(1)若以“ASA”为依据,还缺条件为 ;?
(2)若以“AAS”为依据,还缺条件为 .?
∠ACB=∠DFE
知识点四:AAS的应用
∠A=∠D
7.如图,∠1=∠2,AD=AB,∠AED=∠C,试说明:△ADE≌△ABC.
8.如图,AD是△ABC的中线,过点C,B分别作AD的垂线CF,BE.试说明:BE=CF.
要说明BE=CF,可根据中线
及垂线的定义和对顶角的性质
来说明△BDE和△CDF全等.
导引:
因为AD是△ABC的中线,所以BD=CD.
因为CF⊥AD,BE⊥AE,
所以∠CFD=∠BED=90°.
在△BDE和△CDF中,因为
所以△BDE≌△CDF(AAS).
所以BE=CF.
解:
利用两个三角形全等解决问题,先根据已知条件
或要说明的结论确定三角形,然后再根据三角形全等
的判定方法看缺什么条件,再去说明什么条件,简言
之:即综合利用分析法和综合法寻找解题的途径.
小 结
9.如图,在四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.
试说明:△ABC与△DEC全等.
如图,因为∠BCE=∠ACD=90°,
所以∠3+∠4=∠4+∠5.
所以∠3=∠5.
在△ACD中,∠ACD=90°,
所以∠2+∠D=90°.
因为∠BAE=∠1+∠2=90°,
所以∠1=∠D.
在△ABC和△DEC中,
所以△ABC≌△DEC.
解:
10.我们把两组邻边相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD.对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是
E,F.
试说明:OE=OF.
因为在△ABD和△CBD中,
所以△ABD≌△CBD(SSS).
所以∠ABD=∠CBD.
又因为OE⊥AB,OF⊥CB,所以∠OEB=∠OFB.
在△BOE和△BOF中,
所以△BOE≌△BOF(AAS).
所以OE=OF.
解:
A.SSS B.AAS C.SAS D.ASA
11.如图,CE⊥AB,DF⊥AB,垂足分别为E,F,AC∥DB,且AE=BF,那么△AEC≌△BFD的理由是( )
精典范例
D
A.∠ACB=∠F B.AB=DF
C.AB=DE D.AC=DF
12.如图,点B,E,C,F在同一直线上,已知∠A=∠D,∠B=∠DEF,要直接利用AAS说明△ABC≌△DEF,可补充的条件是( )
变式练习
D
13.如图,BE与CD交于点A,且∠C=∠D.添加一个条件:
,使得△ABC≌△AED.?
AC=AD(答案不唯一)
14.如图,∠A=∠D,要使△ABC≌△DBC,还需要补充一个条件: (填一个即可).?
∠ABC=∠DBC(或∠ACB=∠DCB)
15.如图,点B,F,C,E在一条直线上,BF=CE,
AB∥DE,∠A=∠D.试说明:AC=DF.
16.如图,点C,F在BE上,BF=EC,AB∥DE,且∠A=∠D,试说明:AC=DF.
17.如图,在△ABC中,高AD与BE相交于点H,且AD=BD,问△BHD≌△ACD吗?为什么?
★18.如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=5 cm,DE=3 cm,求BE的长度.
所以△BEC≌△CDA(AAS).
所以CE=AD=5 cm,BE=CD,
因为DE=3 cm,所以BE=CD=5-3=2 cm.
1.利用“角边角“判定两三角形全等:
2.利用“角角边“判定两三角形全等:
总 结
第2课时 探索三角形全等的条件
学习目标
1.(课标)掌握基本事实:两角及其夹边分别相等的两个三角形全等.
2.(课标)掌握基本事实:两角分别相等且其中一组等角的对边相等的两个三角形全等.
3.在探索三角形全等条件及其应用过程中,能够进行有条理地思考并进行简单地推理.
知识点一:三角形全等的条件(ASA)
两角及其 分别相等的两个三角形全等(简写成“角边角”或“ASA”).?
知识要点
夹边
几何语言:
在△ABC与△A'B'C'中,
△A'B'C'
ASA
1.〈厦门〉已知:如图,点B,F,C,E在一条直线上,∠A=∠D,AC=DF,且AC∥DF.
试说明:△ABC≌△DEF.
要说明△ABC与△DEF全等,
从条件看,已知有一边和一角
相等,由AC∥DF易得相等线
段的另一端点处的角相等.
因为AC∥DF,所以∠ACB=∠DFE.
又因为∠A=∠D,AC=DF,
所以△ABC≌△DEF(ASA).
导引:
解:
2.〈重庆〉如图,已知AB=AE,∠1=∠2,∠B=∠E.试说明:BC=ED.
要说明BC=ED,需说明
它们所在的三角形全等,
由于∠B=∠E,AB=AE,
因此需说明∠BAC=∠EAD,
即需说明∠BAD+∠1=∠BAD+∠2,易知成立.
导引:
因为∠1=∠2,
所以∠1+∠BAD=∠2+∠BAD,
即∠BAC=∠EAD.
在△BAC和△EAD中,因为
所以△BAC≌△EAD(ASA).
所以BC=ED.
解:
在说明两个三角形全等所需要的角相等时,目前
通常采用的方法有:(1)公共角、对顶角分别相等;
(2)等角加(减)等角,其和(差)相等,即等式的性质;
(3)同角或等角的余(补)角相等;(4)角平分线得到相等角;
(5)平行线的同位角、内错角相等;(6)直角都相等;
(7)全等三角形对应角相等;(8)第三角代换,即等量代
换等.
小结
A.带①去
B.带②去
C.带③去
D.带①和②去
3.小强一不小心把一块三角形的玻璃打碎成了三块,如图.现在他要去玻璃店配一块完全一样的玻璃,那么最省事的方法是( )
对点训练
C
4.如图,AD和BC相交于O点,已知OA=OC,以“ASA”为依据说明△AOB≌△COD还需添加( )
?
A.AB=CD
B.OB=OD
C.∠A=∠C
D.∠AOB=∠COD
C
知识点二:ASA的应用
例:如图,在△ABC和△FED中,∠C=∠D,∠B=∠E,若由“ASA”可以判定△ABC≌△FED,则需补充的一个条件是
.?
BC=ED
5.如图,点E在AB上,点C在AD上,AB=AD,∠B=∠D.试说明:△ABC≌△ADE.
知识点三:三角形全等的条件(AAS)
两角分别相等且其中一组等角的对边 的两个三角形全等(简写成“角角边”或“AAS”).?
几何语言:
相等
△A'B'C'
AAS
6.如图,已知AC=EC,∠ACB=∠ECD,要利用“AAS”判定△ABC≌△EDC,应添加的条件是 .?
∠B=∠D
例:如图,已知∠B=∠DEF,AB=DE,要说明△ABC≌△DEF.
(1)若以“ASA”为依据,还缺条件为 ;?
(2)若以“AAS”为依据,还缺条件为 .?
∠ACB=∠DFE
知识点四:AAS的应用
∠A=∠D
7.如图,∠1=∠2,AD=AB,∠AED=∠C,试说明:△ADE≌△ABC.
8.如图,AD是△ABC的中线,过点C,B分别作AD的垂线CF,BE.试说明:BE=CF.
要说明BE=CF,可根据中线
及垂线的定义和对顶角的性质
来说明△BDE和△CDF全等.
导引:
因为AD是△ABC的中线,所以BD=CD.
因为CF⊥AD,BE⊥AE,
所以∠CFD=∠BED=90°.
在△BDE和△CDF中,因为
所以△BDE≌△CDF(AAS).
所以BE=CF.
解:
利用两个三角形全等解决问题,先根据已知条件
或要说明的结论确定三角形,然后再根据三角形全等
的判定方法看缺什么条件,再去说明什么条件,简言
之:即综合利用分析法和综合法寻找解题的途径.
小 结
9.如图,在四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.
试说明:△ABC与△DEC全等.
如图,因为∠BCE=∠ACD=90°,
所以∠3+∠4=∠4+∠5.
所以∠3=∠5.
在△ACD中,∠ACD=90°,
所以∠2+∠D=90°.
因为∠BAE=∠1+∠2=90°,
所以∠1=∠D.
在△ABC和△DEC中,
所以△ABC≌△DEC.
解:
10.我们把两组邻边相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD.对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是
E,F.
试说明:OE=OF.
因为在△ABD和△CBD中,
所以△ABD≌△CBD(SSS).
所以∠ABD=∠CBD.
又因为OE⊥AB,OF⊥CB,所以∠OEB=∠OFB.
在△BOE和△BOF中,
所以△BOE≌△BOF(AAS).
所以OE=OF.
解:
A.SSS B.AAS C.SAS D.ASA
11.如图,CE⊥AB,DF⊥AB,垂足分别为E,F,AC∥DB,且AE=BF,那么△AEC≌△BFD的理由是( )
精典范例
D
A.∠ACB=∠F B.AB=DF
C.AB=DE D.AC=DF
12.如图,点B,E,C,F在同一直线上,已知∠A=∠D,∠B=∠DEF,要直接利用AAS说明△ABC≌△DEF,可补充的条件是( )
变式练习
D
13.如图,BE与CD交于点A,且∠C=∠D.添加一个条件:
,使得△ABC≌△AED.?
AC=AD(答案不唯一)
14.如图,∠A=∠D,要使△ABC≌△DBC,还需要补充一个条件: (填一个即可).?
∠ABC=∠DBC(或∠ACB=∠DCB)
15.如图,点B,F,C,E在一条直线上,BF=CE,
AB∥DE,∠A=∠D.试说明:AC=DF.
16.如图,点C,F在BE上,BF=EC,AB∥DE,且∠A=∠D,试说明:AC=DF.
17.如图,在△ABC中,高AD与BE相交于点H,且AD=BD,问△BHD≌△ACD吗?为什么?
★18.如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=5 cm,DE=3 cm,求BE的长度.
所以△BEC≌△CDA(AAS).
所以CE=AD=5 cm,BE=CD,
因为DE=3 cm,所以BE=CD=5-3=2 cm.
1.利用“角边角“判定两三角形全等:
2.利用“角角边“判定两三角形全等:
总 结
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
