11.5 用一元一次不等式解决问题(第1课时) 课件(共25张PPT)
文档属性
| 名称 | 11.5 用一元一次不等式解决问题(第1课时) 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 18:15:23 | ||
图片预览








文档简介
第1课时
11.5 用一元一次不等式解决问题
第11章 一元一次不等式
2020-2021学年度苏科版七年级下册
问题1 一只纸箱质量为1kg,放人一些苹果后,纸箱和苹果的总质量不超过10kg.假设每个苹果的质量为0.25kg,这只纸箱内最多能装多少个苹果?
答:这只纸箱内最多能装36个苹果.
x≤36.
解这个不等式,得
0.25x+1≤10.
解:设这只纸箱内装了x个苹果.
根据题意,得
问题2 某种杜鹃花适宜生长在平均气温为17°C到20°C之间的山区.已知某山区山脚下的平均气温为20°C,并且每上升100m,气温下降0.6°C,求该山区适宜种植这种杜鹃花的山坡的高度.
解:设这种杜鹃花适宜种植在该山区高度为xm的山坡上,那么这个区域的平均气温是 °C.
根据题意,得
答:这种杜鹃花适宜种植在该山区高度不超过500m的山坡上.
x≤500.
解这个不等式,得
动脑筋
小华打算在星期天与同学去登山,计划上午7点出发,到达山顶后休息2h,下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶?(图中数字表示出发点到山顶的路程.)
问题中涉及的数量关系是:
去时所花时间+休息时间+回来所花时间≤总时间.
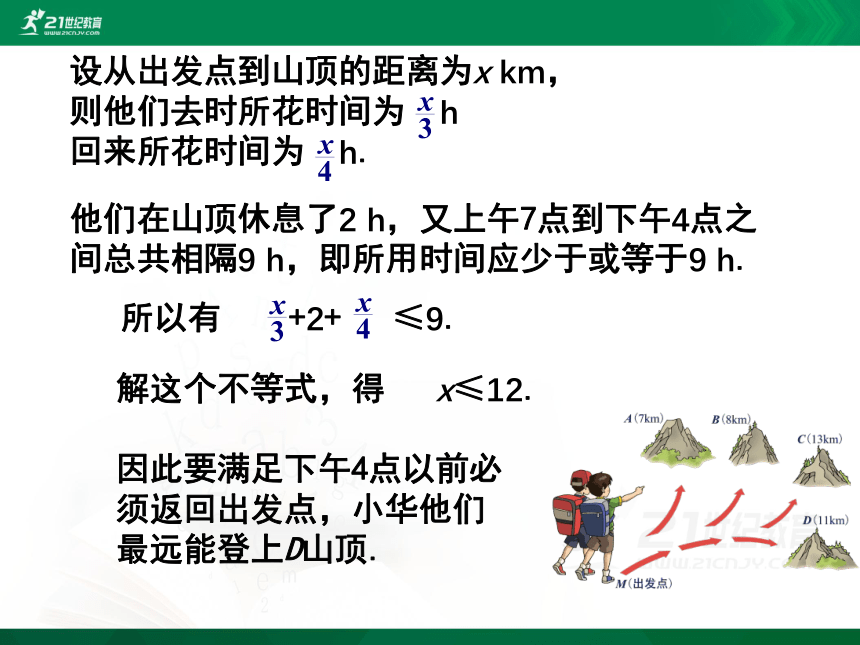
设从出发点到山顶的距离为x km,
则他们去时所花时间为 h
回来所花时间为 h.
他们在山顶休息了2 h,又上午7点到下午4点之间总共相隔9 h,即所用时间应少于或等于9 h.
所以有 +2+ ≤9.
解这个不等式,得 x≤12.
因此要满足下午4点以前必须返回出发点,小华他们最远能登上D山顶.
问题3 某人骑一辆变速自行车,如果行驶速度增加4km/h,那么2h所行驶的路程不少于以原来速度2.5h所行驶的路程.原来行驶的速度最大是多少?
2(x+4) ≥2.5x.
解:设原来行驶的速度是xkm/h.
根据题意,得
答:原来行驶的速度最大是16km/h.
解这个不等式,得
x≤16.
问题4小明有1元和5角的硬币共13枚,这些硬币的总币值小于8.5元.问小明可能有几枚1元的硬币?
答:小明可能有l元硬币0枚,1枚,2枚,3枚.
因为x是自然数,所以x可取0,1,2,3.
x<4.
解这个不等式,得
x+0.5(13-x)<8.5.
解:设小明有1元的硬币x枚.
根据题意,得
某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
设每套童装的售价是x元.
解
则 40·x-90×40-40·x·10%≥900.
解这个不等式,得
x ≥ 125.
答:每套童装的售价至少是125元.
分析 本题涉及的数量关系是:
销售额-成本-税费≥纯利润(900元).
当一个人坐下时,不宜提举超过4.5 kg的重物,以免受伤. 小明坐在书桌前,桌上有两本各重1.2 kg的画册和一批每本重0.4 kg的记事本. 如果小明想坐着搬动这两本画册和一些记事本. 问他最多只应搬动多少本记事本?
设小明最多只应搬动x本记事本,则
解
解这个不等式,得
x≤5.25.
1.2×2+0.4x≤4.5.
答:小明最多只应搬动5本记事本.
由于记事本的数目必须是整数,所以x 的最大值为5.
分析 本题涉及的数量关系是:
画册的总重+记事本的总重≤4.5 kg.
应用一元一次不等式解决实际问题的步骤有哪些?
议一议
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
练习
1.小明家的客厅长5 m,宽4 m.现在想购买边长为60 cm的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
解
设需要购买x块地板砖,则有
5×4≤x·0.6×0.6
解这个不等式,得 x ≥ 55.6
由于地板砖的数目必须是整数,所以x的最小值为56.
答:小明至少要购买56块地板砖.
练习
2.某市打市内电话的收费标准是:每次3 min以内(含3 min)0.22元,以后每分钟0.11元(不足1 min部分按1 min计).小琴一天在家里给同学打了一次市内电话,所用电话费没超过0.5元.她最多打了几分钟的电话?
解
设小琴最多打了x分钟的电话,则有
0.22+ (x-3) ×0.11<0.5
解这个不等式,得 x <5.5
由于电话计时按照分钟计时,x应是整数,所以x的最大值为5.
答:小琴最多打了5分钟的电话.
中考 试题
某学校要印刷一批宣传材料,甲印务公司提出收制版费900元,另外每份材料收印刷费0.5元;乙印务公司提出不收制版费,每份材料收印刷费0.8元.
(1)分别写出两家印务公司的收费y(元)与印刷材料的份数x(份)之间的函数关系式.
(2)若学校预计要印刷5000份以内的宣传材料,请问学校应选择哪一家印务公司更合算?
解
(1)y甲=900+0.5x,y乙=0.8x.
(2)令y甲>y乙,则900+0.5x>0.8x. 解之,得x<3000.
所以,当印刷3000份以内的宣传材料时选乙公司合算;
当印刷3000份以上5000份以内时,应选甲公司更合算.
1.小明家的客厅长5 m,宽4 m.现在想购买边长为60 cm的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
解:设至少需要购买x(x为正整数)块这样的地板,则
0.6×0.6x≥4×5
x≥55.56
答:至少需要购买56块这样的地板砖.
所以x的最小值是56.
2.某市打市内电话的收费标准是:每次3 min以内(含3min)0.22元,以后每分钟0.11元(不足1 min部分按1 min计).小琴一天在家里给同学打了一次市内电话,所用电话费没超过0.5元.她最多打了几分钟的电话?
解:设她最多打了x min的电话,则
(x-3)×0.11+0.22≤0.55
x≤6
答:她最多打了6min的电话.
所以x的最大值是6.
1.如图,小明和爸爸、妈妈三人玩跷跷板,小明和妈妈坐在一端,爸爸坐在另一端.三人的体重一共为150kg,小明的体重是妈妈体重的一半.根据“爸爸这边着地”的情景,指出小明的体重应小于多少千克.
解:设小明的体重为xkg.
则:
x+2x<150-x -2x
6x < 150
x < 25
答:设小明的体重应小于25千克.
2.某服装厂计划生产一种服装,每件成本是60 元,售价是80元.该厂生产这种服装,每月除成本外的其他开支共为5000元.如果想使生产这种服装的月获利不低于20000元,那么每月至少要生产这种服装多少件?
解:每月至少生产这种服装x 件. 则:
80x-60x- 5000≥20000
20x≥25000
x≥1250
答:每月至少生产这种服装1250 件.
某公司40名员工到一景点集体参观,该景点规定满40人可以购买团体票,票价打八折.这天恰逢妇女节,该景点做活动,女士票价打五折,但不能同时享受两种优惠.请你帮助他们选择购票方案.
解:设该公司参观者中有女士x人,选择购买女士五折票时所需费用为y1元,选择购买团体票时所需费用为y2元,则
由y1 = y2,得0.5x+40-x=40×0.8,解得x=16;
由y1 > y2,得0.5x+40-x>40×0.8 ,解得x<16;
由y1 < y2,得0.5x+40-x<40×0.8 ,解得x>16.
;
答:当女士不足16人时,购买团体票合算;当女士恰好是16人时,两种方案所需费用相同;当女士多于16人时,购买女士五折票合算.
1.某种商品的进价为400元,出售时标价为500
元,后来由于该商品积压,商店准备打折出
售,但要保持利润率不低于10%,则至多可
打几折?
解:设至多可以打x折.
故至多可以打88折.
可得不等式500x≥400(1+10%).
化简,得
500x≥440.
两边同除以500,得
x≥0.88.
2.小明准备用26元买火腿肠和方便面,已知一根
火腿肠2元,一盒方便面3元,他买了5盒方便
面 ,他还可能买多少根火腿肠?
解:设他还可能买x根火腿肠,根据题意,得
2x+3×5≤26.
解这个不等式,得
x≤5.5.
因为在这一问题中,x只能取正整数,所以小明还可能买1根、2根、3根、4根或5根火腿肠.
谢谢聆听
11.5 用一元一次不等式解决问题
第11章 一元一次不等式
2020-2021学年度苏科版七年级下册
问题1 一只纸箱质量为1kg,放人一些苹果后,纸箱和苹果的总质量不超过10kg.假设每个苹果的质量为0.25kg,这只纸箱内最多能装多少个苹果?
答:这只纸箱内最多能装36个苹果.
x≤36.
解这个不等式,得
0.25x+1≤10.
解:设这只纸箱内装了x个苹果.
根据题意,得
问题2 某种杜鹃花适宜生长在平均气温为17°C到20°C之间的山区.已知某山区山脚下的平均气温为20°C,并且每上升100m,气温下降0.6°C,求该山区适宜种植这种杜鹃花的山坡的高度.
解:设这种杜鹃花适宜种植在该山区高度为xm的山坡上,那么这个区域的平均气温是 °C.
根据题意,得
答:这种杜鹃花适宜种植在该山区高度不超过500m的山坡上.
x≤500.
解这个不等式,得
动脑筋
小华打算在星期天与同学去登山,计划上午7点出发,到达山顶后休息2h,下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶?(图中数字表示出发点到山顶的路程.)
问题中涉及的数量关系是:
去时所花时间+休息时间+回来所花时间≤总时间.
设从出发点到山顶的距离为x km,
则他们去时所花时间为 h
回来所花时间为 h.
他们在山顶休息了2 h,又上午7点到下午4点之间总共相隔9 h,即所用时间应少于或等于9 h.
所以有 +2+ ≤9.
解这个不等式,得 x≤12.
因此要满足下午4点以前必须返回出发点,小华他们最远能登上D山顶.
问题3 某人骑一辆变速自行车,如果行驶速度增加4km/h,那么2h所行驶的路程不少于以原来速度2.5h所行驶的路程.原来行驶的速度最大是多少?
2(x+4) ≥2.5x.
解:设原来行驶的速度是xkm/h.
根据题意,得
答:原来行驶的速度最大是16km/h.
解这个不等式,得
x≤16.
问题4小明有1元和5角的硬币共13枚,这些硬币的总币值小于8.5元.问小明可能有几枚1元的硬币?
答:小明可能有l元硬币0枚,1枚,2枚,3枚.
因为x是自然数,所以x可取0,1,2,3.
x<4.
解这个不等式,得
x+0.5(13-x)<8.5.
解:设小明有1元的硬币x枚.
根据题意,得
某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
设每套童装的售价是x元.
解
则 40·x-90×40-40·x·10%≥900.
解这个不等式,得
x ≥ 125.
答:每套童装的售价至少是125元.
分析 本题涉及的数量关系是:
销售额-成本-税费≥纯利润(900元).
当一个人坐下时,不宜提举超过4.5 kg的重物,以免受伤. 小明坐在书桌前,桌上有两本各重1.2 kg的画册和一批每本重0.4 kg的记事本. 如果小明想坐着搬动这两本画册和一些记事本. 问他最多只应搬动多少本记事本?
设小明最多只应搬动x本记事本,则
解
解这个不等式,得
x≤5.25.
1.2×2+0.4x≤4.5.
答:小明最多只应搬动5本记事本.
由于记事本的数目必须是整数,所以x 的最大值为5.
分析 本题涉及的数量关系是:
画册的总重+记事本的总重≤4.5 kg.
应用一元一次不等式解决实际问题的步骤有哪些?
议一议
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
练习
1.小明家的客厅长5 m,宽4 m.现在想购买边长为60 cm的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
解
设需要购买x块地板砖,则有
5×4≤x·0.6×0.6
解这个不等式,得 x ≥ 55.6
由于地板砖的数目必须是整数,所以x的最小值为56.
答:小明至少要购买56块地板砖.
练习
2.某市打市内电话的收费标准是:每次3 min以内(含3 min)0.22元,以后每分钟0.11元(不足1 min部分按1 min计).小琴一天在家里给同学打了一次市内电话,所用电话费没超过0.5元.她最多打了几分钟的电话?
解
设小琴最多打了x分钟的电话,则有
0.22+ (x-3) ×0.11<0.5
解这个不等式,得 x <5.5
由于电话计时按照分钟计时,x应是整数,所以x的最大值为5.
答:小琴最多打了5分钟的电话.
中考 试题
某学校要印刷一批宣传材料,甲印务公司提出收制版费900元,另外每份材料收印刷费0.5元;乙印务公司提出不收制版费,每份材料收印刷费0.8元.
(1)分别写出两家印务公司的收费y(元)与印刷材料的份数x(份)之间的函数关系式.
(2)若学校预计要印刷5000份以内的宣传材料,请问学校应选择哪一家印务公司更合算?
解
(1)y甲=900+0.5x,y乙=0.8x.
(2)令y甲>y乙,则900+0.5x>0.8x. 解之,得x<3000.
所以,当印刷3000份以内的宣传材料时选乙公司合算;
当印刷3000份以上5000份以内时,应选甲公司更合算.
1.小明家的客厅长5 m,宽4 m.现在想购买边长为60 cm的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
解:设至少需要购买x(x为正整数)块这样的地板,则
0.6×0.6x≥4×5
x≥55.56
答:至少需要购买56块这样的地板砖.
所以x的最小值是56.
2.某市打市内电话的收费标准是:每次3 min以内(含3min)0.22元,以后每分钟0.11元(不足1 min部分按1 min计).小琴一天在家里给同学打了一次市内电话,所用电话费没超过0.5元.她最多打了几分钟的电话?
解:设她最多打了x min的电话,则
(x-3)×0.11+0.22≤0.55
x≤6
答:她最多打了6min的电话.
所以x的最大值是6.
1.如图,小明和爸爸、妈妈三人玩跷跷板,小明和妈妈坐在一端,爸爸坐在另一端.三人的体重一共为150kg,小明的体重是妈妈体重的一半.根据“爸爸这边着地”的情景,指出小明的体重应小于多少千克.
解:设小明的体重为xkg.
则:
x+2x<150-x -2x
6x < 150
x < 25
答:设小明的体重应小于25千克.
2.某服装厂计划生产一种服装,每件成本是60 元,售价是80元.该厂生产这种服装,每月除成本外的其他开支共为5000元.如果想使生产这种服装的月获利不低于20000元,那么每月至少要生产这种服装多少件?
解:每月至少生产这种服装x 件. 则:
80x-60x- 5000≥20000
20x≥25000
x≥1250
答:每月至少生产这种服装1250 件.
某公司40名员工到一景点集体参观,该景点规定满40人可以购买团体票,票价打八折.这天恰逢妇女节,该景点做活动,女士票价打五折,但不能同时享受两种优惠.请你帮助他们选择购票方案.
解:设该公司参观者中有女士x人,选择购买女士五折票时所需费用为y1元,选择购买团体票时所需费用为y2元,则
由y1 = y2,得0.5x+40-x=40×0.8,解得x=16;
由y1 > y2,得0.5x+40-x>40×0.8 ,解得x<16;
由y1 < y2,得0.5x+40-x<40×0.8 ,解得x>16.
;
答:当女士不足16人时,购买团体票合算;当女士恰好是16人时,两种方案所需费用相同;当女士多于16人时,购买女士五折票合算.
1.某种商品的进价为400元,出售时标价为500
元,后来由于该商品积压,商店准备打折出
售,但要保持利润率不低于10%,则至多可
打几折?
解:设至多可以打x折.
故至多可以打88折.
可得不等式500x≥400(1+10%).
化简,得
500x≥440.
两边同除以500,得
x≥0.88.
2.小明准备用26元买火腿肠和方便面,已知一根
火腿肠2元,一盒方便面3元,他买了5盒方便
面 ,他还可能买多少根火腿肠?
解:设他还可能买x根火腿肠,根据题意,得
2x+3×5≤26.
解这个不等式,得
x≤5.5.
因为在这一问题中,x只能取正整数,所以小明还可能买1根、2根、3根、4根或5根火腿肠.
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
