11.6 一元一次不等式组(第2课时) 课件(共42张PPT)
文档属性
| 名称 | 11.6 一元一次不等式组(第2课时) 课件(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 00:00:00 | ||
图片预览







文档简介
第2课时
11.6 一元一次不等式组
第11章 一元一次不等式
2020-2021学年度苏科版七年级下册
喜羊羊:“懒羊羊,你怎么减肥了?”
懒羊羊:“是的,我的体重由一个月前的18kg降到现在的15kg.”
喜羊羊:“是吗?我现在的体重再加上2kg的话就超过你了,但没超过你原来的体重.”
设喜羊羊现在的体重为 x (kg), 你能列出几个不等式?
由几个同一未知数的一元一次不等式所组成的一组不等式, 叫做一元一次不等式组.
一元一次不等式组
例如
辩一辩
下列式子中,哪些是一元一次不等式组?
不是
不是
√
√
√
√
不是
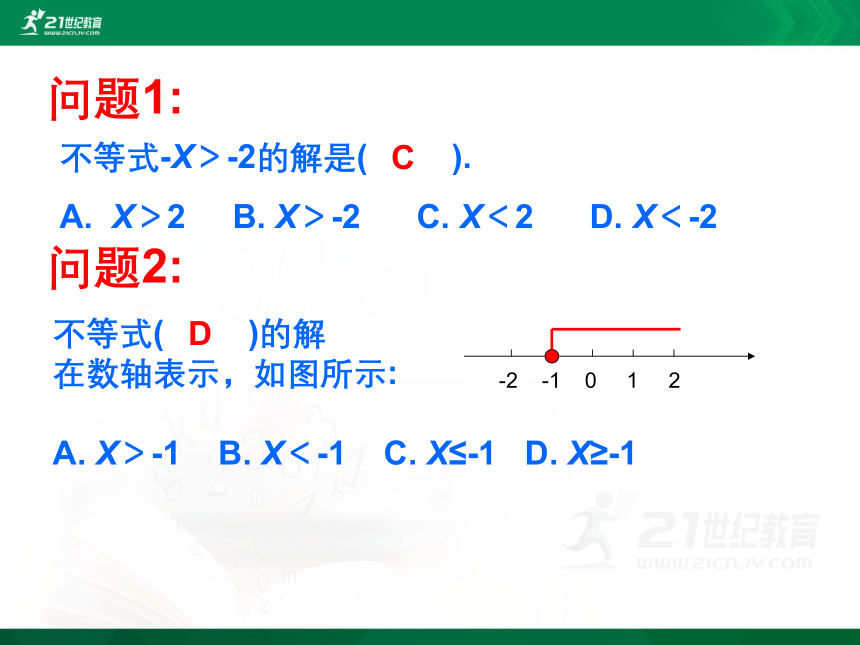
问题1:
不等式-X>-2的解是( ).
A. X>2 B. X>-2 C. X<2 D. X<-2
问题2:
C
不等式( )的解
在数轴表示,如图所示:
A. X>-1 B. X<-1 C. X≤-1 D. X≥-1
-2 -1 0 1 2
D
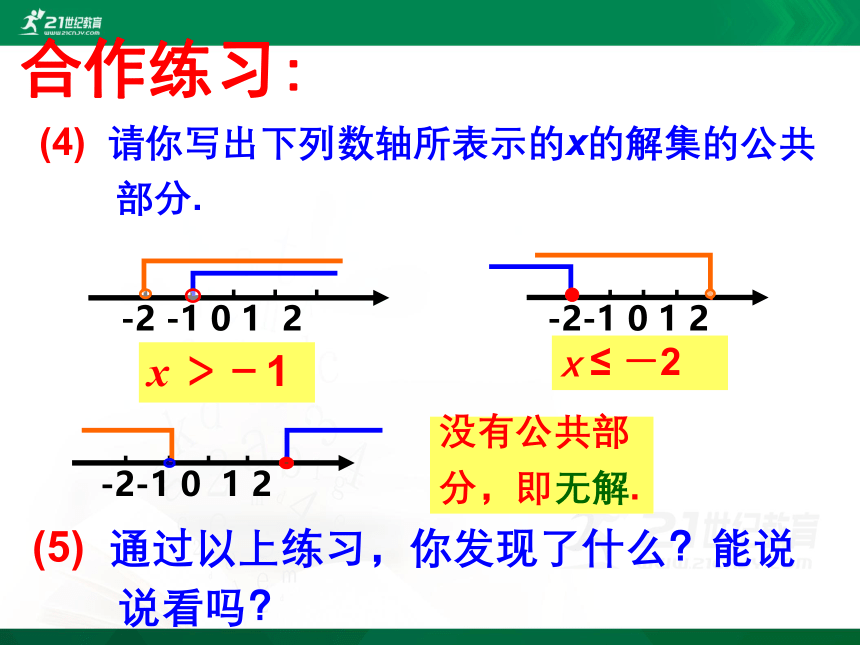
合作练习:
① X>-1 ; ② X≤2
(1) 用数轴表示下列不等式的值:
(2) 在同一数轴上表示出上列两个不等式
的值:
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
(3) 你能写出第(2)小题中数轴所表示的x
的解集的公共部分吗?
-1合作练习:
(4) 请你写出下列数轴所表示的x的解集的公共
部分.
-2 -1 0 1 2
x >-1
-2-1 0 1 2
x ≤ -2
-2-1 0 1 2
没有公共部
分,即无解.
(5) 通过以上练习,你发现了什么?能说
说看吗?
(用数轴来解释)
定义:
组成不等式组的各个不等式的解的公共部分就是不等式组的解.
注: 当它们没有公共部分时,
则称这个不等式组无解.
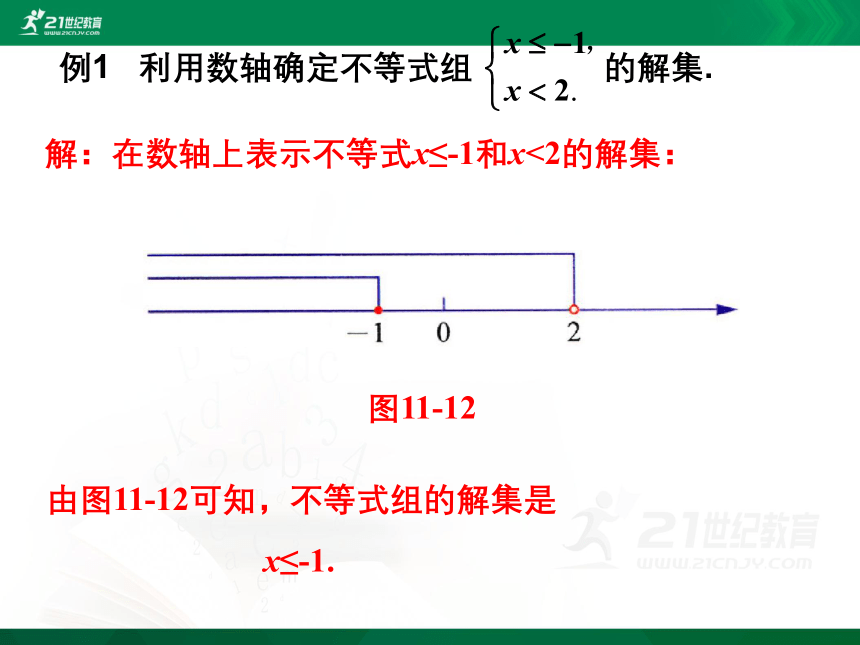
例1 利用数轴确定不等式组 的解集.
解:在数轴上表示不等式x≤-1和x<2的解集:
由图11-12可知,不等式组的解集是
x≤-1.
图11-12
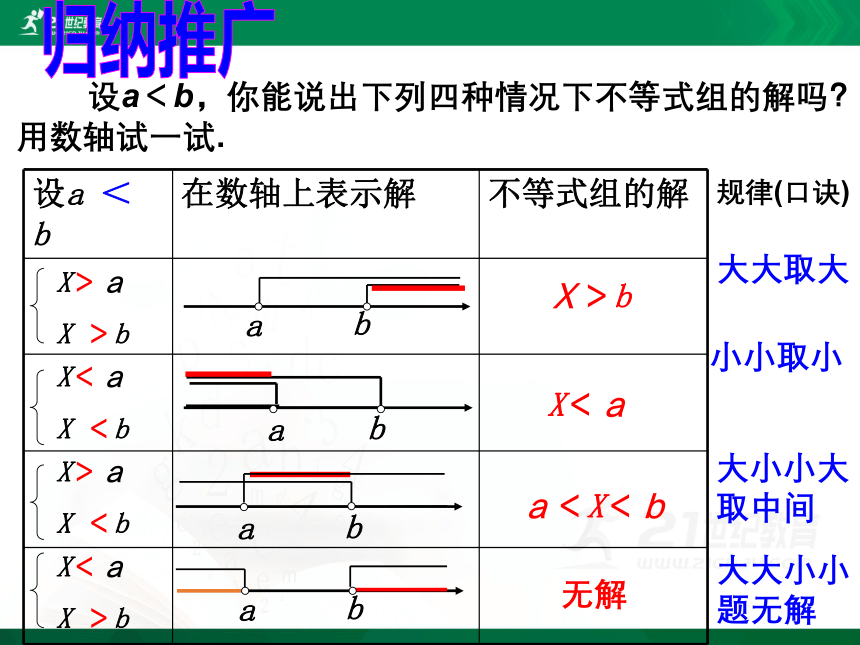
设a<b,你能说出下列四种情况下不等式组的解吗?用数轴试一试.
设a < b
在数轴上表示解
不等式组的解
X>a
X >b
X<a
X <b
X>a
X <b
X<a
X >b
a
b
a
b
a
b
a
b
X>b
X<a
无解
a<X<b
大小小大取中间
大大小小题无解
小小取小
大大取大
规律(口诀)
归纳推广
求下列不等式组的解
①
x ≥ -1
x≥ 2
x≥ 2
②
x< -1
x< 2
x< -1
无解
③
x ≥ -1
x< 2
-1≤ x< 2
x< -1
④
x≥ 2
比一比
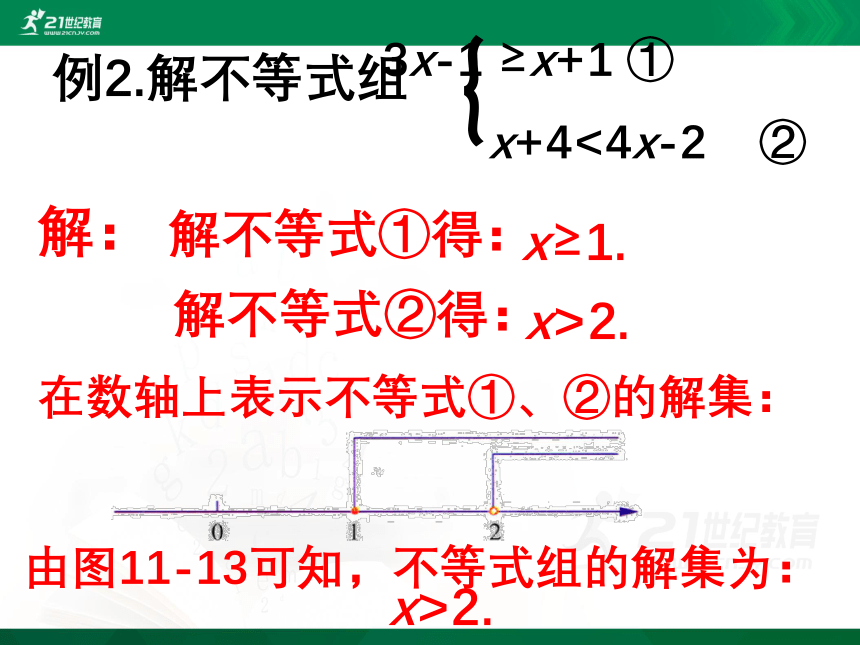
3x-1 ≥x+1 ①
x+4<4x-2 ②
{
解不等式①得:
x≥1.
解不等式②得:
x>2.
在数轴上表示不等式①、②的解集:
例2.解不等式组
解:
由图11-13可知,不等式组的解集为:
x>2.
例3.解不等式组:
①
②
解:解不等式①,得
解不等式②,得
在数轴上表示不等式①、②的解集:
由图11-14可知,不等式①、②的解集没有公共部分,不等式组无解.
2x-1>x+1
x+8<4x-1
解不等式组
①
②
解:解不等式①,得 x>2.
解不等式② ,得 x>3.
在数轴上表示不等式①, ②的解
所以这个不等式组的解是 x>3
基本步骤:
(1)分别求出各不等式的解
(2)将它们的解表示在同一数轴上
(3)写出原不等式组的解(即为它们解的公共部分).
2
1
3
0
例:某工厂用如图所示的长方形和正方形纸板,糊横式与竖式两种无盖的长方体包装盒,如图.现有长方形纸板351张,正方形纸板151张,要糊的两种包装盒品的总数为100个.若按两种包装盒的生产个数分,问有几种生产方案?如果从原材料的利用率考虑,你认为应选择哪一种方案?
横式无盖
竖式无盖
和列方程解应用题一样,当数量关系比较复杂时,我们可以通过列表来分析:
x
100-x
3x
(张)
(张)
4(100-x)
2x
100-x
合计(张)
现有纸板(张)
3x+4(100-x)
2x+100-x
351
151
解:设生产横式无盖的长方体包装盒x个,则生产竖式无 盖的长方体包装盒(100-x)个.由题意得:
化简,得:
解这个不等式,得49≤x≤51.
因为x是整数,所以x=49或x=50或x=51.
当x=49时,400-x=351,100+x=149,长方形纸板恰好用完,正方形纸板剩2张;
当x=50时,400-x=350,100+x=150,长方形、正方形纸板各剩1张;
当x=51时,400-x=349,100+x=151,长方形纸板剩2张,正方形纸板恰好用完.
由于长方形纸板的面积大于正方形纸板的面积,所以当x=49时,原材料的利用率最高.
答:一共有三种方案(1)横式的包装盒生产49个,竖式的生产51个;(2)横式的和竖式的包装盒各生产50个;(3)横式的包装盒生产51个,竖式的包装盒生产49个.第(1)种方案原材料的利用率最高.
加油!
练习: 三角形三边长分别为4,a+1,7,
则a的取值范围是 .
2<a <10
友情提示:
两边之差 < 第三边< 两边之和
加油!
1. 不等式组 的解集是( ).
2x > -4
ì
í
?
x-5≤0
A. X>-2
B. -2 < X ≤ 5
C. X ≤ 5
D. 无解
B
加油!
2. 不等式组 的整数解是( ).
x +1≥0
ì
í
?
x+2 < 3
A. -1,0,1
B. -1,1
C. -1,0
D. 0,1
C
加油!
0
1
2
3
-1
m
思考题
若不等式组 的解是x>2,
则m的取值范围是 .
x >m
x >2
{
m≤2
说一说不等式组的解集有哪几种情况?
同大取大: x≥a,x≥b,且a>b,解集为: x≥a.
同小取小: x≤a,x≤b,且a>b,解集为: x≤b.
大于小的小于大的取中间: x≤a,x≥b,且a>b,解集为: b≤x≤a.
大于大的小于小的是空集: x ≥a,x ≤b,且a>b,解集为:空集.
假设a解集为: x >b
解集为: x<a
解集为:a<x <b
解集为:空集
1.说出下列不等式组的解集:
﹣3
﹣2
﹣1
0
1
2
3
由图可知,原不等式组的解集是x>0.
﹣3
﹣1
0
1
﹣2
﹣5
﹣4
由图可知,原不等式组的解集是x<-5.
﹣1
0
1
2
3
4
5
6
7
由图可知,原不等式组的解集是2由图可知,原不等式组无解.
﹣3
2
﹣1
0
1
﹣2
3
2.解下列不等式组,并把解集在数轴上表示出来:
①
②
解
﹣3
﹣2
﹣1
0
1
2
3
①
②
解
﹣2
﹣1
0
1
2
3.解不等式组:
①
②
解:解不等式①,得
解不等式②,得
x+3<5,
x-2>4.
x>6
x<2
在同一数轴上表示不等式①②的解集:
因此,不存在实数x,使得x+3<5,且x-2>4.
2
4
6
0
8
10
1.解下列不等式组,并把解集在数轴上表示出来:
①
②
解
﹣1
0
1
2
3
﹣3
﹣2
①
②
解
﹣1
0
1
2
3
4
5
6
7
①
②
解
﹣1
0
1
2
3
﹣4
﹣3
﹣2
2.解本节开始的问题1,2中得到的不等式组:
①
②
解
﹣2
﹣1
0
1
2
①
②
解
﹣12324
0
12324
1、解下列 不等式组:
①
②
解:解不等式①,得
解不等式②,得
2x-4<0,
3x +12>0;
x>-4.
x<2.
(1)
解集为
-4<x<2.
①
②
解:解不等式①,得
解不等式②,得
x-2≥- 5,
9-6x > 8;
x≥-3.
(2)
解集为
x< .
-3≤x< .
2、已知4a+5和2a-4的值都是正数,求a得取值范围.
解:由题意得: ① 4a+5>0,
② 2a-4 >0 .
解不等式①,得 ,
解不等式②,得 a>2,
a得取值范围
a>2.
这节课你有什么收获啊?
请你用自己的话谈谈体会!
1、一元一次不等式组
2、不等式组的解
3、解一元一次不等式组和解的四种情况.
谢谢聆听
11.6 一元一次不等式组
第11章 一元一次不等式
2020-2021学年度苏科版七年级下册
喜羊羊:“懒羊羊,你怎么减肥了?”
懒羊羊:“是的,我的体重由一个月前的18kg降到现在的15kg.”
喜羊羊:“是吗?我现在的体重再加上2kg的话就超过你了,但没超过你原来的体重.”
设喜羊羊现在的体重为 x (kg), 你能列出几个不等式?
由几个同一未知数的一元一次不等式所组成的一组不等式, 叫做一元一次不等式组.
一元一次不等式组
例如
辩一辩
下列式子中,哪些是一元一次不等式组?
不是
不是
√
√
√
√
不是
问题1:
不等式-X>-2的解是( ).
A. X>2 B. X>-2 C. X<2 D. X<-2
问题2:
C
不等式( )的解
在数轴表示,如图所示:
A. X>-1 B. X<-1 C. X≤-1 D. X≥-1
-2 -1 0 1 2
D
合作练习:
① X>-1 ; ② X≤2
(1) 用数轴表示下列不等式的值:
(2) 在同一数轴上表示出上列两个不等式
的值:
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
(3) 你能写出第(2)小题中数轴所表示的x
的解集的公共部分吗?
-1
(4) 请你写出下列数轴所表示的x的解集的公共
部分.
-2 -1 0 1 2
x >-1
-2-1 0 1 2
x ≤ -2
-2-1 0 1 2
没有公共部
分,即无解.
(5) 通过以上练习,你发现了什么?能说
说看吗?
(用数轴来解释)
定义:
组成不等式组的各个不等式的解的公共部分就是不等式组的解.
注: 当它们没有公共部分时,
则称这个不等式组无解.
例1 利用数轴确定不等式组 的解集.
解:在数轴上表示不等式x≤-1和x<2的解集:
由图11-12可知,不等式组的解集是
x≤-1.
图11-12
设a<b,你能说出下列四种情况下不等式组的解吗?用数轴试一试.
设a < b
在数轴上表示解
不等式组的解
X>a
X >b
X<a
X <b
X>a
X <b
X<a
X >b
a
b
a
b
a
b
a
b
X>b
X<a
无解
a<X<b
大小小大取中间
大大小小题无解
小小取小
大大取大
规律(口诀)
归纳推广
求下列不等式组的解
①
x ≥ -1
x≥ 2
x≥ 2
②
x< -1
x< 2
x< -1
无解
③
x ≥ -1
x< 2
-1≤ x< 2
x< -1
④
x≥ 2
比一比
3x-1 ≥x+1 ①
x+4<4x-2 ②
{
解不等式①得:
x≥1.
解不等式②得:
x>2.
在数轴上表示不等式①、②的解集:
例2.解不等式组
解:
由图11-13可知,不等式组的解集为:
x>2.
例3.解不等式组:
①
②
解:解不等式①,得
解不等式②,得
在数轴上表示不等式①、②的解集:
由图11-14可知,不等式①、②的解集没有公共部分,不等式组无解.
2x-1>x+1
x+8<4x-1
解不等式组
①
②
解:解不等式①,得 x>2.
解不等式② ,得 x>3.
在数轴上表示不等式①, ②的解
所以这个不等式组的解是 x>3
基本步骤:
(1)分别求出各不等式的解
(2)将它们的解表示在同一数轴上
(3)写出原不等式组的解(即为它们解的公共部分).
2
1
3
0
例:某工厂用如图所示的长方形和正方形纸板,糊横式与竖式两种无盖的长方体包装盒,如图.现有长方形纸板351张,正方形纸板151张,要糊的两种包装盒品的总数为100个.若按两种包装盒的生产个数分,问有几种生产方案?如果从原材料的利用率考虑,你认为应选择哪一种方案?
横式无盖
竖式无盖
和列方程解应用题一样,当数量关系比较复杂时,我们可以通过列表来分析:
x
100-x
3x
(张)
(张)
4(100-x)
2x
100-x
合计(张)
现有纸板(张)
3x+4(100-x)
2x+100-x
351
151
解:设生产横式无盖的长方体包装盒x个,则生产竖式无 盖的长方体包装盒(100-x)个.由题意得:
化简,得:
解这个不等式,得49≤x≤51.
因为x是整数,所以x=49或x=50或x=51.
当x=49时,400-x=351,100+x=149,长方形纸板恰好用完,正方形纸板剩2张;
当x=50时,400-x=350,100+x=150,长方形、正方形纸板各剩1张;
当x=51时,400-x=349,100+x=151,长方形纸板剩2张,正方形纸板恰好用完.
由于长方形纸板的面积大于正方形纸板的面积,所以当x=49时,原材料的利用率最高.
答:一共有三种方案(1)横式的包装盒生产49个,竖式的生产51个;(2)横式的和竖式的包装盒各生产50个;(3)横式的包装盒生产51个,竖式的包装盒生产49个.第(1)种方案原材料的利用率最高.
加油!
练习: 三角形三边长分别为4,a+1,7,
则a的取值范围是 .
2<a <10
友情提示:
两边之差 < 第三边< 两边之和
加油!
1. 不等式组 的解集是( ).
2x > -4
ì
í
?
x-5≤0
A. X>-2
B. -2 < X ≤ 5
C. X ≤ 5
D. 无解
B
加油!
2. 不等式组 的整数解是( ).
x +1≥0
ì
í
?
x+2 < 3
A. -1,0,1
B. -1,1
C. -1,0
D. 0,1
C
加油!
0
1
2
3
-1
m
思考题
若不等式组 的解是x>2,
则m的取值范围是 .
x >m
x >2
{
m≤2
说一说不等式组的解集有哪几种情况?
同大取大: x≥a,x≥b,且a>b,解集为: x≥a.
同小取小: x≤a,x≤b,且a>b,解集为: x≤b.
大于小的小于大的取中间: x≤a,x≥b,且a>b,解集为: b≤x≤a.
大于大的小于小的是空集: x ≥a,x ≤b,且a>b,解集为:空集.
假设a
解集为: x<a
解集为:a<x <b
解集为:空集
1.说出下列不等式组的解集:
﹣3
﹣2
﹣1
0
1
2
3
由图可知,原不等式组的解集是x>0.
﹣3
﹣1
0
1
﹣2
﹣5
﹣4
由图可知,原不等式组的解集是x<-5.
﹣1
0
1
2
3
4
5
6
7
由图可知,原不等式组的解集是2
﹣3
2
﹣1
0
1
﹣2
3
2.解下列不等式组,并把解集在数轴上表示出来:
①
②
解
﹣3
﹣2
﹣1
0
1
2
3
①
②
解
﹣2
﹣1
0
1
2
3.解不等式组:
①
②
解:解不等式①,得
解不等式②,得
x+3<5,
x-2>4.
x>6
x<2
在同一数轴上表示不等式①②的解集:
因此,不存在实数x,使得x+3<5,且x-2>4.
2
4
6
0
8
10
1.解下列不等式组,并把解集在数轴上表示出来:
①
②
解
﹣1
0
1
2
3
﹣3
﹣2
①
②
解
﹣1
0
1
2
3
4
5
6
7
①
②
解
﹣1
0
1
2
3
﹣4
﹣3
﹣2
2.解本节开始的问题1,2中得到的不等式组:
①
②
解
﹣2
﹣1
0
1
2
①
②
解
﹣12324
0
12324
1、解下列 不等式组:
①
②
解:解不等式①,得
解不等式②,得
2x-4<0,
3x +12>0;
x>-4.
x<2.
(1)
解集为
-4<x<2.
①
②
解:解不等式①,得
解不等式②,得
x-2≥- 5,
9-6x > 8;
x≥-3.
(2)
解集为
x< .
-3≤x< .
2、已知4a+5和2a-4的值都是正数,求a得取值范围.
解:由题意得: ① 4a+5>0,
② 2a-4 >0 .
解不等式①,得 ,
解不等式②,得 a>2,
a得取值范围
a>2.
这节课你有什么收获啊?
请你用自己的话谈谈体会!
1、一元一次不等式组
2、不等式组的解
3、解一元一次不等式组和解的四种情况.
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
