12.1 定义与命题(第1课时) 课件(共26张PPT)
文档属性
| 名称 | 12.1 定义与命题(第1课时) 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 18:34:15 | ||
图片预览








文档简介
第1课时
12.1 定义与命题
第12章 证明
2020-2021学年度苏科版七年级下册
想一想
?
例如:
“具有中华人民共和国国籍的人,叫做中华人民共和国公民” 是“中华人民共和国公民”的定义;
“两点之间 线段的长度,叫做这两点之间的距离” 是“两点之间的距离”的定义;
“两组对边分别平行的四边形叫做平行四边形” 是“平行四边形”的定义;
你还能举出曾学过的“定义”吗?
什么是定义?
对名称和术语的含义加以描述,作出明确的规定,也就是给出它们的定义.
例如:
(1)“具有中华人民共和国国籍的人,叫做中华人民共和国公民”是“中华人民共和国公民”的定义
(2)“两点之间线段的长度,叫做这两点之间的距离”是“两点之间距离”的定义
(3)“无限不循环小数称为无理数”是“无理数”的定义
你还能举出曾学过的“定义”吗?
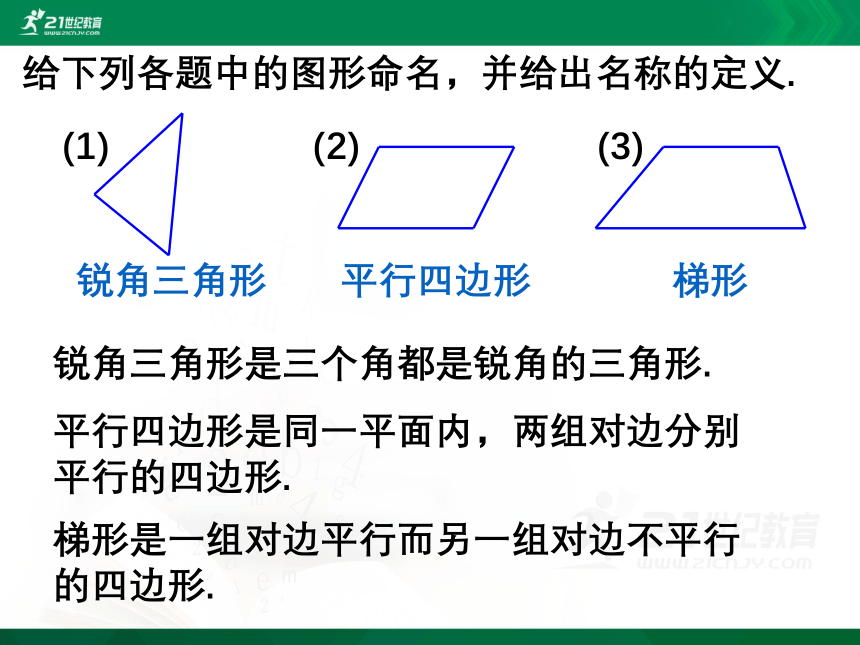
给下列各题中的图形命名,并给出名称的定义.
锐角三角形
平行四边形
梯形
锐角三角形是三个角都是锐角的三角形.
平行四边形是同一平面内,两组对边分别平行的四边形.
梯形是一组对边平行而另一组对边不平行的四边形.
(1)
(2)
(3)
什么是命题?
判断一件事情的句子,叫做命题.
例如:
(1)任何一个三角形一定有直角.
(2)对顶角相等.
(3)无论n为怎样的自然数,式子n2-n+11的值都是质数.
(4)如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
命题
反之,如果一个句子没有对某一件事情作出任何判断,那么它就不是命题.
例如:
(1)你喜欢数学吗?
(2)做线段AB=CD
下列句子中,哪些是命题,哪些不是命题?
(1)正数大于一切负数吗?
(2)两点之间线段最短.
(4)作一条直线和一直直线垂直.
(3) 不是无理数.
不是命题
是命题
是命题
不是命题
观察下列命题,试找出命题的共同的结构特征
(1)如果一个三角形是等腰三角形,那么这个三角形的两个底角 相等;
(2)如果a=b,那么a2=b2;
(3)如果两个三角形的三条边对应相等,那么这两个三角形全等.
寻找命题的“共同的结构特征”
1、每个命题都由条件和结论两部分组成.条件是已知
事项,结论是由已事项推断出的事项.
2、一般地,命题可以写成“如果……,那么……”的形式,
其中“如果”引出的部分是条件,“那么”引出的部分是结论.
要说明一个命题是假命题,通常可以举出一个例子,使之具备命题的条件,而不具备命题的结论,这种例子称为反例.
1.下列命题的条件是什么?结论是什么?
(2)如果a≠b,b≠c,那么a≠c;
(1)如果两个角相等,那么它们是对顶角;
(3)全等三角形的面积相等;
(4)菱形的四条边都相等.
2.上述的命题中,哪些是正确的?哪些是不正确的?你怎么知道它们是不正确的?与同伴交流.
正确的命题称为真命题,不正确的的命题称为假命题.
做一做
把命题“在一个三角形中,等角对等边”改写成:“如果…那么…” 的形式,并分别指出命题的题设和结论.
解:这个命题可以改写成:
“如果在一个三角形中有两个角相等,那么这两个角所对的边也相等”.
这里的题设是“在一个三角形中有两个角相等”,结论是“这两个角所对的边也相等”.
说明命题“一个锐角与一个钝角的和等于一个平角”是假命题.
只需举出一个反例(某一锐角与某一钝角的和不是180°).
如:一个锐角30°与一个钝角100°的和等于130°,还是钝角,不是平角.
分析:
把下列命题改为“如果……,那么……”的形式,并分别指出它们的条件和结论:
(1)全等三角形的对应边相等;
(2)在同一平面内,垂直与同一条直线的两条
直线互相平行.
解:(1)如果两个三角形全等,那么它们的对
应边相等;
(2)在同一平面内,如果两条
直线垂直与同一条直线,
那么这两条直线互相平行.
指出下列命题中的真命题和假命题:
(1)同位角相等,两直线平行;
(2)多边形的内角和等于180°;
(3)三角形的外角和等于360°;
(4)平行与同一条直线的两条直线互相平行.
(1)、(3)、(4)
真命题:
假命题:
(2)
在四边形ABCD中,给出下列论断:1.AB∥DC;2.AD=BC;3.∠A=∠C.以其中两个作为条件,另外一个作为结论,用“如果…那么…”的形式,写出一个你认为正确的命题.
解:如果AB∥DC,∠A=∠C
那么AD=BC.
1.将下列命题写成“如果……那么……”的形式,分别说出它的条件和结论,并指出它是真命题还是假命题:
如果同一平面内两条直线垂直于同一直线,
那么这两条直线平行.
条件是:
结论是:
改写成:
同一平面内两条直线垂直于同一直线.
两条直线平行.
(1) 在同一平面内,垂直于同一直线的两条直线平行;
(2)两个锐角的和是钝角;
如果两个角是锐角,那么两个角的和是钝角.
条件是:
结论是:
改写成:
两个角是锐角.
两个角的和是钝角.
真命题
假命题
(3)同旁内角互补,两直线平行;
(4)负数小于0.
如果同旁内角互补,那么两直线平行.
条件是:
结论是:
改写成:
同旁内角互补.
两直线平行.
真命题
如果一个数是负数,那么这个数小于0.
条件是:
结论是:
改写成:
一个数是负数.
这个数小于0.
真命题
两个多边形全等不仅与长度有关,还与多边形的角度有关,如:边长相等的菱形与正方形不全等.
2.下列命题中哪些是假命题?为什么?
(1)如果 ,那么 ;
结论应该为 .
(2)各边分别相等的两个多边形一定全等;
假命题.
假命题.
(3)如果a≠0,b≠0,那么a2+ab+b2 = (a+b)2
如:a=1,b=1时a2+ab+b2 =3, (a+b)?=4,
这时a2+ab+b2≠ (a+b)2,所以这个命题是假命题.
假命题.
1.下列各命题的条件是什么?结论是什么?
(1)如果a<0,b<0,那么a+b<0;
(2)如果n<1,那么n2-1<0;
(3)同角的补角相等;
(4)直角都相等.
(1)条件:如果a<0,b<0,结论:那么a+b<0.
(2)条件:如果n<1,结论:那么n2-1<0.
(3)条件:同角的补角,结论:两个角相等.
(4)条件:直角,结论:所有的直角都相等.
2.在第一题的命题中,哪些是真命题?哪些是假命题?
(1)真命题;
(2)假命题;
(3)真命题;
(4)真命题.
下列句子中,哪些是命题?哪些不是命题?
(1)对顶角相等;
(2)画一个角等于已知角;
(3)两直线平行,同位角相等;
(4)a、b两条直线平行吗?
(5)若a2=4,求a的值.
(6)若a2= b2,则a=b.
不是
是
不是
不是
是
是
请你当判官
1、定义:对名称和术语的含义加以描述,作出明确的规定,也就是给出它们的定义 .
2、命题的定义:判断一件事情的句子,叫做命题.
3、命题的结构:每个命题都由条件和结论两部分组成.条件是已知事项,结论是由已事项推断出的事项.
4、命题的特征:一般地,命题可以写成“如果……,那么……”的形式,其中“如果”引出的部分是条件,“那么”引出的部分是结论.
5、命题的分类:真命题和假命题(判断就是命题).
小结 拓展
结束寄语
命题是几何学习中最基础的概念.
定义是反映事物本质意义的描述性语句.
谢谢聆听
12.1 定义与命题
第12章 证明
2020-2021学年度苏科版七年级下册
想一想
?
例如:
“具有中华人民共和国国籍的人,叫做中华人民共和国公民” 是“中华人民共和国公民”的定义;
“两点之间 线段的长度,叫做这两点之间的距离” 是“两点之间的距离”的定义;
“两组对边分别平行的四边形叫做平行四边形” 是“平行四边形”的定义;
你还能举出曾学过的“定义”吗?
什么是定义?
对名称和术语的含义加以描述,作出明确的规定,也就是给出它们的定义.
例如:
(1)“具有中华人民共和国国籍的人,叫做中华人民共和国公民”是“中华人民共和国公民”的定义
(2)“两点之间线段的长度,叫做这两点之间的距离”是“两点之间距离”的定义
(3)“无限不循环小数称为无理数”是“无理数”的定义
你还能举出曾学过的“定义”吗?
给下列各题中的图形命名,并给出名称的定义.
锐角三角形
平行四边形
梯形
锐角三角形是三个角都是锐角的三角形.
平行四边形是同一平面内,两组对边分别平行的四边形.
梯形是一组对边平行而另一组对边不平行的四边形.
(1)
(2)
(3)
什么是命题?
判断一件事情的句子,叫做命题.
例如:
(1)任何一个三角形一定有直角.
(2)对顶角相等.
(3)无论n为怎样的自然数,式子n2-n+11的值都是质数.
(4)如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
命题
反之,如果一个句子没有对某一件事情作出任何判断,那么它就不是命题.
例如:
(1)你喜欢数学吗?
(2)做线段AB=CD
下列句子中,哪些是命题,哪些不是命题?
(1)正数大于一切负数吗?
(2)两点之间线段最短.
(4)作一条直线和一直直线垂直.
(3) 不是无理数.
不是命题
是命题
是命题
不是命题
观察下列命题,试找出命题的共同的结构特征
(1)如果一个三角形是等腰三角形,那么这个三角形的两个底角 相等;
(2)如果a=b,那么a2=b2;
(3)如果两个三角形的三条边对应相等,那么这两个三角形全等.
寻找命题的“共同的结构特征”
1、每个命题都由条件和结论两部分组成.条件是已知
事项,结论是由已事项推断出的事项.
2、一般地,命题可以写成“如果……,那么……”的形式,
其中“如果”引出的部分是条件,“那么”引出的部分是结论.
要说明一个命题是假命题,通常可以举出一个例子,使之具备命题的条件,而不具备命题的结论,这种例子称为反例.
1.下列命题的条件是什么?结论是什么?
(2)如果a≠b,b≠c,那么a≠c;
(1)如果两个角相等,那么它们是对顶角;
(3)全等三角形的面积相等;
(4)菱形的四条边都相等.
2.上述的命题中,哪些是正确的?哪些是不正确的?你怎么知道它们是不正确的?与同伴交流.
正确的命题称为真命题,不正确的的命题称为假命题.
做一做
把命题“在一个三角形中,等角对等边”改写成:“如果…那么…” 的形式,并分别指出命题的题设和结论.
解:这个命题可以改写成:
“如果在一个三角形中有两个角相等,那么这两个角所对的边也相等”.
这里的题设是“在一个三角形中有两个角相等”,结论是“这两个角所对的边也相等”.
说明命题“一个锐角与一个钝角的和等于一个平角”是假命题.
只需举出一个反例(某一锐角与某一钝角的和不是180°).
如:一个锐角30°与一个钝角100°的和等于130°,还是钝角,不是平角.
分析:
把下列命题改为“如果……,那么……”的形式,并分别指出它们的条件和结论:
(1)全等三角形的对应边相等;
(2)在同一平面内,垂直与同一条直线的两条
直线互相平行.
解:(1)如果两个三角形全等,那么它们的对
应边相等;
(2)在同一平面内,如果两条
直线垂直与同一条直线,
那么这两条直线互相平行.
指出下列命题中的真命题和假命题:
(1)同位角相等,两直线平行;
(2)多边形的内角和等于180°;
(3)三角形的外角和等于360°;
(4)平行与同一条直线的两条直线互相平行.
(1)、(3)、(4)
真命题:
假命题:
(2)
在四边形ABCD中,给出下列论断:1.AB∥DC;2.AD=BC;3.∠A=∠C.以其中两个作为条件,另外一个作为结论,用“如果…那么…”的形式,写出一个你认为正确的命题.
解:如果AB∥DC,∠A=∠C
那么AD=BC.
1.将下列命题写成“如果……那么……”的形式,分别说出它的条件和结论,并指出它是真命题还是假命题:
如果同一平面内两条直线垂直于同一直线,
那么这两条直线平行.
条件是:
结论是:
改写成:
同一平面内两条直线垂直于同一直线.
两条直线平行.
(1) 在同一平面内,垂直于同一直线的两条直线平行;
(2)两个锐角的和是钝角;
如果两个角是锐角,那么两个角的和是钝角.
条件是:
结论是:
改写成:
两个角是锐角.
两个角的和是钝角.
真命题
假命题
(3)同旁内角互补,两直线平行;
(4)负数小于0.
如果同旁内角互补,那么两直线平行.
条件是:
结论是:
改写成:
同旁内角互补.
两直线平行.
真命题
如果一个数是负数,那么这个数小于0.
条件是:
结论是:
改写成:
一个数是负数.
这个数小于0.
真命题
两个多边形全等不仅与长度有关,还与多边形的角度有关,如:边长相等的菱形与正方形不全等.
2.下列命题中哪些是假命题?为什么?
(1)如果 ,那么 ;
结论应该为 .
(2)各边分别相等的两个多边形一定全等;
假命题.
假命题.
(3)如果a≠0,b≠0,那么a2+ab+b2 = (a+b)2
如:a=1,b=1时a2+ab+b2 =3, (a+b)?=4,
这时a2+ab+b2≠ (a+b)2,所以这个命题是假命题.
假命题.
1.下列各命题的条件是什么?结论是什么?
(1)如果a<0,b<0,那么a+b<0;
(2)如果n<1,那么n2-1<0;
(3)同角的补角相等;
(4)直角都相等.
(1)条件:如果a<0,b<0,结论:那么a+b<0.
(2)条件:如果n<1,结论:那么n2-1<0.
(3)条件:同角的补角,结论:两个角相等.
(4)条件:直角,结论:所有的直角都相等.
2.在第一题的命题中,哪些是真命题?哪些是假命题?
(1)真命题;
(2)假命题;
(3)真命题;
(4)真命题.
下列句子中,哪些是命题?哪些不是命题?
(1)对顶角相等;
(2)画一个角等于已知角;
(3)两直线平行,同位角相等;
(4)a、b两条直线平行吗?
(5)若a2=4,求a的值.
(6)若a2= b2,则a=b.
不是
是
不是
不是
是
是
请你当判官
1、定义:对名称和术语的含义加以描述,作出明确的规定,也就是给出它们的定义 .
2、命题的定义:判断一件事情的句子,叫做命题.
3、命题的结构:每个命题都由条件和结论两部分组成.条件是已知事项,结论是由已事项推断出的事项.
4、命题的特征:一般地,命题可以写成“如果……,那么……”的形式,其中“如果”引出的部分是条件,“那么”引出的部分是结论.
5、命题的分类:真命题和假命题(判断就是命题).
小结 拓展
结束寄语
命题是几何学习中最基础的概念.
定义是反映事物本质意义的描述性语句.
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
