12.2 证明(第1课时) 课件(共44张PPT)
文档属性
| 名称 | 12.2 证明(第1课时) 课件(共44张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 18:44:20 | ||
图片预览







文档简介
第1课时
12.2 证明
第12章 证明
2020-2021学年度苏科版七年级下册
欣赏判断
观察图片,蓝色的粗线是直的吗?
观察图形,一组直线a,b,c,d是否都互相平行?
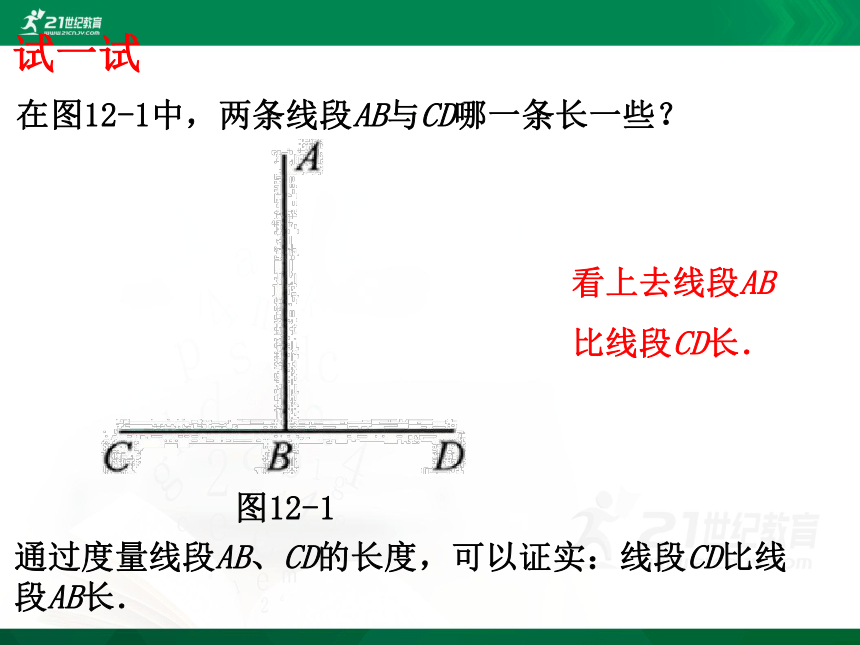
在图12-1中,两条线段AB与CD哪一条长一些?
图12-1
看上去线段AB比线段CD长.
通过度量线段AB、CD的长度,可以证实:线段CD比线段AB长.
试一试
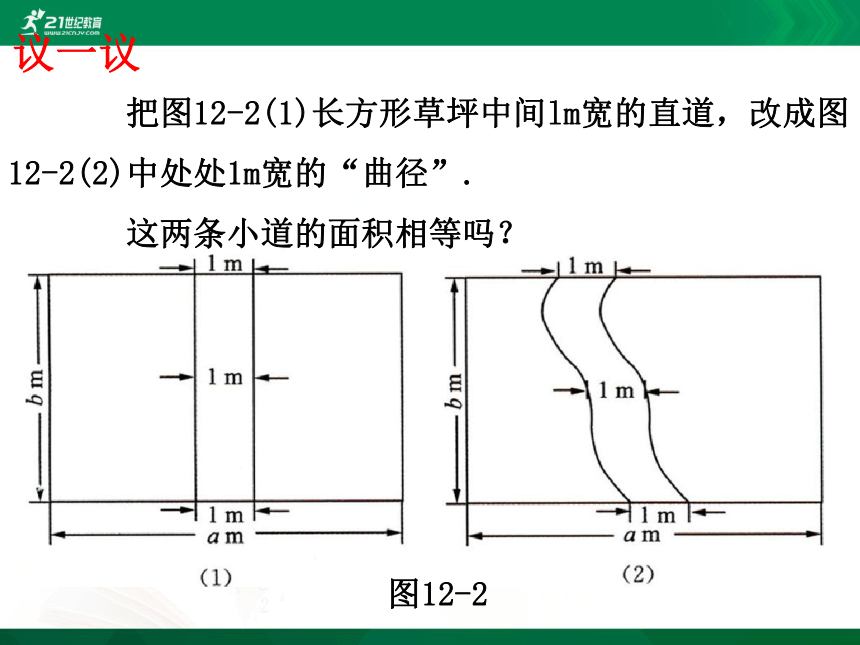
把图12-2(1)长方形草坪中间lm宽的直道,改成图12-2(2)中处处1m宽的“曲径”.
这两条小道的面积相等吗?
议一议
图12-2
如果将图12-2(2)中小道左边的草坪
向右平移1m,那么得到一个长为(a-1)m、宽为bm的长方形(如图12-3),它的面积为b(a-1)m2.
于是,“曲径”的面积为ab-b(a-1)=
ab-ab+b=b(m2).
由图12-2(1)可知直道的面积为
1×b=b(m2).
通过图形的平移和计算,可以证实:两条小道的面积等.
图12-3
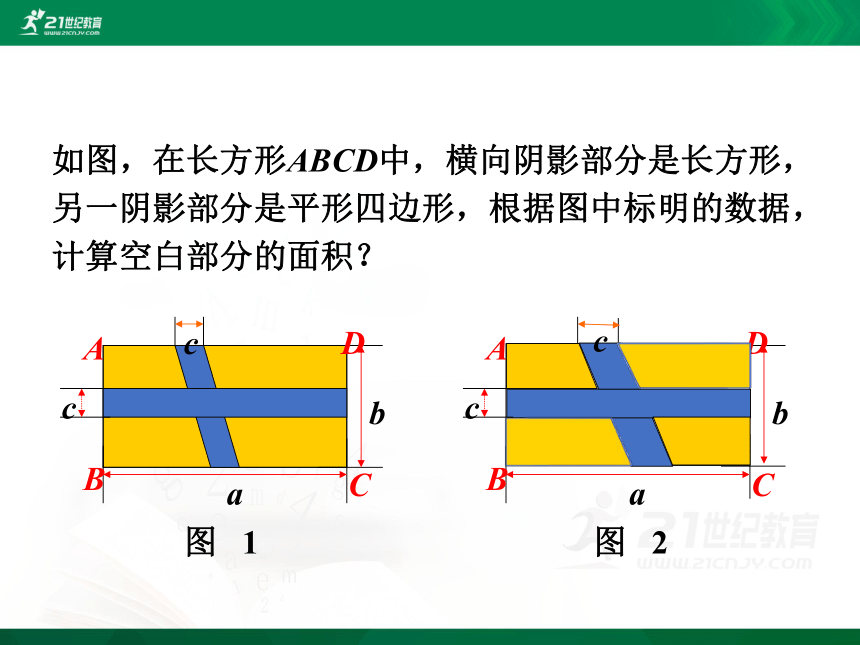
如图,在长方形ABCD中,横向阴影部分是长方形,另一阴影部分是平形四边形,根据图中标明的数据,计算空白部分的面积?
c
c
a
b
A
C
D
B
c
c
a
b
A
C
D
B
图 1
图 2
点拔:这里通过平移,避免了对图形分别计算面积,
使求解简洁方便.
析解:利用“平移不改变图形的形状与大小”这一性质可以迅速解决本题.由图可知,四个空白四边形经过平移可以组成一个长方形,它的长为(a-c),宽为(b-c),所以空白部分的面积为:(a-c)(b-c)=ab-ac-bc+c2
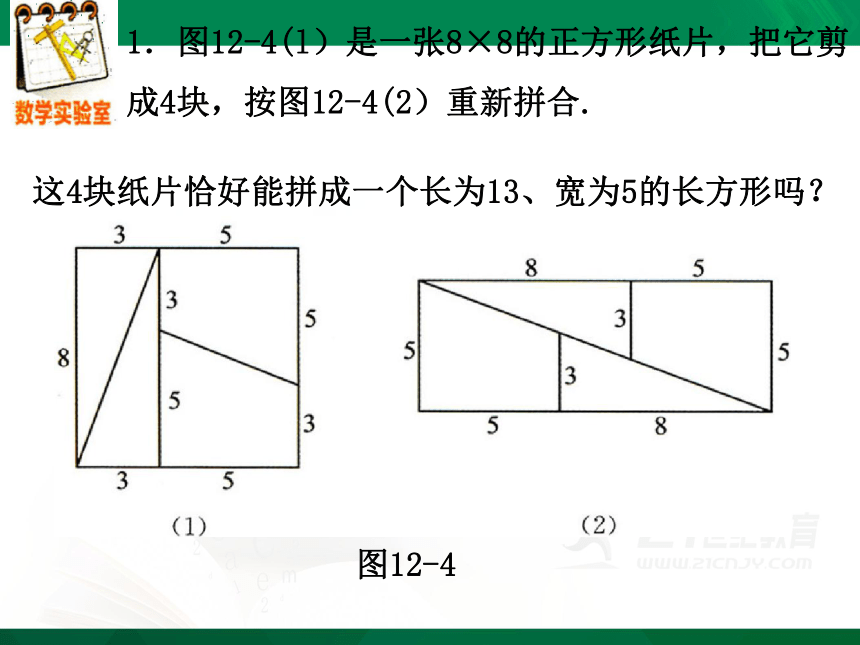
1.图12-4(l)是一张8×8的正方形纸片,把它剪成4块,按图12-4(2)重新拼合.
这4块纸片恰好能拼成一个长为13、宽为5的长方形吗?
图12-4
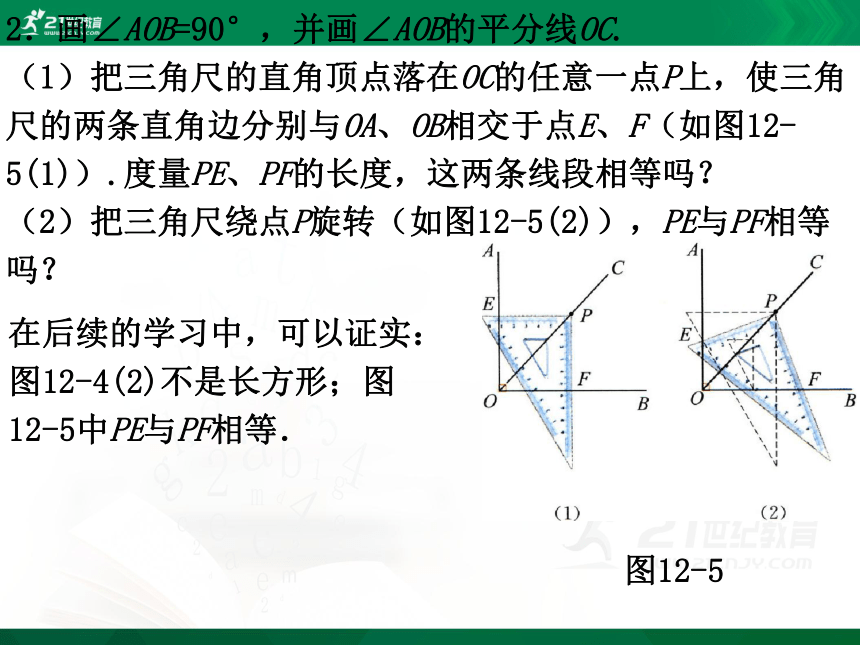
2.画∠AOB=90°,并画∠AOB的平分线OC.
(1)把三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边分别与OA、OB相交于点E、F(如图12-5(1)).度量PE、PF的长度,这两条线段相等吗?
(2)把三角尺绕点P旋转(如图12-5(2)),PE与PF相等吗?
在后续的学习中,可以证实:图12-4(2)不是长方形;图12-5中PE与PF相等.
图12-5
如图的图案是一个轴对称图形(不考虑颜色),直线l 是它的一条对称轴.已知图中圆的半径为r,求绿色部分的面积.
解:如果以直线l为对称轴,把l左边绿色部分反射到l的右边,那么它们的像恰好填补了右边白色部分.所以图中的绿色部分的面积等于半圆的面积是 .
命题,有真命题,也有假命题.要说明一个命题是假命题,只要举出反例即可.
要说明一个命题是真命题,则要从命题的条件出发,根据已学过的基本事实、定义、性质、和定理等,进行有理有据的推理.这种推理的过程叫做证明(proof).经过证明的真命题称为定理(theorem).
想一想:
(1)根据“两条平行线被第三条直线所截,内错角相等”.你能作出相关的图形吗?
(2)你能根据所作的图形写出已知、求证吗?
(3)你能说说证明的思路吗?
1
a
b
c
2
3
已知,如图, 直线a//b, ∠1和∠2是直线a、b被直线c截出的内错角.
求证:∠1=∠2
已知:如图,直线a∥b, ∠1和∠2
是直线a、b被直线 c截出的内错角 .
求证:∠1=∠2
1
2
3
a
b
c
证明:∵a∥b ( )
∴∠3=∠2
( )
∵ ∠3=∠1 ( )
∴∠1=∠2 ( )
已知
两直线平行,同位角相等
对顶角相等
等量代换
做一做:
两条平行线被第三条直线所截,同旁内角互补.
已知:如图,直线a//b,∠1和∠2是直线a,b被直线c截出的同旁内角.
求证:∠1+∠2=180°
证: a//b(已知)
∠3=∠2(两直线平行,同位角相等)
∠1+∠3=180°(1平角=180° )
∠1+∠2=180°(等量代换)
已知:如图,直线a//b,∠1和∠2是直线a,b被直线c截出的同旁内角.
求证:∠1+∠2=180°
证明的一般步骤:
第一步:根据题意,画出图形.
先根据命题的条件即已知事项,画出图形,再把命题的结论即求证的需要在图上标出必要的字母或符号,以便于叙述或推理过程的表达.
第二步:根据条件、结论,结合图形,写出已知、求证.把命题的条件化为几何符号的语言写在已知中,命题的结论转化为几何符号的语言写在求证中.
第三步:经过分析,找出由已知推出求证的途径,写出证明过程.
一般情况下,分析的过程不要求写出来,有些题目中,已经画出了图形,写好了已知、 求证,这时只要写出“证明”一项就可以了.
例1 已知:如图12-7,直线AB、CD被直线EF所截,AB∥CD,MG平分∠EMB,NH平分∠END.
求证:MG∥NH.
证明:∵AB∥CD(已知),
∴∠EMB=∠END(两直线平行,同位角相等).
∵MG平分∠EMB,NH平分∠END(已知),
∴∠EMG= ∠EMB,∠ENH= ∠END(角平分线的定义).
∴∠EMG=∠ENH(等量代换).
∴MG∥NH(同位角相等,两直线平行).
根据下列命题,画出图形,并结合图形
写出已知、求证(不写证明过程):
(1)垂直于同一直线的两直线平行;
已知:直线b⊥a , c⊥a
a
b
c
求证:b∥c
做一做
(2)一个角的平分线上的点到这个角的两
边的距离相等;
A
B
O
C
E
F
G
已知:如图,OC是∠AOB的平分线,
EF⊥OA于F ,
EG⊥OB于G
求证:EF=EG
做一做
(3)如果两条直线都和第三条直线平行,
那么这两条直线也互相平行.
已知:如图,直线a,b,c被直线d所
截,且a∥b ,c∥b,
求证:a∥c
a
b
c
d
做一做
A
B
C
对于三角形,我们已经有哪些认识?
合作探索
定义
分类
内角和
外角和
…………
实验1:先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图1),然后把另处两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果.
A
C
B
图1
B
A
C
图2
B A
C
图3
B A C
图4
求证:三角形三个内角的和等于180?.
1
1
2
A
B
D
2
3
C
1
2
实验2: 将纸片三角形顶角剪下,随意将它们拼凑在一起.
在证明三角形内角和时,小明的想法是把三个角“凑”到A处,他过点A作直线DE//BC,(如图).他的想法可行吗?
A
B
C
E
D
证明 过点A作DE∥BC.则
∠C=∠CAE,∠B=∠BAD(两直线平行,内错角相等)
∴∠BAC+∠B+∠C=∠BAC+∠BAD+∠CAE
=∠DAE=180?(平角的定义)
你还有其他的证明方法么?
辅助线
已知:如图, △ABC.
求证:
∠A+∠B+∠C=180°
A
B
C
1
2
D
E
证明: 作BC的延长线CD,过点C作射线CE//AB,则
∠1=∠A(两直线平行,内错角相等)
∠2=∠B(两直线平行,同位角相等)
∠1+∠2+∠ACB=180°
∠A+∠B+∠ACB=180°
A
B
C
E
图1
E
A
B
C
D
F
图2
A
N
B
C
T
S
图3
P
Q
R
M
A
N
B
C
T
S
图4
P
Q
R
M
关于辅助线:
3、添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题转化,要根据需要而定,平时做题时要注意总结.
2、它的作用是把分散的条件集中,把隐含的条件显现出来,起到牵线搭桥的作用.
1、辅助线是为了证明需要在原图上添画的线.(辅助线通常画成虚线)
三角形内角和定理:三角形的三个内角的和等于180°.
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
推论:
已知:
求证:
证明:
如图,∠ACD是△ABC的一个外角
∠ACD =∠A+∠B
A
B
C
D
1、三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
A
B
C
3、三角形的一个外角大于任何一个和它不相邻的内角
2、三角形的一个外角等于和它不相邻的两个内角的和
A
B
C
1
2
D
E
∴∠1+∠2 = ∠A+∠B
∴ ∠ACD >∠A,
∠ACD >∠B
三角形内角和定理的几何表述:
例2 已知:如图12-9,AC、BD相交于点O.
求证:∠A+ ∠B= ∠C+ ∠D.
证明:在△AOB中, ∠A+ ∠B+ ∠AOB=180 °(三角形三个内角的和等于180 °).
∴ ∠A+ ∠B=180 °-∠AOB(等式性质).
在△COD中,同理可得
∠C+ ∠D=180 °-∠COD.
∵∠AOB= ∠COD(对顶角相等).
∴ ∠A+ ∠B=∠C+ ∠D(等量代换).
已知命题:如图,点A,D,B,E在同一直线上,且AD=BE,AC∥DF,则△ABC≌△DEF.这个命题是真命题还是假命题?
A
D
B
E
C
F
如果是真命题,请给出证明;
如果是假命题,请添加适当的条件,使它成为真命题.你有几种不同的添加方法?
1.图中两条线段AB与BC的长度相等吗?请你先观察,再度量.
观察AB与BC,容易得到AB比BC长.
经过度量,得到AB=BC,可见直接观察是不准确的.
2.图中两组圆的中央各有一个圆,这两个圆一样大吗?请你先观察,在度量.
观察两个圆,容易得到周围是小圆的圆较大.
经过度量,两个圆的大小是相等的,观察是不准确的.
3.(1)任意写2个相邻偶数,计算较大偶数的平方 减去较小偶数的平方差;
(2)换2个相邻偶数,仿照(1)再试试,你发现了什么?
(3)证实你发现的结论.
(1)例如:取4,2;则42-22=12.
(2)例如:取8,6;则82-62=28.
发现(2(n+1))2-(2n)2=4(2n+1)(n为正整数).
(3)证明:
取n为正整数,则一偶数为2n,相邻的偶数可取2(n+1);
(2(n+1))2-(2n)2
=4(n2+2n+1)-4n2
=4(2n+1).
填写下列推理中的空格(第1、2题):
1.如图,点A、B、E在一条直线上.
(1)∵∠1=∠3(已知)
∴AB∥DC( );
(2)∵∠DAE=∠CBE(已知),
∴AD∥BC( );
(3)∵∠CDA+∠DAB=180?(已知),
∴AB∥DC( );
(4)∠2=∠4(已知),
∴___________∥___________(内错角相等,两直线平行);
内错角相等,两直线平行
同位角相等,两直线平行
同旁内角互补,两直线平行
AD
BC
(5)∵∠DCB+∠ABC=180?(已知),
∴___________∥____________(同旁内角互补,两直线平行);
(6)∵∠DAB+∠ABC=180?(已知),
∴___________∥____________(同旁内角互补,两直线平行).
AB
DC
AD
BC
2.已知:如图,∠BAD=∠DCB,∠1=∠3.
求证:AD∥BC.
证明:∵∠BAD=∠DCB,∠1=∠3( ),
∴∠BAD-∠_________=∠DCB-∠_________(等式性质),
即 ∠___________=∠___________.
∴AD∥BC( ).
已知
1
3
2
4
内错角相等,两直线平行
3.已知:如图,a∥b,c∥d,∠1=50?.
求证:∠2=130?.
3
4
证明:
在图上另取两个角∠3,∠4,如图所示:
∵ c∥d ,
∴∠1=∠3(两直线平行,同位角相等);
又∵ a∥b,
∴∠3=∠4(两直线平行,同位角相等);
∴∠1= ∠4,
∴∠2=180?- ∠4=180?-∠1=130?
已知:如图,AD是△ABC的角平分线,E是BC延长线上一点,∠EAC=∠B.
求证:∠ADE=∠DAE.
证明:
∵AD是△ABC的角平分线,
∴∠BAD=∠DAC;
∵∠BAD+∠B= ∠ADE(三角形的一个外角等于它不相邻的两个内角和),
∠EAC+ ∠DAC= ∠DAE;
又∵ ∠EAC=∠B,
∴ ∠ADE=∠DAE.
经过刚才的“证明”之旅,你能说出完整的几何命题证明需要哪几个步骤吗?
小结
(1)根据题意,画出图形.
(2)在“已知”中写出条件, 在“求证”中写出结论.
(3)在“证明”中写出推理过程,并且步步有据.
谢谢聆听
12.2 证明
第12章 证明
2020-2021学年度苏科版七年级下册
欣赏判断
观察图片,蓝色的粗线是直的吗?
观察图形,一组直线a,b,c,d是否都互相平行?
在图12-1中,两条线段AB与CD哪一条长一些?
图12-1
看上去线段AB比线段CD长.
通过度量线段AB、CD的长度,可以证实:线段CD比线段AB长.
试一试
把图12-2(1)长方形草坪中间lm宽的直道,改成图12-2(2)中处处1m宽的“曲径”.
这两条小道的面积相等吗?
议一议
图12-2
如果将图12-2(2)中小道左边的草坪
向右平移1m,那么得到一个长为(a-1)m、宽为bm的长方形(如图12-3),它的面积为b(a-1)m2.
于是,“曲径”的面积为ab-b(a-1)=
ab-ab+b=b(m2).
由图12-2(1)可知直道的面积为
1×b=b(m2).
通过图形的平移和计算,可以证实:两条小道的面积等.
图12-3
如图,在长方形ABCD中,横向阴影部分是长方形,另一阴影部分是平形四边形,根据图中标明的数据,计算空白部分的面积?
c
c
a
b
A
C
D
B
c
c
a
b
A
C
D
B
图 1
图 2
点拔:这里通过平移,避免了对图形分别计算面积,
使求解简洁方便.
析解:利用“平移不改变图形的形状与大小”这一性质可以迅速解决本题.由图可知,四个空白四边形经过平移可以组成一个长方形,它的长为(a-c),宽为(b-c),所以空白部分的面积为:(a-c)(b-c)=ab-ac-bc+c2
1.图12-4(l)是一张8×8的正方形纸片,把它剪成4块,按图12-4(2)重新拼合.
这4块纸片恰好能拼成一个长为13、宽为5的长方形吗?
图12-4
2.画∠AOB=90°,并画∠AOB的平分线OC.
(1)把三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边分别与OA、OB相交于点E、F(如图12-5(1)).度量PE、PF的长度,这两条线段相等吗?
(2)把三角尺绕点P旋转(如图12-5(2)),PE与PF相等吗?
在后续的学习中,可以证实:图12-4(2)不是长方形;图12-5中PE与PF相等.
图12-5
如图的图案是一个轴对称图形(不考虑颜色),直线l 是它的一条对称轴.已知图中圆的半径为r,求绿色部分的面积.
解:如果以直线l为对称轴,把l左边绿色部分反射到l的右边,那么它们的像恰好填补了右边白色部分.所以图中的绿色部分的面积等于半圆的面积是 .
命题,有真命题,也有假命题.要说明一个命题是假命题,只要举出反例即可.
要说明一个命题是真命题,则要从命题的条件出发,根据已学过的基本事实、定义、性质、和定理等,进行有理有据的推理.这种推理的过程叫做证明(proof).经过证明的真命题称为定理(theorem).
想一想:
(1)根据“两条平行线被第三条直线所截,内错角相等”.你能作出相关的图形吗?
(2)你能根据所作的图形写出已知、求证吗?
(3)你能说说证明的思路吗?
1
a
b
c
2
3
已知,如图, 直线a//b, ∠1和∠2是直线a、b被直线c截出的内错角.
求证:∠1=∠2
已知:如图,直线a∥b, ∠1和∠2
是直线a、b被直线 c截出的内错角 .
求证:∠1=∠2
1
2
3
a
b
c
证明:∵a∥b ( )
∴∠3=∠2
( )
∵ ∠3=∠1 ( )
∴∠1=∠2 ( )
已知
两直线平行,同位角相等
对顶角相等
等量代换
做一做:
两条平行线被第三条直线所截,同旁内角互补.
已知:如图,直线a//b,∠1和∠2是直线a,b被直线c截出的同旁内角.
求证:∠1+∠2=180°
证: a//b(已知)
∠3=∠2(两直线平行,同位角相等)
∠1+∠3=180°(1平角=180° )
∠1+∠2=180°(等量代换)
已知:如图,直线a//b,∠1和∠2是直线a,b被直线c截出的同旁内角.
求证:∠1+∠2=180°
证明的一般步骤:
第一步:根据题意,画出图形.
先根据命题的条件即已知事项,画出图形,再把命题的结论即求证的需要在图上标出必要的字母或符号,以便于叙述或推理过程的表达.
第二步:根据条件、结论,结合图形,写出已知、求证.把命题的条件化为几何符号的语言写在已知中,命题的结论转化为几何符号的语言写在求证中.
第三步:经过分析,找出由已知推出求证的途径,写出证明过程.
一般情况下,分析的过程不要求写出来,有些题目中,已经画出了图形,写好了已知、 求证,这时只要写出“证明”一项就可以了.
例1 已知:如图12-7,直线AB、CD被直线EF所截,AB∥CD,MG平分∠EMB,NH平分∠END.
求证:MG∥NH.
证明:∵AB∥CD(已知),
∴∠EMB=∠END(两直线平行,同位角相等).
∵MG平分∠EMB,NH平分∠END(已知),
∴∠EMG= ∠EMB,∠ENH= ∠END(角平分线的定义).
∴∠EMG=∠ENH(等量代换).
∴MG∥NH(同位角相等,两直线平行).
根据下列命题,画出图形,并结合图形
写出已知、求证(不写证明过程):
(1)垂直于同一直线的两直线平行;
已知:直线b⊥a , c⊥a
a
b
c
求证:b∥c
做一做
(2)一个角的平分线上的点到这个角的两
边的距离相等;
A
B
O
C
E
F
G
已知:如图,OC是∠AOB的平分线,
EF⊥OA于F ,
EG⊥OB于G
求证:EF=EG
做一做
(3)如果两条直线都和第三条直线平行,
那么这两条直线也互相平行.
已知:如图,直线a,b,c被直线d所
截,且a∥b ,c∥b,
求证:a∥c
a
b
c
d
做一做
A
B
C
对于三角形,我们已经有哪些认识?
合作探索
定义
分类
内角和
外角和
…………
实验1:先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图1),然后把另处两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果.
A
C
B
图1
B
A
C
图2
B A
C
图3
B A C
图4
求证:三角形三个内角的和等于180?.
1
1
2
A
B
D
2
3
C
1
2
实验2: 将纸片三角形顶角剪下,随意将它们拼凑在一起.
在证明三角形内角和时,小明的想法是把三个角“凑”到A处,他过点A作直线DE//BC,(如图).他的想法可行吗?
A
B
C
E
D
证明 过点A作DE∥BC.则
∠C=∠CAE,∠B=∠BAD(两直线平行,内错角相等)
∴∠BAC+∠B+∠C=∠BAC+∠BAD+∠CAE
=∠DAE=180?(平角的定义)
你还有其他的证明方法么?
辅助线
已知:如图, △ABC.
求证:
∠A+∠B+∠C=180°
A
B
C
1
2
D
E
证明: 作BC的延长线CD,过点C作射线CE//AB,则
∠1=∠A(两直线平行,内错角相等)
∠2=∠B(两直线平行,同位角相等)
∠1+∠2+∠ACB=180°
∠A+∠B+∠ACB=180°
A
B
C
E
图1
E
A
B
C
D
F
图2
A
N
B
C
T
S
图3
P
Q
R
M
A
N
B
C
T
S
图4
P
Q
R
M
关于辅助线:
3、添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题转化,要根据需要而定,平时做题时要注意总结.
2、它的作用是把分散的条件集中,把隐含的条件显现出来,起到牵线搭桥的作用.
1、辅助线是为了证明需要在原图上添画的线.(辅助线通常画成虚线)
三角形内角和定理:三角形的三个内角的和等于180°.
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
推论:
已知:
求证:
证明:
如图,∠ACD是△ABC的一个外角
∠ACD =∠A+∠B
A
B
C
D
1、三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
A
B
C
3、三角形的一个外角大于任何一个和它不相邻的内角
2、三角形的一个外角等于和它不相邻的两个内角的和
A
B
C
1
2
D
E
∴∠1+∠2 = ∠A+∠B
∴ ∠ACD >∠A,
∠ACD >∠B
三角形内角和定理的几何表述:
例2 已知:如图12-9,AC、BD相交于点O.
求证:∠A+ ∠B= ∠C+ ∠D.
证明:在△AOB中, ∠A+ ∠B+ ∠AOB=180 °(三角形三个内角的和等于180 °).
∴ ∠A+ ∠B=180 °-∠AOB(等式性质).
在△COD中,同理可得
∠C+ ∠D=180 °-∠COD.
∵∠AOB= ∠COD(对顶角相等).
∴ ∠A+ ∠B=∠C+ ∠D(等量代换).
已知命题:如图,点A,D,B,E在同一直线上,且AD=BE,AC∥DF,则△ABC≌△DEF.这个命题是真命题还是假命题?
A
D
B
E
C
F
如果是真命题,请给出证明;
如果是假命题,请添加适当的条件,使它成为真命题.你有几种不同的添加方法?
1.图中两条线段AB与BC的长度相等吗?请你先观察,再度量.
观察AB与BC,容易得到AB比BC长.
经过度量,得到AB=BC,可见直接观察是不准确的.
2.图中两组圆的中央各有一个圆,这两个圆一样大吗?请你先观察,在度量.
观察两个圆,容易得到周围是小圆的圆较大.
经过度量,两个圆的大小是相等的,观察是不准确的.
3.(1)任意写2个相邻偶数,计算较大偶数的平方 减去较小偶数的平方差;
(2)换2个相邻偶数,仿照(1)再试试,你发现了什么?
(3)证实你发现的结论.
(1)例如:取4,2;则42-22=12.
(2)例如:取8,6;则82-62=28.
发现(2(n+1))2-(2n)2=4(2n+1)(n为正整数).
(3)证明:
取n为正整数,则一偶数为2n,相邻的偶数可取2(n+1);
(2(n+1))2-(2n)2
=4(n2+2n+1)-4n2
=4(2n+1).
填写下列推理中的空格(第1、2题):
1.如图,点A、B、E在一条直线上.
(1)∵∠1=∠3(已知)
∴AB∥DC( );
(2)∵∠DAE=∠CBE(已知),
∴AD∥BC( );
(3)∵∠CDA+∠DAB=180?(已知),
∴AB∥DC( );
(4)∠2=∠4(已知),
∴___________∥___________(内错角相等,两直线平行);
内错角相等,两直线平行
同位角相等,两直线平行
同旁内角互补,两直线平行
AD
BC
(5)∵∠DCB+∠ABC=180?(已知),
∴___________∥____________(同旁内角互补,两直线平行);
(6)∵∠DAB+∠ABC=180?(已知),
∴___________∥____________(同旁内角互补,两直线平行).
AB
DC
AD
BC
2.已知:如图,∠BAD=∠DCB,∠1=∠3.
求证:AD∥BC.
证明:∵∠BAD=∠DCB,∠1=∠3( ),
∴∠BAD-∠_________=∠DCB-∠_________(等式性质),
即 ∠___________=∠___________.
∴AD∥BC( ).
已知
1
3
2
4
内错角相等,两直线平行
3.已知:如图,a∥b,c∥d,∠1=50?.
求证:∠2=130?.
3
4
证明:
在图上另取两个角∠3,∠4,如图所示:
∵ c∥d ,
∴∠1=∠3(两直线平行,同位角相等);
又∵ a∥b,
∴∠3=∠4(两直线平行,同位角相等);
∴∠1= ∠4,
∴∠2=180?- ∠4=180?-∠1=130?
已知:如图,AD是△ABC的角平分线,E是BC延长线上一点,∠EAC=∠B.
求证:∠ADE=∠DAE.
证明:
∵AD是△ABC的角平分线,
∴∠BAD=∠DAC;
∵∠BAD+∠B= ∠ADE(三角形的一个外角等于它不相邻的两个内角和),
∠EAC+ ∠DAC= ∠DAE;
又∵ ∠EAC=∠B,
∴ ∠ADE=∠DAE.
经过刚才的“证明”之旅,你能说出完整的几何命题证明需要哪几个步骤吗?
小结
(1)根据题意,画出图形.
(2)在“已知”中写出条件, 在“求证”中写出结论.
(3)在“证明”中写出推理过程,并且步步有据.
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
