7.3 频数和频率(第2课时) 课件(共34张PPT)
文档属性
| 名称 | 7.3 频数和频率(第2课时) 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 18:57:13 | ||
图片预览










文档简介
7.3
频数与频率
第2课时
第7章
数据的收集、整理、描述
2020-2021学年度苏科版八年级下册
1.中位数和众数的定义:
我们把一组数据中出现次数最多的那个数据
叫做这组数据的众数.
如果把这组数据按大小顺序排列,位于最中间的
一个数据叫做这组数据的中位数.
(如果总共有偶数个数据时,则最中间两个数
据的平均数作为这组数据的中位数).
课前热身
2.
方差的概念
设在一组数据
中,各数据与它们的平
均数
的差的平方分别是
,
那么
,我们用它们的平均数,即用
来衡量这组数据的波动大小,并把它叫做这组
数据的方差.
一组数据方差越大,说明这组数据波动越大.
数学实验室:为了增强环境保护意识,学校举办“环保节”,要求每班选出1名“环保小卫士”,选举办法如下:
(1)民主提名候选人,全班同学举手表决,得票数较多得前3名为正式候选人;
(2)再同一发放得白纸(选票)上,各自写上你认为应当选的1名候选人名字;
(3)将选票投入票箱;
(4)由全班推选的3位同学分别唱票、监票和记录统计;
(5)根据统计结果,得票最多得同学当选为“环保小卫士”.
下表为四川卧龙大熊猫保护研究中心的30只成年大熊猫的体重(单位:kg):
问题:这30只成年大熊猫体重在哪一个范围内只数最多,在哪一个范围内只数最少?
一组数据的最大值与最小值的差叫做极差.
110
104
120
115
99
135
86
132
109
93
116
98
126
117
96
107
116
87
109
113
142
108
123
113
94
104
109
139
101
102
86
142
组
别(kg)
划
记
只
数
85.5~95.5
95.5~105.5
正
105.5~115.5
正
115.5~125.5
正
125.5~135.5
135.5~145.5
合计
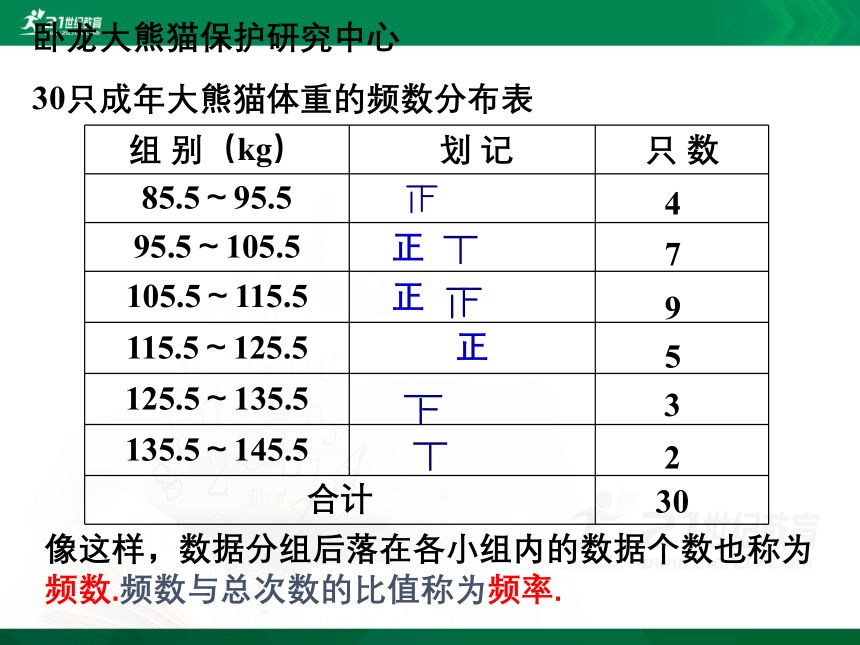
卧龙大熊猫保护研究中心
30只成年大熊猫体重的频数分布表
4
7
9
5
3
30
2
像这样,数据分组后落在各小组内的数据个数也称为频数.频数与总次数的比值称为频率.
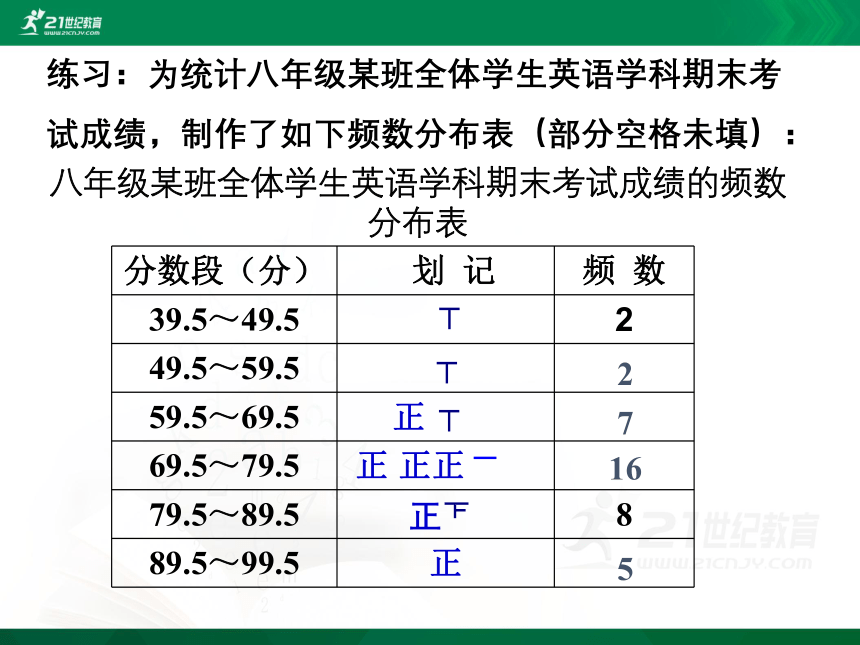
练习:为统计八年级某班全体学生英语学科期末考试成绩,制作了如下频数分布表(部分空格未填):
八年级某班全体学生英语学科期末考试成绩的频数分布表
分数段(分)
划
记
频
数
39.5~49.5
2
49.5~59.5
59.5~69.5
正
69.5~79.5
正
正正
79.5~89.5
8
89.5~99.5
正
2
7
16
5
正
(1)请完成上面的频数分布表;
(2)数据分组时的组距为多少?估计极差至多为多少?
(3)该班有多少学生?
(4)哪一个分数段的学生人数最多?哪一个分数段的学生人数最少?80分以上(包括
80分)有多少人?占全班人数的百分之几?
组距为10分,
极差至多为60分
40名
69.5~79.5的学生人数最多,
39.5~49.5与49.5~59.5这两个分数段人数最少,
80分以上有13人,占全班人数的32.5%.
课外练习:
1.一个自由转动的转盘如图.让自由转动20次,记录每次指针所在区域的颜色如下:
黄,
红,
红,
绿,
绿,
绿,
黄,
黄,
红,
黄,
绿,
黄,
红,
红,
绿,
红,
绿,
红,
绿,
绿.
请制作反映指针所在区域颜色的频数分布表.
2.抽查20名新生婴儿的血型
A,B,A,B,B,O,AB,A,A,O
A,B,A,A,B,AB,O,A,B,A
20名新生婴儿血型的频数表
组别
划记
频数
A型
B型
AB型
O型
9
6
2
3
类别
次数
按
分组,频数
为了增强环境保护意识,昭阳湖初级中学举办“环保节”,要求每班选出1名“环保小卫士”,选举办法如下:(有3名候选人:王小明
杨丽
方舟)
(1)
每人在选票上写上1名自己认为最合适的候选人姓名,将选票投入投票箱;
(2)由全班推选代表分别唱票、监票和记录统计;
(3)根据统计结果,得票最多的同学当选为“环保小卫士”.
问题情境:
下表是某班选“环保卫士”时的统计表格
候选人
唱票记录
得票数
得票率
王小明
杨
丽
方
舟
10
18
12
0.25
0.45
0.3
正
正
正正T
正正正
频数:
某个对象出现的次数称为频数
频率:
频数与总次数的比值称为频率
例1.下表为某班小步训练的数学成绩统计如下:
分数段
100
90—99
80--89
70--79
60--69
0--59
人数
2
6
12
21
7
2
规定:80分以上(包括80分)定为成绩优秀,
60分以上(包括60分)定为成绩及格。
在这个班级的这次成绩统计中,
成绩为优秀的频数是
,频率是
;
例2:某班20名女生的身高如下(单位:cm):
153,156,152,158,156,160,163,145,
152,153,162,153,165,150,157,153,
158,157,158,158.
请在表中填出身高在以下各范围内的频数与频率
?
身高
140—149.5
149.5—159.5
159.5—170
频数
频率
划记
某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、
C、D四类.
其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别
A
B
C
D
频数
30
40
24
b
频率
a
0.4
0.24
0.06
类别
A
B
C
D
频数
30
40
24
b
频率
a
0.4
0.24
0.06
(1)表中的a= ,b= ;
(2)根据表中数据,求扇形
统计图中类别为B的学生数所
对应的扇形圆心角的度数;
(3)若该校有学生1000名,
根据调查结果估计该校学生
中类别为C的人数约为多少?
课堂练习:
1.频率不可能取到的数为(
)
A.
0
B.
0.5
C.
1
D.
1.5
2.某校七年级共有1000人,为了了解这些学生的视力情况,随机抽查了20名学生的视力,对所得数据进行整理。若数据在0.95~1.15这一小组的频率为0.3,则可估计该校七年级学生视力在0.95~1.15范围内的人数有(
)
A.600
B.300
C.150
D.30
3.期末统考中,A校优秀人数占20%,B校优秀人数占25%,则两校优生人数(
)
A.
A校多于B校
B.B校多于A校
C.
A、B校—样多
D.无法比较
4.小刚将一个骰子随意抛了10次。出现的点数分别为6、3、1、2、3、4、3、5、3、4。在这10次中“4”出现的频数是
,3出现频率是
.
5.某班有50名学生,现在按他们的出生年月不同将他们分成4组,其中4~6月份组的频率为0.32,那么这个小组有_______位同学.
6.某企业生产纯平彩电10000台,其中9000台为优等品,另外600台为一等品,200台为二等品,100台为三等品,还有100台为次品,试计算该企业生产的纯平彩电合格品(非次品)的频率与频数。
优等品的频率是多少?合格品的频率是多少?次品的频率是多少?
7.某校七年级部分学生引体向上的成绩分成五组,第一、二、三、四组的频率分别为0.05,0.15,0.25,0.30;第五组的频数是25.回答下列问题:
(1)第五组的频率是多少?
(2)参加本次测试的学生总数是多少?
1.填写下列频数表中未完成的部分.
{F5AB1C69-6EDB-4FF4-983F-18BD219EF322}组别
频数
频率
A
11
0.11
B
13
C
D
0.10
合计
1.00
0.13
0.66
100
10
66
2.车站增加自动售票机售票后大大缩短了购票者排队等候的时间.一名记者在车站随机访问了25位购票者,了解到他们排队等候的时间分别为(单位:分):
1,2,2,2,1,3,4,2,2,2,2,3,1,3,4,5,3,2,12,2,3,2,3,2
(1)请填写如下的频数表:
{F5AB1C69-6EDB-4FF4-983F-18BD219EF322}组别(分)
划记
频数
频率
1
2
3
4
5
4
12
6
2
1
0.16
0.04
0.08
0.24
0.48
(2)求出等待时间为2分钟和3分钟的人数和所占的百分比.
等待2分钟的人数:
等待3分钟的人数:
12
48%
所占百分比:
6
所占百分比:
24%
2.车站增加自动售票机售票后大大缩短了购票者排队等候的时间.一名记者在车站随机访问了25位购票者,了解到他们排队等候的时间分别为(单位:分):
1,2,2,2,1,3,4,2,2,2,2,3,1,3,4,5,3,2,12,2,3,2,3,2
1.某校为了了解七年级350名学生的数学学习情况,从该年级任意抽取了50名学生进行测试,结果如下(单位:分)
93,92,75,77,72,73,84,67,95,84,
86,71,96,84,85,89,92,74,73,83,
40,68,81,98,94,89,92,99,70,82,
72,93,68,85,86,75,83,78,92,60,
89,52,96,83,92,86,67,77,57,77.
分组
频数统计
频数
39.5~49.5
49.5~59.5
59.5~69.5
69.5~79.5
79.5~89.5
89.5~99.5
合计
(1)请你完成下面的频数分布表:
1
2
5
13
16
13
50
(2)画出频数直方图;
频数
分组
0
2
4
6
8
10
12
14
16
18
20
39.5
49.5
59.5
69.5
79.5
89.5
99.5
(3)试估计该校七年级有多少名学生数学成绩在80分(含80分)以上.
经计算,这50名学生测试结果达到80分以上的占58%,用这50名学生测试达到80分以上的比率估计七年级350名学生成绩达到80以上的人数,即350×58%=203(人).
2.某林业局对林区内树木的生长情况进行抽样调查,测得一些树干的树围长度(单位:m),并列出如下的频数分布表:
分组
0.4~0.5
0.5~0.6
0.6~0.7
0.7~0.8
0.8~0.9
0.9~1.0
1.0~1.1
1.1~1.2
频数
3
9
18
30
20
10
7
3
(1)画出频数直方图;
频数
分组
0
3
6
9
12
15
18
21
24
27
30
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
(2)求树围长度为0.6~1.0m之间的树木数占总树木数的百分率.
抽出的树木中树围长度为0.6~1.0m之间的树木数为78棵抽出的数目总数为100棵,因此估计树木中树围长度为0.6~1.0m之间的树木占总树木数的百分率为78%.
本课总结:
通过这节课的学习,你有哪些收获?
什么是频数和频率?
如何计算频率呢?
频率=
频数
总次数
频数=
总次数=
频率
频数
总次数
×
频率
谢谢聆听
频数与频率
第2课时
第7章
数据的收集、整理、描述
2020-2021学年度苏科版八年级下册
1.中位数和众数的定义:
我们把一组数据中出现次数最多的那个数据
叫做这组数据的众数.
如果把这组数据按大小顺序排列,位于最中间的
一个数据叫做这组数据的中位数.
(如果总共有偶数个数据时,则最中间两个数
据的平均数作为这组数据的中位数).
课前热身
2.
方差的概念
设在一组数据
中,各数据与它们的平
均数
的差的平方分别是
,
那么
,我们用它们的平均数,即用
来衡量这组数据的波动大小,并把它叫做这组
数据的方差.
一组数据方差越大,说明这组数据波动越大.
数学实验室:为了增强环境保护意识,学校举办“环保节”,要求每班选出1名“环保小卫士”,选举办法如下:
(1)民主提名候选人,全班同学举手表决,得票数较多得前3名为正式候选人;
(2)再同一发放得白纸(选票)上,各自写上你认为应当选的1名候选人名字;
(3)将选票投入票箱;
(4)由全班推选的3位同学分别唱票、监票和记录统计;
(5)根据统计结果,得票最多得同学当选为“环保小卫士”.
下表为四川卧龙大熊猫保护研究中心的30只成年大熊猫的体重(单位:kg):
问题:这30只成年大熊猫体重在哪一个范围内只数最多,在哪一个范围内只数最少?
一组数据的最大值与最小值的差叫做极差.
110
104
120
115
99
135
86
132
109
93
116
98
126
117
96
107
116
87
109
113
142
108
123
113
94
104
109
139
101
102
86
142
组
别(kg)
划
记
只
数
85.5~95.5
95.5~105.5
正
105.5~115.5
正
115.5~125.5
正
125.5~135.5
135.5~145.5
合计
卧龙大熊猫保护研究中心
30只成年大熊猫体重的频数分布表
4
7
9
5
3
30
2
像这样,数据分组后落在各小组内的数据个数也称为频数.频数与总次数的比值称为频率.
练习:为统计八年级某班全体学生英语学科期末考试成绩,制作了如下频数分布表(部分空格未填):
八年级某班全体学生英语学科期末考试成绩的频数分布表
分数段(分)
划
记
频
数
39.5~49.5
2
49.5~59.5
59.5~69.5
正
69.5~79.5
正
正正
79.5~89.5
8
89.5~99.5
正
2
7
16
5
正
(1)请完成上面的频数分布表;
(2)数据分组时的组距为多少?估计极差至多为多少?
(3)该班有多少学生?
(4)哪一个分数段的学生人数最多?哪一个分数段的学生人数最少?80分以上(包括
80分)有多少人?占全班人数的百分之几?
组距为10分,
极差至多为60分
40名
69.5~79.5的学生人数最多,
39.5~49.5与49.5~59.5这两个分数段人数最少,
80分以上有13人,占全班人数的32.5%.
课外练习:
1.一个自由转动的转盘如图.让自由转动20次,记录每次指针所在区域的颜色如下:
黄,
红,
红,
绿,
绿,
绿,
黄,
黄,
红,
黄,
绿,
黄,
红,
红,
绿,
红,
绿,
红,
绿,
绿.
请制作反映指针所在区域颜色的频数分布表.
2.抽查20名新生婴儿的血型
A,B,A,B,B,O,AB,A,A,O
A,B,A,A,B,AB,O,A,B,A
20名新生婴儿血型的频数表
组别
划记
频数
A型
B型
AB型
O型
9
6
2
3
类别
次数
按
分组,频数
为了增强环境保护意识,昭阳湖初级中学举办“环保节”,要求每班选出1名“环保小卫士”,选举办法如下:(有3名候选人:王小明
杨丽
方舟)
(1)
每人在选票上写上1名自己认为最合适的候选人姓名,将选票投入投票箱;
(2)由全班推选代表分别唱票、监票和记录统计;
(3)根据统计结果,得票最多的同学当选为“环保小卫士”.
问题情境:
下表是某班选“环保卫士”时的统计表格
候选人
唱票记录
得票数
得票率
王小明
杨
丽
方
舟
10
18
12
0.25
0.45
0.3
正
正
正正T
正正正
频数:
某个对象出现的次数称为频数
频率:
频数与总次数的比值称为频率
例1.下表为某班小步训练的数学成绩统计如下:
分数段
100
90—99
80--89
70--79
60--69
0--59
人数
2
6
12
21
7
2
规定:80分以上(包括80分)定为成绩优秀,
60分以上(包括60分)定为成绩及格。
在这个班级的这次成绩统计中,
成绩为优秀的频数是
,频率是
;
例2:某班20名女生的身高如下(单位:cm):
153,156,152,158,156,160,163,145,
152,153,162,153,165,150,157,153,
158,157,158,158.
请在表中填出身高在以下各范围内的频数与频率
?
身高
140—149.5
149.5—159.5
159.5—170
频数
频率
划记
某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、
C、D四类.
其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别
A
B
C
D
频数
30
40
24
b
频率
a
0.4
0.24
0.06
类别
A
B
C
D
频数
30
40
24
b
频率
a
0.4
0.24
0.06
(1)表中的a= ,b= ;
(2)根据表中数据,求扇形
统计图中类别为B的学生数所
对应的扇形圆心角的度数;
(3)若该校有学生1000名,
根据调查结果估计该校学生
中类别为C的人数约为多少?
课堂练习:
1.频率不可能取到的数为(
)
A.
0
B.
0.5
C.
1
D.
1.5
2.某校七年级共有1000人,为了了解这些学生的视力情况,随机抽查了20名学生的视力,对所得数据进行整理。若数据在0.95~1.15这一小组的频率为0.3,则可估计该校七年级学生视力在0.95~1.15范围内的人数有(
)
A.600
B.300
C.150
D.30
3.期末统考中,A校优秀人数占20%,B校优秀人数占25%,则两校优生人数(
)
A.
A校多于B校
B.B校多于A校
C.
A、B校—样多
D.无法比较
4.小刚将一个骰子随意抛了10次。出现的点数分别为6、3、1、2、3、4、3、5、3、4。在这10次中“4”出现的频数是
,3出现频率是
.
5.某班有50名学生,现在按他们的出生年月不同将他们分成4组,其中4~6月份组的频率为0.32,那么这个小组有_______位同学.
6.某企业生产纯平彩电10000台,其中9000台为优等品,另外600台为一等品,200台为二等品,100台为三等品,还有100台为次品,试计算该企业生产的纯平彩电合格品(非次品)的频率与频数。
优等品的频率是多少?合格品的频率是多少?次品的频率是多少?
7.某校七年级部分学生引体向上的成绩分成五组,第一、二、三、四组的频率分别为0.05,0.15,0.25,0.30;第五组的频数是25.回答下列问题:
(1)第五组的频率是多少?
(2)参加本次测试的学生总数是多少?
1.填写下列频数表中未完成的部分.
{F5AB1C69-6EDB-4FF4-983F-18BD219EF322}组别
频数
频率
A
11
0.11
B
13
C
D
0.10
合计
1.00
0.13
0.66
100
10
66
2.车站增加自动售票机售票后大大缩短了购票者排队等候的时间.一名记者在车站随机访问了25位购票者,了解到他们排队等候的时间分别为(单位:分):
1,2,2,2,1,3,4,2,2,2,2,3,1,3,4,5,3,2,12,2,3,2,3,2
(1)请填写如下的频数表:
{F5AB1C69-6EDB-4FF4-983F-18BD219EF322}组别(分)
划记
频数
频率
1
2
3
4
5
4
12
6
2
1
0.16
0.04
0.08
0.24
0.48
(2)求出等待时间为2分钟和3分钟的人数和所占的百分比.
等待2分钟的人数:
等待3分钟的人数:
12
48%
所占百分比:
6
所占百分比:
24%
2.车站增加自动售票机售票后大大缩短了购票者排队等候的时间.一名记者在车站随机访问了25位购票者,了解到他们排队等候的时间分别为(单位:分):
1,2,2,2,1,3,4,2,2,2,2,3,1,3,4,5,3,2,12,2,3,2,3,2
1.某校为了了解七年级350名学生的数学学习情况,从该年级任意抽取了50名学生进行测试,结果如下(单位:分)
93,92,75,77,72,73,84,67,95,84,
86,71,96,84,85,89,92,74,73,83,
40,68,81,98,94,89,92,99,70,82,
72,93,68,85,86,75,83,78,92,60,
89,52,96,83,92,86,67,77,57,77.
分组
频数统计
频数
39.5~49.5
49.5~59.5
59.5~69.5
69.5~79.5
79.5~89.5
89.5~99.5
合计
(1)请你完成下面的频数分布表:
1
2
5
13
16
13
50
(2)画出频数直方图;
频数
分组
0
2
4
6
8
10
12
14
16
18
20
39.5
49.5
59.5
69.5
79.5
89.5
99.5
(3)试估计该校七年级有多少名学生数学成绩在80分(含80分)以上.
经计算,这50名学生测试结果达到80分以上的占58%,用这50名学生测试达到80分以上的比率估计七年级350名学生成绩达到80以上的人数,即350×58%=203(人).
2.某林业局对林区内树木的生长情况进行抽样调查,测得一些树干的树围长度(单位:m),并列出如下的频数分布表:
分组
0.4~0.5
0.5~0.6
0.6~0.7
0.7~0.8
0.8~0.9
0.9~1.0
1.0~1.1
1.1~1.2
频数
3
9
18
30
20
10
7
3
(1)画出频数直方图;
频数
分组
0
3
6
9
12
15
18
21
24
27
30
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
(2)求树围长度为0.6~1.0m之间的树木数占总树木数的百分率.
抽出的树木中树围长度为0.6~1.0m之间的树木数为78棵抽出的数目总数为100棵,因此估计树木中树围长度为0.6~1.0m之间的树木占总树木数的百分率为78%.
本课总结:
通过这节课的学习,你有哪些收获?
什么是频数和频率?
如何计算频率呢?
频率=
频数
总次数
频数=
总次数=
频率
频数
总次数
×
频率
谢谢聆听
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
