8.3 频率与概率(第1课时) 课件(共23张PPT)
文档属性
| 名称 | 8.3 频率与概率(第1课时) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 19:38:56 | ||
图片预览






文档简介
第1课时
8.3 频率与概率
第8章 认识概率
2020-2021学年度苏科版八年级下册
(1)海枯石烂
(2)守株待兔
随机事件
不可能事件
(3)水中捞月
不可能事件
(4)种瓜得瓜,种豆得豆.
必然事件
2:在下列词语中,那些是刻画必然事件的,那些是刻画不可能事件的,那些是刻画随机事件的?
1.随机事件、必然事件、不可能事件的定义分别是什么?
知识回顾:
频率:在n次重复试验, 事件A发生了m次(0≦m ≦n) m叫做事件A的频数, 事件A的频数在实验的总次数中的比例 ,叫做事件A出现的频率.
(2)频率的范围:
(3)频率是随机的,在试验前不确定的,就算做同样次数的试验频率都可能不同.
n
m
3、频率的定义是什么?
n
m
A
f
n
=
)
(
理解:
(1)记作:
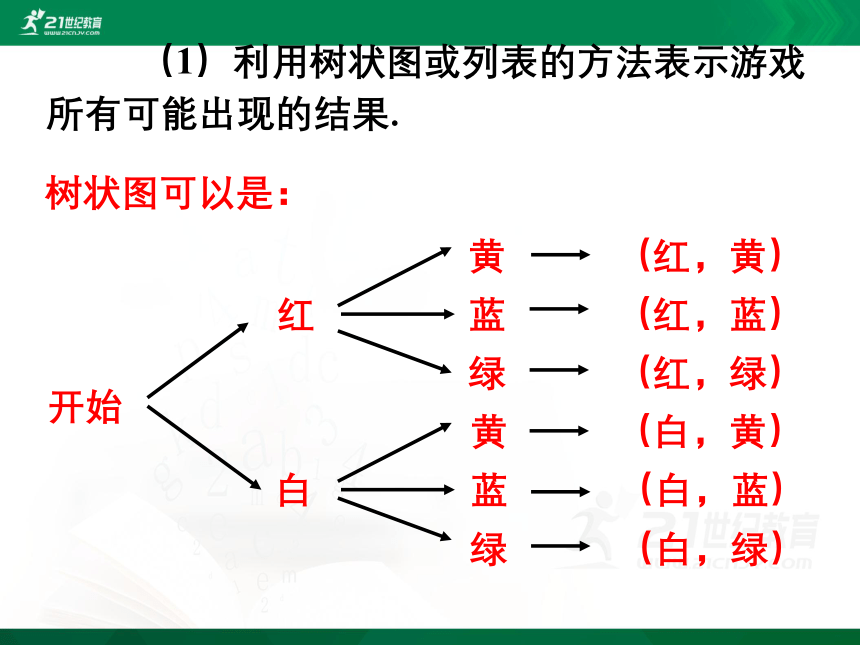
小颖为学校联欢会设计了一个“配紫色”的游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起就配成了紫色.
(1)利用树状图或列表的方法表示游戏所有可能出现的结果.
树状图可以是:
开始
红
白
黄
蓝
绿
(红,黄)
(红,蓝)
(红,绿)
(白,黄)
(白,蓝)
(白,绿)
黄
蓝
绿
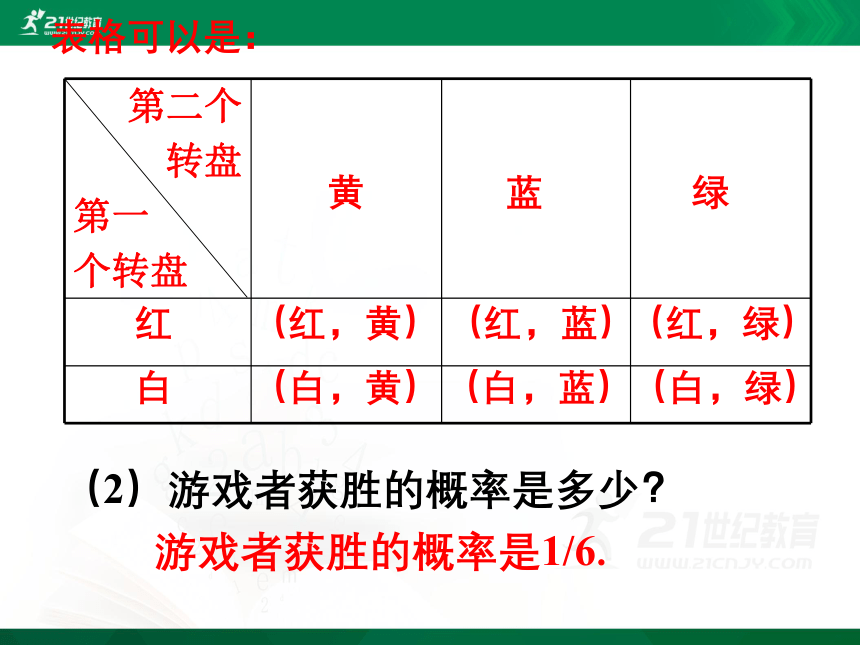
表格可以是:
第二个
转盘
第一
个转盘
黄
蓝
绿
红
(红,黄)
(红,蓝)
(红,绿)
白
(白,黄)
(白,蓝)
(白,绿)
(2)游戏者获胜的概率是多少?
游戏者获胜的概率是1/6.
问题探讨:
随机事件在一次试验中是否发生虽然不能事先确定,但是在大量重复试验的情况下,它的发生是否会呈现出一定的规律性呢?
试验
每人抛掷硬币10次,
计算出正面向上的频率.
大家一起来掷硬币
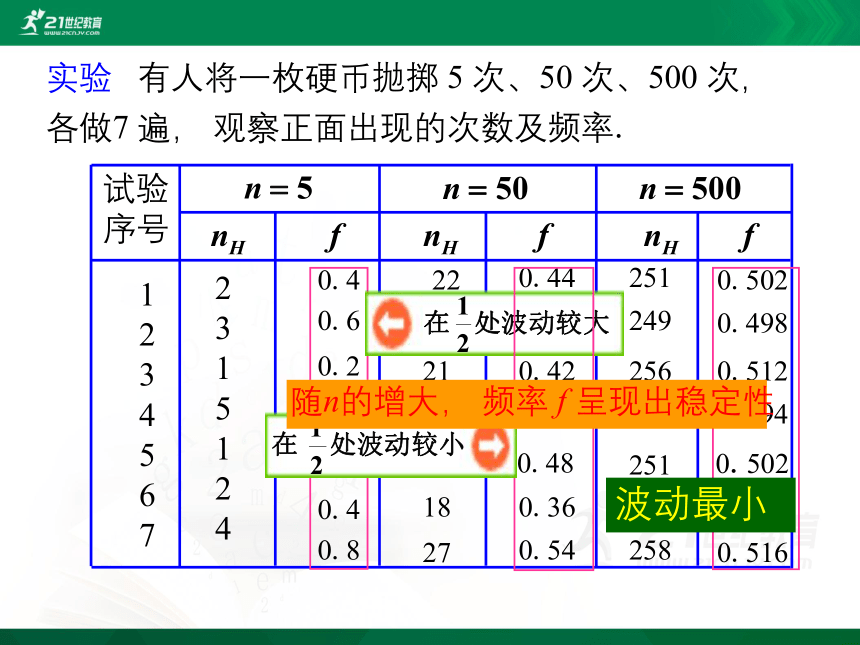
实验 有人将一枚硬币抛掷 5 次、50 次、500 次, 各做7 遍, 观察正面出现的次数及频率.
试验
序号
22
25
21
25
24
18
27
251
249
256
247
251
262
258
0.4
0.6
0.2
1.0
0.2
0.4
0.8
0.44
0.50
0.42
0.48
0.36
0.54
0.502
0.498
0.512
0.494
0.524
0.516
0.50
0.502
波动最小
随n的增大, 频率 f 呈现出稳定性
1
2
3
4
5
6
7
2
3
1
5
1
2
4
抛掷次数(n)
2048
4040
12000
24000
30000
正面朝上次数(m)
1061
2048
6019
12012
14984
频率(m/n)
0.518
0.506
0.501
0.5005
0.4996
历史上曾有人作过抛掷硬币的大量重复实验,结果如下表所示
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
72088
德 . 摩根
蒲 丰
皮尔逊
皮尔逊
维 尼
总结归纳
一、事件A的概率:
一般地,在大量重复进行同一试验时,事件A发生的频率 总是接近于某个常数,在它附近摆动,这时就把这个常数叫做A事件的概率,记作P(A).
(1) 只有当频率在某个常数附近摆动时,这个常数才叫 做事件A的概率;
(2)概率是反映事件发生的可能性大小的量;(意义)
(3)概率的性质:必然事件的概率是1,不可能事件的概率是0.事件A的概率是0≤P(A) ≦1 .
注意:
思考:事件A发生的频率fn(A)是不是不变的?事件A发生的概率P(A)是不是不变的?它们之间有什么区别和联系?
1、频率本身是随机的,在试验前不能确定.做同样次数的重复试验得到事件的频率会不同.
2、概率是一个确定的数,与每次试验无关.是用来度量事件发生可能性大小的量.
3、随着试验次数的增加,频率在概率的附近摆动并趋于稳定,实际问题中,用频率接近的常数作为概率的估计值
二、频率与概率的联系与区别
(1)频率本身是随机变化的,具有随机性,
试验前不能确定.
(2)概率是一个确定的数,客观存在的,与试验次数无关.
频率是概率的近似值,概率是频率的稳定值.
联系:
区别:
(由频率估算出概率)
例题:对某电视机厂生产的电视机进行抽样检测的数据如下:
(1)计算表中优等品的各个频率;
(2)该厂生产的电视机优等品的概率是多少?
优等品频率( )
954
478
285
192
92
40
优等品数(m)
1000
500
300
200
100
50
抽取台数(n)
0.8
0.92
0.96
0.95
0.956
0.954
n
m
0.9
1.某射手在同一条件下进行射击,结果如下表所示:
射击次数(n)
10
20
50
100
200
500
击中靶心次数(m)
9
19
44
91
178
451
击中靶心频率( )
(1)计算表中击中靶心的各个频率;
(2)这个射手射击一次,击中靶心的概率约是多少?
0.9
0.95
0.88
0.91
0.88
0.90
0.9
问:该射击手击中靶心的概率为90%,那他再射击10次,一定会命中9次吗?
不一定,射击10次,相当于10次试验,试验具有随机性,命中9次是随机事件.
1、随机事件在n次试验中发生了m次,则( )
(A) 0<m<n (B) 0<n<m
(C) 0≤m≤n (D) 0≤n≤m
2.下列结论正确的是( )
A.对于事件的概率,必有0B.不可能事件的频率为0;
C.随机事件的频率大于0;
D.事件A的概率P(A)=0.9999,则件A是必然事件;
B
C
随堂训练
3、 盒中装有4个白球5个黑球,从中任意的取出一个球.
(1)“取出的是黄球”是什么事件?概率是多少?
(2)“取出的是白球”是什么事件?概率是多少?
(3)“取出的是白球或者是黑球”是什么事件?概率是多少?
是不可能事件,概率是0
是随机事件,概率是4/9
是必然事件,概率是1
如果某种彩票的中奖概率为1/1000,那么买1000张这种彩票一定能中奖吗?
解:买1000张彩票相当于1000次试验,对于一次试验来说,其结果是随机的,即有可能中奖,也有可能不中奖,但这种随机性又呈现一定的规律性,“彩票的中奖概率为1/1000是指当试验次数相当大,即随着购买彩票的张数的增加,大约有1/1000的彩票中奖.因此,买1000张彩票,即做1000次试验,其结果仍是随机的,可能一次也没有中奖,也可能中奖一次、二次、甚至多次.
思考讨论
P=1-0.9991000≈0.632
1.若用上例这种小麦种子350g播种,大约能得到多少棵麦苗?
2.任意抛掷一枚均匀的骰子,朝上面的点数为1的概率为 .下列说法正确吗?为什么?
(1)任意抛掷一枚均匀的骰子12次,朝上面的点数为1的次数为2次.
(2)任意抛掷一枚均匀的骰子1200次,朝上面的点数为1的次数大约为200次.
课后练习:
解:
1. 350×0.95≈333(棵)
答:大约能得到333棵麦苗
2.(1)不正确,因为抛掷的次数较少,不能很好的用频率估计概率.
(2)正确,因为抛掷次数较多,可以用频率近似估计概率.
3.某运动员投篮5次,投中4次.能否说该运动员投1次篮,投中的概率为 ?为什么?
2.美国密歇根州汉诺市的一个农场里出生了一头白色的小奶牛.据统计,平均出生1000万头牛才会有1头是白色的.由此估计出生1头白色奶牛的概率是多少?
解:1.不能,因为投篮次数太少,不能用此事件发生的频率去估计概率.
P=
答:出生1头白色奶牛的概率是 .
谢谢聆听
8.3 频率与概率
第8章 认识概率
2020-2021学年度苏科版八年级下册
(1)海枯石烂
(2)守株待兔
随机事件
不可能事件
(3)水中捞月
不可能事件
(4)种瓜得瓜,种豆得豆.
必然事件
2:在下列词语中,那些是刻画必然事件的,那些是刻画不可能事件的,那些是刻画随机事件的?
1.随机事件、必然事件、不可能事件的定义分别是什么?
知识回顾:
频率:在n次重复试验, 事件A发生了m次(0≦m ≦n) m叫做事件A的频数, 事件A的频数在实验的总次数中的比例 ,叫做事件A出现的频率.
(2)频率的范围:
(3)频率是随机的,在试验前不确定的,就算做同样次数的试验频率都可能不同.
n
m
3、频率的定义是什么?
n
m
A
f
n
=
)
(
理解:
(1)记作:
小颖为学校联欢会设计了一个“配紫色”的游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起就配成了紫色.
(1)利用树状图或列表的方法表示游戏所有可能出现的结果.
树状图可以是:
开始
红
白
黄
蓝
绿
(红,黄)
(红,蓝)
(红,绿)
(白,黄)
(白,蓝)
(白,绿)
黄
蓝
绿
表格可以是:
第二个
转盘
第一
个转盘
黄
蓝
绿
红
(红,黄)
(红,蓝)
(红,绿)
白
(白,黄)
(白,蓝)
(白,绿)
(2)游戏者获胜的概率是多少?
游戏者获胜的概率是1/6.
问题探讨:
随机事件在一次试验中是否发生虽然不能事先确定,但是在大量重复试验的情况下,它的发生是否会呈现出一定的规律性呢?
试验
每人抛掷硬币10次,
计算出正面向上的频率.
大家一起来掷硬币
实验 有人将一枚硬币抛掷 5 次、50 次、500 次, 各做7 遍, 观察正面出现的次数及频率.
试验
序号
22
25
21
25
24
18
27
251
249
256
247
251
262
258
0.4
0.6
0.2
1.0
0.2
0.4
0.8
0.44
0.50
0.42
0.48
0.36
0.54
0.502
0.498
0.512
0.494
0.524
0.516
0.50
0.502
波动最小
随n的增大, 频率 f 呈现出稳定性
1
2
3
4
5
6
7
2
3
1
5
1
2
4
抛掷次数(n)
2048
4040
12000
24000
30000
正面朝上次数(m)
1061
2048
6019
12012
14984
频率(m/n)
0.518
0.506
0.501
0.5005
0.4996
历史上曾有人作过抛掷硬币的大量重复实验,结果如下表所示
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
72088
德 . 摩根
蒲 丰
皮尔逊
皮尔逊
维 尼
总结归纳
一、事件A的概率:
一般地,在大量重复进行同一试验时,事件A发生的频率 总是接近于某个常数,在它附近摆动,这时就把这个常数叫做A事件的概率,记作P(A).
(1) 只有当频率在某个常数附近摆动时,这个常数才叫 做事件A的概率;
(2)概率是反映事件发生的可能性大小的量;(意义)
(3)概率的性质:必然事件的概率是1,不可能事件的概率是0.事件A的概率是0≤P(A) ≦1 .
注意:
思考:事件A发生的频率fn(A)是不是不变的?事件A发生的概率P(A)是不是不变的?它们之间有什么区别和联系?
1、频率本身是随机的,在试验前不能确定.做同样次数的重复试验得到事件的频率会不同.
2、概率是一个确定的数,与每次试验无关.是用来度量事件发生可能性大小的量.
3、随着试验次数的增加,频率在概率的附近摆动并趋于稳定,实际问题中,用频率接近的常数作为概率的估计值
二、频率与概率的联系与区别
(1)频率本身是随机变化的,具有随机性,
试验前不能确定.
(2)概率是一个确定的数,客观存在的,与试验次数无关.
频率是概率的近似值,概率是频率的稳定值.
联系:
区别:
(由频率估算出概率)
例题:对某电视机厂生产的电视机进行抽样检测的数据如下:
(1)计算表中优等品的各个频率;
(2)该厂生产的电视机优等品的概率是多少?
优等品频率( )
954
478
285
192
92
40
优等品数(m)
1000
500
300
200
100
50
抽取台数(n)
0.8
0.92
0.96
0.95
0.956
0.954
n
m
0.9
1.某射手在同一条件下进行射击,结果如下表所示:
射击次数(n)
10
20
50
100
200
500
击中靶心次数(m)
9
19
44
91
178
451
击中靶心频率( )
(1)计算表中击中靶心的各个频率;
(2)这个射手射击一次,击中靶心的概率约是多少?
0.9
0.95
0.88
0.91
0.88
0.90
0.9
问:该射击手击中靶心的概率为90%,那他再射击10次,一定会命中9次吗?
不一定,射击10次,相当于10次试验,试验具有随机性,命中9次是随机事件.
1、随机事件在n次试验中发生了m次,则( )
(A) 0<m<n (B) 0<n<m
(C) 0≤m≤n (D) 0≤n≤m
2.下列结论正确的是( )
A.对于事件的概率,必有0
C.随机事件的频率大于0;
D.事件A的概率P(A)=0.9999,则件A是必然事件;
B
C
随堂训练
3、 盒中装有4个白球5个黑球,从中任意的取出一个球.
(1)“取出的是黄球”是什么事件?概率是多少?
(2)“取出的是白球”是什么事件?概率是多少?
(3)“取出的是白球或者是黑球”是什么事件?概率是多少?
是不可能事件,概率是0
是随机事件,概率是4/9
是必然事件,概率是1
如果某种彩票的中奖概率为1/1000,那么买1000张这种彩票一定能中奖吗?
解:买1000张彩票相当于1000次试验,对于一次试验来说,其结果是随机的,即有可能中奖,也有可能不中奖,但这种随机性又呈现一定的规律性,“彩票的中奖概率为1/1000是指当试验次数相当大,即随着购买彩票的张数的增加,大约有1/1000的彩票中奖.因此,买1000张彩票,即做1000次试验,其结果仍是随机的,可能一次也没有中奖,也可能中奖一次、二次、甚至多次.
思考讨论
P=1-0.9991000≈0.632
1.若用上例这种小麦种子350g播种,大约能得到多少棵麦苗?
2.任意抛掷一枚均匀的骰子,朝上面的点数为1的概率为 .下列说法正确吗?为什么?
(1)任意抛掷一枚均匀的骰子12次,朝上面的点数为1的次数为2次.
(2)任意抛掷一枚均匀的骰子1200次,朝上面的点数为1的次数大约为200次.
课后练习:
解:
1. 350×0.95≈333(棵)
答:大约能得到333棵麦苗
2.(1)不正确,因为抛掷的次数较少,不能很好的用频率估计概率.
(2)正确,因为抛掷次数较多,可以用频率近似估计概率.
3.某运动员投篮5次,投中4次.能否说该运动员投1次篮,投中的概率为 ?为什么?
2.美国密歇根州汉诺市的一个农场里出生了一头白色的小奶牛.据统计,平均出生1000万头牛才会有1头是白色的.由此估计出生1头白色奶牛的概率是多少?
解:1.不能,因为投篮次数太少,不能用此事件发生的频率去估计概率.
P=
答:出生1头白色奶牛的概率是 .
谢谢聆听
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
