9.1 图形的旋转(第2课时) 课件(共31张PPT)
文档属性
| 名称 | 9.1 图形的旋转(第2课时) 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 00:00:00 | ||
图片预览








文档简介
9.1 图形的旋转
第9章 中心对称图形——平行四边形
第2课时
2020-2021学年度苏科版八年级下册
你喜欢到游乐园玩吗?
议一议
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?
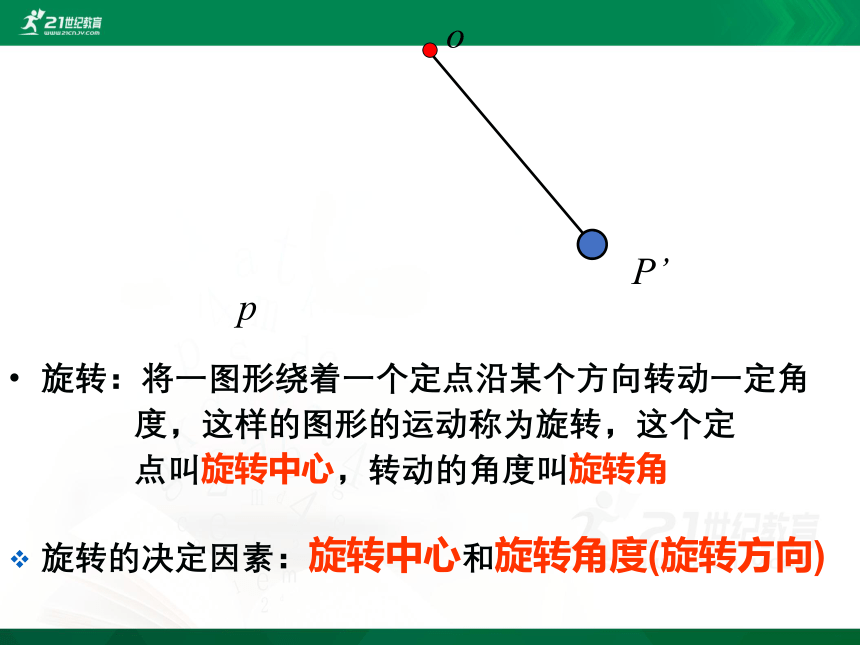
p
P’
o
旋转:将一图形绕着一个定点沿某个方向转动一定角
度,这样的图形的运动称为旋转,这个定
点叫旋转中心,转动的角度叫旋转角
旋转的决定因素:旋转中心和旋转角度(旋转方向)
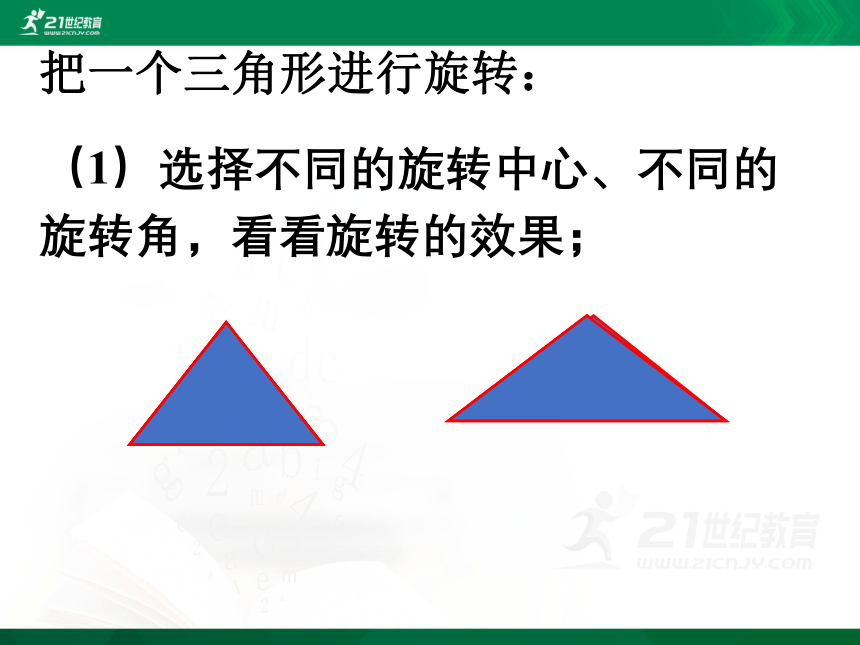
把一个三角形进行旋转:
(1)选择不同的旋转中心、不同的旋转角,看看旋转的效果;
(2)改变三角形的形状,看看旋转的效果.
1.如图,正方形 是正方形ABCD按顺时针方向选择一定的角度而得到的.请指出图中哪一点是旋转中心,并度量旋转角的度数.
答:旋转中心是A点;旋转角大约为45°
A(A′)
B
C
D
D′
C′
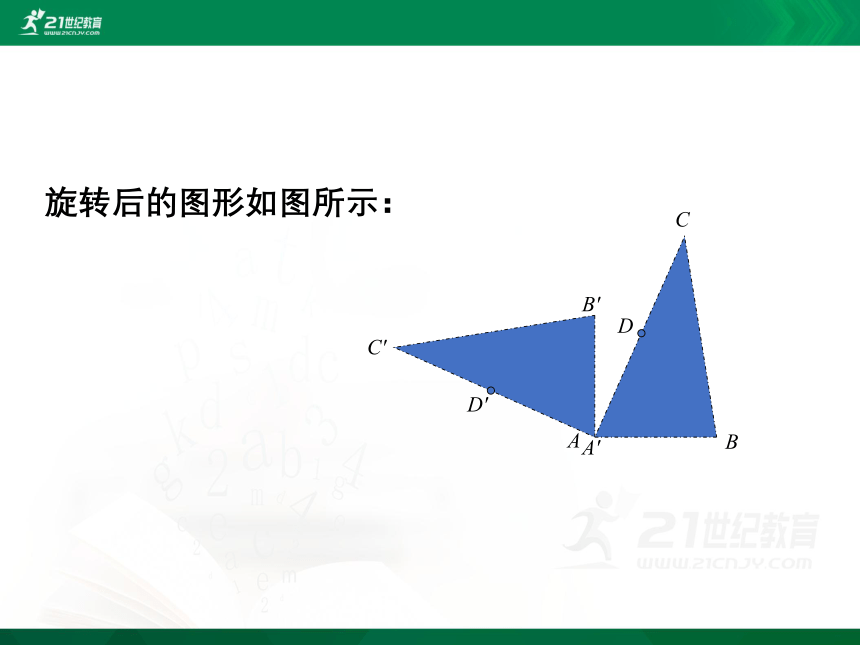
2.如图,D是AC的中点,画出△ABC绕点A按逆时针方向旋转90°所得到的三角形,以及点D的对应点D′.
C
A
B
D
C
A
B
D
C′
A′
B′
D′
旋转后的图形如图所示:
(4)对应点到旋转中心的距离相等.
旋转的基本性质
(1)旋转不改变图形的大小和形状.
(2)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度
(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角.
平移和旋转的异同:
1、相同:都是一种运动;运动前后 不改变图形的形状和大小
B
A
C
O
2、不同
运动方向
运动量的衡量
平移
直线
移动一定距离
旋转
顺时针、逆时针
转动一定的角度
可以看作是一个花瓣连续4次旋转所形成的,每次旋转分别等于720 , 1440 , 2160 , 2880
思考题:香港区徽可以看作是什么“基本图案”通过怎样的旋转而得到的?
A
O
B
A’
B’
45°
点B的对应点是___;线段OB的对应线段是线段___;线段AB的对应线段是线段___;∠A的对应角是___;∠B的对应角是___;旋转中心是点___;旋转的角度是___。
问题一
C
B
A
A’
B’
C’
O
如图,将△ ABC绕着外面的点O旋转60°将整个△ ABC旋转到△A’B’C’的位置。
点B的对应点是___;线段BC的对应线段是线段___;线段AB的对应线段是线段___;∠C的对应角是___;∠B的对应角是___;旋转中心是点___;旋转的角度是___
问题二
D
E
F
C
B
A
O
如图, △ DEF是由△ ABC绕点O旋转得到的,你能说出其中的对应点、对应角和对应线段吗?
问题三
1、如图,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3) 如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
解:(1)旋转中心是A
(2)旋转了60°
(3)点M转到了AC 的中点位置上
2、如图,△ABC和 △ ADE都是等腰直角三角形, ∠ C和∠ AED都是直角,点E在AB上,如果△ABC经旋转后能与△ ADE重合,那么哪一点是旋转中心?旋转了多少度?
A
C
B
D
E
试一试
图中是否存在这样的两个三角形,其中一个是通过另一个旋转得到的?
钟表的指针在不停地转动,如图,从3时到5时,时针转动了多少度?
如图,风车风轮的每个叶片在风的吹动下转到新的位置.以上这些现象有什么共同特点呢?
12
6
1
2
3
4
5
7
8
9
10
11
时针转动了60°.
以上现象的共同特点是:物体绕定点转动.
简单的旋转作图
项目
已知
未知
备注
源图形
●
点A
源位置
●
点A
旋转中心
●
点O
旋转方向
●
顺时针
旋转角度
●
60?
目标图形
●
点
目标位置
●
点B (求作)
A
O
点的旋转作法
课外例1 将A点绕O点沿顺时针方向旋转60?.
分析:
作法:
1. 以点O为圆心,OA长为半径画圆;
2. 连接OA, 用量角器或三角板(限
特殊角)作出∠AOB,与圆周交
于B点;
3. B点即为所求作.
B
简单的旋转作图
项目
已知
未知
备注
源图形
●
线段AB
源位置
●
线段AB
旋转中心
●
点O
旋转方向
●
顺时针
旋转角度
●
60?
目标图形
●
线段
目标位置
●
线段CD (求作)
A
O
线段的旋转作法
课外例2 将线段AB绕O点沿顺时针方向旋转60?.
分析:
作法:
将点A绕点O顺时针旋转60?,得
点C;
2. 将点B绕点O顺时针旋转60 ?,得点D ;
3. 连接CD, 则线段CD即为所求作.
C
B
D
简单的旋转作图
项目
已知
未知
备注
源图形
●
△ABC
源位置
●
△ABC
旋转中心
●
点C
旋转方向
●
根据A与D的对应关系判断为顺时针
旋转角度
●
∠ACD
目标图形
●
三角形
目标位置
●
△DEC (求作)
图形的旋转作法
课外例3 如图,△ABC绕C点旋转后,顶点A得对应点为点D. 试确定顶点B对应点的位置以及旋转后的三角形.
分析:
作法一:
1. 连接CD;
2. 以CB为一边,作∠BCE,使得∠BCE=∠ACD ;
3. 在射线CB上截取CE,使得CE=CB;
4. 连接DE,则△DEC即为所求作.
C
A
B
D
E
简单的旋转作图
练习1
将下图中大写字母N绕它右下侧的顶点按顺时针方向旋转90?,作出旋转后的图案.
引申1:如图,它是由哪个“图案”通过旋转得到的?旋转中心在何处?旋转了多少度?
?
???????????????????????????????????????????????
?
?
思考:本答案唯一吗?共有几种不同的旋转方式?
引申2:如图,△ABE和△ACD均为直角三角形,∠EAB=∠CAD=900,连结EC,
???????画出△ACE以点A为旋转中心逆时针方向旋转900后的三角形.
??????????????????????????????????????????????????????????
?
??
探索发现
联系前面所学内容,我们应如何探索出旋转所具有的特征?
A
B
C
D
E
E′
解:因为点A是旋转中心,所以它的对应点是它本身.
正方形ABCD中,AD=AB, ∠DAB=90°,所以旋转后点D与B重合.
如图,E是正方形ABCD中CD边上的一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
边AE以点A为中心,旋转90 °,所以过点A做直线AE′垂直于AE交BC的延长线于点E′.
则△ADE′为旋转后的图形.
课堂回顾:这节课,主要学习了什么?
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转
旋转的概念:
旋转的性质:
1、旋转不改变图形的大小和形状.
2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角,旋转角相等.
3、对应点到旋转中心的距离相等
谢谢聆听
第9章 中心对称图形——平行四边形
第2课时
2020-2021学年度苏科版八年级下册
你喜欢到游乐园玩吗?
议一议
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?
p
P’
o
旋转:将一图形绕着一个定点沿某个方向转动一定角
度,这样的图形的运动称为旋转,这个定
点叫旋转中心,转动的角度叫旋转角
旋转的决定因素:旋转中心和旋转角度(旋转方向)
把一个三角形进行旋转:
(1)选择不同的旋转中心、不同的旋转角,看看旋转的效果;
(2)改变三角形的形状,看看旋转的效果.
1.如图,正方形 是正方形ABCD按顺时针方向选择一定的角度而得到的.请指出图中哪一点是旋转中心,并度量旋转角的度数.
答:旋转中心是A点;旋转角大约为45°
A(A′)
B
C
D
D′
C′
2.如图,D是AC的中点,画出△ABC绕点A按逆时针方向旋转90°所得到的三角形,以及点D的对应点D′.
C
A
B
D
C
A
B
D
C′
A′
B′
D′
旋转后的图形如图所示:
(4)对应点到旋转中心的距离相等.
旋转的基本性质
(1)旋转不改变图形的大小和形状.
(2)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度
(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角.
平移和旋转的异同:
1、相同:都是一种运动;运动前后 不改变图形的形状和大小
B
A
C
O
2、不同
运动方向
运动量的衡量
平移
直线
移动一定距离
旋转
顺时针、逆时针
转动一定的角度
可以看作是一个花瓣连续4次旋转所形成的,每次旋转分别等于720 , 1440 , 2160 , 2880
思考题:香港区徽可以看作是什么“基本图案”通过怎样的旋转而得到的?
A
O
B
A’
B’
45°
点B的对应点是___;线段OB的对应线段是线段___;线段AB的对应线段是线段___;∠A的对应角是___;∠B的对应角是___;旋转中心是点___;旋转的角度是___。
问题一
C
B
A
A’
B’
C’
O
如图,将△ ABC绕着外面的点O旋转60°将整个△ ABC旋转到△A’B’C’的位置。
点B的对应点是___;线段BC的对应线段是线段___;线段AB的对应线段是线段___;∠C的对应角是___;∠B的对应角是___;旋转中心是点___;旋转的角度是___
问题二
D
E
F
C
B
A
O
如图, △ DEF是由△ ABC绕点O旋转得到的,你能说出其中的对应点、对应角和对应线段吗?
问题三
1、如图,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3) 如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
解:(1)旋转中心是A
(2)旋转了60°
(3)点M转到了AC 的中点位置上
2、如图,△ABC和 △ ADE都是等腰直角三角形, ∠ C和∠ AED都是直角,点E在AB上,如果△ABC经旋转后能与△ ADE重合,那么哪一点是旋转中心?旋转了多少度?
A
C
B
D
E
试一试
图中是否存在这样的两个三角形,其中一个是通过另一个旋转得到的?
钟表的指针在不停地转动,如图,从3时到5时,时针转动了多少度?
如图,风车风轮的每个叶片在风的吹动下转到新的位置.以上这些现象有什么共同特点呢?
12
6
1
2
3
4
5
7
8
9
10
11
时针转动了60°.
以上现象的共同特点是:物体绕定点转动.
简单的旋转作图
项目
已知
未知
备注
源图形
●
点A
源位置
●
点A
旋转中心
●
点O
旋转方向
●
顺时针
旋转角度
●
60?
目标图形
●
点
目标位置
●
点B (求作)
A
O
点的旋转作法
课外例1 将A点绕O点沿顺时针方向旋转60?.
分析:
作法:
1. 以点O为圆心,OA长为半径画圆;
2. 连接OA, 用量角器或三角板(限
特殊角)作出∠AOB,与圆周交
于B点;
3. B点即为所求作.
B
简单的旋转作图
项目
已知
未知
备注
源图形
●
线段AB
源位置
●
线段AB
旋转中心
●
点O
旋转方向
●
顺时针
旋转角度
●
60?
目标图形
●
线段
目标位置
●
线段CD (求作)
A
O
线段的旋转作法
课外例2 将线段AB绕O点沿顺时针方向旋转60?.
分析:
作法:
将点A绕点O顺时针旋转60?,得
点C;
2. 将点B绕点O顺时针旋转60 ?,得点D ;
3. 连接CD, 则线段CD即为所求作.
C
B
D
简单的旋转作图
项目
已知
未知
备注
源图形
●
△ABC
源位置
●
△ABC
旋转中心
●
点C
旋转方向
●
根据A与D的对应关系判断为顺时针
旋转角度
●
∠ACD
目标图形
●
三角形
目标位置
●
△DEC (求作)
图形的旋转作法
课外例3 如图,△ABC绕C点旋转后,顶点A得对应点为点D. 试确定顶点B对应点的位置以及旋转后的三角形.
分析:
作法一:
1. 连接CD;
2. 以CB为一边,作∠BCE,使得∠BCE=∠ACD ;
3. 在射线CB上截取CE,使得CE=CB;
4. 连接DE,则△DEC即为所求作.
C
A
B
D
E
简单的旋转作图
练习1
将下图中大写字母N绕它右下侧的顶点按顺时针方向旋转90?,作出旋转后的图案.
引申1:如图,它是由哪个“图案”通过旋转得到的?旋转中心在何处?旋转了多少度?
?
???????????????????????????????????????????????
?
?
思考:本答案唯一吗?共有几种不同的旋转方式?
引申2:如图,△ABE和△ACD均为直角三角形,∠EAB=∠CAD=900,连结EC,
???????画出△ACE以点A为旋转中心逆时针方向旋转900后的三角形.
??????????????????????????????????????????????????????????
?
??
探索发现
联系前面所学内容,我们应如何探索出旋转所具有的特征?
A
B
C
D
E
E′
解:因为点A是旋转中心,所以它的对应点是它本身.
正方形ABCD中,AD=AB, ∠DAB=90°,所以旋转后点D与B重合.
如图,E是正方形ABCD中CD边上的一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
边AE以点A为中心,旋转90 °,所以过点A做直线AE′垂直于AE交BC的延长线于点E′.
则△ADE′为旋转后的图形.
课堂回顾:这节课,主要学习了什么?
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转
旋转的概念:
旋转的性质:
1、旋转不改变图形的大小和形状.
2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角,旋转角相等.
3、对应点到旋转中心的距离相等
谢谢聆听
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
