9.2 中心对称与中心对称图形(第1课时) 课件(共27张PPT)
文档属性
| 名称 | 9.2 中心对称与中心对称图形(第1课时) 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 380.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 19:48:23 | ||
图片预览




文档简介
(共25张PPT)
9.2 中心对称与中心对称图形
第1课时
第9章 中心对称图形——平行四边形
2020-2021学年度苏科版八年级下册
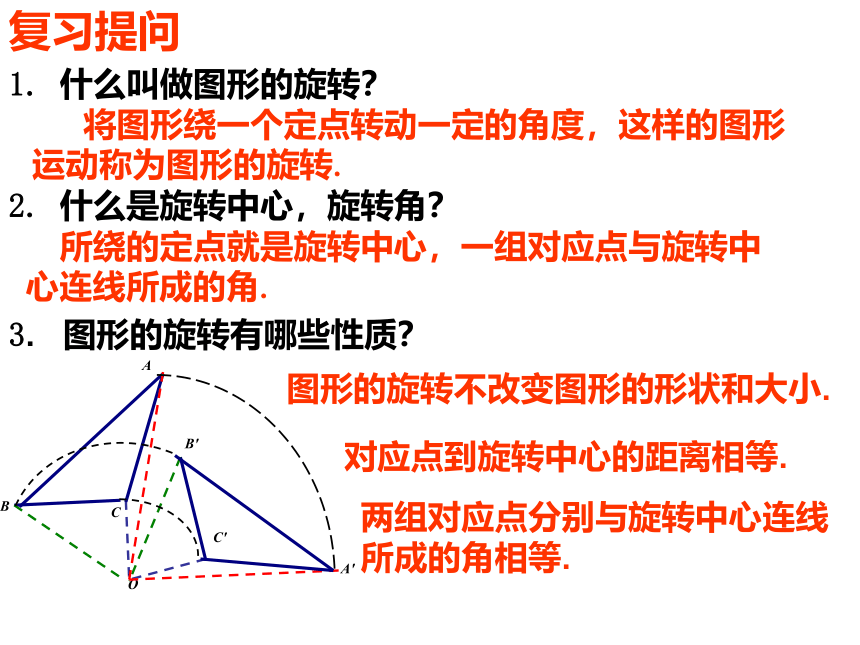
1. 什么叫做图形的旋转?
2. 什么是旋转中心,旋转角?
3. 图形的旋转有哪些性质?
B'
O
A'
C'
B
A
C
复习提问
将图形绕一个定点转动一定的角度,这样的图形运动称为图形的旋转.
所绕的定点就是旋转中心,一组对应点与旋转中心连线所成的角.
图形的旋转不改变图形的形状和大小.
对应点到旋转中心的距离相等.
两组对应点分别与旋转中心连线所成的角相等.
情境创设
“双鱼”剪纸作品是由两个形状、大小完全相同的图案组成的,这两个图案的位置有怎样的特殊关系?怎样改变其中一个图案的位置,可以使它与另一个图案重合?
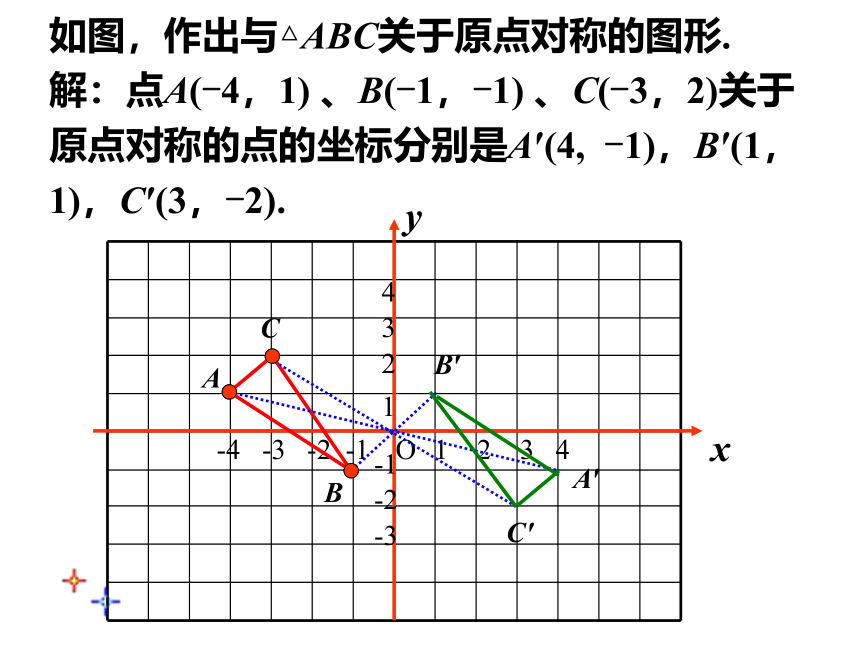
如图,作出与△ABC关于原点对称的图形.
x
y
O
-4 -3 -2 -1 1 2 3 4
-1
2
3
4
1
-2
-3
A
解:点A(-4,1) 、B(-1,-1) 、C(-3,2)关于原点对称的点的坐标分别是A′(4, -1),B′(1, 1),C′(3,-2).
C
B
A′
B′
C′
上图所示的两个三角形便是中心对称图形,所以你可以类比轴对称图形说出中心对称图形有什么特点,怎样做出中心对称图形,生活中有哪些中心对称的实例也可以交流一下.
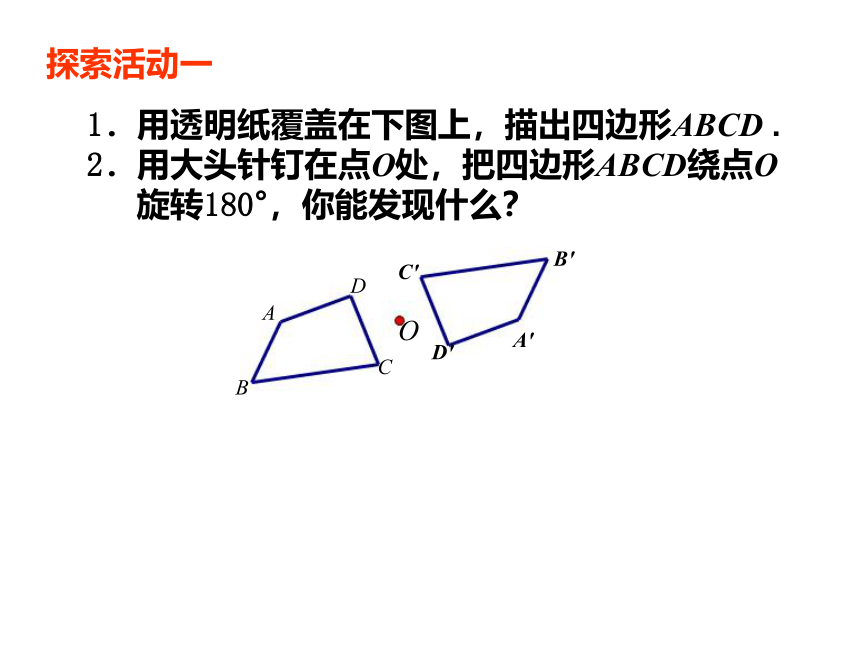
探索活动一
1.用透明纸覆盖在下图上,描出四边形ABCD .
2.用大头针钉在点O处,把四边形ABCD绕点O
旋转180°,你能发现什么?
O
A
B
C
D
A′
B′
C′
D′
O
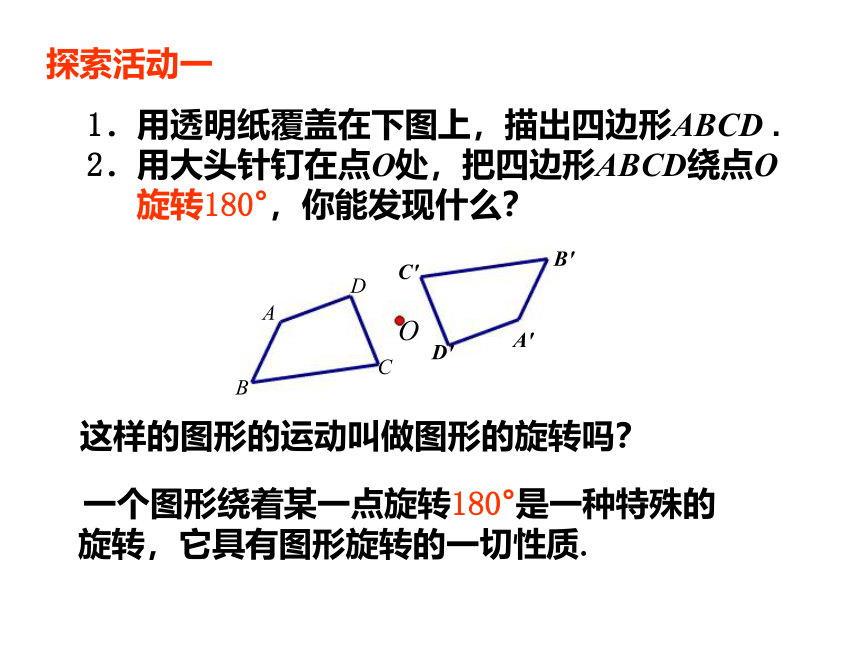
探索活动一
1.用透明纸覆盖在下图上,描出四边形ABCD .
2.用大头针钉在点O处,把四边形ABCD绕点O
旋转180°,你能发现什么?
O
A
B
C
D
A′
B′
C′
D′
O
这样的图形的运动叫做图形的旋转吗?
一个图形绕着某一点旋转180°是一种特殊的旋转,它具有图形旋转的一切性质.
探索活动一
1.用透明纸覆盖在下图上,描出四边形ABCD .
2.用大头针钉在点O处,把四边形ABCD绕点O
旋转180°,你能发现什么?
O
A
B
C
D
A′
B′
C′
D′
O
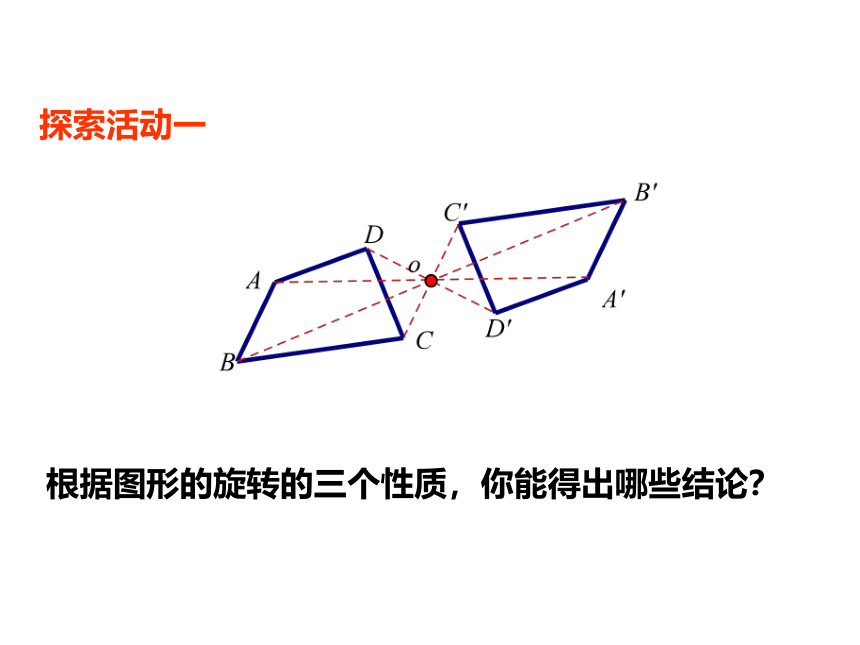
根据图形的旋转的三个性质,你能得出哪些结论?
探索活动一
根据图形的旋转的三个性质,你能得出哪些结论?
探索活动一
一个图形绕着某一点旋转180 °,如果它能够与另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称.这个点叫做对称中心.
O
A
B
C
D
A′
B′
C′
D′
O
探索活动二
1.如图,点A与点A′关于点O对称,连接AA′,你能发现什么?
A
A′
O
2.在图中分别连接AA′、BB′、CC′、DD′,你发现了什么?
探索活动二
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
探索活动三
1.已知点A和O,你能画出点A关于点O的对称点吗?
探索活动三
2.已知线段AB和O点,你能画出线段AB关于点O的对称线段吗?
探索活动三
3.已知△ABC和点O,你能画出△ABC关于O成中心对称的图形吗?
在如图所示的四张扑克牌中,你认为哪一张的牌面是中心对称图形?是中心对称图形的,找出它的对称中心.
解:方块5、黑桃Q和花子8的牌面是中心对称图形.
对称中心分别为牌面的两对角线交点.
练习:
如图,已知△ABC与△A′B′C′中心对称,
求出它们的对称中心O.
A
B
C
A′
B′
C′
巩固练习
解法一:根据观察,B、B′应是对应点,连结
BB′,用刻度尺找出BB′的中点O,
则点O即为所求(如图)
A
B
C
A′
B′
C ′
O
O
解法二:根据观察,B、B′及C、C ′应分别是两
组对应点,连结BB′ 、CC′ ,它们相
交于点O,则点O即为所求(如图).
A
B
C
A′
B′
C′
探索活动四
观察下列图案说一说它们有什么共同特征?
在日常生活中,你还见到过具有这种特征的图案吗?试举例说明.
把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形互相重合,那么这个图形叫做中心对称图形.这个点就是它的对称中心.
中心对称与轴对称有什么区别 又有什么联系
轴对称 中心对称
有一条对称轴——直线 有一个对称中心——点
图形沿对称轴对折(翻折180°)后重合 图形绕对称中心旋转180°后重合
折叠后与另一图形重合 旋转后与另一图形重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
探索活动五
我们知道,轴对称与轴对称图形既有联系又有区别.
1.如图,在△ABC中,O是AC的中点,画△ABC关于点O对称的△A′B′C′.
A
B
C
O
(A′)
B′
(C′)
(O′)
2.线段是中心对称图形吗?如果是,说出它的对称中心.
答:线段是中心对称图形,对称中心既是线段中点.
3.在正方形的4个角上剪去4个相同的小正方形(如图),剩余部分是中心对称图形吗?如果是,画出它的对称中心.
O
答:是中心对称图形,O既是对称中心.
轴对称 中心对称
有一条对称轴——直线 有一个对称中心——点
图形沿对称轴对折(翻折180°)后重合 图形绕对称中心旋转180°后重合
折叠后与另一图形重合 旋转后与另一图形重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
课堂小结
1.一个图形绕着某一点旋转180 °,如果它能够与另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称.这个点叫做对称中心.
2.成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
谢谢聆听
9.2 中心对称与中心对称图形
第1课时
第9章 中心对称图形——平行四边形
2020-2021学年度苏科版八年级下册
1. 什么叫做图形的旋转?
2. 什么是旋转中心,旋转角?
3. 图形的旋转有哪些性质?
B'
O
A'
C'
B
A
C
复习提问
将图形绕一个定点转动一定的角度,这样的图形运动称为图形的旋转.
所绕的定点就是旋转中心,一组对应点与旋转中心连线所成的角.
图形的旋转不改变图形的形状和大小.
对应点到旋转中心的距离相等.
两组对应点分别与旋转中心连线所成的角相等.
情境创设
“双鱼”剪纸作品是由两个形状、大小完全相同的图案组成的,这两个图案的位置有怎样的特殊关系?怎样改变其中一个图案的位置,可以使它与另一个图案重合?
如图,作出与△ABC关于原点对称的图形.
x
y
O
-4 -3 -2 -1 1 2 3 4
-1
2
3
4
1
-2
-3
A
解:点A(-4,1) 、B(-1,-1) 、C(-3,2)关于原点对称的点的坐标分别是A′(4, -1),B′(1, 1),C′(3,-2).
C
B
A′
B′
C′
上图所示的两个三角形便是中心对称图形,所以你可以类比轴对称图形说出中心对称图形有什么特点,怎样做出中心对称图形,生活中有哪些中心对称的实例也可以交流一下.
探索活动一
1.用透明纸覆盖在下图上,描出四边形ABCD .
2.用大头针钉在点O处,把四边形ABCD绕点O
旋转180°,你能发现什么?
O
A
B
C
D
A′
B′
C′
D′
O
探索活动一
1.用透明纸覆盖在下图上,描出四边形ABCD .
2.用大头针钉在点O处,把四边形ABCD绕点O
旋转180°,你能发现什么?
O
A
B
C
D
A′
B′
C′
D′
O
这样的图形的运动叫做图形的旋转吗?
一个图形绕着某一点旋转180°是一种特殊的旋转,它具有图形旋转的一切性质.
探索活动一
1.用透明纸覆盖在下图上,描出四边形ABCD .
2.用大头针钉在点O处,把四边形ABCD绕点O
旋转180°,你能发现什么?
O
A
B
C
D
A′
B′
C′
D′
O
根据图形的旋转的三个性质,你能得出哪些结论?
探索活动一
根据图形的旋转的三个性质,你能得出哪些结论?
探索活动一
一个图形绕着某一点旋转180 °,如果它能够与另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称.这个点叫做对称中心.
O
A
B
C
D
A′
B′
C′
D′
O
探索活动二
1.如图,点A与点A′关于点O对称,连接AA′,你能发现什么?
A
A′
O
2.在图中分别连接AA′、BB′、CC′、DD′,你发现了什么?
探索活动二
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
探索活动三
1.已知点A和O,你能画出点A关于点O的对称点吗?
探索活动三
2.已知线段AB和O点,你能画出线段AB关于点O的对称线段吗?
探索活动三
3.已知△ABC和点O,你能画出△ABC关于O成中心对称的图形吗?
在如图所示的四张扑克牌中,你认为哪一张的牌面是中心对称图形?是中心对称图形的,找出它的对称中心.
解:方块5、黑桃Q和花子8的牌面是中心对称图形.
对称中心分别为牌面的两对角线交点.
练习:
如图,已知△ABC与△A′B′C′中心对称,
求出它们的对称中心O.
A
B
C
A′
B′
C′
巩固练习
解法一:根据观察,B、B′应是对应点,连结
BB′,用刻度尺找出BB′的中点O,
则点O即为所求(如图)
A
B
C
A′
B′
C ′
O
O
解法二:根据观察,B、B′及C、C ′应分别是两
组对应点,连结BB′ 、CC′ ,它们相
交于点O,则点O即为所求(如图).
A
B
C
A′
B′
C′
探索活动四
观察下列图案说一说它们有什么共同特征?
在日常生活中,你还见到过具有这种特征的图案吗?试举例说明.
把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形互相重合,那么这个图形叫做中心对称图形.这个点就是它的对称中心.
中心对称与轴对称有什么区别 又有什么联系
轴对称 中心对称
有一条对称轴——直线 有一个对称中心——点
图形沿对称轴对折(翻折180°)后重合 图形绕对称中心旋转180°后重合
折叠后与另一图形重合 旋转后与另一图形重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
探索活动五
我们知道,轴对称与轴对称图形既有联系又有区别.
1.如图,在△ABC中,O是AC的中点,画△ABC关于点O对称的△A′B′C′.
A
B
C
O
(A′)
B′
(C′)
(O′)
2.线段是中心对称图形吗?如果是,说出它的对称中心.
答:线段是中心对称图形,对称中心既是线段中点.
3.在正方形的4个角上剪去4个相同的小正方形(如图),剩余部分是中心对称图形吗?如果是,画出它的对称中心.
O
答:是中心对称图形,O既是对称中心.
轴对称 中心对称
有一条对称轴——直线 有一个对称中心——点
图形沿对称轴对折(翻折180°)后重合 图形绕对称中心旋转180°后重合
折叠后与另一图形重合 旋转后与另一图形重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
课堂小结
1.一个图形绕着某一点旋转180 °,如果它能够与另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称.这个点叫做对称中心.
2.成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
谢谢聆听
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
