9.3 平行四边形(第2课时) 课件(共36张PPT)
文档属性
| 名称 | 9.3 平行四边形(第2课时) 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 19:57:30 | ||
图片预览





文档简介
9.3 平行四边形
第2课时
第9章 中心对称图形——平行四边形
2020-2021学年度苏科版八年级下册
两组对边都不平行.
一组对边平行,
一组对边不平行.
两组对边分别平行.
四边形.
平行四边形
有两组对边分别平行的四边形叫做平行四边形.
观察图形,说出下列图形边的位置有什么特征?
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征.
2
3
1
4
5
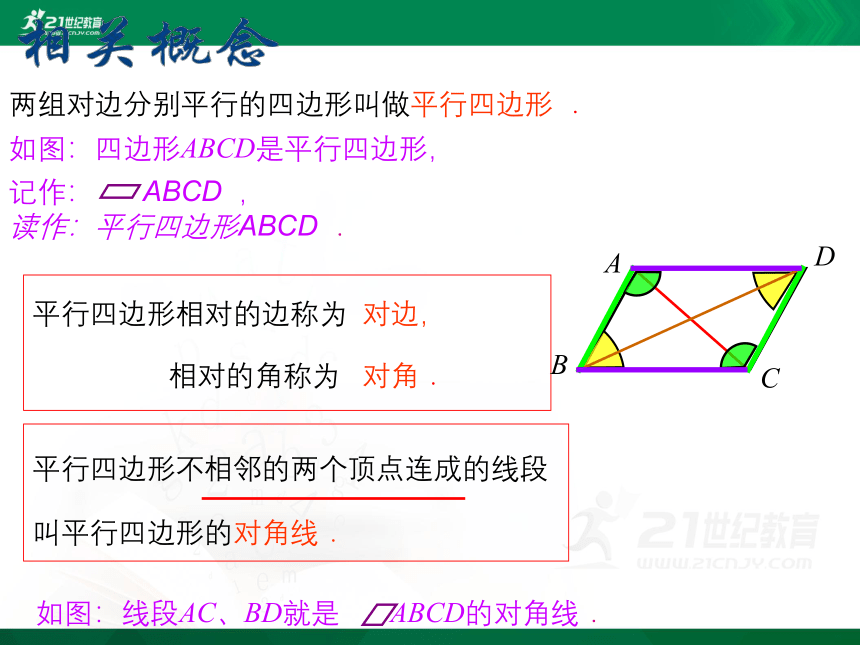
平行四边形相对的边称为 对边,
相对的角称为 对角.
如图:线段AC、BD就是 ABCD的对角线.
A
D
C
B
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
两组对边分别平行的四边形叫做平行四边形 .
如图:四边形ABCD是平行四边形,
记作: ABCD ,
读作:平行四边形ABCD .
●
A
D
O
C
B
D
B
O
C
A
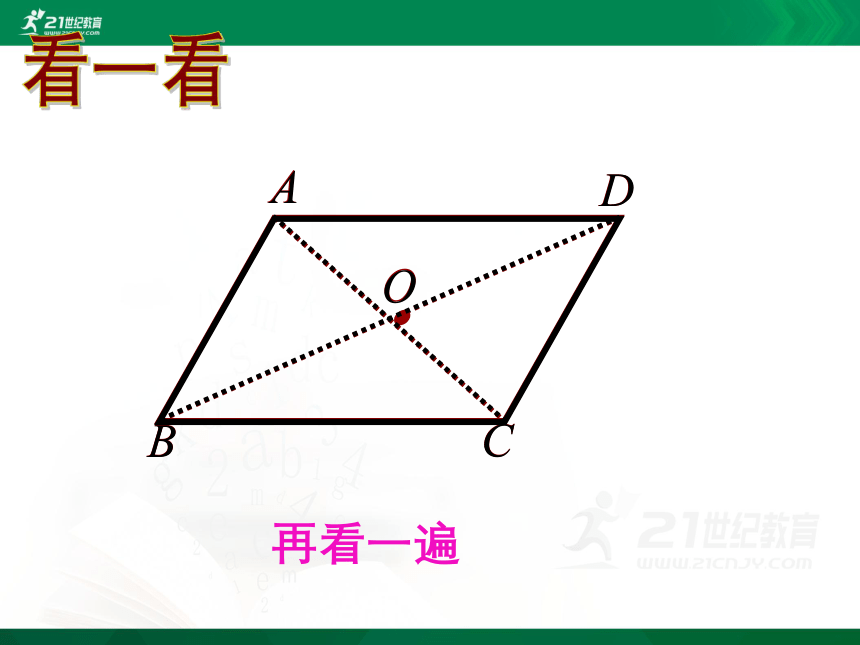
再看一遍
看一看
●
A
D
O
C
B
D
B
O
C
A
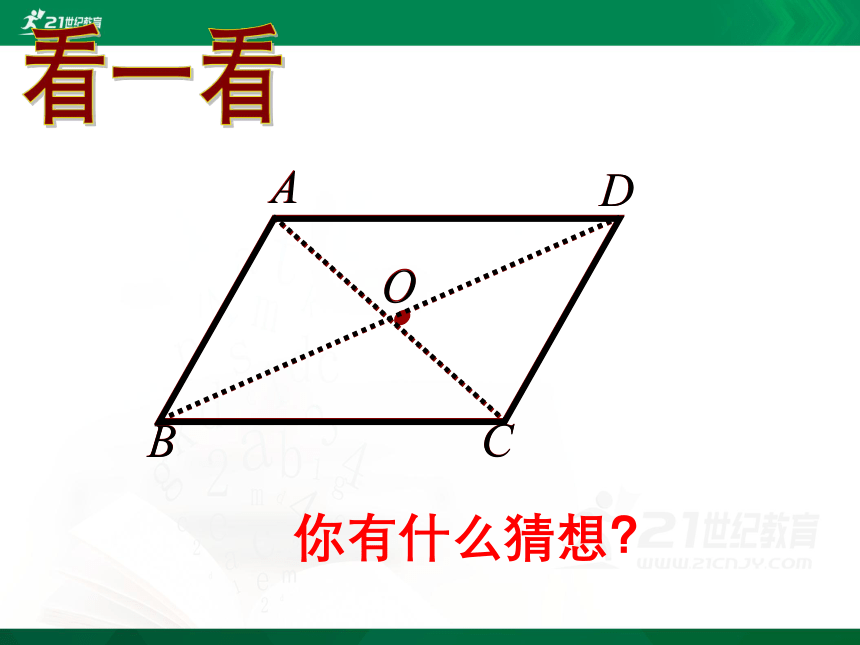
看一看
你有什么猜想?
结论
1. □ABCD绕它的中心O旋转180°后与自身重合,这时我们说□ABCD是 中心对称图形,点O叫对称中心.
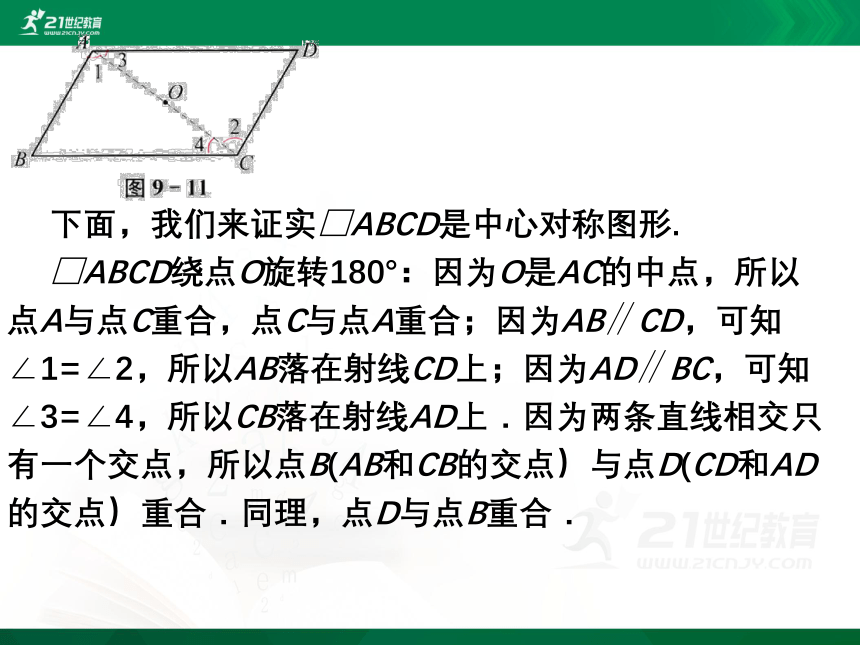
下面,我们来证实□ABCD是中心对称图形.
□ABCD绕点O旋转180°:因为O是AC的中点,所以点A与点C重合,点C与点A重合;因为AB∥CD,可知∠1=∠2,所以AB落在射线CD上;因为AD∥BC,可知∠3=∠4,所以CB落在射线AD上.因为两条直线相交只有一个交点,所以点B(AB和CB的交点)与点D(CD和AD的交点)重合.同理,点D与点B重合.
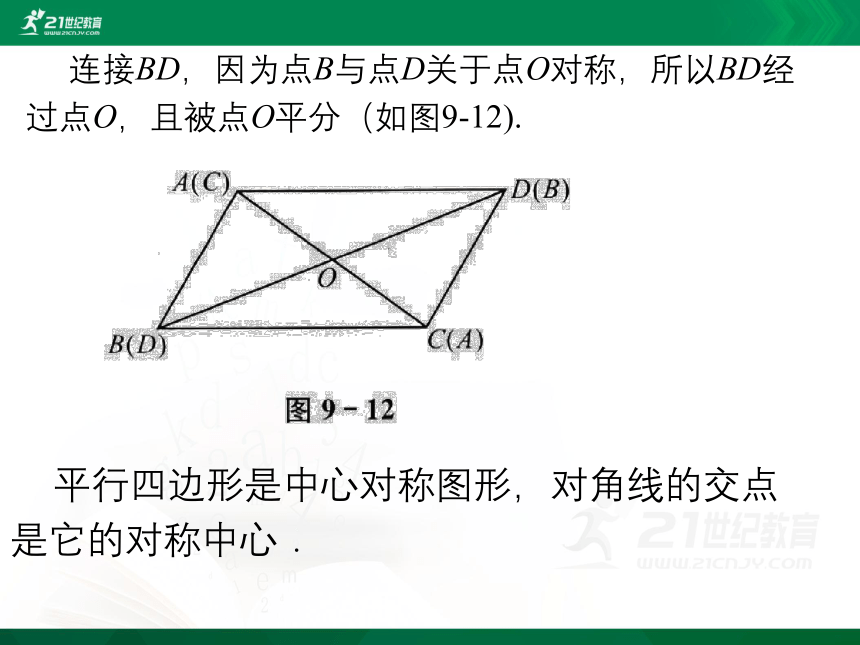
连接BD,因为点B与点D关于点O对称,所以BD经过点O,且被点O平分(如图9-12).
平行四边形是中心对称图形,对角线的交点是它的对称中心.
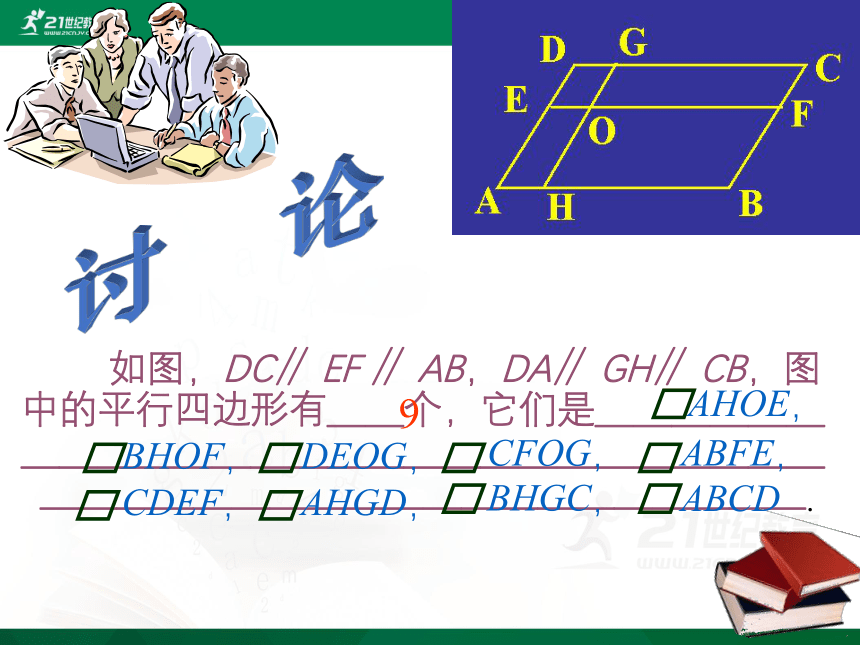
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
讨 论
9
AHOE,
ABCD .
BHGC,
AHGD,
CDEF,
ABFE,
CFOG,
DEOG,
BHOF,
A
B
D
C
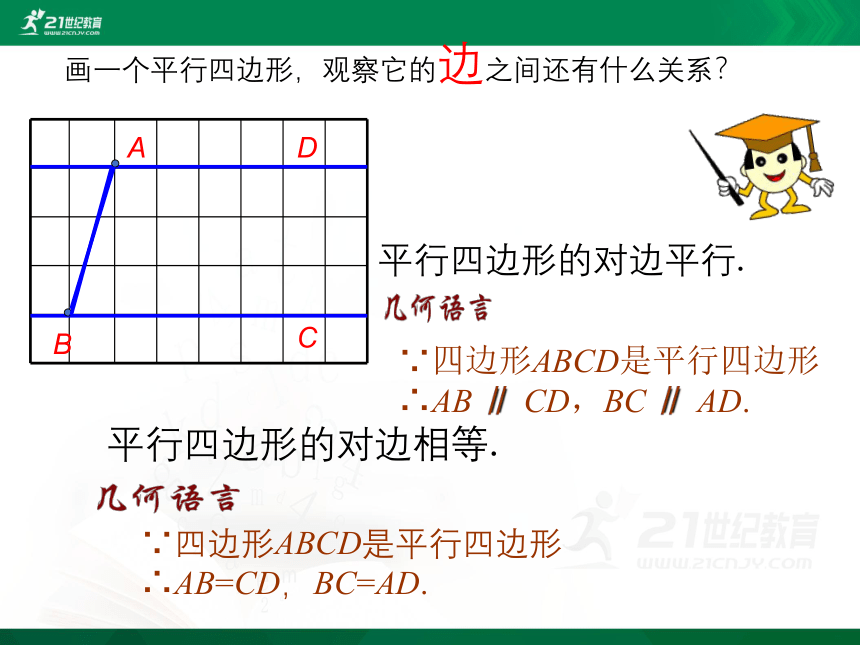
画一个平行四边形,观察它的边之间还有什么关系?
平行四边形的对边平行.
∵四边形ABCD是平行四边形∴AB ∥ CD,BC ∥ AD.
∵四边形ABCD是平行四边形∴AB=CD,BC=AD.
平行四边形的对边相等.
例1 已知:如图9-13,点A、B、C分别在△EFD的各边上,且AB//DE,BC//EF,CA//FD
求证:A、B、C分别是△DEF各边的中点.
证明:∵CA//FD,BC//EF,
∴四边形AFBC是平行四边形(两组对边分别平行的四边形是平行四边形).
∴AF=BC(平行四边形的对边相等).
∵AB//DE,BC//EF,
∴四边形ABCE是平行四边形(两组对边分别平行的四边形是平行四边形)
∴AE=BC(平行四边形的对边相等).
∴AF=AE.
同理BD=BF,CD=CE.
∴A、B、C分别是△DEF各边的中点.
A
D
C
B
4
3
解: ∵BD ⊥AD
∴ ∠ADB=90 °
在Rt △ADB中,AD=3,BD=4
∴AB= = 5(勾股定理)
又∵四边形ABCD为平行四边形(已知)
∴ AD=BC=3
AB=DC=5
∴ ABCD的周长=2(AD+AB)
=2(3+5)
=16
(平行四边形对边相等)
如图,已知 ABCD 中,AD=3,BD⊥AD, 且BD=4, 你能求出平行四边形的周长吗?
学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
A1
A3
A2
A
B
C
如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
A
B
C
D
解:
四边形ABCD是平行四边形,
A
B
C
D
已知: ABCD的周长等于20 cm,AC=7 cm,求△ABC的周长.
解:
∵四边形ABCD是平行四边形(已知)
∴ AB=CD,BC=AD(平行四边形的对边相等)
即AB+BC= C ,
ABCD =10cm,
又∵ AC=7 cm(已知)
∴ C△ ABC=AB+BC+AC=10+7=17(cm).
探究
旋转平行四边形,探究对称性和角的关系.
C
A
B
D
平行四边形是中心对称图形.
平行四边形的对角相等.
∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D.
O
A
B
C
D
解:
∵四边形ABCD是平行四边形
且∠A=52°(已知)
∴ ∠A=∠C=52°(平行四边形的对角相等)
又∵AD∥BC(平行四边形的对边平行)
∴∠A+∠B=180°(两直线平行,同旁内角互补)
∴∠B=∠D= 180 °-∠A= 180?- 52°=128 °
在 ABCD中,已知∠A=52 ° ,求其余三个角的度数.
A
B
C
D
52°
如图: 在 ABCD中,∠A+∠C=200°
则:∠A= ,∠B= .
练习:
A
D
B
C
100 °
80 °
解:
∴∠B= 180 °-∠A= 180?- 100°=80°
又∵AD∥BC(平行四边形的对边平行)
∵四边形ABCD是平行四边形
∴∠A=∠C=100 ° (平行四边形的对角相等)
且∠A+∠C=200°
在 ABCD 中, ∠A与∠B 的度数之比为4:5,∠A= , ∠B= , ∠C= ∠D= .
A
B
C
D
80°
100°
80°
100°
在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC= .
C
4cm
A
B
D
E
9cm
1
2
5cm
9cm
3
平行四边形的对边平行且相等;
B
D
C
A
平行四边形的对角相等.
有两组对边分别平行的四边形是平行四边形.
平行四边形概念:
两组对边分别平行的四边形叫平行四边形.
平行四边形的数学符号:“ ” .
D
C
A
B
O
对边:AB与CD,AD与BC.
对角线:AC=BD
对角:
请找出图中的平行四边形,
说明寻找的依据是什么?
.
.
AB=CD,AD=BC (结论1)
操作:
学生任意画一个平行四边形,根据平行四边形中的相关概念,通过实验操作、猜测,尽可能多地寻找、发现平行四边形中除两组对边分别平行外的其它特性.
D
C
A
B
O
(结论2)
(结论3)
AB=CD,AD=BC
操作:
D
C
A
B
O
(结论2)
(结论1)
(结论3)
AO=CO, BO=DO
(结论4)
(结论6)
归纳:
边:
角:
对角线:
(结论5)
△ABO≌△CDO
D
C
A
B
O
AB=CD,AD=BC
结论1:
推理:
学生利用原有知识,对所总结出来的结论进行说理论证.
利用实物投影仪展示各小组
的证明过程,全班展开讨论、交
流,进行修改、补充,在教师的
引导下逐步完善.
结论2:
AO=CO, BO=DO
结论4:
完善:
性质1、平行四边形的对边相等.
性质2、平行四边形的对角相等.
性质3、平行四边形的对角线互相平分.
推理:
D
C
A
B
O
AB=CD,AD=BC
(结论2)
(结论1)
AO=CO, BO=DO
(结论4)
边:
角:
对角线:
归纳:
操作:
平行四边形的性质:
学生在互相讨论、反驳、纠正中以及在教师的启发、引导下,用简洁的语言描述性质,形成对所得结论的理性认识.
例1 已知:如图9-13,点A、B、C分别在△EFD的各边上,且AB//DE,BC//EF,CA//FD
求证:A、B、C分别是△DEF各边的中点.
证明:∵CA//FD,BC//EF,
∴四边形AFBC是平行四边形(两组对边分别平行的四边形是平行四边形).
∴AF=BC(平行四边形的对边相等).
∵AB//DE,BC//EF,
∴四边形ABCE是平行四边形(两组对边分别平行的四边形是平行四边形)
∴AE=BC(平行四边形的对边相等).
∴AF=AE.
同理BD=BF,CD=CE.
∴A、B、C分别是△DEF各边的中点.
D
C
A
B
O
1、填空题:
(1)如图, ABCD的两条对角线相交于点O,已知OA,OB,AB的长度分别为3cm,4cm,5cm,那么CD =________cm,AC=_________cm,
BD=________cm.
?
(2)如图,已知点C在BD上,△ABC中
,且四边形ACDE是平行四边形,
那么,图中与ED相等的线段有_________;
与 相等的角有 .
A
B
C
D
E
2、在 ABCD中,已知 ,
求四边形各个内角的度数.
3、如图:在笔直的铁轨上夹在两根铁轨之间的枕木是否一样长?
谢谢聆听
第2课时
第9章 中心对称图形——平行四边形
2020-2021学年度苏科版八年级下册
两组对边都不平行.
一组对边平行,
一组对边不平行.
两组对边分别平行.
四边形.
平行四边形
有两组对边分别平行的四边形叫做平行四边形.
观察图形,说出下列图形边的位置有什么特征?
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征.
2
3
1
4
5
平行四边形相对的边称为 对边,
相对的角称为 对角.
如图:线段AC、BD就是 ABCD的对角线.
A
D
C
B
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
两组对边分别平行的四边形叫做平行四边形 .
如图:四边形ABCD是平行四边形,
记作: ABCD ,
读作:平行四边形ABCD .
●
A
D
O
C
B
D
B
O
C
A
再看一遍
看一看
●
A
D
O
C
B
D
B
O
C
A
看一看
你有什么猜想?
结论
1. □ABCD绕它的中心O旋转180°后与自身重合,这时我们说□ABCD是 中心对称图形,点O叫对称中心.
下面,我们来证实□ABCD是中心对称图形.
□ABCD绕点O旋转180°:因为O是AC的中点,所以点A与点C重合,点C与点A重合;因为AB∥CD,可知∠1=∠2,所以AB落在射线CD上;因为AD∥BC,可知∠3=∠4,所以CB落在射线AD上.因为两条直线相交只有一个交点,所以点B(AB和CB的交点)与点D(CD和AD的交点)重合.同理,点D与点B重合.
连接BD,因为点B与点D关于点O对称,所以BD经过点O,且被点O平分(如图9-12).
平行四边形是中心对称图形,对角线的交点是它的对称中心.
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
讨 论
9
AHOE,
ABCD .
BHGC,
AHGD,
CDEF,
ABFE,
CFOG,
DEOG,
BHOF,
A
B
D
C
画一个平行四边形,观察它的边之间还有什么关系?
平行四边形的对边平行.
∵四边形ABCD是平行四边形∴AB ∥ CD,BC ∥ AD.
∵四边形ABCD是平行四边形∴AB=CD,BC=AD.
平行四边形的对边相等.
例1 已知:如图9-13,点A、B、C分别在△EFD的各边上,且AB//DE,BC//EF,CA//FD
求证:A、B、C分别是△DEF各边的中点.
证明:∵CA//FD,BC//EF,
∴四边形AFBC是平行四边形(两组对边分别平行的四边形是平行四边形).
∴AF=BC(平行四边形的对边相等).
∵AB//DE,BC//EF,
∴四边形ABCE是平行四边形(两组对边分别平行的四边形是平行四边形)
∴AE=BC(平行四边形的对边相等).
∴AF=AE.
同理BD=BF,CD=CE.
∴A、B、C分别是△DEF各边的中点.
A
D
C
B
4
3
解: ∵BD ⊥AD
∴ ∠ADB=90 °
在Rt △ADB中,AD=3,BD=4
∴AB= = 5(勾股定理)
又∵四边形ABCD为平行四边形(已知)
∴ AD=BC=3
AB=DC=5
∴ ABCD的周长=2(AD+AB)
=2(3+5)
=16
(平行四边形对边相等)
如图,已知 ABCD 中,AD=3,BD⊥AD, 且BD=4, 你能求出平行四边形的周长吗?
学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
A1
A3
A2
A
B
C
如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
A
B
C
D
解:
四边形ABCD是平行四边形,
A
B
C
D
已知: ABCD的周长等于20 cm,AC=7 cm,求△ABC的周长.
解:
∵四边形ABCD是平行四边形(已知)
∴ AB=CD,BC=AD(平行四边形的对边相等)
即AB+BC= C ,
ABCD =10cm,
又∵ AC=7 cm(已知)
∴ C△ ABC=AB+BC+AC=10+7=17(cm).
探究
旋转平行四边形,探究对称性和角的关系.
C
A
B
D
平行四边形是中心对称图形.
平行四边形的对角相等.
∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D.
O
A
B
C
D
解:
∵四边形ABCD是平行四边形
且∠A=52°(已知)
∴ ∠A=∠C=52°(平行四边形的对角相等)
又∵AD∥BC(平行四边形的对边平行)
∴∠A+∠B=180°(两直线平行,同旁内角互补)
∴∠B=∠D= 180 °-∠A= 180?- 52°=128 °
在 ABCD中,已知∠A=52 ° ,求其余三个角的度数.
A
B
C
D
52°
如图: 在 ABCD中,∠A+∠C=200°
则:∠A= ,∠B= .
练习:
A
D
B
C
100 °
80 °
解:
∴∠B= 180 °-∠A= 180?- 100°=80°
又∵AD∥BC(平行四边形的对边平行)
∵四边形ABCD是平行四边形
∴∠A=∠C=100 ° (平行四边形的对角相等)
且∠A+∠C=200°
在 ABCD 中, ∠A与∠B 的度数之比为4:5,∠A= , ∠B= , ∠C= ∠D= .
A
B
C
D
80°
100°
80°
100°
在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC= .
C
4cm
A
B
D
E
9cm
1
2
5cm
9cm
3
平行四边形的对边平行且相等;
B
D
C
A
平行四边形的对角相等.
有两组对边分别平行的四边形是平行四边形.
平行四边形概念:
两组对边分别平行的四边形叫平行四边形.
平行四边形的数学符号:“ ” .
D
C
A
B
O
对边:AB与CD,AD与BC.
对角线:AC=BD
对角:
请找出图中的平行四边形,
说明寻找的依据是什么?
.
.
AB=CD,AD=BC (结论1)
操作:
学生任意画一个平行四边形,根据平行四边形中的相关概念,通过实验操作、猜测,尽可能多地寻找、发现平行四边形中除两组对边分别平行外的其它特性.
D
C
A
B
O
(结论2)
(结论3)
AB=CD,AD=BC
操作:
D
C
A
B
O
(结论2)
(结论1)
(结论3)
AO=CO, BO=DO
(结论4)
(结论6)
归纳:
边:
角:
对角线:
(结论5)
△ABO≌△CDO
D
C
A
B
O
AB=CD,AD=BC
结论1:
推理:
学生利用原有知识,对所总结出来的结论进行说理论证.
利用实物投影仪展示各小组
的证明过程,全班展开讨论、交
流,进行修改、补充,在教师的
引导下逐步完善.
结论2:
AO=CO, BO=DO
结论4:
完善:
性质1、平行四边形的对边相等.
性质2、平行四边形的对角相等.
性质3、平行四边形的对角线互相平分.
推理:
D
C
A
B
O
AB=CD,AD=BC
(结论2)
(结论1)
AO=CO, BO=DO
(结论4)
边:
角:
对角线:
归纳:
操作:
平行四边形的性质:
学生在互相讨论、反驳、纠正中以及在教师的启发、引导下,用简洁的语言描述性质,形成对所得结论的理性认识.
例1 已知:如图9-13,点A、B、C分别在△EFD的各边上,且AB//DE,BC//EF,CA//FD
求证:A、B、C分别是△DEF各边的中点.
证明:∵CA//FD,BC//EF,
∴四边形AFBC是平行四边形(两组对边分别平行的四边形是平行四边形).
∴AF=BC(平行四边形的对边相等).
∵AB//DE,BC//EF,
∴四边形ABCE是平行四边形(两组对边分别平行的四边形是平行四边形)
∴AE=BC(平行四边形的对边相等).
∴AF=AE.
同理BD=BF,CD=CE.
∴A、B、C分别是△DEF各边的中点.
D
C
A
B
O
1、填空题:
(1)如图, ABCD的两条对角线相交于点O,已知OA,OB,AB的长度分别为3cm,4cm,5cm,那么CD =________cm,AC=_________cm,
BD=________cm.
?
(2)如图,已知点C在BD上,△ABC中
,且四边形ACDE是平行四边形,
那么,图中与ED相等的线段有_________;
与 相等的角有 .
A
B
C
D
E
2、在 ABCD中,已知 ,
求四边形各个内角的度数.
3、如图:在笔直的铁轨上夹在两根铁轨之间的枕木是否一样长?
谢谢聆听
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
