2020—2021学年苏科版七年级数学下册《第7章基本的平面图形(二)》高频易错专项训练(word版附答案)
文档属性
| 名称 | 2020—2021学年苏科版七年级数学下册《第7章基本的平面图形(二)》高频易错专项训练(word版附答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 146.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 00:00:00 | ||
图片预览


文档简介
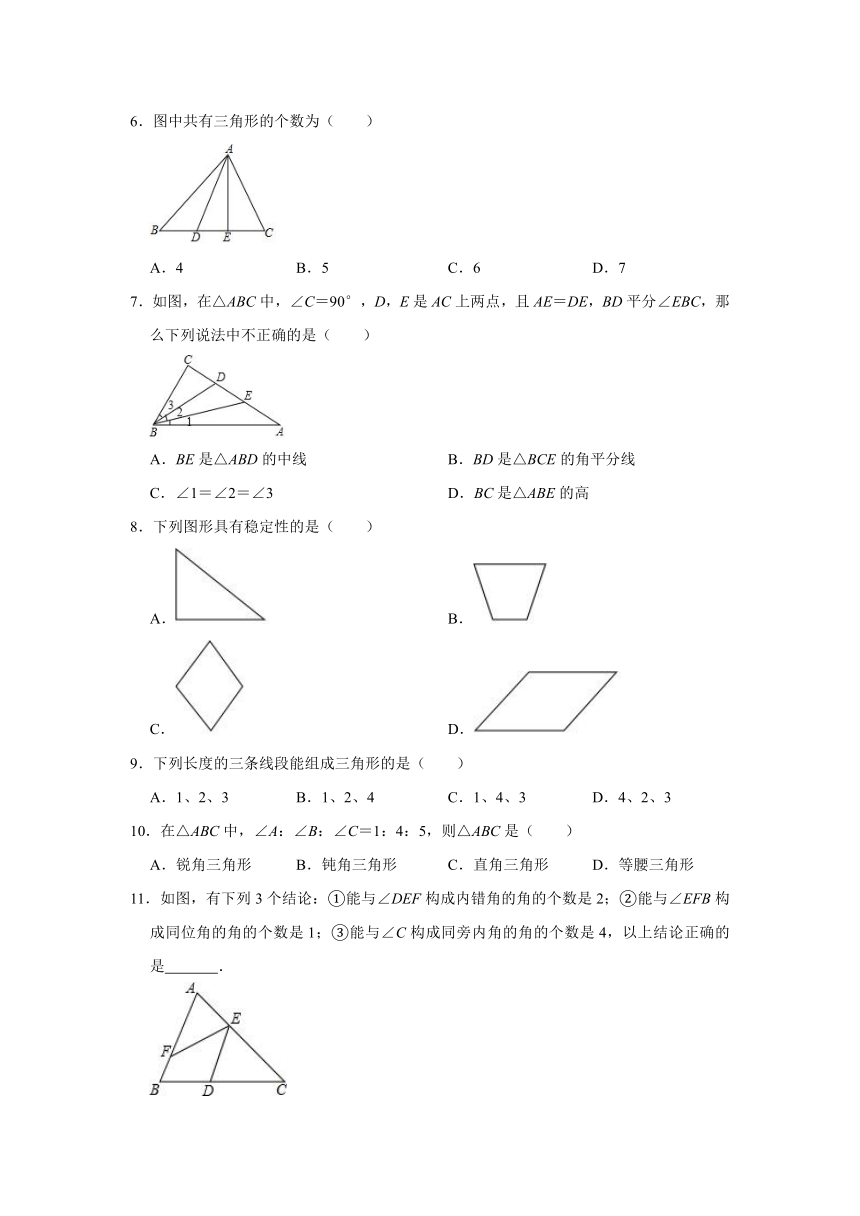
2021年苏科版七年级数学下册《第7章基本的平面图形(二)》高频易错专项训练(附答案)
1.如图的四个图中,∠1与∠2是同位角的有( )
A.②③ B.①②③ C.① D.①②④
2.如图,下列条件中不能判定AB∥CD的是( )
A.∠3=∠4 B.∠1=∠5 C.∠4+∠5=180° D.∠3+∠5=180°
3.如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( )
A.相等 B.互余或互补 C.互补 D.相等或互补
4.下列说法:
①相等的角是对顶角;
②平面内,过一点有且只有一条直线与已知直线垂直;
③平行于同一条直线的两条直线互相平行;
④同角或等角的余角相等,
其中正确的说法有( )
A.4 个 B.3 个 C.2 个 D.1 个
5.如图,AB∥EF,C点在EF上,∠EAC=∠ECA,BC平分∠DCF,且AC⊥BC.下列结论:①AC平分∠DCE;②AE∥CD;③∠1+∠B=90°;④∠BDC=2∠1.
其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
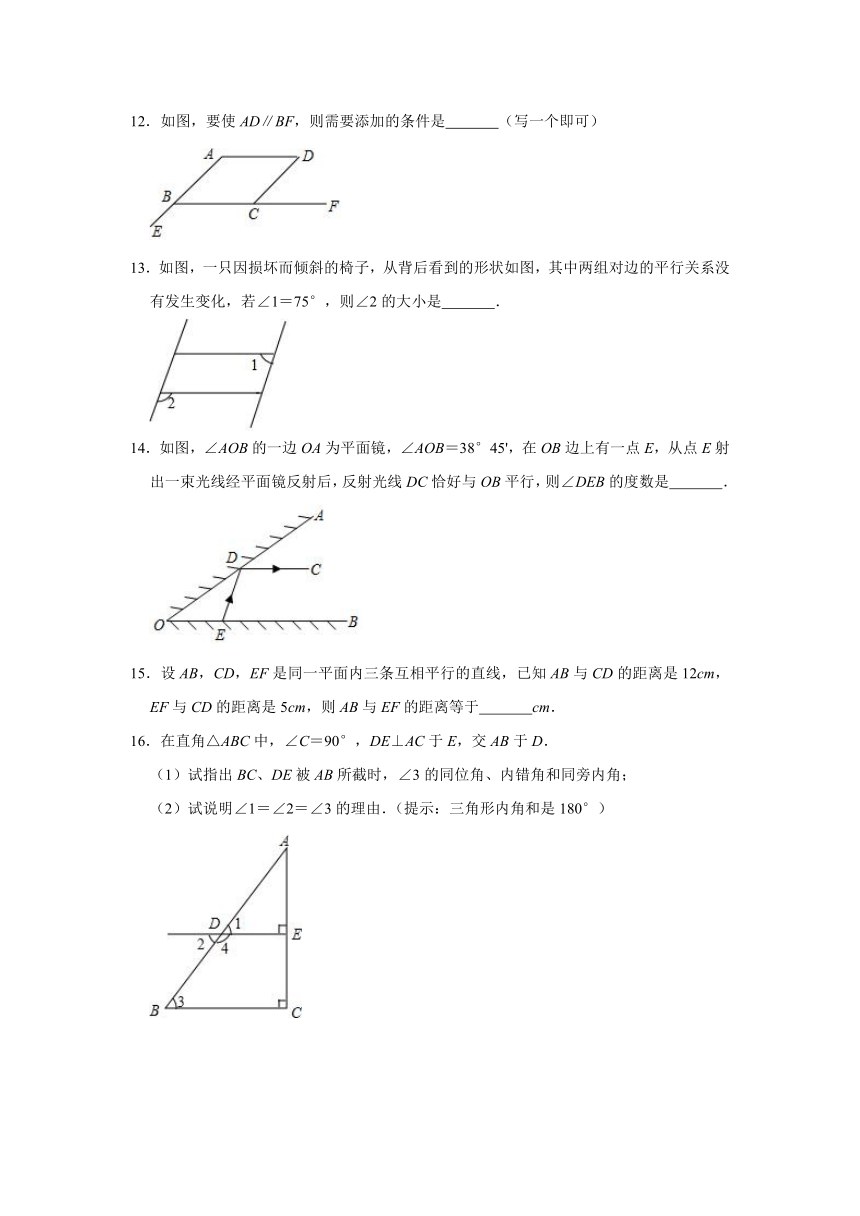
6.图中共有三角形的个数为( )
A.4 B.5 C.6 D.7
7.如图,在△ABC中,∠C=90°,D,E是AC上两点,且AE=DE,BD平分∠EBC,那么下列说法中不正确的是( )
A.BE是△ABD的中线 B.BD是△BCE的角平分线
C.∠1=∠2=∠3 D.BC是△ABE的高
8.下列图形具有稳定性的是( )
A. B.
C. D.
9.下列长度的三条线段能组成三角形的是( )
A.1、2、3 B.1、2、4 C.1、4、3 D.4、2、3
10.在△ABC中,∠A:∠B:∠C=1:4:5,则△ABC是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
11.如图,有下列3个结论:①能与∠DEF构成内错角的角的个数是2;②能与∠EFB构成同位角的角的个数是1;③能与∠C构成同旁内角的角的个数是4,以上结论正确的是 .
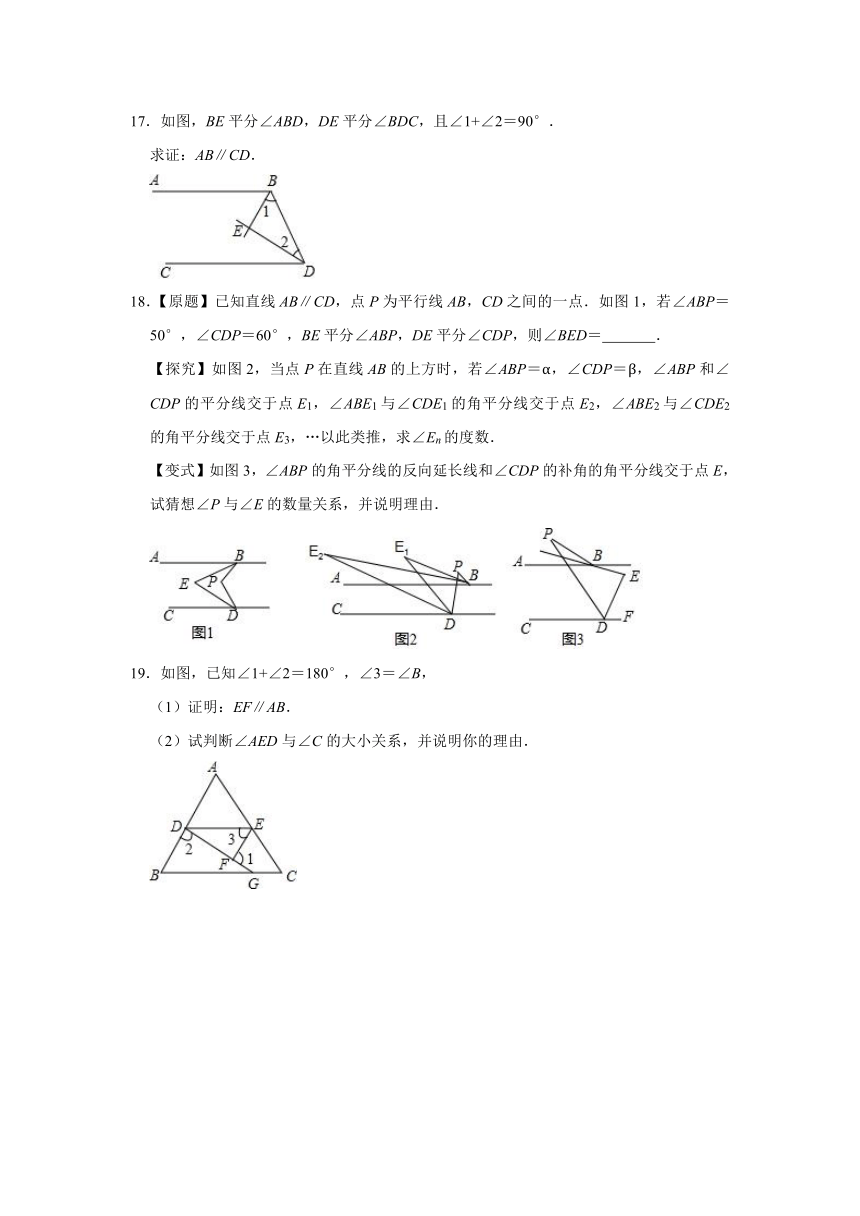
12.如图,要使AD∥BF,则需要添加的条件是 (写一个即可)
13.如图,一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=75°,则∠2的大小是 .
14.如图,∠AOB的一边OA为平面镜,∠AOB=38°45',在OB边上有一点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好与OB平行,则∠DEB的度数是 .
15.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于 cm.
16.在直角△ABC中,∠C=90°,DE⊥AC于E,交AB于D.
(1)试指出BC、DE被AB所截时,∠3的同位角、内错角和同旁内角;
(2)试说明∠1=∠2=∠3的理由.(提示:三角形内角和是180°)
17.如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°.
求证:AB∥CD.
18.【原题】已知直线AB∥CD,点P为平行线AB,CD之间的一点.如图1,若∠ABP=50°,∠CDP=60°,BE平分∠ABP,DE平分∠CDP,则∠BED= .
【探究】如图2,当点P在直线AB的上方时,若∠ABP=α,∠CDP=β,∠ABP和∠CDP的平分线交于点E1,∠ABE1与∠CDE1的角平分线交于点E2,∠ABE2与∠CDE2的角平分线交于点E3,…以此类推,求∠En的度数.
【变式】如图3,∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E,试猜想∠P与∠E的数量关系,并说明理由.
19.如图,已知∠1+∠2=180°,∠3=∠B,
(1)证明:EF∥AB.
(2)试判断∠AED与∠C的大小关系,并说明你的理由.
参考答案
1.解:①∠1和∠2是同位角;
②∠1和∠2是同位角;
③∠1的两边所在的直线没有任何一条和∠2的两边所在的直线公共,∠1和∠2不是同位角;
④∠1和∠2是同位角.
∴∠1与∠2是同位角的有①②④.
故选:D.
2.解:A、∵∠3=∠4,
∴AB∥CD,故本选项能判定AB∥CD;
B、∵∠1=∠5,
∴AB∥CD,故本选项能判定AB∥CD;
C、根据∠4+∠5=180°不能推出AB∥CD,
故本选项不能判定AB∥CD;
D、∵∠3+∠5=180°,
∴AB∥CD,故本选项能判定AB∥CD;
故选:C.
3.解:如图知∠A和∠B的关系是相等或互补.
故选:D.
4.解:①相等的角不一定是对顶角,原说法错误;
②平面内,过一点有且只有一条直线与已知直线垂直,原说法正确;
③平行于同一条直线的两条直线互相平行,原说法正确;
④同角或等角的余角相等,原说法正确.
正确的说法有3个,
故选:B.
5.解:∵AB∥EF,
∴∠ECA=∠BAC,∠BCF=∠B,
∵AC⊥BC,
∴∠BAC=90°,
∴∠1+∠BCD=90°,∠ECA+∠BCF=90°,
∵BC平分∠DCF,
∴∠BCD=∠BCF,
∴∠1=∠ECA,
∴AC平分∠DCE,①正确;
∵∠EAC=∠ECA,
∴∠EAC=∠1,
∴AE∥CD,②正确;
∵∠BCF=∠B,∠BCD=∠BCF,
∴∠B=∠BCD,
∴∠1+∠B=90°,③正确;
∵∠1=∠ECA=∠BAC,∠BDC=∠BAC+∠1,
∴∠BDC=2∠1,④正确;
故选:D.
6.解:图中有:△ABC,△ABD,△ABE,△ACD,△ACE,△ADE,
共6个.
故选:C.
7.解:A、∵AE=DE,∴BE是△ABD的中线,正确;
B、∵BD平分∠EBC,∴BD是△EBC的角平分线,正确;
C、∵BD是△EBC的角平分线,
∴∠EBD=∠CBD,
∵BE是中线,
∴∠EBD≠∠ABE,
∴∠1=∠2=∠3不正确,符合题意;
D、∵∠C=90°,∴BC是△ABE的高,正确.
故选:C.
8.解:∵三角形具有稳定性,
∴A选项符合题意而B,C,D选项不合题意.
故选:A.
9.解:由1、2、3,可得1+2=3,故不能组成三角形;
由1、2、4,可得1+2<4,故不能组成三角形;
由1、3、4,可得1+3=4,故不能组成三角形;
由2、3、4,可得2+3>4,故能组成三角形;
故选:D.
10.解:设∠A=x,∠B=4x,∠C=5x,
∵∠A+∠B+∠C=180°,
∴x+4x+5x=180°,
解得:x=18°,
∴∠C=90°,
∴△ABC是直角三角形.
故选:C.
11.解:①能与∠DEF构成内错角的角的个数有2个,即∠EFA和∠EDC,故正确;
②能与∠EFB构成同位角的角的个数只有1个:即∠FAE,故正确;
③能与∠C构成同旁内角的角的个数有5个:即∠CDE,∠B,∠CED,∠CEF,∠A,故错误;
所以结论正确的是①②.
故答案为:①②.
12.解:当∠A=∠EBC(或∠D=∠DCF或∠A+∠ABC=180°或∠D+∠BCD=180°)时,AD∥BF,
故答案为:∠A=∠EBC(答案不唯一).
13.解:如图,∵AD∥BC,∠1=75°,
∴∠3=∠1=75°,
∵AB∥CD,
∴∠2=180°﹣∠3=180°﹣75°=105°.
故答案为:105°.
14.解:∵CD∥OB,
∴∠ADC=∠AOB,
∵∠EDO=∠ADC,
∴∠EDO=∠AOB=38°45′,
∴∠DEB=∠AOB+∠EDO=38°45′+38°45′=77°30′,
故答案为:77°30′.
15.解:分两种情况:
①当EF在AB,CD之间时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12﹣5=7(cm).
②当AB,CD在EF同侧时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12+5=17(cm).
综上所述,EF与AB的距离为7cm或17cm.
故答案为:7或17.
16.解:(1)当BC,DE被AB所截时,∠3的同位角为∠1;∠3的内错角为∠2;∠3的同旁内角为∠4;
(2)∵∠1+∠A+∠C=180°,∠3+∠A+∠C=180°,
∴∠1=∠3
∵∠1=∠2
∴∠1=∠2=∠3
17.解:∵BE平分∠ABD,DE平分∠BDC(已知),
∴∠ABD=2∠1,∠BDC=2∠2(角平分线定义),
∵∠1+∠2=90°,
∴∠ABD+∠BDC=2(∠1+∠2)=180°,
∴AB∥CD(同旁内角互补,两直线平行).
18.解:(1)如图1,过E作EF∥AB,而AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠FEB,∠CDE=∠FED,
∴∠BED=∠BEF+∠DEF=∠ABE+∠CDE,
又∵∠ABP=50°,∠CDP=60°,BE平分∠ABP,DE平分∠CDP,
∴∠ABE=∠ABP=25°,∠CDE=∠CDP=30°,
∴∠BED=25°+30°=55°,
故答案为:55°;
(2)如图2,∵∠ABP和∠CDP的平分线交于点E1,
∴∠ABE1=∠ABP=α,∠CDE1=∠CDP=,
∵AB∥CD,
∴∠CDF=∠AFE1=,
∴∠E1=∠AFE1﹣∠ABE1=﹣α=(β﹣α),
∵∠ABE1与∠CDE1的角平分线交于点E2,
∴∠ABE2=∠ABE1=α,∠CDE2=∠CDE1=,
∵AB∥CD,
∴∠CDG=∠AGE2=,
∴∠E2=∠AGE2﹣∠ABE2=(β﹣α),
同理可得,∠E3=(β﹣α),
以此类推,∠En的度数为(β﹣α).
(3)∠DEB=90°﹣∠P.理由如下:
如图3,过E作EG∥AB,而AB∥CD,
∴AB∥CD∥EG,
∴∠MBE=∠BEG,∠FDE=∠GED,
∴∠DEB=∠BEG+∠DEG=∠MBE+∠FDE=∠ABQ+∠FDE,
又∵∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E,
∴∠FDE=∠PDF=(180°﹣∠CDP),∠ABQ=∠ABP,
∴∠DEB=∠ABP+(180°﹣∠CDP)=90°﹣(∠CDP﹣∠ABP),
∵AB∥CD,
∴∠CDP=∠AHP,
∴∠DEB=90°﹣(∠CDP﹣∠ABP)=90°﹣(∠AHP﹣∠ABP)=90°﹣∠P.
19.解:(1)∵∠1+∠DFE=180°(平角定义),∠1+∠2=180°(已知),
∴∠2=∠DFE,
∴EF∥AB(内错角相等,两直线平行);
(2)∠AED与∠C相等.
∵EF∥AB,
∴∠3=∠ADE(两直线平行,内错角相等),
∵∠3=∠B(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠C(两直线平行,同位角相等).
1.如图的四个图中,∠1与∠2是同位角的有( )
A.②③ B.①②③ C.① D.①②④
2.如图,下列条件中不能判定AB∥CD的是( )
A.∠3=∠4 B.∠1=∠5 C.∠4+∠5=180° D.∠3+∠5=180°
3.如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( )
A.相等 B.互余或互补 C.互补 D.相等或互补
4.下列说法:
①相等的角是对顶角;
②平面内,过一点有且只有一条直线与已知直线垂直;
③平行于同一条直线的两条直线互相平行;
④同角或等角的余角相等,
其中正确的说法有( )
A.4 个 B.3 个 C.2 个 D.1 个
5.如图,AB∥EF,C点在EF上,∠EAC=∠ECA,BC平分∠DCF,且AC⊥BC.下列结论:①AC平分∠DCE;②AE∥CD;③∠1+∠B=90°;④∠BDC=2∠1.
其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
6.图中共有三角形的个数为( )
A.4 B.5 C.6 D.7
7.如图,在△ABC中,∠C=90°,D,E是AC上两点,且AE=DE,BD平分∠EBC,那么下列说法中不正确的是( )
A.BE是△ABD的中线 B.BD是△BCE的角平分线
C.∠1=∠2=∠3 D.BC是△ABE的高
8.下列图形具有稳定性的是( )
A. B.
C. D.
9.下列长度的三条线段能组成三角形的是( )
A.1、2、3 B.1、2、4 C.1、4、3 D.4、2、3
10.在△ABC中,∠A:∠B:∠C=1:4:5,则△ABC是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
11.如图,有下列3个结论:①能与∠DEF构成内错角的角的个数是2;②能与∠EFB构成同位角的角的个数是1;③能与∠C构成同旁内角的角的个数是4,以上结论正确的是 .
12.如图,要使AD∥BF,则需要添加的条件是 (写一个即可)
13.如图,一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=75°,则∠2的大小是 .
14.如图,∠AOB的一边OA为平面镜,∠AOB=38°45',在OB边上有一点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好与OB平行,则∠DEB的度数是 .
15.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于 cm.
16.在直角△ABC中,∠C=90°,DE⊥AC于E,交AB于D.
(1)试指出BC、DE被AB所截时,∠3的同位角、内错角和同旁内角;
(2)试说明∠1=∠2=∠3的理由.(提示:三角形内角和是180°)
17.如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°.
求证:AB∥CD.
18.【原题】已知直线AB∥CD,点P为平行线AB,CD之间的一点.如图1,若∠ABP=50°,∠CDP=60°,BE平分∠ABP,DE平分∠CDP,则∠BED= .
【探究】如图2,当点P在直线AB的上方时,若∠ABP=α,∠CDP=β,∠ABP和∠CDP的平分线交于点E1,∠ABE1与∠CDE1的角平分线交于点E2,∠ABE2与∠CDE2的角平分线交于点E3,…以此类推,求∠En的度数.
【变式】如图3,∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E,试猜想∠P与∠E的数量关系,并说明理由.
19.如图,已知∠1+∠2=180°,∠3=∠B,
(1)证明:EF∥AB.
(2)试判断∠AED与∠C的大小关系,并说明你的理由.
参考答案
1.解:①∠1和∠2是同位角;
②∠1和∠2是同位角;
③∠1的两边所在的直线没有任何一条和∠2的两边所在的直线公共,∠1和∠2不是同位角;
④∠1和∠2是同位角.
∴∠1与∠2是同位角的有①②④.
故选:D.
2.解:A、∵∠3=∠4,
∴AB∥CD,故本选项能判定AB∥CD;
B、∵∠1=∠5,
∴AB∥CD,故本选项能判定AB∥CD;
C、根据∠4+∠5=180°不能推出AB∥CD,
故本选项不能判定AB∥CD;
D、∵∠3+∠5=180°,
∴AB∥CD,故本选项能判定AB∥CD;
故选:C.
3.解:如图知∠A和∠B的关系是相等或互补.
故选:D.
4.解:①相等的角不一定是对顶角,原说法错误;
②平面内,过一点有且只有一条直线与已知直线垂直,原说法正确;
③平行于同一条直线的两条直线互相平行,原说法正确;
④同角或等角的余角相等,原说法正确.
正确的说法有3个,
故选:B.
5.解:∵AB∥EF,
∴∠ECA=∠BAC,∠BCF=∠B,
∵AC⊥BC,
∴∠BAC=90°,
∴∠1+∠BCD=90°,∠ECA+∠BCF=90°,
∵BC平分∠DCF,
∴∠BCD=∠BCF,
∴∠1=∠ECA,
∴AC平分∠DCE,①正确;
∵∠EAC=∠ECA,
∴∠EAC=∠1,
∴AE∥CD,②正确;
∵∠BCF=∠B,∠BCD=∠BCF,
∴∠B=∠BCD,
∴∠1+∠B=90°,③正确;
∵∠1=∠ECA=∠BAC,∠BDC=∠BAC+∠1,
∴∠BDC=2∠1,④正确;
故选:D.
6.解:图中有:△ABC,△ABD,△ABE,△ACD,△ACE,△ADE,
共6个.
故选:C.
7.解:A、∵AE=DE,∴BE是△ABD的中线,正确;
B、∵BD平分∠EBC,∴BD是△EBC的角平分线,正确;
C、∵BD是△EBC的角平分线,
∴∠EBD=∠CBD,
∵BE是中线,
∴∠EBD≠∠ABE,
∴∠1=∠2=∠3不正确,符合题意;
D、∵∠C=90°,∴BC是△ABE的高,正确.
故选:C.
8.解:∵三角形具有稳定性,
∴A选项符合题意而B,C,D选项不合题意.
故选:A.
9.解:由1、2、3,可得1+2=3,故不能组成三角形;
由1、2、4,可得1+2<4,故不能组成三角形;
由1、3、4,可得1+3=4,故不能组成三角形;
由2、3、4,可得2+3>4,故能组成三角形;
故选:D.
10.解:设∠A=x,∠B=4x,∠C=5x,
∵∠A+∠B+∠C=180°,
∴x+4x+5x=180°,
解得:x=18°,
∴∠C=90°,
∴△ABC是直角三角形.
故选:C.
11.解:①能与∠DEF构成内错角的角的个数有2个,即∠EFA和∠EDC,故正确;
②能与∠EFB构成同位角的角的个数只有1个:即∠FAE,故正确;
③能与∠C构成同旁内角的角的个数有5个:即∠CDE,∠B,∠CED,∠CEF,∠A,故错误;
所以结论正确的是①②.
故答案为:①②.
12.解:当∠A=∠EBC(或∠D=∠DCF或∠A+∠ABC=180°或∠D+∠BCD=180°)时,AD∥BF,
故答案为:∠A=∠EBC(答案不唯一).
13.解:如图,∵AD∥BC,∠1=75°,
∴∠3=∠1=75°,
∵AB∥CD,
∴∠2=180°﹣∠3=180°﹣75°=105°.
故答案为:105°.
14.解:∵CD∥OB,
∴∠ADC=∠AOB,
∵∠EDO=∠ADC,
∴∠EDO=∠AOB=38°45′,
∴∠DEB=∠AOB+∠EDO=38°45′+38°45′=77°30′,
故答案为:77°30′.
15.解:分两种情况:
①当EF在AB,CD之间时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12﹣5=7(cm).
②当AB,CD在EF同侧时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12+5=17(cm).
综上所述,EF与AB的距离为7cm或17cm.
故答案为:7或17.
16.解:(1)当BC,DE被AB所截时,∠3的同位角为∠1;∠3的内错角为∠2;∠3的同旁内角为∠4;
(2)∵∠1+∠A+∠C=180°,∠3+∠A+∠C=180°,
∴∠1=∠3
∵∠1=∠2
∴∠1=∠2=∠3
17.解:∵BE平分∠ABD,DE平分∠BDC(已知),
∴∠ABD=2∠1,∠BDC=2∠2(角平分线定义),
∵∠1+∠2=90°,
∴∠ABD+∠BDC=2(∠1+∠2)=180°,
∴AB∥CD(同旁内角互补,两直线平行).
18.解:(1)如图1,过E作EF∥AB,而AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠FEB,∠CDE=∠FED,
∴∠BED=∠BEF+∠DEF=∠ABE+∠CDE,
又∵∠ABP=50°,∠CDP=60°,BE平分∠ABP,DE平分∠CDP,
∴∠ABE=∠ABP=25°,∠CDE=∠CDP=30°,
∴∠BED=25°+30°=55°,
故答案为:55°;
(2)如图2,∵∠ABP和∠CDP的平分线交于点E1,
∴∠ABE1=∠ABP=α,∠CDE1=∠CDP=,
∵AB∥CD,
∴∠CDF=∠AFE1=,
∴∠E1=∠AFE1﹣∠ABE1=﹣α=(β﹣α),
∵∠ABE1与∠CDE1的角平分线交于点E2,
∴∠ABE2=∠ABE1=α,∠CDE2=∠CDE1=,
∵AB∥CD,
∴∠CDG=∠AGE2=,
∴∠E2=∠AGE2﹣∠ABE2=(β﹣α),
同理可得,∠E3=(β﹣α),
以此类推,∠En的度数为(β﹣α).
(3)∠DEB=90°﹣∠P.理由如下:
如图3,过E作EG∥AB,而AB∥CD,
∴AB∥CD∥EG,
∴∠MBE=∠BEG,∠FDE=∠GED,
∴∠DEB=∠BEG+∠DEG=∠MBE+∠FDE=∠ABQ+∠FDE,
又∵∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E,
∴∠FDE=∠PDF=(180°﹣∠CDP),∠ABQ=∠ABP,
∴∠DEB=∠ABP+(180°﹣∠CDP)=90°﹣(∠CDP﹣∠ABP),
∵AB∥CD,
∴∠CDP=∠AHP,
∴∠DEB=90°﹣(∠CDP﹣∠ABP)=90°﹣(∠AHP﹣∠ABP)=90°﹣∠P.
19.解:(1)∵∠1+∠DFE=180°(平角定义),∠1+∠2=180°(已知),
∴∠2=∠DFE,
∴EF∥AB(内错角相等,两直线平行);
(2)∠AED与∠C相等.
∵EF∥AB,
∴∠3=∠ADE(两直线平行,内错角相等),
∵∠3=∠B(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠C(两直线平行,同位角相等).
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
