2020-2021学年七年级数学苏科版下册 第7章平面图形的认识(二) 单元综合同步训练(word版附解析)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册 第7章平面图形的认识(二) 单元综合同步训练(word版附解析) |  | |
| 格式 | doc | ||
| 文件大小 | 123.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 20:32:30 | ||
图片预览


文档简介
2021年苏科版七年级数学下册《第7章基本的平面图形(二)》单元综合同步训练(附答案)
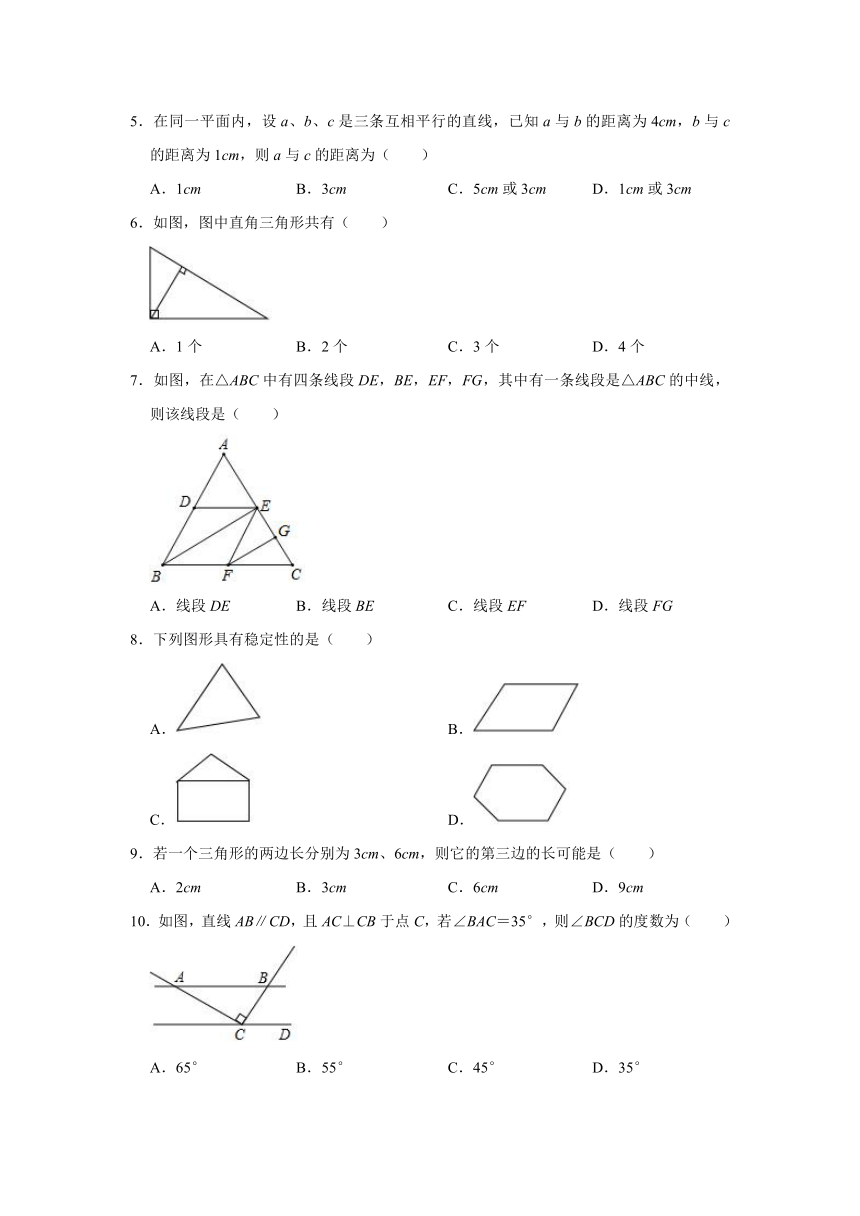
1.如图,直线a,b被直线c所截,则∠1与∠2的位置关系是( )
A.同位角 B.内错角 C.同旁内角 D.邻补角
2.如图,直线a,b被直线c,d所截.下列条件能判定a∥b的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠4=∠5 D.∠1=∠2
3.如图,直线l1∥l2,点A在直线l1上,以点A为圆心,适当长为半径画弧,分别交直线l1,l2于B,C两点,连接AC,BC,若∠ABC=54°,则∠1的度数为( )
A.36° B.54° C.72° D.73°
4.如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b.理由是( )
A.连结直线外一点与直线上各点的所有线段中,垂线段最短
B.在同一平面内,垂直于同一条直线的两条直线互相平行
C.在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线
D.经过直线外一点,有且只有一条直线与这条直线平行
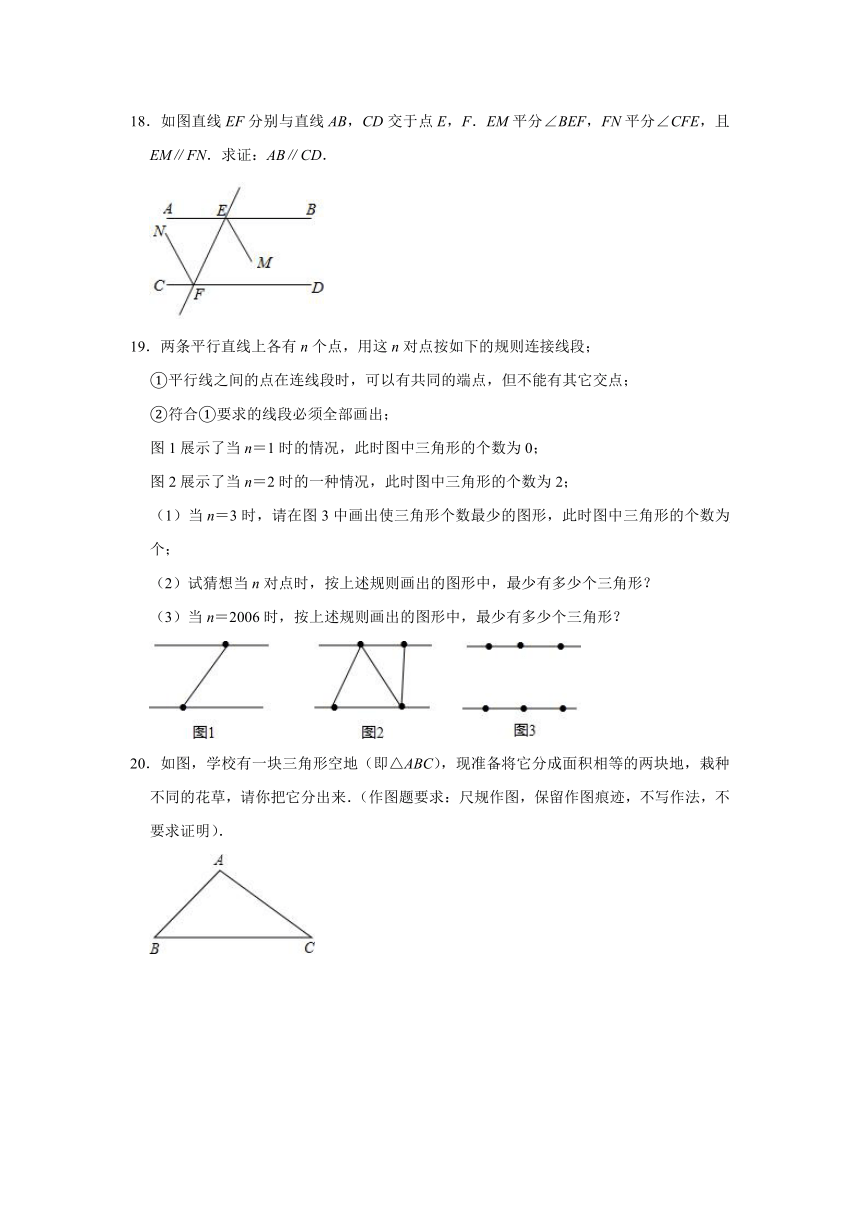
5.在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c的距离为1cm,则a与c的距离为( )
A.1cm B.3cm C.5cm或3cm D.1cm或3cm
6.如图,图中直角三角形共有( )
A.1个 B.2个 C.3个 D.4个
7.如图,在△ABC中有四条线段DE,BE,EF,FG,其中有一条线段是△ABC的中线,则该线段是( )
A.线段DE B.线段BE C.线段EF D.线段FG
8.下列图形具有稳定性的是( )
A. B.
C. D.
9.若一个三角形的两边长分别为3cm、6cm,则它的第三边的长可能是( )
A.2cm B.3cm C.6cm D.9cm
10.如图,直线AB∥CD,且AC⊥CB于点C,若∠BAC=35°,则∠BCD的度数为( )
A.65° B.55° C.45° D.35°
11.如图,请填写一个条件,使结论成立:∵ ,∴a∥b.
12.已知直线a∥b,用一块含30°角的直角三角板按图中所示的方式放置,若∠1=25°,则∠2= .
13.如图,若∠1+∠2=180°,∠3=110°,则∠4= .
14.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于 cm.
15.三角形按边的相等关系分类如下:三角形( )内可填入的是 .
16.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
17.光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面AB与水杯下沿CD平行,光线EF从水中射向空气时发生折射,光线变成FH,点G在射线EF上,已知∠HFB=20°,∠FED=45°,求∠GFH的度数.
18.如图直线EF分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,且EM∥FN.求证:AB∥CD.
19.两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为 个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?
20.如图,学校有一块三角形空地(即△ABC),现准备将它分成面积相等的两块地,栽种不同的花草,请你把它分出来.(作图题要求:尺规作图,保留作图痕迹,不写作法,不要求证明).
参考答案
1.解:如图所示,∠1和∠2两个角都在被截直线b和a同侧,并且在第三条直线c(截线)的同旁,故∠1和∠2是直线b、a被c所截而成的同位角.
故选:A.
2.解:A、当∠1=∠3时,c∥d,故此选项不合题意;
B、当∠2+∠4=180°时,c∥d,故此选项不合题意;
C、当∠4=∠5时,c∥d,故此选项不合题意;
D、当∠1=∠2时,a∥b,故此选项符合题意;
故选:D.
3.解:∵l1∥l2,∠ABC=54°,
∴∠2=∠ABC=54°,
∵以点A为圆心,适当长为半径画弧,分别交直线l1、l2于B、C两点,
∴AC=AB,
∴∠ACB=∠ABC=54°,
∵∠1+∠ACB+∠2=180°,
∴∠1=72°.
故选:C.
4.解:由题意a⊥AB,b⊥AB,
∴a∥b(垂直于同一条直线的两条直线平行),
故选:B.
5.解:当直线c在a、b之间时,
∵a、b、c是三条平行直线,
而a与b的距离为4cm,b与c的距离为1cm,
∴a与c的距离=4﹣1=3(cm);
当直线c不在a、b之间时,
∵a、b、c是三条平行直线,
而a与b的距离为4cm,b与c的距离为1cm,
∴a与c的距离=4+1=5(cm),
综上所述,a与c的距离为5cm或3cm.
故选:C.
6.解:如图,图中直角三角形有Rt△ABD、Rt△BDC、Rt△ABC,共有3个,
故选:C.
7.解:根据三角形中线的定义知线段BE是△ABC的中线,
故选:B.
8.解:三角形具有稳定性.
故选:A.
9.解:设第三边长为xcm,根据三角形的三边关系可得:
6﹣3<x<6+3,
解得:3<x<9,
故选:C.
10.解:∵AC⊥CB,
∴∠ACB=90°,
∴∠ABC=180°﹣90°﹣∠BAC=90°﹣35°=55°,
∵直线AB∥CD,
∴∠ABC=∠BCD=55°,
故选:B.
11.解:∵∠1=∠4或∠2=∠4或∠3+∠4=180°,
∴a∥b.
故答案为:∠1=∠4或∠2=∠4或∠3+∠4=180°.
12.解:过点B作EF∥a.
∵a∥b,
∴EF∥a∥b.
∴∠1=∠ABF,∠2=∠FBC.
∵△ABC是含30°角的直角三角形,
∴∠ABC=60°.
∵∠ABF+∠CBF=60°,
∴∠2=60°﹣25=35°.
故答案为:35°.
13.解:如图,∵∠1+∠2=180°,
∴a∥b,
∴∠3=∠4,
又∵∠3=110°,
∴∠4=110°.
故答案为:110°.
14.解:分两种情况:
①当EF在AB,CD之间时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12﹣5=7(cm).
②当AB,CD在EF同侧时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12+5=17(cm).
综上所述,EF与AB的距离为7cm或17cm.
故答案为:7或17.
15.解:三角形按边可分为:,
故答案为:等边三角形.
16.解:OA∥BC,OB∥AC.
∵∠1=50°,∠2=50°,
∴∠1=∠2,
∴OB∥AC,
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°,
∴OA∥BC.
17.解:∵AB∥CD,
∴∠GFB=∠FED=45°.
∵∠HFB=20°,
∴∠GFH=∠GFB﹣∠HFB=45°﹣20°=25°.
18.证明:∵EM∥FN,
∴∠FEM=∠EFN,
又∵EM平分∠BEF,FN平分∠CFE,
∴∠BEF=2∠FEM,∠EFC=2∠EFN,
∴∠FEB=∠EFC,
∴AB∥CD.
19.解:(1)
4个;
(2)当有n对点时,最少可以画2(n﹣1)个三角形;
(3)2×(2006﹣1)=4010个.
答:当n=2006时,最少可以画4010个三角形.
20.解:作图如下:
1.如图,直线a,b被直线c所截,则∠1与∠2的位置关系是( )
A.同位角 B.内错角 C.同旁内角 D.邻补角
2.如图,直线a,b被直线c,d所截.下列条件能判定a∥b的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠4=∠5 D.∠1=∠2
3.如图,直线l1∥l2,点A在直线l1上,以点A为圆心,适当长为半径画弧,分别交直线l1,l2于B,C两点,连接AC,BC,若∠ABC=54°,则∠1的度数为( )
A.36° B.54° C.72° D.73°
4.如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b.理由是( )
A.连结直线外一点与直线上各点的所有线段中,垂线段最短
B.在同一平面内,垂直于同一条直线的两条直线互相平行
C.在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线
D.经过直线外一点,有且只有一条直线与这条直线平行
5.在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c的距离为1cm,则a与c的距离为( )
A.1cm B.3cm C.5cm或3cm D.1cm或3cm
6.如图,图中直角三角形共有( )
A.1个 B.2个 C.3个 D.4个
7.如图,在△ABC中有四条线段DE,BE,EF,FG,其中有一条线段是△ABC的中线,则该线段是( )
A.线段DE B.线段BE C.线段EF D.线段FG
8.下列图形具有稳定性的是( )
A. B.
C. D.
9.若一个三角形的两边长分别为3cm、6cm,则它的第三边的长可能是( )
A.2cm B.3cm C.6cm D.9cm
10.如图,直线AB∥CD,且AC⊥CB于点C,若∠BAC=35°,则∠BCD的度数为( )
A.65° B.55° C.45° D.35°
11.如图,请填写一个条件,使结论成立:∵ ,∴a∥b.
12.已知直线a∥b,用一块含30°角的直角三角板按图中所示的方式放置,若∠1=25°,则∠2= .
13.如图,若∠1+∠2=180°,∠3=110°,则∠4= .
14.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于 cm.
15.三角形按边的相等关系分类如下:三角形( )内可填入的是 .
16.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
17.光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面AB与水杯下沿CD平行,光线EF从水中射向空气时发生折射,光线变成FH,点G在射线EF上,已知∠HFB=20°,∠FED=45°,求∠GFH的度数.
18.如图直线EF分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,且EM∥FN.求证:AB∥CD.
19.两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为 个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?
20.如图,学校有一块三角形空地(即△ABC),现准备将它分成面积相等的两块地,栽种不同的花草,请你把它分出来.(作图题要求:尺规作图,保留作图痕迹,不写作法,不要求证明).
参考答案
1.解:如图所示,∠1和∠2两个角都在被截直线b和a同侧,并且在第三条直线c(截线)的同旁,故∠1和∠2是直线b、a被c所截而成的同位角.
故选:A.
2.解:A、当∠1=∠3时,c∥d,故此选项不合题意;
B、当∠2+∠4=180°时,c∥d,故此选项不合题意;
C、当∠4=∠5时,c∥d,故此选项不合题意;
D、当∠1=∠2时,a∥b,故此选项符合题意;
故选:D.
3.解:∵l1∥l2,∠ABC=54°,
∴∠2=∠ABC=54°,
∵以点A为圆心,适当长为半径画弧,分别交直线l1、l2于B、C两点,
∴AC=AB,
∴∠ACB=∠ABC=54°,
∵∠1+∠ACB+∠2=180°,
∴∠1=72°.
故选:C.
4.解:由题意a⊥AB,b⊥AB,
∴a∥b(垂直于同一条直线的两条直线平行),
故选:B.
5.解:当直线c在a、b之间时,
∵a、b、c是三条平行直线,
而a与b的距离为4cm,b与c的距离为1cm,
∴a与c的距离=4﹣1=3(cm);
当直线c不在a、b之间时,
∵a、b、c是三条平行直线,
而a与b的距离为4cm,b与c的距离为1cm,
∴a与c的距离=4+1=5(cm),
综上所述,a与c的距离为5cm或3cm.
故选:C.
6.解:如图,图中直角三角形有Rt△ABD、Rt△BDC、Rt△ABC,共有3个,
故选:C.
7.解:根据三角形中线的定义知线段BE是△ABC的中线,
故选:B.
8.解:三角形具有稳定性.
故选:A.
9.解:设第三边长为xcm,根据三角形的三边关系可得:
6﹣3<x<6+3,
解得:3<x<9,
故选:C.
10.解:∵AC⊥CB,
∴∠ACB=90°,
∴∠ABC=180°﹣90°﹣∠BAC=90°﹣35°=55°,
∵直线AB∥CD,
∴∠ABC=∠BCD=55°,
故选:B.
11.解:∵∠1=∠4或∠2=∠4或∠3+∠4=180°,
∴a∥b.
故答案为:∠1=∠4或∠2=∠4或∠3+∠4=180°.
12.解:过点B作EF∥a.
∵a∥b,
∴EF∥a∥b.
∴∠1=∠ABF,∠2=∠FBC.
∵△ABC是含30°角的直角三角形,
∴∠ABC=60°.
∵∠ABF+∠CBF=60°,
∴∠2=60°﹣25=35°.
故答案为:35°.
13.解:如图,∵∠1+∠2=180°,
∴a∥b,
∴∠3=∠4,
又∵∠3=110°,
∴∠4=110°.
故答案为:110°.
14.解:分两种情况:
①当EF在AB,CD之间时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12﹣5=7(cm).
②当AB,CD在EF同侧时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12+5=17(cm).
综上所述,EF与AB的距离为7cm或17cm.
故答案为:7或17.
15.解:三角形按边可分为:,
故答案为:等边三角形.
16.解:OA∥BC,OB∥AC.
∵∠1=50°,∠2=50°,
∴∠1=∠2,
∴OB∥AC,
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°,
∴OA∥BC.
17.解:∵AB∥CD,
∴∠GFB=∠FED=45°.
∵∠HFB=20°,
∴∠GFH=∠GFB﹣∠HFB=45°﹣20°=25°.
18.证明:∵EM∥FN,
∴∠FEM=∠EFN,
又∵EM平分∠BEF,FN平分∠CFE,
∴∠BEF=2∠FEM,∠EFC=2∠EFN,
∴∠FEB=∠EFC,
∴AB∥CD.
19.解:(1)
4个;
(2)当有n对点时,最少可以画2(n﹣1)个三角形;
(3)2×(2006﹣1)=4010个.
答:当n=2006时,最少可以画4010个三角形.
20.解:作图如下:
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
