9.4 矩形、菱形、正方形(第1课时) 课件(共38张PPT)
文档属性
| 名称 | 9.4 矩形、菱形、正方形(第1课时) 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 20:06:24 | ||
图片预览





文档简介
9.4 矩形、菱形、正方形
第1课时 矩形
第9章 中心对称图形——平行四边形
2020-2021学年度苏科版八年级下册
两组对边分别平行的四边形是平行四边形
平行四边形的性质:
边
平行四边形的对边平行;
平行四边形的对边相等;
角
平行四边形的对角相等;
平行四边形的邻角互补.
对角线
平行四边形的对角线互相平分;
温故知新
平行四边形的判定:
边
两组对边分别平行的四边形;
两组对边分别相等的四边形;
角
两组对角分别相等的四边形.
对角线
对角线互相平分的四边形;
一组对边平行且相等的四边形;
平行四边形的判定定理:
一个角是
直角
两组对边
分别平行
平行
四边形
矩形
情景创设
我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,也就是这堂课我们就来研究一种特殊的平行四边形——
矩形
四边形
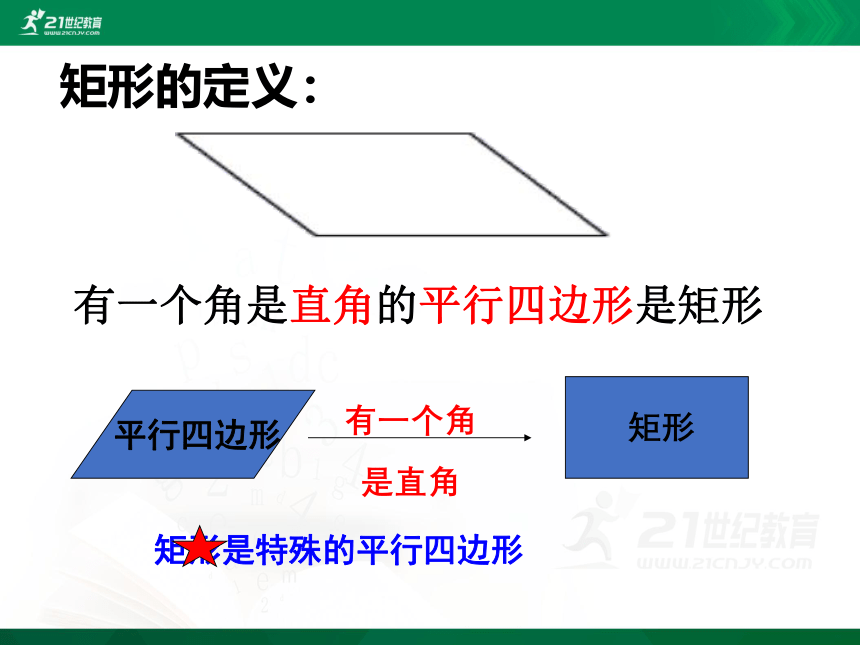
有一个角是直角的平行四边形是矩形
矩形的定义:
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形
对边平行且相等
对角相等
对角线互相平分
矩形的一般性质:
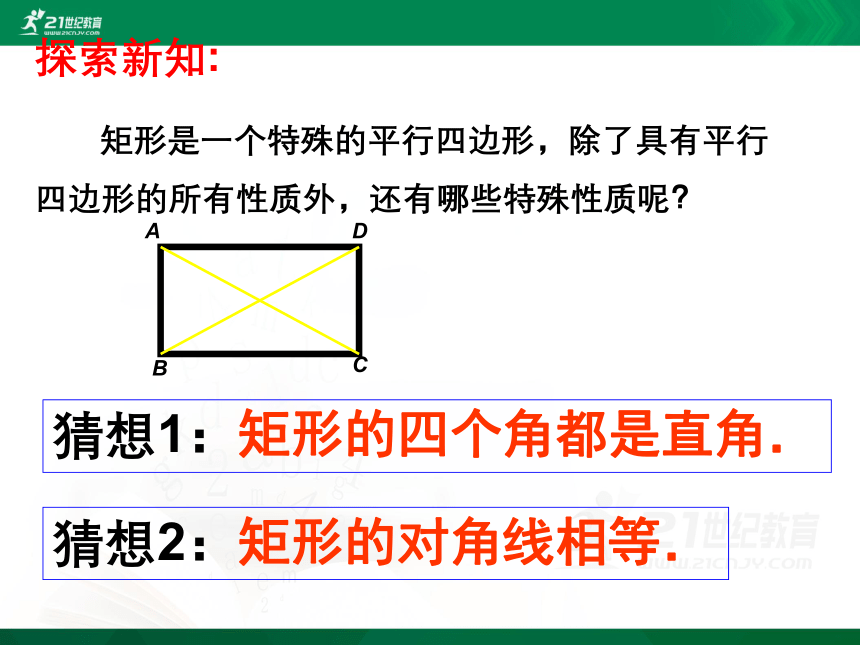
探索新知:
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
A
B
C
D
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明: ∵四边形ABCD是矩形
∴ ∠A=90°
又 矩形ABCD是平行四边形
∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°
∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角.
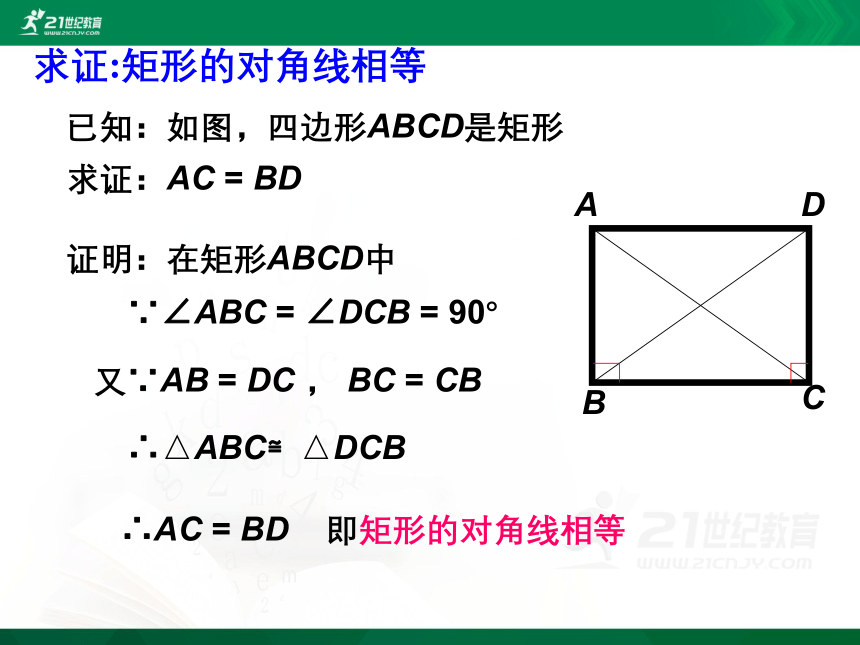
已知:如图,四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD 即矩形的对角线相等
求证:矩形的对角线相等
矩形特殊的性质
矩形的四个角都是直角.
矩形的两条对角线相等.
从角上看:
从对角线上看:
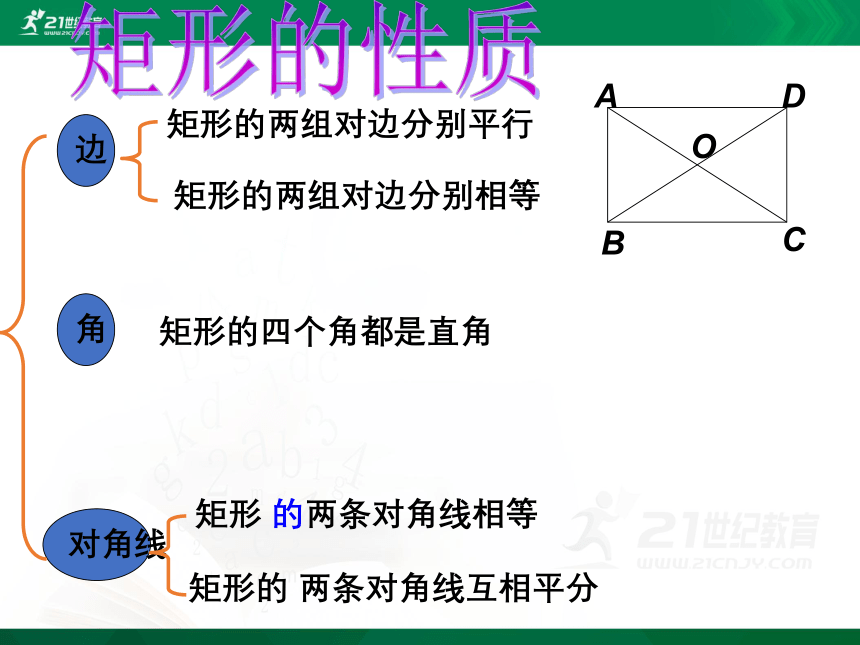
矩形的 两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形的四个角都是直角
矩形 的两条对角线相等
边
对角线
角
A
B
C
D
O
矩形的性质
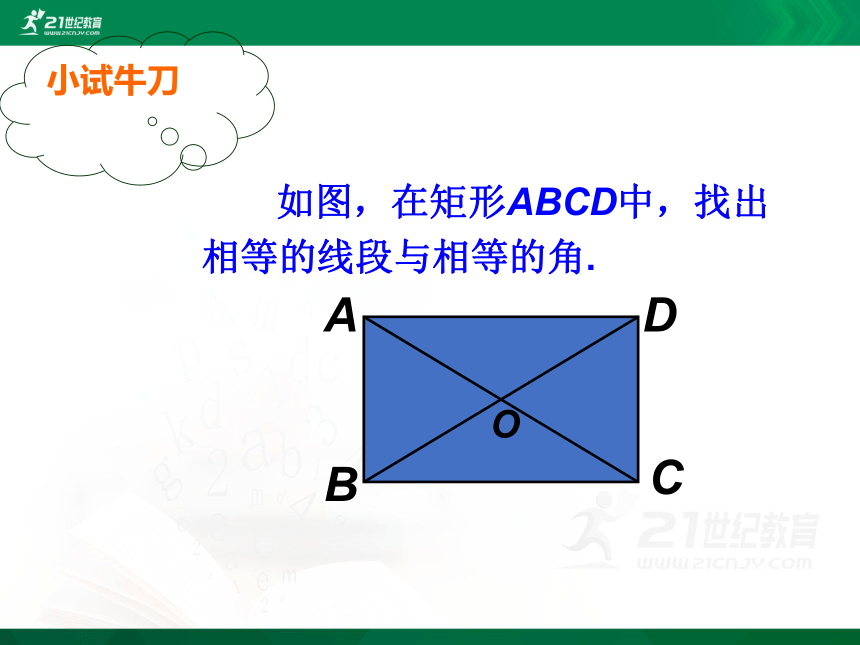
如图,在矩形ABCD中,找出相等的线段与相等的角.
A
D
C
B
O
小试牛刀
O
D
C
B
A
相等的线段:
AB=CD AD=BC AC=BD OA=OC=OB=OD= AC= BD
相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
已知四边形ABCD是矩形
例1 已知:如图9-20,矩形ABCD的两条对角线相交于点O,且AC=2AB.
求证:△AOB是等边三角形.
证明:四边形ABCD是矩形,
∴AC=BD(矩形的对角线相等),
∴
(矩形的对角线互相平分)
∵ 即
∴
△ABC是等边三角形.
矩形具有而一般平行四边形不
具有的性质是 ( )
B.对边相等
A.对角相等
C.对角线相等
D.对角线互相平分
C
营中热身
已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm
O
D
C
B
A
5
10
4
营中寻宝
你知道如何判定一个平行四边形是矩形吗?
矩形的定义:
有一个角是直角的平行四边形是矩形.
你还有其它的判定方法吗?
□ ABCD
∠A=900
四边形ABCD是矩形
情境一:李芳同学由“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?
猜想:有三个角是直角的四边形是矩形 .
你能证明上述结论吗?
解:∵∠AOD=120°,
∴∠AOB=60°,∴△AOB是等边三角形,
∴AO=BO=AB=4 cm,
∴AC=BD=2AO=8 cm.
1.已知:如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=4cm,求矩形对角线的长.
A
B
D
O
C
证明:∵CE∥DB,∴∠E=∠ABO,
又矩形对角线相等且互相平分,
∴AO=BO,∴∠BAO=∠ABO,
∴∠BAO=∠E,
在△AEC中,AC=EC.
2.已知:如图,矩形ABCD的对角线AC、BD相交于点O,CE∥DB,交AB的延长线于点E.
求证:AC=EC.
A
B
D
O
C
E
证明:∵ABCD是矩形,
∴对角线互相平分且相等,∴AO=BO=CO=DO,
又AE=BF=CG=DH,
∴可得EO=FO=GO=HO,∴在EFGH中,对角线互相平分且相等,
故而EFGH是矩形.
1.已知:如图,矩形ABCD的对角线AC、BD相交于O,点E 、 F 、 G 、 H分别在OA 、 OB 、 OC 、 OD上,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
A
H
E
G
F
B
D
C
O
答:可通过测量角度来判定,矩形四个角都是直角.请同学们自由发挥,还有什么其他的判定方式.
2.怎样判断四边形的窗框(如图)是不是矩形?说说你的理由.
1.已知:如图,在菱形ABCD中,对角线AC、BD相交点O,E、F、G、H分别是菱形ABCD各边的中点.
求证:OE=OF=OG=OH.
O
E
F
G
H
B
A
C
D
证明:依次连接各个中点,∵四边形ABCD是菱形
∴AC⊥BD
∵点E、H分别是AD、AB的中点
∴EH∥BD
同理EF∥AC
∴EH⊥EF
即∠FEH=90?
∴四边形EFGH是矩形,
矩形对角线相等且互相平分,
∴OE=OF=OG=OH.
D
B
C
A
H
E
F
G
O
证明:菱形面积即为由对角线所切割的四个三角形的面积之和,
∴SABCD=SAOD+SCOD+SABO+SCBO
又上述四个三角形均为直角三角形,
∴SAOD=1/2·AO·DO,
∴SABCD=1/2(AO+CO)(BO+DO),
∴原命题得证.
D
B
C
A
H
E
F
G
O
矩形的判定方法:
有三个角是直角的四边形是矩形 .
A
B
C
D
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
几何语言:
情境二:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:对角线相等的平行四边形是矩形 .
命题:对角线相等的平行四边形是矩形.
已知:平行四边形ABCD,AC=BD.
求证:四边形ABCD是矩形.
A
B
C
D
证明:
∵ AB=CD, BC=BC, AC=BD
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形
∴四边形ABCD是矩形
∴ ∠ABC=∠DCB
对角线相等的平行四边形是矩形 .
矩形的判定方法:
几何语言:
∵四边形ABCD是平行四边形
AC=BD
∴四边形ABCD是矩形
(对角线相等且互相平分的四边形是矩形.)
A
B
C
D
O
(或OA=OC=OB=OD)
你能归纳矩形的几种判定方法吗?
对角线相等的平行四边形是矩形 .
(对角线相等且互相平分的四边形是矩形.)
有三个角是直角的四边形是矩形 .
方法1:
方法2:
证明:∵∠ACB=90°,D是AB的中点,
∴
∵DC=DA,DF平分∠ADC,
∴DF⊥AC,
即 ∠DFC=90°.
同理∠DEC=90°.
∴四边形DECF是矩形(三个角是直角的四边形是矩形)
例2 已知:如图9-22,在△ABC中,∠ACB=90°,D是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.
求证:四边形DECF是矩形.
下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(10)一组邻边垂直,一组对边平行且相等的四边形是矩形;
(9)对角线相等且互相垂直的四边形是矩形;
(8)一组对角互补的平行四边形是矩形;
(4)有三个角都相等的四边形是矩形;
X
X
X
X
如图,M为平行四边形ABCD边AD的中点,且MB=MC,
求证:四边形ABCD是矩形.
A
B
C
D
M
平行四边形ABCD,E是CD的中点, △ABE是等边三角形.
求证:四边形ABCD是矩形.
D
A
B
C
E
知识总结
性质
判定
边
两组对边分别平行
两组对边分别相等
有一个角是直角的平行四边形是矩形
角
矩形的四个角都是直角
有三个角是直角的四边形是矩形
对角线
矩形的两条对角线相等
对角线相等的平行四边形是矩形
(矩形)
有一个角是直角的平行四边形是矩形.
有三个角是直角的四边形是矩形.
两条对角线相等的平行四边形是矩形.
矩形的四个角都是直角.
矩形的对角线相等.
我的收获
谢谢聆听
第1课时 矩形
第9章 中心对称图形——平行四边形
2020-2021学年度苏科版八年级下册
两组对边分别平行的四边形是平行四边形
平行四边形的性质:
边
平行四边形的对边平行;
平行四边形的对边相等;
角
平行四边形的对角相等;
平行四边形的邻角互补.
对角线
平行四边形的对角线互相平分;
温故知新
平行四边形的判定:
边
两组对边分别平行的四边形;
两组对边分别相等的四边形;
角
两组对角分别相等的四边形.
对角线
对角线互相平分的四边形;
一组对边平行且相等的四边形;
平行四边形的判定定理:
一个角是
直角
两组对边
分别平行
平行
四边形
矩形
情景创设
我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,也就是这堂课我们就来研究一种特殊的平行四边形——
矩形
四边形
有一个角是直角的平行四边形是矩形
矩形的定义:
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形
对边平行且相等
对角相等
对角线互相平分
矩形的一般性质:
探索新知:
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
A
B
C
D
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明: ∵四边形ABCD是矩形
∴ ∠A=90°
又 矩形ABCD是平行四边形
∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°
∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD 即矩形的对角线相等
求证:矩形的对角线相等
矩形特殊的性质
矩形的四个角都是直角.
矩形的两条对角线相等.
从角上看:
从对角线上看:
矩形的 两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形的四个角都是直角
矩形 的两条对角线相等
边
对角线
角
A
B
C
D
O
矩形的性质
如图,在矩形ABCD中,找出相等的线段与相等的角.
A
D
C
B
O
小试牛刀
O
D
C
B
A
相等的线段:
AB=CD AD=BC AC=BD OA=OC=OB=OD= AC= BD
相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
已知四边形ABCD是矩形
例1 已知:如图9-20,矩形ABCD的两条对角线相交于点O,且AC=2AB.
求证:△AOB是等边三角形.
证明:四边形ABCD是矩形,
∴AC=BD(矩形的对角线相等),
∴
(矩形的对角线互相平分)
∵ 即
∴
△ABC是等边三角形.
矩形具有而一般平行四边形不
具有的性质是 ( )
B.对边相等
A.对角相等
C.对角线相等
D.对角线互相平分
C
营中热身
已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm
O
D
C
B
A
5
10
4
营中寻宝
你知道如何判定一个平行四边形是矩形吗?
矩形的定义:
有一个角是直角的平行四边形是矩形.
你还有其它的判定方法吗?
□ ABCD
∠A=900
四边形ABCD是矩形
情境一:李芳同学由“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?
猜想:有三个角是直角的四边形是矩形 .
你能证明上述结论吗?
解:∵∠AOD=120°,
∴∠AOB=60°,∴△AOB是等边三角形,
∴AO=BO=AB=4 cm,
∴AC=BD=2AO=8 cm.
1.已知:如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=4cm,求矩形对角线的长.
A
B
D
O
C
证明:∵CE∥DB,∴∠E=∠ABO,
又矩形对角线相等且互相平分,
∴AO=BO,∴∠BAO=∠ABO,
∴∠BAO=∠E,
在△AEC中,AC=EC.
2.已知:如图,矩形ABCD的对角线AC、BD相交于点O,CE∥DB,交AB的延长线于点E.
求证:AC=EC.
A
B
D
O
C
E
证明:∵ABCD是矩形,
∴对角线互相平分且相等,∴AO=BO=CO=DO,
又AE=BF=CG=DH,
∴可得EO=FO=GO=HO,∴在EFGH中,对角线互相平分且相等,
故而EFGH是矩形.
1.已知:如图,矩形ABCD的对角线AC、BD相交于O,点E 、 F 、 G 、 H分别在OA 、 OB 、 OC 、 OD上,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
A
H
E
G
F
B
D
C
O
答:可通过测量角度来判定,矩形四个角都是直角.请同学们自由发挥,还有什么其他的判定方式.
2.怎样判断四边形的窗框(如图)是不是矩形?说说你的理由.
1.已知:如图,在菱形ABCD中,对角线AC、BD相交点O,E、F、G、H分别是菱形ABCD各边的中点.
求证:OE=OF=OG=OH.
O
E
F
G
H
B
A
C
D
证明:依次连接各个中点,∵四边形ABCD是菱形
∴AC⊥BD
∵点E、H分别是AD、AB的中点
∴EH∥BD
同理EF∥AC
∴EH⊥EF
即∠FEH=90?
∴四边形EFGH是矩形,
矩形对角线相等且互相平分,
∴OE=OF=OG=OH.
D
B
C
A
H
E
F
G
O
证明:菱形面积即为由对角线所切割的四个三角形的面积之和,
∴SABCD=SAOD+SCOD+SABO+SCBO
又上述四个三角形均为直角三角形,
∴SAOD=1/2·AO·DO,
∴SABCD=1/2(AO+CO)(BO+DO),
∴原命题得证.
D
B
C
A
H
E
F
G
O
矩形的判定方法:
有三个角是直角的四边形是矩形 .
A
B
C
D
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
几何语言:
情境二:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:对角线相等的平行四边形是矩形 .
命题:对角线相等的平行四边形是矩形.
已知:平行四边形ABCD,AC=BD.
求证:四边形ABCD是矩形.
A
B
C
D
证明:
∵ AB=CD, BC=BC, AC=BD
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形
∴四边形ABCD是矩形
∴ ∠ABC=∠DCB
对角线相等的平行四边形是矩形 .
矩形的判定方法:
几何语言:
∵四边形ABCD是平行四边形
AC=BD
∴四边形ABCD是矩形
(对角线相等且互相平分的四边形是矩形.)
A
B
C
D
O
(或OA=OC=OB=OD)
你能归纳矩形的几种判定方法吗?
对角线相等的平行四边形是矩形 .
(对角线相等且互相平分的四边形是矩形.)
有三个角是直角的四边形是矩形 .
方法1:
方法2:
证明:∵∠ACB=90°,D是AB的中点,
∴
∵DC=DA,DF平分∠ADC,
∴DF⊥AC,
即 ∠DFC=90°.
同理∠DEC=90°.
∴四边形DECF是矩形(三个角是直角的四边形是矩形)
例2 已知:如图9-22,在△ABC中,∠ACB=90°,D是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.
求证:四边形DECF是矩形.
下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(10)一组邻边垂直,一组对边平行且相等的四边形是矩形;
(9)对角线相等且互相垂直的四边形是矩形;
(8)一组对角互补的平行四边形是矩形;
(4)有三个角都相等的四边形是矩形;
X
X
X
X
如图,M为平行四边形ABCD边AD的中点,且MB=MC,
求证:四边形ABCD是矩形.
A
B
C
D
M
平行四边形ABCD,E是CD的中点, △ABE是等边三角形.
求证:四边形ABCD是矩形.
D
A
B
C
E
知识总结
性质
判定
边
两组对边分别平行
两组对边分别相等
有一个角是直角的平行四边形是矩形
角
矩形的四个角都是直角
有三个角是直角的四边形是矩形
对角线
矩形的两条对角线相等
对角线相等的平行四边形是矩形
(矩形)
有一个角是直角的平行四边形是矩形.
有三个角是直角的四边形是矩形.
两条对角线相等的平行四边形是矩形.
矩形的四个角都是直角.
矩形的对角线相等.
我的收获
谢谢聆听
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
