9.4 矩形、菱形、正方形(第6课时) 课件(共23张PPT)
文档属性
| 名称 | 9.4 矩形、菱形、正方形(第6课时) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 00:00:00 | ||
图片预览




文档简介
第6课时
9.4 矩形、菱形、正方形
第9章 中心对称图形——平行四边形
2020-2021学年度苏科版八年级下册
画一画,猜一猜
请同学们画一个四边形,
要求它既是矩形又是菱形.
正方形
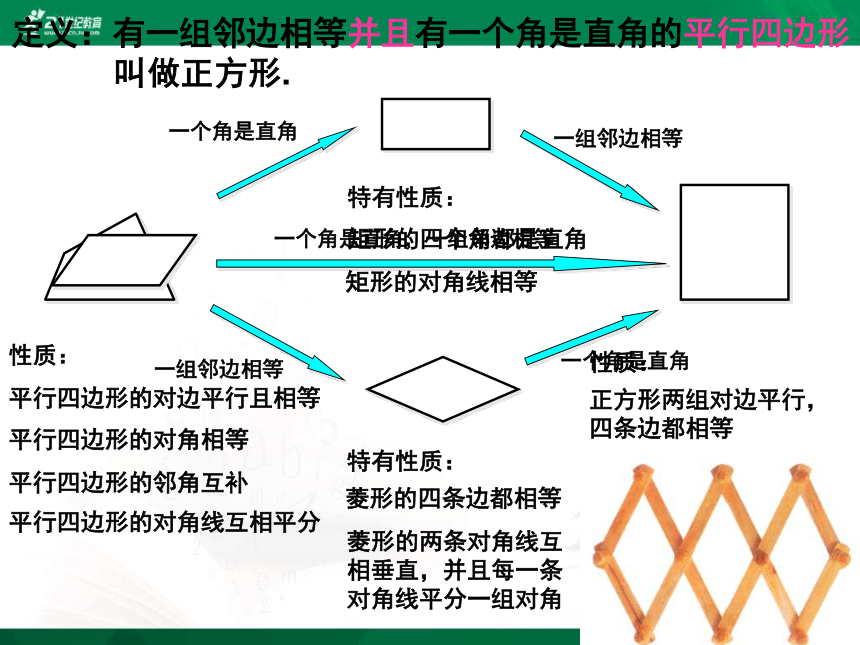
定义:有一组邻边相等并且有一个角是直角的平行四边形
叫做正方形.
一个角是直角
一个角是直角
一个角是直角,一组邻边相等
一组邻边相等
一组邻边相等
平行四边形的对边平行且相等
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的对角线互相平分
性质:
特有性质:
矩形的四个角都是直角
矩形的对角线相等
特有性质:
菱形的四条边都相等
菱形的两条对角线互
相垂直,并且每一条
对角线平分一组对角
性质:
正方形两组对边平行,
四条边都相等
正方形的四个角都是直角
正方形的对角线相等,互
相平分且垂直,并且每一
条对角线平分一组对角
正方形中:(按组说)
1、相等的边有哪些?
2、相等的角有哪些?
3、等腰三角形有哪些?
4、直角三角形有哪些?
5、全等三角形有哪些?
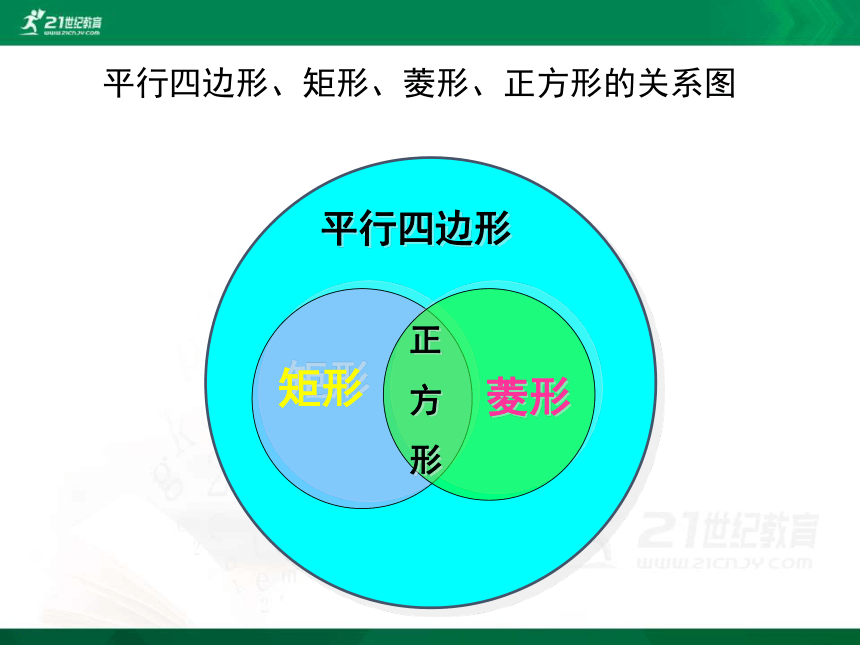
平行四边形
矩形
菱形
正
方
形
平行四边形、矩形、菱形、正方形的关系图
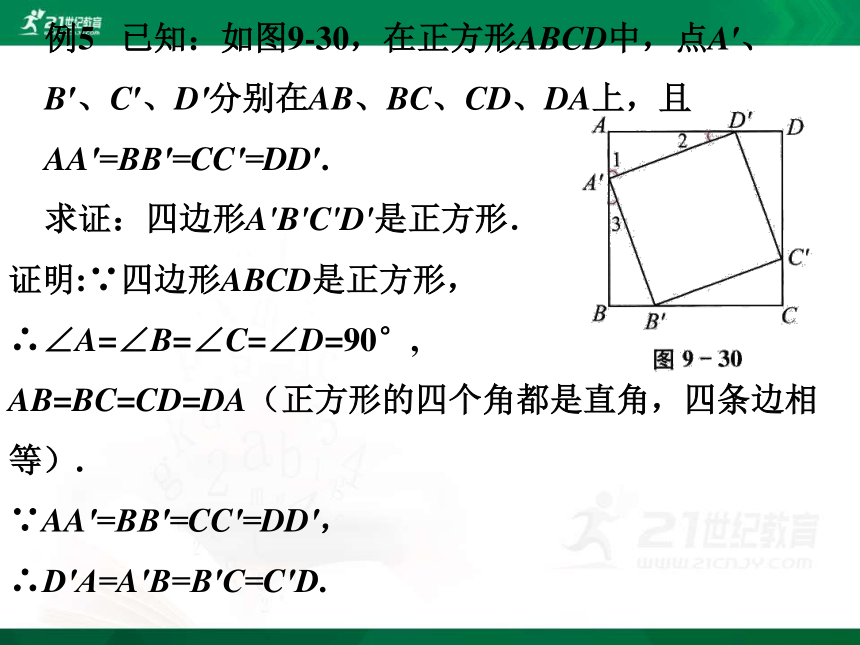
例5 已知:如图9-30,在正方形ABCD中,点A′、
B′、C′、D′分别在AB、BC、CD、DA上,且AA′=BB′=CC′=DD′.
求证:四边形A'B'C'D'是正方形.
证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,
AB=BC=CD=DA(正方形的四个角都是直角,四条边相等).
∵AA′=BB′=CC′=DD′,
∴D′A=A′B=B′C=C′D.
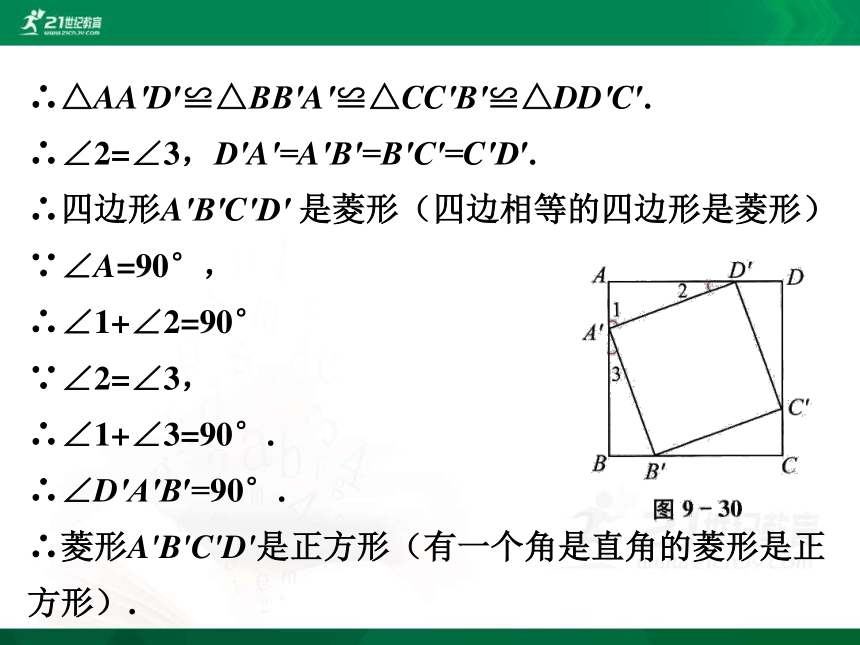
∴△AA′D′≌△BB′A′≌△CC′B′≌△DD′C′.
∴∠2=∠3,D′A′=A′B′=B′C′=C′D′.
∴四边形A′B′C′D′ 是菱形(四边相等的四边形是菱形)
∵∠A=90°,
∴∠1+∠2=90°
∵∠2=∠3,
∴∠1+∠3=90°.
∴∠D′A′B′=90°.
∴菱形A'B'C'D'是正方形(有一个角是直角的菱形是正方形).
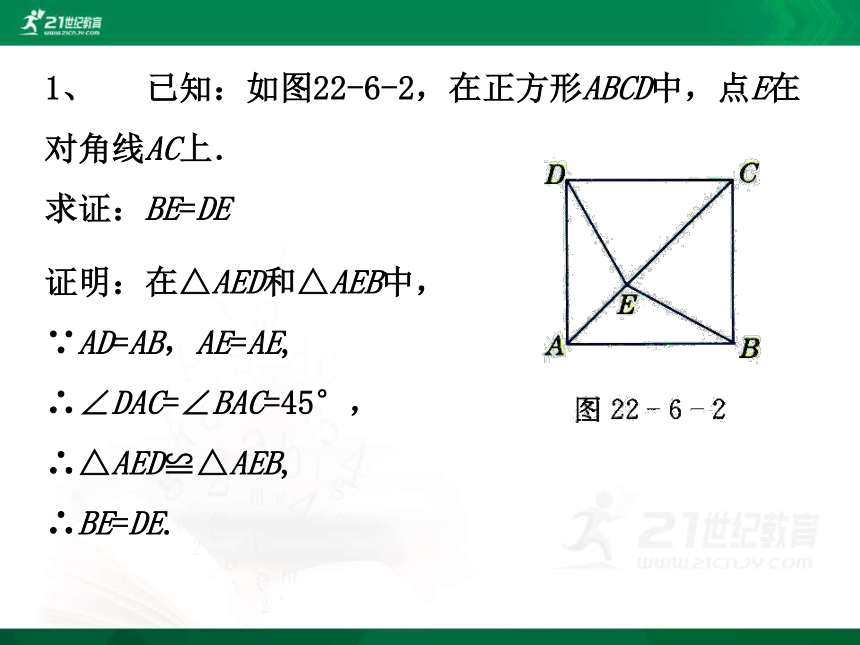
1、 已知:如图22-6-2,在正方形ABCD中,点E在
对角线AC上.
求证:BE=DE
证明:在△AED和△AEB中,
∵AD=AB,AE=AE,
∴∠DAC=∠BAC=45°,
∴△AED≌△AEB,
∴BE=DE.
2、 已知:如图22-6-3,在正方形ABCD中,△BCE是等边三角形.
求证:∠EAD=∠EDA=15°.
证明:∵∠EBC=∠ECB=∠CEB=60°,
∴△ABE,△DCE是等腰三角形,
∠ABE=∠DCE=30°.
∴∠BAE=∠BEA=∠CDE=∠CED=75°.
∴∠EAD=∠EDA=90°-75°=15°.
1、已知:正方形ABCD中,点E、F、G 、H分别是AB、BC、CD、DA的中点,试判断四边形EFGH是正方形吗?为什么?
A
B
C
D
E
F
G
H
定义:有一组邻边相等并且有一个角是直角的平行四边形
叫做正方形.
2、如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等 ?
MN∥AB且MN分别交OA、OB于M、N,
求证:BM=CN.
你能完成证明吗???
AB=BC,∠1=∠2=45 ° 条件够吗?
还需要的条件是 AM=BN
△ABM≌△BCN
你所要证明的两个三角形已经满足
了哪些条件?
由正方形可以得到的条件有:
3、如图(3),正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN.
证明:
∵四边形ABCD是正方形
∴OA=OB ,
∠1=∠2=∠3=45°
又∵MN∥AB
∴∠OMN=∠1=∠3=∠ONM=45°
∴OM=ON
∴OA-OM=OB-ON
即AM=BN
下面大家自己完成证明.
练习1.
已知:正方形ABCD对角线AC、BD相 交于点O,且AB=acm,如图(2).
求:AC的长及正方形的面积S.
练习2.
已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,如图
求:正方形的面积S.
4、已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M,求证:∠MFD=45°
分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____
要证MD=FD,大家只须证得哪两个三角形全等?
试一试
看能不能完成证明???
△CMD≌△ADF
5、已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
证明:
∵CE⊥AF
∴∠ADC=∠AEM=90°
又∵∠CMD=∠AME
∴∠1=∠2
又∵CD=AD,∠ADF=∠MDC
∴Rt△CDM≌Rt△ADF (AAS)
∴DM=DF
下面的证明请大家完成
练习.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H.
求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
6、如图(6),△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N.
求证:∠CEA=∠ABG
分析:欲证∠CEA=∠ABG,
大家想一想证明两个角相等的方法,
你有办法了吗???通过自己的努力,看能不能解决问题?
证明:∵四边形ABDE和四边形ACFG是正方形.
∴AE=AB AG=AC ∠1=∠2=90°
又∵∠EAC=∠1+∠BAC=90°+∠BAC
∠BAG=∠2+∠BAC=90°+∠BAC
∴∠EAC=∠BAG
∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG
7、已知:正方形ABCD中,点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗?为什么?
A
B
C
D
E
F
G
H
求证:矩形的四个角的平分线所围成的四边形是正方形.
在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
谢谢聆听
9.4 矩形、菱形、正方形
第9章 中心对称图形——平行四边形
2020-2021学年度苏科版八年级下册
画一画,猜一猜
请同学们画一个四边形,
要求它既是矩形又是菱形.
正方形
定义:有一组邻边相等并且有一个角是直角的平行四边形
叫做正方形.
一个角是直角
一个角是直角
一个角是直角,一组邻边相等
一组邻边相等
一组邻边相等
平行四边形的对边平行且相等
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的对角线互相平分
性质:
特有性质:
矩形的四个角都是直角
矩形的对角线相等
特有性质:
菱形的四条边都相等
菱形的两条对角线互
相垂直,并且每一条
对角线平分一组对角
性质:
正方形两组对边平行,
四条边都相等
正方形的四个角都是直角
正方形的对角线相等,互
相平分且垂直,并且每一
条对角线平分一组对角
正方形中:(按组说)
1、相等的边有哪些?
2、相等的角有哪些?
3、等腰三角形有哪些?
4、直角三角形有哪些?
5、全等三角形有哪些?
平行四边形
矩形
菱形
正
方
形
平行四边形、矩形、菱形、正方形的关系图
例5 已知:如图9-30,在正方形ABCD中,点A′、
B′、C′、D′分别在AB、BC、CD、DA上,且AA′=BB′=CC′=DD′.
求证:四边形A'B'C'D'是正方形.
证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,
AB=BC=CD=DA(正方形的四个角都是直角,四条边相等).
∵AA′=BB′=CC′=DD′,
∴D′A=A′B=B′C=C′D.
∴△AA′D′≌△BB′A′≌△CC′B′≌△DD′C′.
∴∠2=∠3,D′A′=A′B′=B′C′=C′D′.
∴四边形A′B′C′D′ 是菱形(四边相等的四边形是菱形)
∵∠A=90°,
∴∠1+∠2=90°
∵∠2=∠3,
∴∠1+∠3=90°.
∴∠D′A′B′=90°.
∴菱形A'B'C'D'是正方形(有一个角是直角的菱形是正方形).
1、 已知:如图22-6-2,在正方形ABCD中,点E在
对角线AC上.
求证:BE=DE
证明:在△AED和△AEB中,
∵AD=AB,AE=AE,
∴∠DAC=∠BAC=45°,
∴△AED≌△AEB,
∴BE=DE.
2、 已知:如图22-6-3,在正方形ABCD中,△BCE是等边三角形.
求证:∠EAD=∠EDA=15°.
证明:∵∠EBC=∠ECB=∠CEB=60°,
∴△ABE,△DCE是等腰三角形,
∠ABE=∠DCE=30°.
∴∠BAE=∠BEA=∠CDE=∠CED=75°.
∴∠EAD=∠EDA=90°-75°=15°.
1、已知:正方形ABCD中,点E、F、G 、H分别是AB、BC、CD、DA的中点,试判断四边形EFGH是正方形吗?为什么?
A
B
C
D
E
F
G
H
定义:有一组邻边相等并且有一个角是直角的平行四边形
叫做正方形.
2、如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等 ?
MN∥AB且MN分别交OA、OB于M、N,
求证:BM=CN.
你能完成证明吗???
AB=BC,∠1=∠2=45 ° 条件够吗?
还需要的条件是 AM=BN
△ABM≌△BCN
你所要证明的两个三角形已经满足
了哪些条件?
由正方形可以得到的条件有:
3、如图(3),正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN.
证明:
∵四边形ABCD是正方形
∴OA=OB ,
∠1=∠2=∠3=45°
又∵MN∥AB
∴∠OMN=∠1=∠3=∠ONM=45°
∴OM=ON
∴OA-OM=OB-ON
即AM=BN
下面大家自己完成证明.
练习1.
已知:正方形ABCD对角线AC、BD相 交于点O,且AB=acm,如图(2).
求:AC的长及正方形的面积S.
练习2.
已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,如图
求:正方形的面积S.
4、已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M,求证:∠MFD=45°
分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____
要证MD=FD,大家只须证得哪两个三角形全等?
试一试
看能不能完成证明???
△CMD≌△ADF
5、已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
证明:
∵CE⊥AF
∴∠ADC=∠AEM=90°
又∵∠CMD=∠AME
∴∠1=∠2
又∵CD=AD,∠ADF=∠MDC
∴Rt△CDM≌Rt△ADF (AAS)
∴DM=DF
下面的证明请大家完成
练习.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H.
求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
6、如图(6),△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N.
求证:∠CEA=∠ABG
分析:欲证∠CEA=∠ABG,
大家想一想证明两个角相等的方法,
你有办法了吗???通过自己的努力,看能不能解决问题?
证明:∵四边形ABDE和四边形ACFG是正方形.
∴AE=AB AG=AC ∠1=∠2=90°
又∵∠EAC=∠1+∠BAC=90°+∠BAC
∠BAG=∠2+∠BAC=90°+∠BAC
∴∠EAC=∠BAG
∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG
7、已知:正方形ABCD中,点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗?为什么?
A
B
C
D
E
F
G
H
求证:矩形的四个角的平分线所围成的四边形是正方形.
在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
谢谢聆听
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
