9.4 矩形、菱形、正方形(第5课时) 课件(共23张PPT)
文档属性
| 名称 | 9.4 矩形、菱形、正方形(第5课时) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 00:00:00 | ||
图片预览



文档简介
第5课时
9.4 矩形、菱形、正方形
第9章 中心对称图形——平行四边形
2020-2021学年度苏科版八年级下册
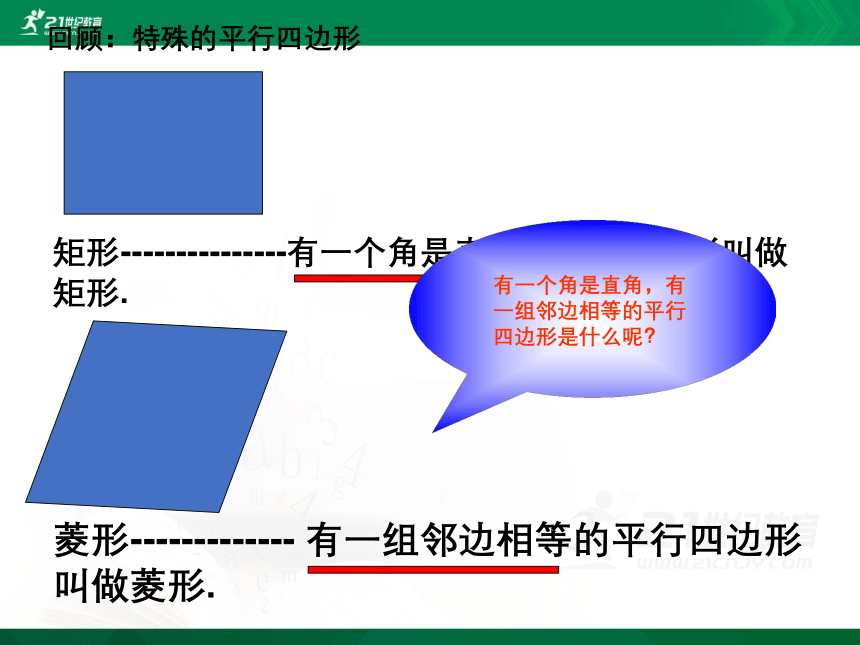
回顾:特殊的平行四边形
矩形---------------有一个角是直角的平行四边形叫做矩形.
菱形------------- 有一组邻边相等的平行四边形叫做菱形.
有一个角是直角,有一组邻边相等的平行四边形是什么呢?
正方形的定义:
有一组邻边相等并且有一个角是直角的平行四边形.
正方形
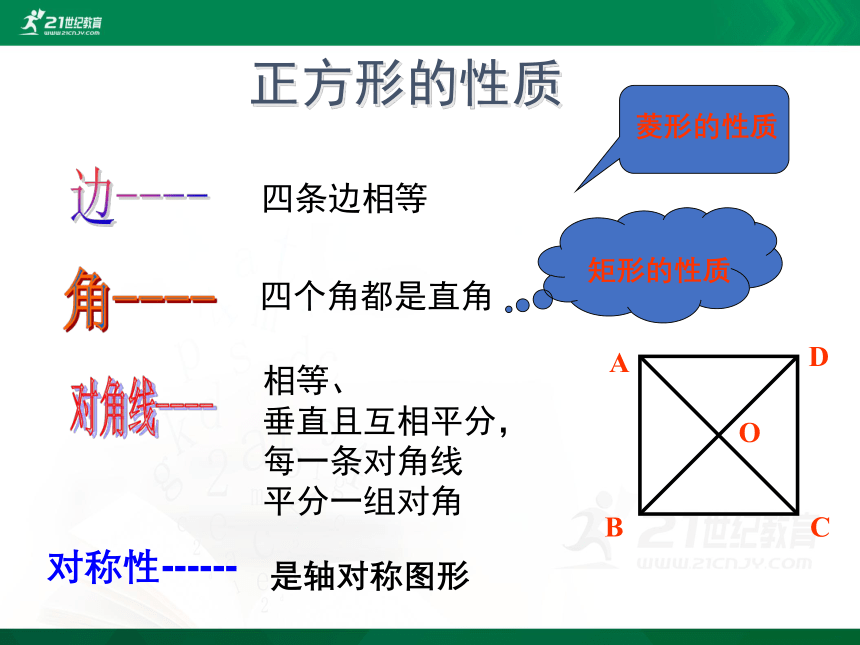
正方形的性质
四条边相等
四个角都是直角
相等、
垂直且互相平分,
每一条对角线
平分一组对角
A
B
C
D
O
边----
角----
对角线----
菱形的性质
矩形的性质
对称性------
是轴对称图形
正方形是轴对称图形,它的对称轴是什么?
快速抢答
根据图形所具有的性质,在下表相应的空格中打”√”
平行四边形
矩形
菱形
正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
体会正方形的完美
正方形不但具备一般的平行四边形的性质,而且同时具备矩形和菱形的性质.
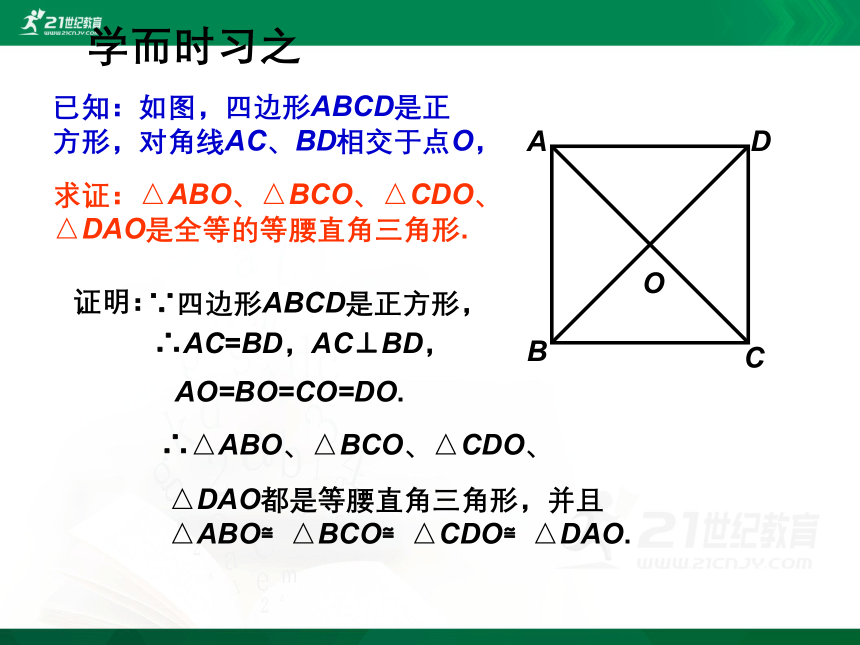
求证:△ABO、△BCO、△CDO、
△DAO是全等的等腰直角三角形.
△DAO都是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.
A
B
C
D
O
已知:如图,四边形ABCD是正
方形,对角线AC、BD相交于点O,
学而时习之
证明:
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
AO=BO=CO=DO.
∴△ABO、△BCO、△CDO、
矩形
菱形
正方形
有一组邻边相等
有一个角是直角
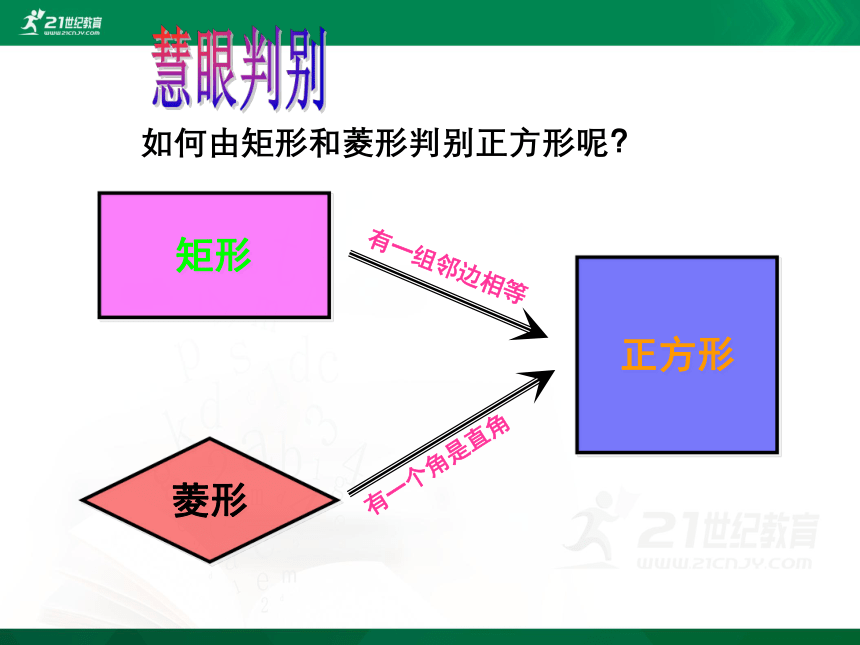
慧眼判别
如何由矩形和菱形判别正方形呢?
一组邻边相等
有一个内角是直角
一组邻边相等
有一个内角是直角
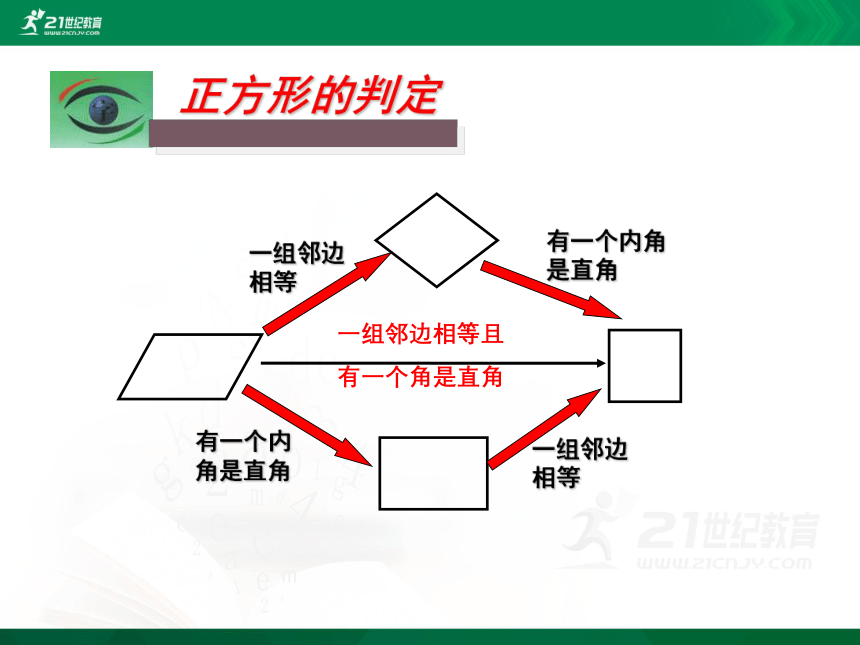
正方形的判定
一组邻边相等且
有一个角是直角
例5 已知:如图9-30,在正方形ABCD中,点A′、
B′、C′、D′分别在AB、BC、CD、DA上,且AA′=BB′=CC′=DD′.
求证:四边形A'B'C'D'是正方形.
证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,
AB=BC=CD=DA(正方形的四个角都是直角,四条边相等).
∵AA′=BB′=CC′=DD′,
∴D′A=A′B=B′C=C′D.
∴△AA′D′≌△BB′A′≌△CC′B′≌△DD′C′.
∴∠2=∠3,
D′A′=A′B′=B′C′=C′D′.
∴四边形A′B′C′D′ 是菱形(四边相等的四边形是菱形)
∵∠A=90°,
∴∠1+∠2=90°
∵∠2=∠3,
∴∠1+∠3=90°.
∴∠D′A′B′=90°.
∴菱形A'B'C'D'是正方形(有一个角是直角的菱形是正方形).
1 、 已知:如图22-6-2,在正方形ABCD中,点E在
对角线AC上.
求证:BE=DE
证明:在△AED和△AEB中,
∵AD=AB,AE=AE,
∴∠DAC=∠BAC=45°,
∴△AED≌△AEB,
∴BE=DE.
2、 已知:如图22-6-3,在正方形ABCD中,△BCE是等边三角形.
求证:∠EAD=∠EDA=15°.
证明:∵∠EBC=∠ECB=∠CEB=60°,
∴△ABE,△DCE是等腰三角形,
∠ABE=∠DCE=30°.
∴∠BAE=∠BEA=∠CDE=∠CED=75°.
∴∠EAD=∠EDA=90°-75°=15°.
证明:对角线互相垂直的平行四边形是菱形.
A
B
C
D
O
已知:平行四边形ABCD的对角线互相垂直.
求证:平行四边形ABCD是菱形.
证明:已知平行四边形ABCD
∵它是平行四边形 ∴AB=CD, BC=AD
又∵平行四边形对角线相互平分 ∴BO=DO
∵AO=OA,BO=DO,∠AOB=90°=∠AOD
∴△AOB≌△AOD
∴AB=AD
又∵AB=CD,BC=AD ∴AB=BC=CD=DA
即平行四边形ABCD是菱形.
证明:有三个角是直角的四边形是矩形.
A
B
C
D
已知:四边形ABCD中,∠A=∠B=∠C=90°.求证:四边形ABCD是矩形.
证明:
∵∠A=∠B=∠C=90°
∴AD∥BC,AB∥CD
∴四边形ABCD是平行四边形(同旁内角互补,两直线平行)
又∵∠A=90°
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形).
如图,矩形ABCD的两条对角线相交于点O,已知∠AOD=120?,AB=2.5cm,求矩形对角线的长.
A
C
D
B
O
证明:∵∠AOD=120?→∠AOB=60?
→△ABO是等边三角形
∴OA=AB=OB→OA=2.5 cm
∴AC=2OA=2×2.5=5cm
即矩形对角线的长是5cm.
学而应用之
1.从长方形木板中怎样截出最大的正方形木板?
2.怎样使菱形的衣帽架变成正方形的衣帽架?
3.现有一条方巾,想请同学们帮助检验一下方巾是否是正方形的.怎样检验?
平行四边形
矩形
菱形
正
方
形
平行四边形、矩形、菱形、正方形的包含关系
想一想
谢谢聆听
9.4 矩形、菱形、正方形
第9章 中心对称图形——平行四边形
2020-2021学年度苏科版八年级下册
回顾:特殊的平行四边形
矩形---------------有一个角是直角的平行四边形叫做矩形.
菱形------------- 有一组邻边相等的平行四边形叫做菱形.
有一个角是直角,有一组邻边相等的平行四边形是什么呢?
正方形的定义:
有一组邻边相等并且有一个角是直角的平行四边形.
正方形
正方形的性质
四条边相等
四个角都是直角
相等、
垂直且互相平分,
每一条对角线
平分一组对角
A
B
C
D
O
边----
角----
对角线----
菱形的性质
矩形的性质
对称性------
是轴对称图形
正方形是轴对称图形,它的对称轴是什么?
快速抢答
根据图形所具有的性质,在下表相应的空格中打”√”
平行四边形
矩形
菱形
正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
体会正方形的完美
正方形不但具备一般的平行四边形的性质,而且同时具备矩形和菱形的性质.
求证:△ABO、△BCO、△CDO、
△DAO是全等的等腰直角三角形.
△DAO都是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.
A
B
C
D
O
已知:如图,四边形ABCD是正
方形,对角线AC、BD相交于点O,
学而时习之
证明:
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
AO=BO=CO=DO.
∴△ABO、△BCO、△CDO、
矩形
菱形
正方形
有一组邻边相等
有一个角是直角
慧眼判别
如何由矩形和菱形判别正方形呢?
一组邻边相等
有一个内角是直角
一组邻边相等
有一个内角是直角
正方形的判定
一组邻边相等且
有一个角是直角
例5 已知:如图9-30,在正方形ABCD中,点A′、
B′、C′、D′分别在AB、BC、CD、DA上,且AA′=BB′=CC′=DD′.
求证:四边形A'B'C'D'是正方形.
证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,
AB=BC=CD=DA(正方形的四个角都是直角,四条边相等).
∵AA′=BB′=CC′=DD′,
∴D′A=A′B=B′C=C′D.
∴△AA′D′≌△BB′A′≌△CC′B′≌△DD′C′.
∴∠2=∠3,
D′A′=A′B′=B′C′=C′D′.
∴四边形A′B′C′D′ 是菱形(四边相等的四边形是菱形)
∵∠A=90°,
∴∠1+∠2=90°
∵∠2=∠3,
∴∠1+∠3=90°.
∴∠D′A′B′=90°.
∴菱形A'B'C'D'是正方形(有一个角是直角的菱形是正方形).
1 、 已知:如图22-6-2,在正方形ABCD中,点E在
对角线AC上.
求证:BE=DE
证明:在△AED和△AEB中,
∵AD=AB,AE=AE,
∴∠DAC=∠BAC=45°,
∴△AED≌△AEB,
∴BE=DE.
2、 已知:如图22-6-3,在正方形ABCD中,△BCE是等边三角形.
求证:∠EAD=∠EDA=15°.
证明:∵∠EBC=∠ECB=∠CEB=60°,
∴△ABE,△DCE是等腰三角形,
∠ABE=∠DCE=30°.
∴∠BAE=∠BEA=∠CDE=∠CED=75°.
∴∠EAD=∠EDA=90°-75°=15°.
证明:对角线互相垂直的平行四边形是菱形.
A
B
C
D
O
已知:平行四边形ABCD的对角线互相垂直.
求证:平行四边形ABCD是菱形.
证明:已知平行四边形ABCD
∵它是平行四边形 ∴AB=CD, BC=AD
又∵平行四边形对角线相互平分 ∴BO=DO
∵AO=OA,BO=DO,∠AOB=90°=∠AOD
∴△AOB≌△AOD
∴AB=AD
又∵AB=CD,BC=AD ∴AB=BC=CD=DA
即平行四边形ABCD是菱形.
证明:有三个角是直角的四边形是矩形.
A
B
C
D
已知:四边形ABCD中,∠A=∠B=∠C=90°.求证:四边形ABCD是矩形.
证明:
∵∠A=∠B=∠C=90°
∴AD∥BC,AB∥CD
∴四边形ABCD是平行四边形(同旁内角互补,两直线平行)
又∵∠A=90°
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形).
如图,矩形ABCD的两条对角线相交于点O,已知∠AOD=120?,AB=2.5cm,求矩形对角线的长.
A
C
D
B
O
证明:∵∠AOD=120?→∠AOB=60?
→△ABO是等边三角形
∴OA=AB=OB→OA=2.5 cm
∴AC=2OA=2×2.5=5cm
即矩形对角线的长是5cm.
学而应用之
1.从长方形木板中怎样截出最大的正方形木板?
2.怎样使菱形的衣帽架变成正方形的衣帽架?
3.现有一条方巾,想请同学们帮助检验一下方巾是否是正方形的.怎样检验?
平行四边形
矩形
菱形
正
方
形
平行四边形、矩形、菱形、正方形的包含关系
想一想
谢谢聆听
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
