9.4 矩形、菱形、正方形(第3课时) 课件(共26张PPT)
文档属性
| 名称 | 9.4 矩形、菱形、正方形(第3课时) 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 20:30:11 | ||
图片预览




文档简介
第3课时
9.4 矩形、菱形、正方形
第9章 中心对称图形——平行四边形
2020-2021学年度苏科版八年级下册
菱 形
平行四边形
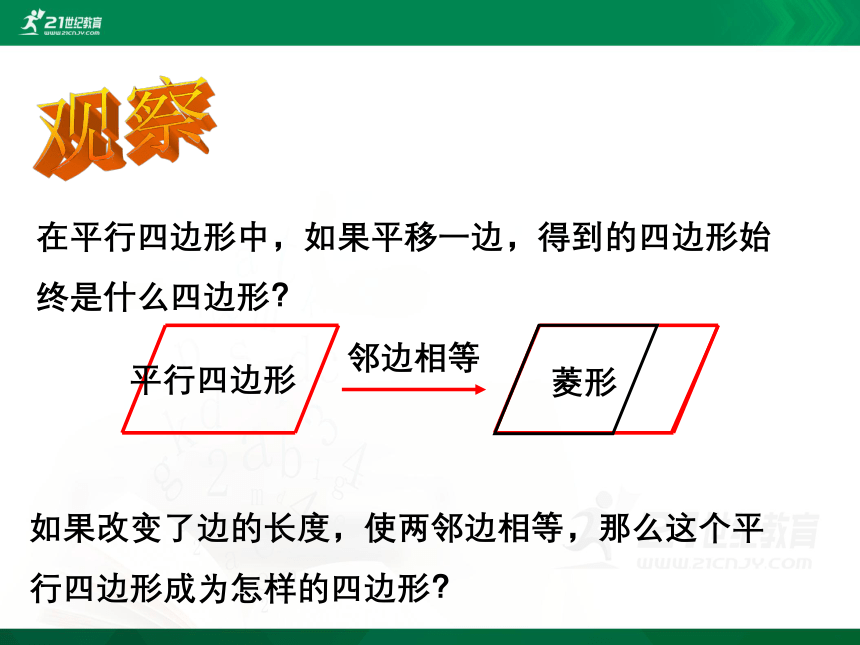
邻边相等
菱形
在平行四边形中,如果平移一边,得到的四边形始终是什么四边形?
观察
如果改变了边的长度,使两邻边相等,那么这个平行四边形成为怎样的四边形?
感受
生活
让我们一同走进生活中的菱形
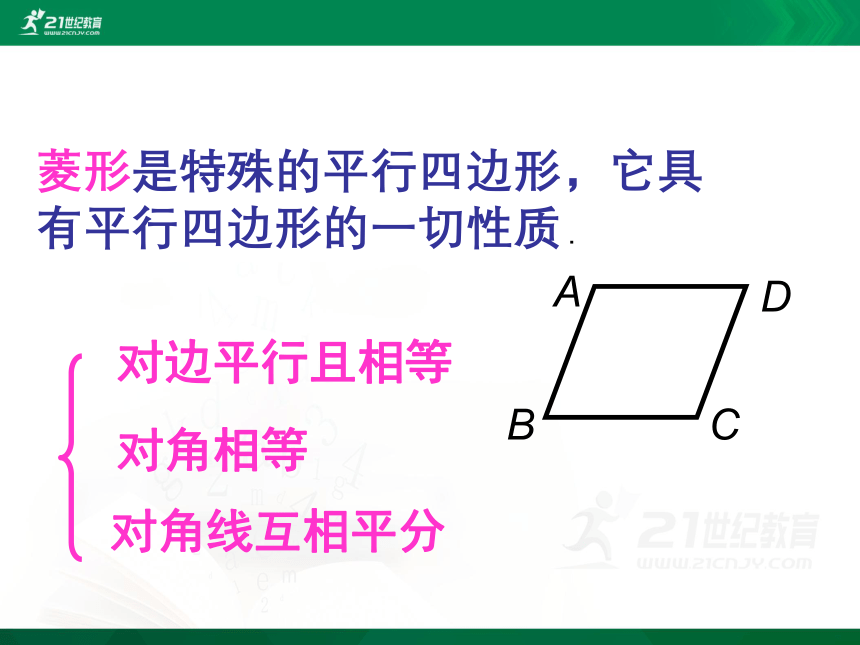
对边平行且相等
对角相等
对角线互相平分
A
B
D
C
菱形是特殊的平行四边形,它具有平行四边形的一切性质.
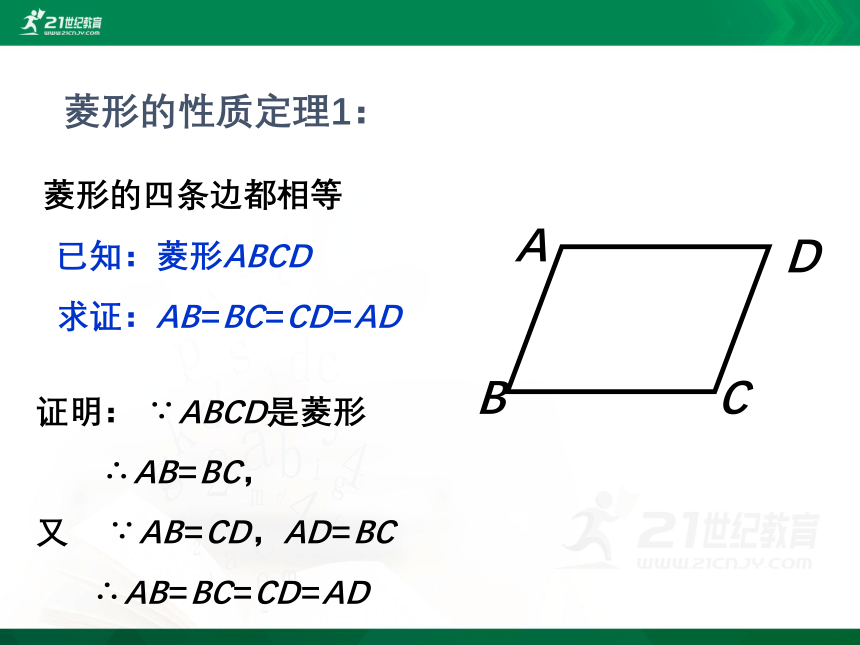
菱形的性质定理1:
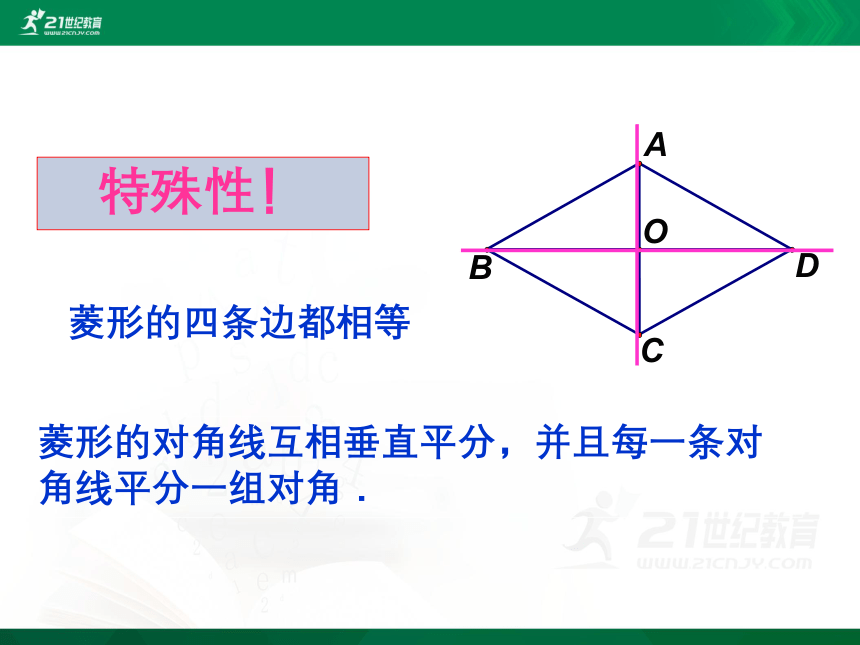
菱形的四条边都相等
已知:菱形ABCD
求证:AB=BC=CD=AD
证明: ∵ABCD是菱形
∴AB=BC,
又 ∵AB=CD,AD=BC
∴AB=BC=CD=AD
A
B
D
C
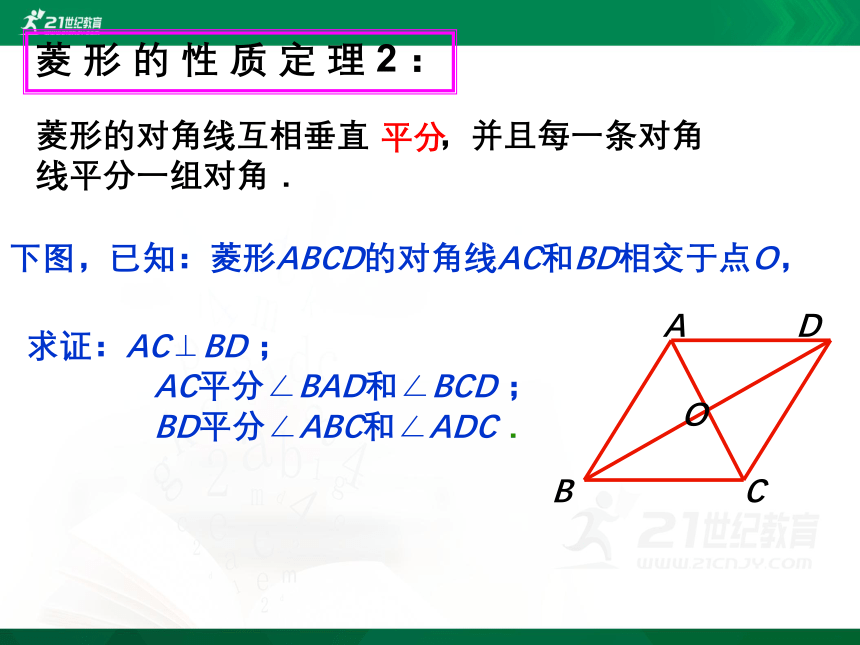
下图,已知:菱形ABCD的对角线AC和BD相交于点O,
A
B
C
D
O
求证:AC⊥BD ;
AC平分∠BAD和∠BCD ;
BD平分∠ABC和∠ADC.
菱形的对角线互相垂直 ,并且每一条对角线平分一组对角.
平分
菱形的性质定理2:
菱形的四条边都相等
菱形的对角线互相垂直平分,并且每一条对角线平分一组对角.
D
O
A
C
B
特殊性!
例3 如图9-25,木制活动衣帽架由3个全等的菱形构成,在A、E、F、C、G、H处安装上、下两排挂钩,可以根据需要改变挂钩间的距离,并在B、M处固定.已知菱形ABCD的边长为13cm,要使两排挂钩间的距离为24cm,求B、M之间的距离.
解:如图9-26,连接AC、BD,AC与BD相交于点O.
∵四边形ABCD是菱形,
∴∠AOB=90°,
(菱形的对角线互相垂直平分)
∴
∴ (菱形的对角线互相平分)
B、M之间的距离是30cm.
解 在菱形ABCD中,
AB=AD(根据什么?),
AC平分∠BAD(菱形的每条对角线平分一组对角).
又∵∠BAC=30°,
∴∠BAD=60°,
∴△ABD是等边三角形,
∴AB=BD=6.
又∵AC⊥BD(菱形的对角线互相垂直),
由勾股定理,得
如图,在菱形ABCD中,对角线AC,BD相交于点O,∠BAC=30°,BD=6.求菱形的边长和对角线AC的长.
D
A
B
C
O
30°
菱形的判定方法:
一组邻边相等的平行四边形是菱形;
AB=BC
A
B
C
D
□ABCD
A
B
C
D
菱形ABCD
AB=BC
□ABCD
四边形ABCD是菱形
情境:李芳同学先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?
猜想:四边都相等的四边形是菱形 .
命题:对角线互相垂直的平行四边形是菱形.
已知: 中,AC ⊥ BD
ABCD
ABCD
求证: 是菱形
A
B
C
D
O
菱形的判定定理:
对角线互相垂直的平行四边形是菱形;
AC⊥BD
AC⊥BD
□ABCD
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
四边形ABCD是菱形
(对角线互相垂直平分的四边形是菱形)
归纳
菱形常用的判定方法:
1.有一组邻边相等的平行四边形叫做菱形.
2.对角线互相垂直的平行四边形是菱形.
(对角线互相垂直平分的四边形是菱形.)
3.有四条边相等的四边形是菱形.
证明:∵AD//BC,
∴∠1=∠2.
∵EF垂直平分AC,
∴OA=OC,∠AOE=∠COF.
∴△AOE≌△COF.
∴OE=OF.
∴四边形AFCE是平行四边形(对角线互相平分的四边形是平行四边形).
又∵ EF ⊥ AC,
∴四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形).
例4 已知:如图9-28,在四边形ABCD中,AD//BC,
对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
求证:四边形AFCE是菱形.
判断下列命题是否正确,并说明理由.
(1)对角线互相平分且邻边相等的四边形是菱形.
(2)两组对边分别平行且一组邻边相等的四边形是菱形.
(3) 两组对角分别相等且对角线互相垂直的四边形是菱形.
(4)对角线互相垂直平分的四边形是菱形.
一边长为5cm平行四边形的两条对角线的长分别为6cm和8cm,求证:这个平行四边形为菱形.
A
B
C
D
请你动脑筋
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
A
C
D
B
思考:
D
C
B
A
如图,AD∥BC,BD垂直平分AC,四边形ABCD一定是菱形吗?若是,请说明理由.
C
D
B
A
O
思考题:
┐
) 1
2 (
如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,说明CE⊥DF.
A
B
F
N
D
M
E
C
学到了如何识别菱形
? 今天你学到了什么 ?
菱形识别方法:
1、一组邻边相等的平行四边形是菱形
2、对角线互相垂直的平行四边形是菱形
3、四条边都相等的四边形是菱形
B
D
A
C
谢谢聆听
9.4 矩形、菱形、正方形
第9章 中心对称图形——平行四边形
2020-2021学年度苏科版八年级下册
菱 形
平行四边形
邻边相等
菱形
在平行四边形中,如果平移一边,得到的四边形始终是什么四边形?
观察
如果改变了边的长度,使两邻边相等,那么这个平行四边形成为怎样的四边形?
感受
生活
让我们一同走进生活中的菱形
对边平行且相等
对角相等
对角线互相平分
A
B
D
C
菱形是特殊的平行四边形,它具有平行四边形的一切性质.
菱形的性质定理1:
菱形的四条边都相等
已知:菱形ABCD
求证:AB=BC=CD=AD
证明: ∵ABCD是菱形
∴AB=BC,
又 ∵AB=CD,AD=BC
∴AB=BC=CD=AD
A
B
D
C
下图,已知:菱形ABCD的对角线AC和BD相交于点O,
A
B
C
D
O
求证:AC⊥BD ;
AC平分∠BAD和∠BCD ;
BD平分∠ABC和∠ADC.
菱形的对角线互相垂直 ,并且每一条对角线平分一组对角.
平分
菱形的性质定理2:
菱形的四条边都相等
菱形的对角线互相垂直平分,并且每一条对角线平分一组对角.
D
O
A
C
B
特殊性!
例3 如图9-25,木制活动衣帽架由3个全等的菱形构成,在A、E、F、C、G、H处安装上、下两排挂钩,可以根据需要改变挂钩间的距离,并在B、M处固定.已知菱形ABCD的边长为13cm,要使两排挂钩间的距离为24cm,求B、M之间的距离.
解:如图9-26,连接AC、BD,AC与BD相交于点O.
∵四边形ABCD是菱形,
∴∠AOB=90°,
(菱形的对角线互相垂直平分)
∴
∴ (菱形的对角线互相平分)
B、M之间的距离是30cm.
解 在菱形ABCD中,
AB=AD(根据什么?),
AC平分∠BAD(菱形的每条对角线平分一组对角).
又∵∠BAC=30°,
∴∠BAD=60°,
∴△ABD是等边三角形,
∴AB=BD=6.
又∵AC⊥BD(菱形的对角线互相垂直),
由勾股定理,得
如图,在菱形ABCD中,对角线AC,BD相交于点O,∠BAC=30°,BD=6.求菱形的边长和对角线AC的长.
D
A
B
C
O
30°
菱形的判定方法:
一组邻边相等的平行四边形是菱形;
AB=BC
A
B
C
D
□ABCD
A
B
C
D
菱形ABCD
AB=BC
□ABCD
四边形ABCD是菱形
情境:李芳同学先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?
猜想:四边都相等的四边形是菱形 .
命题:对角线互相垂直的平行四边形是菱形.
已知: 中,AC ⊥ BD
ABCD
ABCD
求证: 是菱形
A
B
C
D
O
菱形的判定定理:
对角线互相垂直的平行四边形是菱形;
AC⊥BD
AC⊥BD
□ABCD
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
四边形ABCD是菱形
(对角线互相垂直平分的四边形是菱形)
归纳
菱形常用的判定方法:
1.有一组邻边相等的平行四边形叫做菱形.
2.对角线互相垂直的平行四边形是菱形.
(对角线互相垂直平分的四边形是菱形.)
3.有四条边相等的四边形是菱形.
证明:∵AD//BC,
∴∠1=∠2.
∵EF垂直平分AC,
∴OA=OC,∠AOE=∠COF.
∴△AOE≌△COF.
∴OE=OF.
∴四边形AFCE是平行四边形(对角线互相平分的四边形是平行四边形).
又∵ EF ⊥ AC,
∴四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形).
例4 已知:如图9-28,在四边形ABCD中,AD//BC,
对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
求证:四边形AFCE是菱形.
判断下列命题是否正确,并说明理由.
(1)对角线互相平分且邻边相等的四边形是菱形.
(2)两组对边分别平行且一组邻边相等的四边形是菱形.
(3) 两组对角分别相等且对角线互相垂直的四边形是菱形.
(4)对角线互相垂直平分的四边形是菱形.
一边长为5cm平行四边形的两条对角线的长分别为6cm和8cm,求证:这个平行四边形为菱形.
A
B
C
D
请你动脑筋
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
A
C
D
B
思考:
D
C
B
A
如图,AD∥BC,BD垂直平分AC,四边形ABCD一定是菱形吗?若是,请说明理由.
C
D
B
A
O
思考题:
┐
) 1
2 (
如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,说明CE⊥DF.
A
B
F
N
D
M
E
C
学到了如何识别菱形
? 今天你学到了什么 ?
菱形识别方法:
1、一组邻边相等的平行四边形是菱形
2、对角线互相垂直的平行四边形是菱形
3、四条边都相等的四边形是菱形
B
D
A
C
谢谢聆听
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
