鸡免同笼

(共36张PPT)
东郭中学 李曼
第七章第三节
说教材之地位和作用
本课是北师大版8年级（上册）第七章 二元一次方程组第三节的内容，是在学习了二元一次方程组的概念及其解法之后的进一步延伸。由以前七年级的一元一次方程过渡到现在学习的二元一次方程组解决实际应用问题，首先就要把实际应用问题准确的转化为方程问题。通过理解+练习+巩固，让学生进一步感受用方程建模思想可以解决实际应用问题，充分感受数学来源于生活并用于生活。 同时，为今后学习一般线性方程及平面解析几何等知识打下基础，在教材中起到承前启后的作用。
说教材之学情分析
在此之前，学生已经能用算术法和一元一次方程解决实际应用问题，具备一定的分析问题和解决问题的能力，现在也掌握了二元一次方程组的解法——代入法和加减法。但是担心学生在解决应用题时，有时会思维定势把思维方向定在算术方法或一元一次方程方法上，而不知道学以致用正在学习的二元一次方程组思想。
说教材之教学目标分析
a.知识目标——经历和体验列方程组解决实际问题的过程，进一步体会方程（组）是
刻画现实世界的有效数学模型。
b.能力目标——培养学生列方程组解决实际问题的意识，增强学生的数学应用能力。
c.情感目标——了解我国古代数学的光辉成就，增强民族自豪感； 提高学生对数学的好奇心和求知欲；增强学数学的自信心。
d.教学重点——通过不同方法研究解决鸡兔同笼相关问题，使学生理解并掌握类似问题的
解题方法。增强学生的数学理解能力。
e.教学难点———引导学生根据题意寻求等量关系，再用未知量表示出代替等量关系的方程组。
说教法和学法
1.教学中主要采用探究发现法、小组合作讨
论法和参与互动交流法。
2.强调学生是学习的主人，在学习过程中
尽可能多的为学生提供探索和交流的空
间，鼓励学生自主探索与合作交流。
3.展示大量古题图片，激发学生的好奇心和求知欲，增加学习数学的兴趣，体会数学发展的历史。
4.在问题解决过程中提升数学方法，从而丰富学生的数学思想，逐步建立完善认知结构。
说教学过程环节设计
1.情境导入，激发兴趣 ——通过一系列古题图片让学生体 会数学方程建模思想。
2.自主讨论，古题今解 ——将学生分为六组进行自主讨论，然后各推选一人来板书演示该组的解题方法，师生评选出“智慧之星”。
3.闯关游戏，合作共进—— 对六个组合作成果即不同的解题方法进行评比，选出 “智慧小组” ，给予热烈的掌声鼓励。
4.高手过招，益智生活 —— 要求学生做几个难度较大的类似题目，递进加深用二元一次方程组解决实际问题的理解。
5.小结收获，作业反思—— 让学生对所学内容谈谈心得。老师对学生的发言进行归纳概括。
《孙子算经》是我国古代一部较为普及的算书,许多问题浅显有趣,其中下卷第31题”雉兔同笼”流传尤为广泛,飘洋过海流传到了日本等国.
情境导入：
“鸡兔同笼”题为:
今有鸡兔同笼,
上有三十五头,
下有九十四足,
问鸡兔各几何
“上有三十五头”的意思是什么
“下有九十四足”的意思是什么
方程
一元
二元
自主探索
解：设有鸡x只，则有兔（35–x）只.由题意，得
答：有鸡23只，有兔12只.
所以有兔（35-23）只，即有12只.
返回
方法一：
35
94
足
头
总数
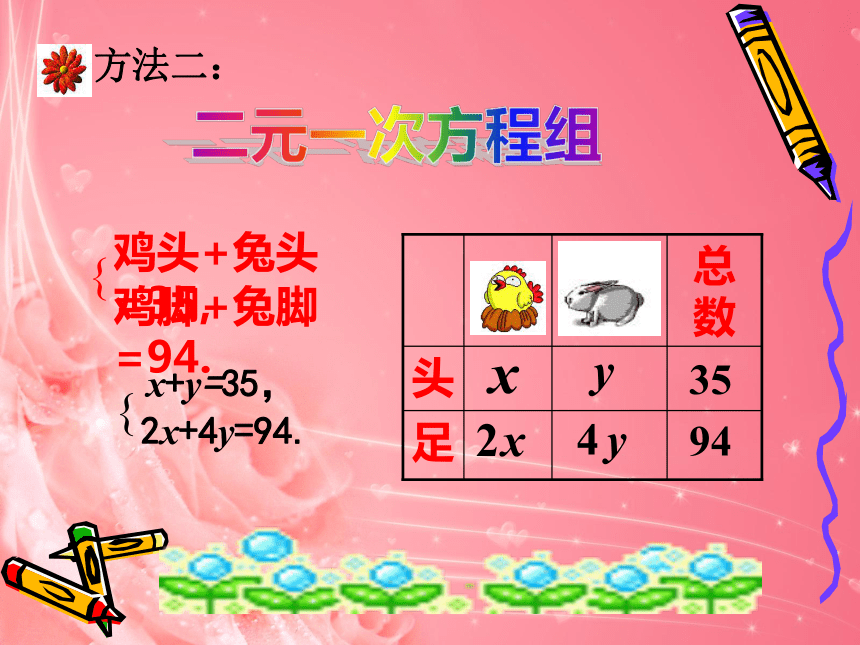
鸡头+兔头=35,
鸡脚+兔脚=94.
{
x+y=35，
2x+4y=94.
{
方法二：
解：设有鸡x只，有兔y只.由题意，得
①
②
把y=12代入①，得x=23.
答：有鸡23只，有兔12只.
把 ①化为
代入②，得：
=35-y
代入消元
由一学生板书：
解：设鸡为x 只,兔为y 只.则
①×2 得： 2x+2y=70， ③
②-③ 得： 2y=24，
y=12.
把 y=12 代入①，得：x=23.
答：有鸡23只，兔12只.
x+y=35， ①
2x+4y=94. ②
原方程组的解是
x=23,
y=12.
加减消元
返回
由另一学生板书：
你觉得哪种方法好呢？为什么？
合作交流：
今有牛五、羊二，直金十两．牛二、羊五，直金八两．牛、羊各直金几何？
小组探究
5头牛、2只羊共价值10两“金”；2头牛、5只羊共价值8两“金”.问每头牛、每只羊各价值多少“金”？
解：设每头牛价值为x两，每只羊价值y两.
5x+2y=10,
2x+5y=8.
{
解得
x=
y=
{
答:羊值”金” 两,牛值”金” 两.
以绳测井
若将绳三折测之，绳多五尺；
若将绳四折测之，绳多一尺.
绳长、井深各几何？
以绳测井
若将绳三折测之，绳多五尺；
若将绳四折测之，绳多一尺.
绳长、井深各几何？
(1)“将绳三折测之，绳多五尺”，什么意思？
(2)“若将绳四折测之，绳多一尺”，又是什么意思？
以绳测井
若将绳三折测之，绳多五尺；
若将绳四折测之，绳多一尺.
绳长、井深各几何？
以绳测井
若将绳三折测之，绳多五尺；
若将绳四折测之，绳多一尺.
绳长、井深各几何？
题中有哪些等量关系
用绳子测量水井的深度.如果将绳子折成三等份，绳长比井深多5尺；如果将绳子折成四等份，绳长比井深多1尺.绳长、井深各是多少尺？
关系一
关系二
等量关系
解：设绳长x尺，井深y尺，由题意，得
x
3
x
4
-y=5, ①
-y=1. ②
答：绳长48尺，井深11尺.
解得：
x=48,
y=11.
｛
返回
等量关系
解：设绳长x尺，井深y尺，由题意，得
答：绳长48尺，井深11尺.
3(y+5)=x,
4(y+1)=x.
x=48,
y=11.
解得
返回
比一比：你是智慧之星吗？
古有一捕快，一天晚上他在野外的一个茅屋里，听到外边来了一群人在吵闹，他隐隐约约地听到几个声音，下面有这一古诗为证：
隔壁听到人分银，不知人数不知
银.只知每人五两多六两，每人两
少五两，问你多少人数多少银？
各小组派一名代表回答，评选出智慧之星！
列二元一次方程组解应
用题的步骤是什么？
（1）审题；
（2）设两个未知数，找两个等量关系；
（3）根据等量关系列方程，联立方程组；
（4）解方程组；
（5）检验并作答.
简记为:审.设.找.列.解.验.答
1.设甲数为x，乙数为y，则“甲数的
二倍与乙数的一半的和是15”，列出
方程为____________.
2.小刚有5角硬币和1元硬币各若干
枚，币值共有六元五角，设5角有x
枚，1元有y枚，列出方程为
_____________.
某车间有工人54人，每人平均每天加工 轴杆15个或轴承24个，一个轴杆与两个轴承配成一套.若分配x个工人加工轴杆，y个工人加工轴承，正好使每天加工的产品成套，则可列方程组为（　 ）.
B
x+y=54,
x+y=54,
15x=24y
15x=2×24y
15x=24y
2×15x=24y
15x+24y=54,
x+y=54,
(D)
(A)
(B)
(C)
{
{
{
{
有一群鸽子，其中一部分在树上欢歌，另一部分在地上觅食.树上的一只鸽子对地上觅食的鸽子说：“若从你们中飞上来一只，则树下的鸽子是整个鸽群的三分之一；若从树上飞下去一只，则树上、树下鸽子就一样多了.”你知道树上、树下各有多少只鸽子吗？
《一千零一夜》故事
甲、乙两人赛跑，若乙先跑10米，甲跑5秒即可追上乙；若乙先跑2秒，则甲跑4秒就可追上乙.设甲速为x米/秒，乙速为y米/秒，则可列方程组为(　 ).
B
4y=6x
4x=6y
4y=6x
5y+10=5x,
5x=5y+10,
5x+10=5y,
4x=6y
5y=5x+10,
(A)
(B)
(C)
(D)
{
{
{
{
益智类
生活类
有三块牧场，草长得一样快，面积分别为 公顷，10公顷和24公顷，第一块12头牛可吃4星期，第二块21头可吃9星期,第三块可供多少头牛吃18个星期？
益智类：
返回
解：设牧场每公顷原有草x吨，每周新生草y吨，每头牛每周吃草a吨，第三块可供z头牛吃18个星期，根据题意得：
解得
x=10.8a,
y=0.9a.
答：第三块牧场可供36头牛吃18个星期.
所以24×10.8a+0.9a×24×18=18×za
z=36
{
{
已知某电脑公司有A型，B型，C型三种型号的电脑，其价格分别为A型每台6000元，B型每台4000元，C型每台2500元，我市某中学计划将100500元钱全部用于从该电脑公司购进其中两种不同型号的电脑共36台，请你设计出几种不同的购买方案供该校选择，并说明理由。
生活类：
返回
{
解：设从该电脑公司购进A型电脑x台，B型电脑y台，购
进C型电脑Z台，则可分以下三种情况考虑：
不合题意，应该舍去.
（2）只购进A型电脑和C型电脑，根据题意：
（3）只购进B型电脑和C型电脑，根据题意：
答：有两种方案供校选择，第一种方案是购进A型电脑3台 和C型电脑33台；第二种方案是购进B型电脑7台和C型电脑29台.
（1）只购进A型电脑和B型电脑，根据题意：
解得
{
解得
{
{
解得
{
{
经过本节课的学习，
你有那些学习心得？
完
课本P230问题解决第二题