北师版 数学 七下第三章回顾与思考(共15张)
文档属性
| 名称 | 北师版 数学 七下第三章回顾与思考(共15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 114.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 00:00:00 | ||
图片预览






文档简介
上课准备:课本,练习本,红、黑笔;
上课要求:
(1)回答问题声音洪亮,知道老师提出问题答案的学生把手高高举起示意老师.
(2)小组讨论时,组长负责组织组员活动,每位同学都要积极参与讨论.
(3)组长负责记分: A、B、C、D层次的同学每正确回答一个问题,分别记1、2、3、4分.
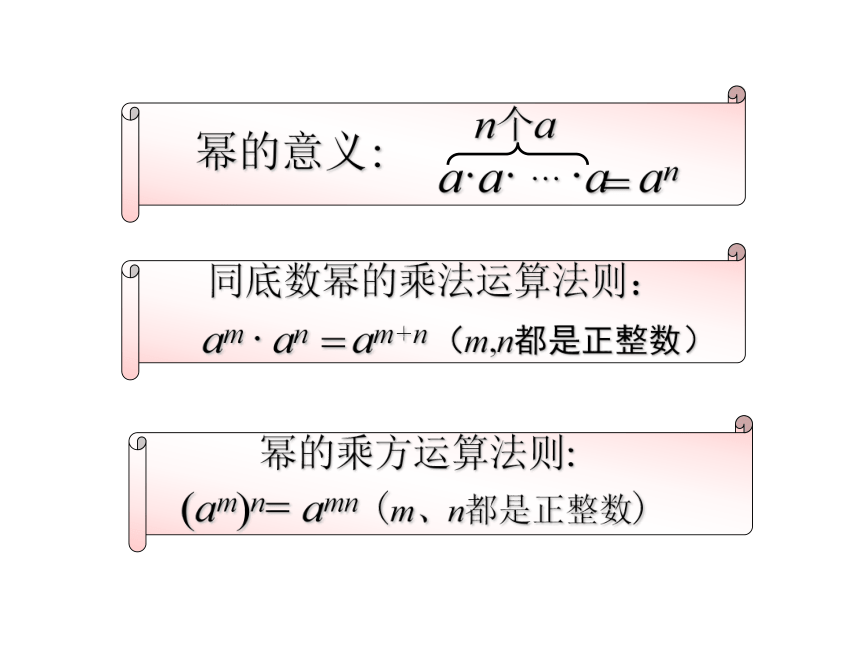
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂的乘法运算法则:
am · an
=
am+n
(m,n都是正整数)
幂的乘方运算法则:
(am)n= (m、n都是正整数)
amn
解:
地球可以近似地看做是球体,如果用V, r 分别代表球的体积和半径,那么 . 地球的半径约为6×103 千米,它的体积大约是多少立方千米?
=
×(6×103)3
=
×
63×109
激趣导入 提出问题
1.2 幂的乘方与积的乘方
第一章 整式的乘除
学习目标
1.掌握幂的乘方与积的乘方的运算性质.
2.运用幂的乘方与积的乘方的运算性质解决一些实际问题.
自主合作 解决问题
独学:自学课本P7:
1.完成做一做,如果m,n都是正整数,那么(ab)n 等于什么?你能说明理由吗?
2.计算:
(1)(3x)2 ; (2)(-2b)5 ;
(3)(-2xy)4 ; (4)(3a2)n .
自学指导:
2.交流:
(1)组长组织组内统一答案,交流方法,
解决疑惑;
(2)组织好语言,老师随机找同学汇报.
(时间3分钟)
自主合作 解决问题
(ab)n = ab·ab·……·ab ( )
=(a·a·……·a) (b·b·……·b) ( )
=an·bn. ( )
幂的意义
乘法交换律、结合律
幂的意义
n个ab
n个a
n个b
展示汇报 反馈点拨
语言叙述:积的乘方=
积的乘方
乘方的积
(ab)n =
an·bn
(m,n都是正整数)
每个因数分别乘方后的积
积的乘方的运算法则
展示汇报 反馈点拨
例2:计算:
(1)(3x)2 ; (2)(-2b)5 ;
(3)(-2xy)4 ; (4)(3a2)n .
=32x2
= 9x2 ;
(1) (3x)2
解:
(2) (-2b)5
= (-2)5b5
= -32b5 ;
(3) (-2xy)4
= (-2x)4 y4
= (-2)4 x4 y4
(4) (3a2)n
= 3n (a2)n
= 3n a2n .
=16x4 y4 ;
展示汇报 反馈点拨
试用简便方法计算:
(ab)n = an·bn
(m,n都是正整数)
逆运用:
an·bn = (ab)n
(1) 23×53
(2) 28×58
(3) (-5)16 × (-2)15
(4) 24 × 44 ×(-0.125)4
= (2×5)3
= 103
= (2×5)8
= 108
= (-5)×[(-5)×(-2)]15
= -5×1015
= [2×4×(-0.125)]4
= 14
= 1 .
展示汇报 反馈点拨
巩固训练 拓展提高
1、计算:
(1) (- 3n)3 ; (2) (5xy)3 ; (3) –a3 +(–4a)2 a .
1、填空:
2、选择: 可以写成_____
A、 B、 C、 D、
3、填空:如果 ,那么 .
4、计算:?
课堂小结 当堂达标
本节课,你有哪些收获?
1、?不用计算器,你能很快求出下列各式的结果吗?
2、若n是正整数,且 ,求 的值.
课堂小结 当堂达标
上课要求:
(1)回答问题声音洪亮,知道老师提出问题答案的学生把手高高举起示意老师.
(2)小组讨论时,组长负责组织组员活动,每位同学都要积极参与讨论.
(3)组长负责记分: A、B、C、D层次的同学每正确回答一个问题,分别记1、2、3、4分.
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂的乘法运算法则:
am · an
=
am+n
(m,n都是正整数)
幂的乘方运算法则:
(am)n= (m、n都是正整数)
amn
解:
地球可以近似地看做是球体,如果用V, r 分别代表球的体积和半径,那么 . 地球的半径约为6×103 千米,它的体积大约是多少立方千米?
=
×(6×103)3
=
×
63×109
激趣导入 提出问题
1.2 幂的乘方与积的乘方
第一章 整式的乘除
学习目标
1.掌握幂的乘方与积的乘方的运算性质.
2.运用幂的乘方与积的乘方的运算性质解决一些实际问题.
自主合作 解决问题
独学:自学课本P7:
1.完成做一做,如果m,n都是正整数,那么(ab)n 等于什么?你能说明理由吗?
2.计算:
(1)(3x)2 ; (2)(-2b)5 ;
(3)(-2xy)4 ; (4)(3a2)n .
自学指导:
2.交流:
(1)组长组织组内统一答案,交流方法,
解决疑惑;
(2)组织好语言,老师随机找同学汇报.
(时间3分钟)
自主合作 解决问题
(ab)n = ab·ab·……·ab ( )
=(a·a·……·a) (b·b·……·b) ( )
=an·bn. ( )
幂的意义
乘法交换律、结合律
幂的意义
n个ab
n个a
n个b
展示汇报 反馈点拨
语言叙述:积的乘方=
积的乘方
乘方的积
(ab)n =
an·bn
(m,n都是正整数)
每个因数分别乘方后的积
积的乘方的运算法则
展示汇报 反馈点拨
例2:计算:
(1)(3x)2 ; (2)(-2b)5 ;
(3)(-2xy)4 ; (4)(3a2)n .
=32x2
= 9x2 ;
(1) (3x)2
解:
(2) (-2b)5
= (-2)5b5
= -32b5 ;
(3) (-2xy)4
= (-2x)4 y4
= (-2)4 x4 y4
(4) (3a2)n
= 3n (a2)n
= 3n a2n .
=16x4 y4 ;
展示汇报 反馈点拨
试用简便方法计算:
(ab)n = an·bn
(m,n都是正整数)
逆运用:
an·bn = (ab)n
(1) 23×53
(2) 28×58
(3) (-5)16 × (-2)15
(4) 24 × 44 ×(-0.125)4
= (2×5)3
= 103
= (2×5)8
= 108
= (-5)×[(-5)×(-2)]15
= -5×1015
= [2×4×(-0.125)]4
= 14
= 1 .
展示汇报 反馈点拨
巩固训练 拓展提高
1、计算:
(1) (- 3n)3 ; (2) (5xy)3 ; (3) –a3 +(–4a)2 a .
1、填空:
2、选择: 可以写成_____
A、 B、 C、 D、
3、填空:如果 ,那么 .
4、计算:?
课堂小结 当堂达标
本节课,你有哪些收获?
1、?不用计算器,你能很快求出下列各式的结果吗?
2、若n是正整数,且 ,求 的值.
课堂小结 当堂达标
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
