宁夏银川三沙源上游学校2020-2021学年高一上学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 宁夏银川三沙源上游学校2020-2021学年高一上学期期末考试数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 14:05:51 | ||
图片预览




文档简介
银川三沙源上游学校2023届高一上学期期末考试
数学试题
一?选择题:本题共12小题,每小题5分,共60分在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,或,则=( )
A. B.
C. 或 D.
2. 函数定义域为( )
A. B. C. D.
3. 如图,是水平放置的的直观图,则的面积为( )
A. 6 B. 32 C. 12 D. 62
4. 设偶函数的定义域为,当时,是增函数,则,,的大小关系是( )
A. B.
C. D.
5. 已知函数,在下列区间中,包含零点的区间是( )
A. B. C. D.
6. 函数的单调递减区间为( )
A. B. C. D.
7. 已知函数(且),则在区间上的最大值为( )
A. B. 或 C. 1 D. ,
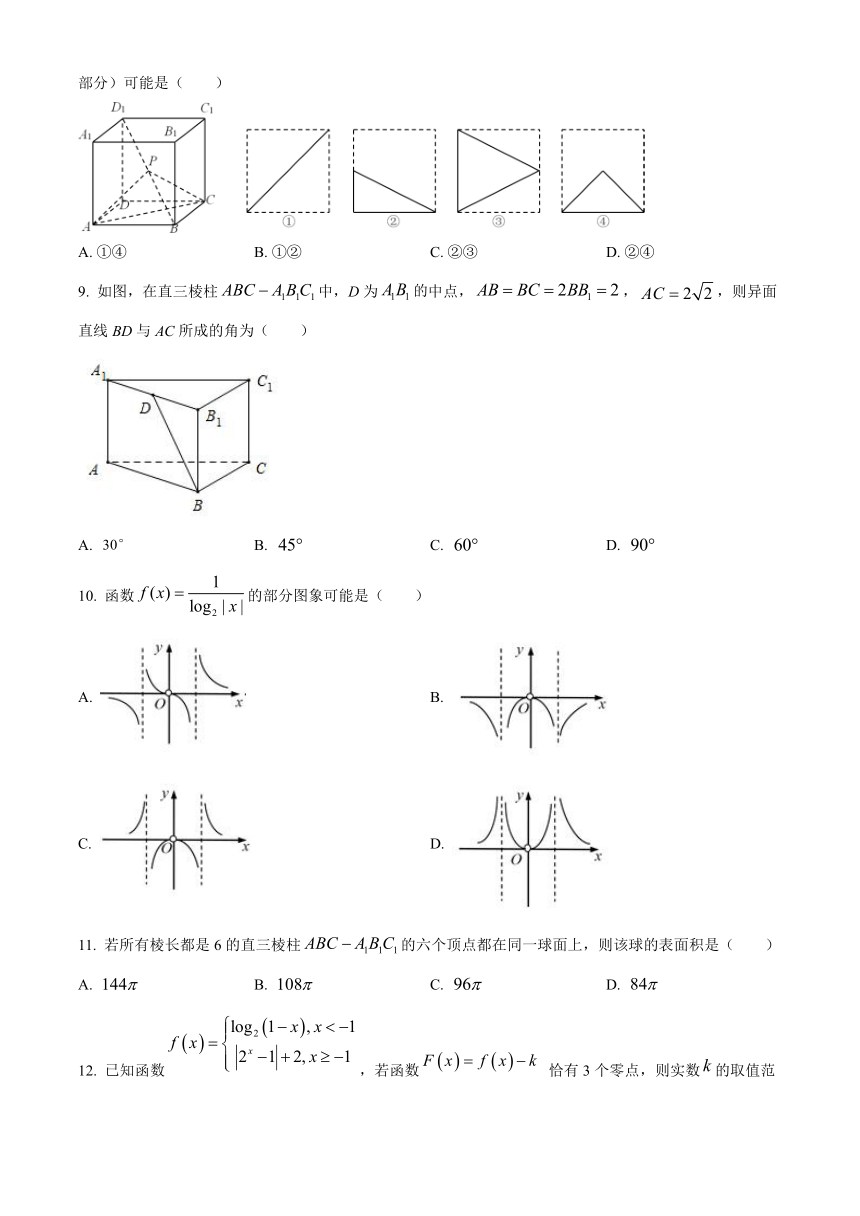
8. 如图,在正方体中,P为的中点,则在该正方体各个面上的正投影(实线部分)可能是( )
A. ①④ B. ①② C. ②③ D. ②④
9. 如图,在直三棱柱中,D为中点,,,则异面直线BD与AC所成的角为( )
A. B. C. D.
10. 函数的部分图象可能是( )
A. B.
C. D.
11. 若所有棱长都是6的直三棱柱的六个顶点都在同一球面上,则该球的表面积是( )
A. B. C. D.
12. 已知函数,若函数 恰有3个零点,则实数的取值范
围是( )
A. B. C. D.
二?填空题:本题共4小题,每小题5分,共20分
13. 圆柱底面半径为3,侧面积为,则圆柱的体积为________.
14. 某几何体的三视图如图所示,则该几何体的表面积为__________.
15. 已知函数,若的最小值是a,则a的值为__________.
16. 大西洋鲑鱼每年都要逆流而上游回产地产卵.研究鲑鱼的科学家发现鲑鱼的游速v(单位:)可以表示为,其中O表示鱼的耗氧量的单位数.当一条鱼的耗氧量是2700个单位时,它的游速是,则a=__________;当这条鱼静止时耗氧量的单位数为__________.
三?解答题:共70分.解答应写出文字说明?证明过程或演算步骤
17. 已知函数是定义域为R的奇函数,当时,.
(1)在坐标系中画出函数在R上完整图象;
(2)求函数在R上解析式.
18. 如图,圆锥的底面直径和高均是4,过的中点作平行于底面的截面,以该截面为底面挖去一个圆柱.
(1)求该圆锥的表面积;
(2)求剩余几何体的体积.
19. 已知函数.
(1)当时,求的单调区间;
(2)当函数的定义域为时,函数的最小值记为,求.
(3)在(2)的条件下,函数的最小值为,求此时a的值.
20. 如图:在正方体中,E为的中点.
(1)求证:平面;
(2)若F为的中点,求证:平面平面.
21. 已知幂函数在上单调递增,又函数.
(1)求实数的值,并说明函数的单调性;
(2)若不等式恒成立,求实数的取值范围.
22. 已知定义域为R的函数和,其中是奇函数,是偶函数,且.
(1)求函数和的解析式;
(2)解不等式:;
(3)若关于x的方程有实根,求正实数的取值范围.
银川三沙源上游学校2023届高一上学期期末考试
数学试题(答案)
一?选择题:本题共12小题,每小题5分,共60分在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,或,则=( )
A. B.
C. 或 D.
【答案】B
2. 函数定义域为( )
A. B. C. D.
【答案】D
3. 如图,是水平放置的的直观图,则的面积为( )
A. 6 B. 32 C. 12 D. 62
【答案】C
4. 设偶函数的定义域为,当时,是增函数,则,,的大小关系是( )
A. B.
C. D.
【答案】B
5. 已知函数,在下列区间中,包含零点的区间是( )
A. B. C. D.
【答案】C
6. 函数的单调递减区间为( )
A. B. C. D.
【答案】B
7. 已知函数(且),则在区间上的最大值为( )
A. B. 或 C. 1 D. ,
【答案】B
8. 如图,在正方体中,P为的中点,则在该正方体各个面上的正投影(实线部分)可能是( )
A. ①④ B. ①② C. ②③ D. ②④
【答案】A
9. 如图,在直三棱柱中,D为中点,,,则异面直线BD与AC所成的角为( )
A. B. C. D.
【答案】C
10. 函数的部分图象可能是( )
A. B.
C. D.
【答案】C
11. 若所有棱长都是6的直三棱柱的六个顶点都在同一球面上,则该球的表面积是( )
A. B. C. D.
【答案】D
12. 已知函数,若函数 恰有3个零点,则实数的取值范围是( )
A. B. C. D.
【答案】A
二?填空题:本题共4小题,每小题5分,共20分
13. 圆柱底面半径为3,侧面积为,则圆柱的体积为________.
【答案】
14. 某几何体的三视图如图所示,则该几何体的表面积为__________.
【答案】
15. 已知函数,若的最小值是a,则a的值为__________.
【答案】
16. 大西洋鲑鱼每年都要逆流而上游回产地产卵.研究鲑鱼的科学家发现鲑鱼的游速v(单位:)可以表示为,其中O表示鱼的耗氧量的单位数.当一条鱼的耗氧量是2700个单位时,它的游速是,则a=__________;当这条鱼静止时耗氧量的单位数为__________.
【答案】 (1). (2). 100
三?解答题:共70分.解答应写出文字说明?证明过程或演算步骤
17. 已知函数是定义域为R的奇函数,当时,.
(1)在坐标系中画出函数在R上完整图象;
(2)求函数在R上解析式.
【答案】(1)图象答案见解析;(2).
18. 如图,圆锥的底面直径和高均是4,过的中点作平行于底面的截面,以该截面为底面挖去一个圆柱.
(1)求该圆锥的表面积;
(2)求剩余几何体的体积.
【答案】(1);(2).
19. 已知函数.
(1)当时,求的单调区间;
(2)当函数的定义域为时,函数的最小值记为,求.
(3)在(2)的条件下,函数的最小值为,求此时a的值.
【答案】(1)在上单调递减,在上单调递增;(2);(3).
20. 如图:在正方体中,E为的中点.
(1)求证:平面;
(2)若F为的中点,求证:平面平面.
【答案】(1)证明见解析;(2)证明见解析.
21. 已知幂函数在上单调递增,又函数.
(1)求实数的值,并说明函数的单调性;
(2)若不等式恒成立,求实数的取值范围.
【答案】(1)见解析;(2)
22. 已知定义域为R的函数和,其中是奇函数,是偶函数,且.
(1)求函数和的解析式;
(2)解不等式:;
(3)若关于x的方程有实根,求正实数的取值范围.
【答案】(1),(2)(3)
数学试题
一?选择题:本题共12小题,每小题5分,共60分在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,或,则=( )
A. B.
C. 或 D.
2. 函数定义域为( )
A. B. C. D.
3. 如图,是水平放置的的直观图,则的面积为( )
A. 6 B. 32 C. 12 D. 62
4. 设偶函数的定义域为,当时,是增函数,则,,的大小关系是( )
A. B.
C. D.
5. 已知函数,在下列区间中,包含零点的区间是( )
A. B. C. D.
6. 函数的单调递减区间为( )
A. B. C. D.
7. 已知函数(且),则在区间上的最大值为( )
A. B. 或 C. 1 D. ,
8. 如图,在正方体中,P为的中点,则在该正方体各个面上的正投影(实线部分)可能是( )
A. ①④ B. ①② C. ②③ D. ②④
9. 如图,在直三棱柱中,D为中点,,,则异面直线BD与AC所成的角为( )
A. B. C. D.
10. 函数的部分图象可能是( )
A. B.
C. D.
11. 若所有棱长都是6的直三棱柱的六个顶点都在同一球面上,则该球的表面积是( )
A. B. C. D.
12. 已知函数,若函数 恰有3个零点,则实数的取值范
围是( )
A. B. C. D.
二?填空题:本题共4小题,每小题5分,共20分
13. 圆柱底面半径为3,侧面积为,则圆柱的体积为________.
14. 某几何体的三视图如图所示,则该几何体的表面积为__________.
15. 已知函数,若的最小值是a,则a的值为__________.
16. 大西洋鲑鱼每年都要逆流而上游回产地产卵.研究鲑鱼的科学家发现鲑鱼的游速v(单位:)可以表示为,其中O表示鱼的耗氧量的单位数.当一条鱼的耗氧量是2700个单位时,它的游速是,则a=__________;当这条鱼静止时耗氧量的单位数为__________.
三?解答题:共70分.解答应写出文字说明?证明过程或演算步骤
17. 已知函数是定义域为R的奇函数,当时,.
(1)在坐标系中画出函数在R上完整图象;
(2)求函数在R上解析式.
18. 如图,圆锥的底面直径和高均是4,过的中点作平行于底面的截面,以该截面为底面挖去一个圆柱.
(1)求该圆锥的表面积;
(2)求剩余几何体的体积.
19. 已知函数.
(1)当时,求的单调区间;
(2)当函数的定义域为时,函数的最小值记为,求.
(3)在(2)的条件下,函数的最小值为,求此时a的值.
20. 如图:在正方体中,E为的中点.
(1)求证:平面;
(2)若F为的中点,求证:平面平面.
21. 已知幂函数在上单调递增,又函数.
(1)求实数的值,并说明函数的单调性;
(2)若不等式恒成立,求实数的取值范围.
22. 已知定义域为R的函数和,其中是奇函数,是偶函数,且.
(1)求函数和的解析式;
(2)解不等式:;
(3)若关于x的方程有实根,求正实数的取值范围.
银川三沙源上游学校2023届高一上学期期末考试
数学试题(答案)
一?选择题:本题共12小题,每小题5分,共60分在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,或,则=( )
A. B.
C. 或 D.
【答案】B
2. 函数定义域为( )
A. B. C. D.
【答案】D
3. 如图,是水平放置的的直观图,则的面积为( )
A. 6 B. 32 C. 12 D. 62
【答案】C
4. 设偶函数的定义域为,当时,是增函数,则,,的大小关系是( )
A. B.
C. D.
【答案】B
5. 已知函数,在下列区间中,包含零点的区间是( )
A. B. C. D.
【答案】C
6. 函数的单调递减区间为( )
A. B. C. D.
【答案】B
7. 已知函数(且),则在区间上的最大值为( )
A. B. 或 C. 1 D. ,
【答案】B
8. 如图,在正方体中,P为的中点,则在该正方体各个面上的正投影(实线部分)可能是( )
A. ①④ B. ①② C. ②③ D. ②④
【答案】A
9. 如图,在直三棱柱中,D为中点,,,则异面直线BD与AC所成的角为( )
A. B. C. D.
【答案】C
10. 函数的部分图象可能是( )
A. B.
C. D.
【答案】C
11. 若所有棱长都是6的直三棱柱的六个顶点都在同一球面上,则该球的表面积是( )
A. B. C. D.
【答案】D
12. 已知函数,若函数 恰有3个零点,则实数的取值范围是( )
A. B. C. D.
【答案】A
二?填空题:本题共4小题,每小题5分,共20分
13. 圆柱底面半径为3,侧面积为,则圆柱的体积为________.
【答案】
14. 某几何体的三视图如图所示,则该几何体的表面积为__________.
【答案】
15. 已知函数,若的最小值是a,则a的值为__________.
【答案】
16. 大西洋鲑鱼每年都要逆流而上游回产地产卵.研究鲑鱼的科学家发现鲑鱼的游速v(单位:)可以表示为,其中O表示鱼的耗氧量的单位数.当一条鱼的耗氧量是2700个单位时,它的游速是,则a=__________;当这条鱼静止时耗氧量的单位数为__________.
【答案】 (1). (2). 100
三?解答题:共70分.解答应写出文字说明?证明过程或演算步骤
17. 已知函数是定义域为R的奇函数,当时,.
(1)在坐标系中画出函数在R上完整图象;
(2)求函数在R上解析式.
【答案】(1)图象答案见解析;(2).
18. 如图,圆锥的底面直径和高均是4,过的中点作平行于底面的截面,以该截面为底面挖去一个圆柱.
(1)求该圆锥的表面积;
(2)求剩余几何体的体积.
【答案】(1);(2).
19. 已知函数.
(1)当时,求的单调区间;
(2)当函数的定义域为时,函数的最小值记为,求.
(3)在(2)的条件下,函数的最小值为,求此时a的值.
【答案】(1)在上单调递减,在上单调递增;(2);(3).
20. 如图:在正方体中,E为的中点.
(1)求证:平面;
(2)若F为的中点,求证:平面平面.
【答案】(1)证明见解析;(2)证明见解析.
21. 已知幂函数在上单调递增,又函数.
(1)求实数的值,并说明函数的单调性;
(2)若不等式恒成立,求实数的取值范围.
【答案】(1)见解析;(2)
22. 已知定义域为R的函数和,其中是奇函数,是偶函数,且.
(1)求函数和的解析式;
(2)解不等式:;
(3)若关于x的方程有实根,求正实数的取值范围.
【答案】(1),(2)(3)
同课章节目录
