2020——2021学年鲁教版(五四制)六年级数学下册《5.1 线段 射线 直线》自主学习同步训练(word版含解析)
文档属性
| 名称 | 2020——2021学年鲁教版(五四制)六年级数学下册《5.1 线段 射线 直线》自主学习同步训练(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 143.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 22:04:30 | ||
图片预览


文档简介
2021年鲁教版六年级数学下册《5.1 线段 射线 直线》自主学习同步训练(附答案)
1.经过A、B两点可以确定几条直线( )
A.1条 B.2条 C.3条 D.无数条
2.木匠在木料上画线,先确定两个点的位置,就能把线画得很准确,其依据是( )
A.两点确定一条直线 B.两点确定一条线段
C.过一点有一条直线 D.过一点有无数条直线
3.在墙壁上固定一根横放的木条,则至少需要钉子的枚数是( )
A.1枚 B.2枚 C.3枚 D.任意枚
4.如图,下列不正确的几何语句是( )
A.直线AB与直线BA是同一条直线 B.射线OA与射线OB是同一条射线
C.射线OA与射线AB是同一条射线 D.线段AB与线段BA是同一条线段
5.下列说法正确的有( )
①过两点只能画一条直线;②过两点只能画一条射线;③过两点只能画一条线段.
A.1个 B.2个 C.3个 D.0个
6.在平面内有A、B、C、D四点,过其中任意两点画直线,则最多可以画( )
A.4条 B.6条 C.8条 D.无数条
7.下列说法正确的是( )
A.延长直线AB到点C B.延长射线AB到点C
C.延长线段AB到点C D.射线AB与射线BA是同一条射线
8.下列语句中,叙述准确规范的是( )
A.直线a,b相交于点m B.延长直线AB
C.线段ab与线段bc交于点b D.延长线段AC至点B,使BC=AC
9.下列说法中错误的是( )
A.线段AB和射线AB都是直线的一部分 B.直线AB和直线BA是同一条直线
C.射线AB和射线BA是同一条射线 D.线段AB和线段BA是同一条线段
10.图中共有线段( )
A.4条 B.6条 C.8条 D.10条
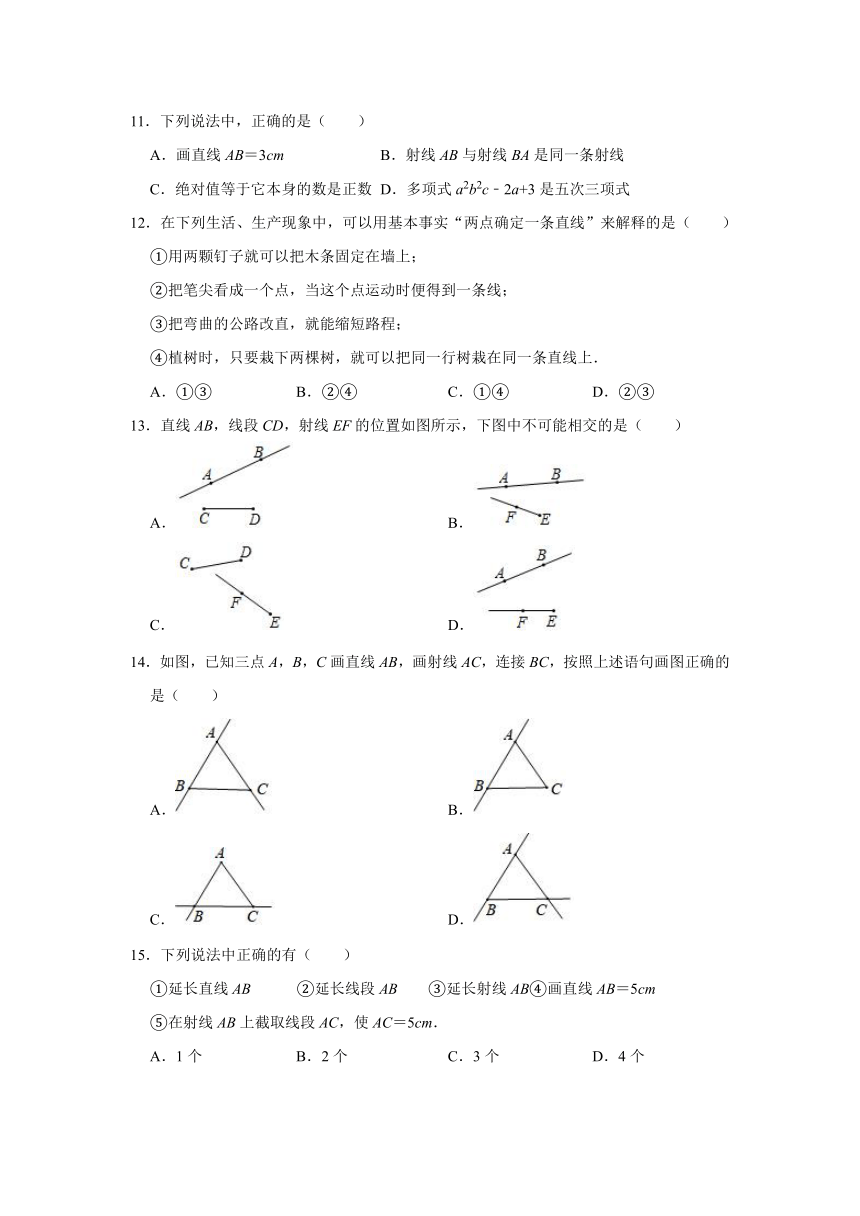
11.下列说法中,正确的是( )
A.画直线AB=3cm B.射线AB与射线BA是同一条射线
C.绝对值等于它本身的数是正数 D.多项式a2b2c﹣2a+3是五次三项式
12.在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的是( )
①用两颗钉子就可以把木条固定在墙上;
②把笔尖看成一个点,当这个点运动时便得到一条线;
③把弯曲的公路改直,就能缩短路程;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上.
A.①③ B.②④ C.①④ D.②③
13.直线AB,线段CD,射线EF的位置如图所示,下图中不可能相交的是( )
A. B.
C. D.
14.如图,已知三点A,B,C画直线AB,画射线AC,连接BC,按照上述语句画图正确的是( )
A. B.
C. D.
15.下列说法中正确的有( )
①延长直线AB ②延长线段AB ③延长射线AB④画直线AB=5cm
⑤在射线AB上截取线段AC,使AC=5cm.
A.1个 B.2个 C.3个 D.4个
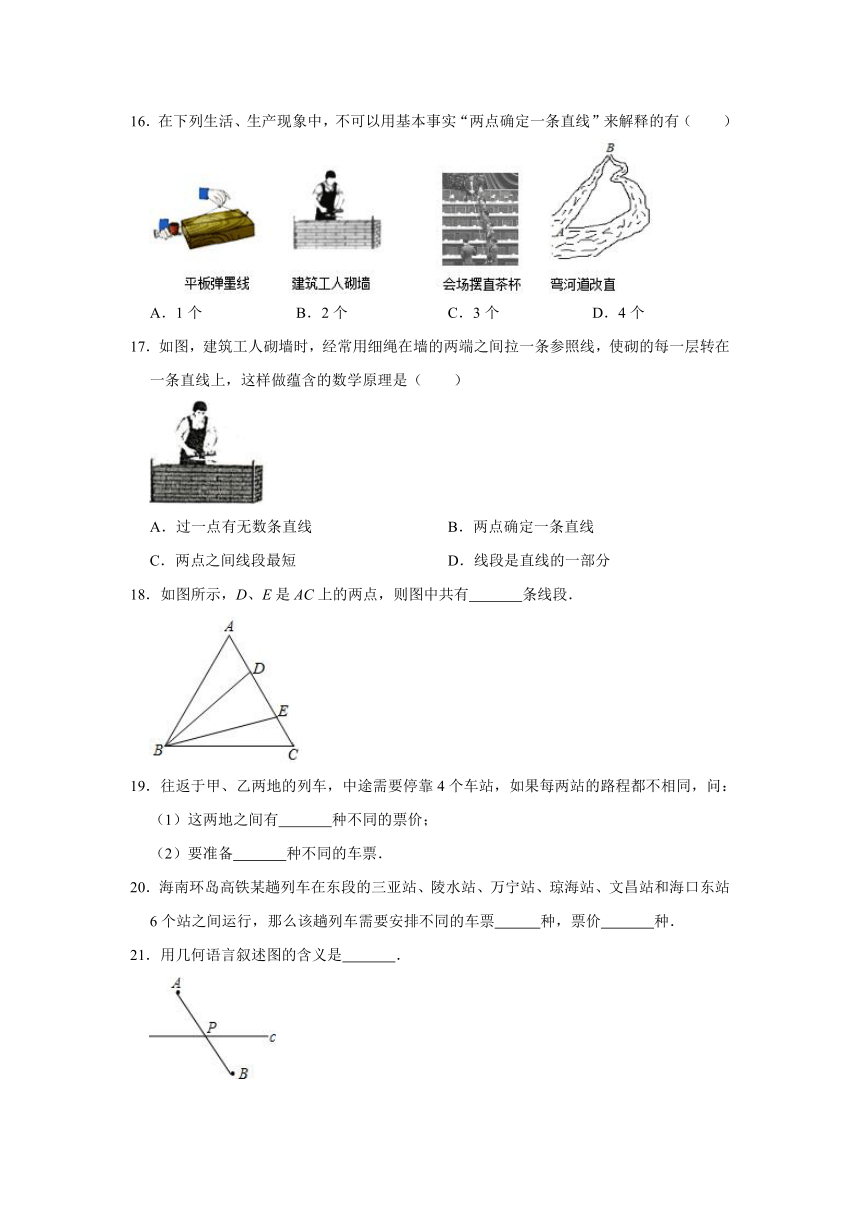
16.在下列生活、生产现象中,不可以用基本事实“两点确定一条直线”来解释的有( )
A.1个 B.2个 C.3个 D.4个
17.如图,建筑工人砌墙时,经常用细绳在墙的两端之间拉一条参照线,使砌的每一层转在一条直线上,这样做蕴含的数学原理是( )
A.过一点有无数条直线 B.两点确定一条直线
C.两点之间线段最短 D.线段是直线的一部分
18.如图所示,D、E是AC上的两点,则图中共有 条线段.
19.往返于甲、乙两地的列车,中途需要停靠4个车站,如果每两站的路程都不相同,问:
(1)这两地之间有 种不同的票价;
(2)要准备 种不同的车票.
20.海南环岛高铁某趟列车在东段的三亚站、陵水站、万宁站、琼海站、文昌站和海口东站6个站之间运行,那么该趟列车需要安排不同的车票 种,票价 种.
21.用几何语言叙述图的含义是 .
22.乘火车从A站出发,沿途经过2个车站方可到达B站,那么A,B两站之间需要安排 种不同的车票.
23.往返于甲、乙两地的客车,中途停靠4个车站(来回票价一样),且任意两站间的票价都不同,共有 种不同的票价,需准备 种车票.
24.要在墙上固定一根木条,至少需要 根钉子,理由是: .
25.作图题:如图,已知平面上四点A,B,C,D.
(1)画直线AD;
(2)画射线BC,与直线AD相交于O;
(3)连结AC,BD相交于点F.
26.如图,平面上有四个点A,B,C,D,根据下列语句画图:
(1)画线段AC、BD交于E点;
(2)作射线BC;
(3)取一点P,使点P既在直线AB上又在直线CD上.
参考答案
1.解:经过A、B两点可以确定1条直线.
故选:A.
2.解:木匠在木料上画线,先确定两个点的位置,就能把线画得很准确,其依据是两点确定一条直线,
故选:A.
3.解:∵两点确定一条直线,
∴至少需要2枚钉子.
故选:B.
4.解:A正确,因为直线向两方无限延伸;
B正确,射线的端点和方向都相同;
C错误,因为射线的端点不相同;
D正确.故选:C.
5.解:①过两点只能画一条直线,故正确;
②过两点可以画2条射线,故错误;
③由于这两点并非一定为线段的端点,过两点可以画无数条线段,故错误.
综上所述,正确的结论有1个.故选:A.
6.解:分三种情况:
1、四点在同一直线上时,只可画1条;
2、当三点在同一直线上,另一点不在这条直线上,可画4条;
3、当没有三点共线时,可画6条.
所以最多可以画6条.故选:B.
7.解:A、直线可以沿两个方向无限延伸,故不能说延长直线AB,故本选项不符合题意;
B、射线可沿延伸方向无限延伸,故不能说延长射线AB,故本选项不符合题意;
C、线段不能延伸,可以说延长线段AB到点C,故本选项符合题意;
D、射线AB与射线BA不是同一条射线,故本选项不符合题意;
故选:C.
8.解:A.点应该用大写字母表示,直线a,b相交于点M,原说法错误,故本选项不符合题意;
B.直线向两端无限延伸,原说法错误,故本选项不符合题意;
C.线段不可以用两个小写字母表示,可以用一个小写字母表示,原说法错误,故本选项不符合题意;
D.可以延长线段AC至点B.使BC=AC,原说法正确,故本选项符合题意;
故选:D.
9.解:A、线段AB和射线AB都是直线的一部分,正确,不合题意;
B、直线AB和直线BA是同一条直线,正确,不符合题意;
C、射线AB和射线BA不是同一条射线,错误,符合题意;
D、线段AB和线段BA是同一条线段,正确,不合题意;
故选:C.
10.解:图中的线段有AC、AD、AE、AB;CD、CE、CB;DE、DB;EB;共10条,
故选:D.
11.解:A.直线可以向两边无限延伸,故“画直线AB=3cm”说法错误;
B.射线AB与射线BA是端点不同的两条射线,故“射线AB与射线BA是同一条射线”说法错误;
C.绝对值等于它本身的数是正数和0,故原说法错误;
D.多项式a2b2c﹣2a+3是五次三项式,正确.
故选:D.
12.解:①用两颗钉子就可以把木条固定在墙上,可以用基本事实“两点确定一条直线”来解释;
②把笔尖看成一个点,当这个点运动时便得到一条线,可以用基本事实“无数个点组成线”来解释;
③把弯曲的公路改直,就能缩短路程,可以用基本事实“两点之间线段最短”来解释;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上,可以用基本事实“两点确定一条直线”来解释.
故选:C.
13.解:A选项中,直线AB与线段CD无交点,符合题意;
B选项中,直线AB与射线EF有交点,不合题意;
C选项中,线段CD与射线EF有交点,不合题意;
D选项中,直线AB与射线EF有交点,不合题意;
故选:A.
14.解:画直线AB,画射线AC,连接BC,如图所示:
故选:A.
15.解:①延长直线AB,说法错误;
②延长线段AB,说法正确;
③延长射线AB,说法错误;
④画直线AB=5cm,说法错误;
⑤在射线AB上截取线段AC,使AC=5cm,说法正确;
∴正确的个数为2个.
故选:B.
16.解:第一、二、三幅图中的生活、生产现象可以用基本事实“两点确定一条直线”来解释,第四幅图中利用的是“两点之间,线段最短”的知识.
故选:A.
17.解:建筑工人砌墙时,经常用细绳在墙的两端之间拉一条参照线,使砌的每一层转在一条直线上,
这种做法用几何知识解释应是:两点确定一条直线.故选:B.
18.解:图中的线段有:AD,AE,AC,DE,DC,EC,BA,BD,BE,BC,共10条.
故答案为:10.
19.解:(1)如图:
根据线段的定义:可知图中共有线段有AC,AD,AE,AF,AB,CD、CE,CF、CB、DE,DF、DB、EF,EB,FB共15条,有15种不同的票价;
(2)因车票需要考虑方向性,如,“A→C”与“C→A”票价相同,但车票不同,故需要准备30种车票.
故答案为:15;30.
20.解:令6个站分别为A、B、C、D、E、F,
则可得所组成的线段有15条,即需要安排15×2=30种不同的车票.
故答案为:30、15.
21.解:图中有线段AB,直线c,它们相交于点P;故应填:线段AB和直线c相交于点P.
22.解:
从A到B共有AC、AD、AB、CD、CB、DB共6条,
因为从两站出发点不同,车票就不同如A到C与C到A不同,故应有12种,
故答案为:12
23.解:根据线段的定义:可知图中共有线段有AC,AD,AE,AF,AB,CD、CE,CF、CB、DE,DF、DB、EF,EB,FB共15条,有15种不同的票价;
因车票需要考虑方向性,如,“A→C”与“C→A”票价相同,但车票不同,故需要准备30种车票.
故答案为:15;30.
24.解:根据直线的性质,要在墙上固定一根木条,至少需要两根钉子,理由是:两点确定一条直线.
25.解:(1)(2)(3)如图所示:
26.解:(1)如图所示:
;
(2)如图所示,
(3)如图所示,
.
1.经过A、B两点可以确定几条直线( )
A.1条 B.2条 C.3条 D.无数条
2.木匠在木料上画线,先确定两个点的位置,就能把线画得很准确,其依据是( )
A.两点确定一条直线 B.两点确定一条线段
C.过一点有一条直线 D.过一点有无数条直线
3.在墙壁上固定一根横放的木条,则至少需要钉子的枚数是( )
A.1枚 B.2枚 C.3枚 D.任意枚
4.如图,下列不正确的几何语句是( )
A.直线AB与直线BA是同一条直线 B.射线OA与射线OB是同一条射线
C.射线OA与射线AB是同一条射线 D.线段AB与线段BA是同一条线段
5.下列说法正确的有( )
①过两点只能画一条直线;②过两点只能画一条射线;③过两点只能画一条线段.
A.1个 B.2个 C.3个 D.0个
6.在平面内有A、B、C、D四点,过其中任意两点画直线,则最多可以画( )
A.4条 B.6条 C.8条 D.无数条
7.下列说法正确的是( )
A.延长直线AB到点C B.延长射线AB到点C
C.延长线段AB到点C D.射线AB与射线BA是同一条射线
8.下列语句中,叙述准确规范的是( )
A.直线a,b相交于点m B.延长直线AB
C.线段ab与线段bc交于点b D.延长线段AC至点B,使BC=AC
9.下列说法中错误的是( )
A.线段AB和射线AB都是直线的一部分 B.直线AB和直线BA是同一条直线
C.射线AB和射线BA是同一条射线 D.线段AB和线段BA是同一条线段
10.图中共有线段( )
A.4条 B.6条 C.8条 D.10条
11.下列说法中,正确的是( )
A.画直线AB=3cm B.射线AB与射线BA是同一条射线
C.绝对值等于它本身的数是正数 D.多项式a2b2c﹣2a+3是五次三项式
12.在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的是( )
①用两颗钉子就可以把木条固定在墙上;
②把笔尖看成一个点,当这个点运动时便得到一条线;
③把弯曲的公路改直,就能缩短路程;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上.
A.①③ B.②④ C.①④ D.②③
13.直线AB,线段CD,射线EF的位置如图所示,下图中不可能相交的是( )
A. B.
C. D.
14.如图,已知三点A,B,C画直线AB,画射线AC,连接BC,按照上述语句画图正确的是( )
A. B.
C. D.
15.下列说法中正确的有( )
①延长直线AB ②延长线段AB ③延长射线AB④画直线AB=5cm
⑤在射线AB上截取线段AC,使AC=5cm.
A.1个 B.2个 C.3个 D.4个
16.在下列生活、生产现象中,不可以用基本事实“两点确定一条直线”来解释的有( )
A.1个 B.2个 C.3个 D.4个
17.如图,建筑工人砌墙时,经常用细绳在墙的两端之间拉一条参照线,使砌的每一层转在一条直线上,这样做蕴含的数学原理是( )
A.过一点有无数条直线 B.两点确定一条直线
C.两点之间线段最短 D.线段是直线的一部分
18.如图所示,D、E是AC上的两点,则图中共有 条线段.
19.往返于甲、乙两地的列车,中途需要停靠4个车站,如果每两站的路程都不相同,问:
(1)这两地之间有 种不同的票价;
(2)要准备 种不同的车票.
20.海南环岛高铁某趟列车在东段的三亚站、陵水站、万宁站、琼海站、文昌站和海口东站6个站之间运行,那么该趟列车需要安排不同的车票 种,票价 种.
21.用几何语言叙述图的含义是 .
22.乘火车从A站出发,沿途经过2个车站方可到达B站,那么A,B两站之间需要安排 种不同的车票.
23.往返于甲、乙两地的客车,中途停靠4个车站(来回票价一样),且任意两站间的票价都不同,共有 种不同的票价,需准备 种车票.
24.要在墙上固定一根木条,至少需要 根钉子,理由是: .
25.作图题:如图,已知平面上四点A,B,C,D.
(1)画直线AD;
(2)画射线BC,与直线AD相交于O;
(3)连结AC,BD相交于点F.
26.如图,平面上有四个点A,B,C,D,根据下列语句画图:
(1)画线段AC、BD交于E点;
(2)作射线BC;
(3)取一点P,使点P既在直线AB上又在直线CD上.
参考答案
1.解:经过A、B两点可以确定1条直线.
故选:A.
2.解:木匠在木料上画线,先确定两个点的位置,就能把线画得很准确,其依据是两点确定一条直线,
故选:A.
3.解:∵两点确定一条直线,
∴至少需要2枚钉子.
故选:B.
4.解:A正确,因为直线向两方无限延伸;
B正确,射线的端点和方向都相同;
C错误,因为射线的端点不相同;
D正确.故选:C.
5.解:①过两点只能画一条直线,故正确;
②过两点可以画2条射线,故错误;
③由于这两点并非一定为线段的端点,过两点可以画无数条线段,故错误.
综上所述,正确的结论有1个.故选:A.
6.解:分三种情况:
1、四点在同一直线上时,只可画1条;
2、当三点在同一直线上,另一点不在这条直线上,可画4条;
3、当没有三点共线时,可画6条.
所以最多可以画6条.故选:B.
7.解:A、直线可以沿两个方向无限延伸,故不能说延长直线AB,故本选项不符合题意;
B、射线可沿延伸方向无限延伸,故不能说延长射线AB,故本选项不符合题意;
C、线段不能延伸,可以说延长线段AB到点C,故本选项符合题意;
D、射线AB与射线BA不是同一条射线,故本选项不符合题意;
故选:C.
8.解:A.点应该用大写字母表示,直线a,b相交于点M,原说法错误,故本选项不符合题意;
B.直线向两端无限延伸,原说法错误,故本选项不符合题意;
C.线段不可以用两个小写字母表示,可以用一个小写字母表示,原说法错误,故本选项不符合题意;
D.可以延长线段AC至点B.使BC=AC,原说法正确,故本选项符合题意;
故选:D.
9.解:A、线段AB和射线AB都是直线的一部分,正确,不合题意;
B、直线AB和直线BA是同一条直线,正确,不符合题意;
C、射线AB和射线BA不是同一条射线,错误,符合题意;
D、线段AB和线段BA是同一条线段,正确,不合题意;
故选:C.
10.解:图中的线段有AC、AD、AE、AB;CD、CE、CB;DE、DB;EB;共10条,
故选:D.
11.解:A.直线可以向两边无限延伸,故“画直线AB=3cm”说法错误;
B.射线AB与射线BA是端点不同的两条射线,故“射线AB与射线BA是同一条射线”说法错误;
C.绝对值等于它本身的数是正数和0,故原说法错误;
D.多项式a2b2c﹣2a+3是五次三项式,正确.
故选:D.
12.解:①用两颗钉子就可以把木条固定在墙上,可以用基本事实“两点确定一条直线”来解释;
②把笔尖看成一个点,当这个点运动时便得到一条线,可以用基本事实“无数个点组成线”来解释;
③把弯曲的公路改直,就能缩短路程,可以用基本事实“两点之间线段最短”来解释;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上,可以用基本事实“两点确定一条直线”来解释.
故选:C.
13.解:A选项中,直线AB与线段CD无交点,符合题意;
B选项中,直线AB与射线EF有交点,不合题意;
C选项中,线段CD与射线EF有交点,不合题意;
D选项中,直线AB与射线EF有交点,不合题意;
故选:A.
14.解:画直线AB,画射线AC,连接BC,如图所示:
故选:A.
15.解:①延长直线AB,说法错误;
②延长线段AB,说法正确;
③延长射线AB,说法错误;
④画直线AB=5cm,说法错误;
⑤在射线AB上截取线段AC,使AC=5cm,说法正确;
∴正确的个数为2个.
故选:B.
16.解:第一、二、三幅图中的生活、生产现象可以用基本事实“两点确定一条直线”来解释,第四幅图中利用的是“两点之间,线段最短”的知识.
故选:A.
17.解:建筑工人砌墙时,经常用细绳在墙的两端之间拉一条参照线,使砌的每一层转在一条直线上,
这种做法用几何知识解释应是:两点确定一条直线.故选:B.
18.解:图中的线段有:AD,AE,AC,DE,DC,EC,BA,BD,BE,BC,共10条.
故答案为:10.
19.解:(1)如图:
根据线段的定义:可知图中共有线段有AC,AD,AE,AF,AB,CD、CE,CF、CB、DE,DF、DB、EF,EB,FB共15条,有15种不同的票价;
(2)因车票需要考虑方向性,如,“A→C”与“C→A”票价相同,但车票不同,故需要准备30种车票.
故答案为:15;30.
20.解:令6个站分别为A、B、C、D、E、F,
则可得所组成的线段有15条,即需要安排15×2=30种不同的车票.
故答案为:30、15.
21.解:图中有线段AB,直线c,它们相交于点P;故应填:线段AB和直线c相交于点P.
22.解:
从A到B共有AC、AD、AB、CD、CB、DB共6条,
因为从两站出发点不同,车票就不同如A到C与C到A不同,故应有12种,
故答案为:12
23.解:根据线段的定义:可知图中共有线段有AC,AD,AE,AF,AB,CD、CE,CF、CB、DE,DF、DB、EF,EB,FB共15条,有15种不同的票价;
因车票需要考虑方向性,如,“A→C”与“C→A”票价相同,但车票不同,故需要准备30种车票.
故答案为:15;30.
24.解:根据直线的性质,要在墙上固定一根木条,至少需要两根钉子,理由是:两点确定一条直线.
25.解:(1)(2)(3)如图所示:
26.解:(1)如图所示:
;
(2)如图所示,
(3)如图所示,
.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
