2020-2021学年人教版数学七年级下册 第七章7.1.1----7.1.2同步能力测试题(word版含答案)
文档属性
| 名称 | 2020-2021学年人教版数学七年级下册 第七章7.1.1----7.1.2同步能力测试题(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 378.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 22:04:21 | ||
图片预览




文档简介
7.1.1《有序数对》
一、选择题
1.下面的有序数对的写法正确的是( )
A.(1、3) B.(1,3) C.1,3 D.以上表达都正确
2.我们用以下表格来表示某超市的平面示意图.如果用(C,3)表示“体育用品”的位置,那么表示“儿童服装”的位置应记作( )
A.(A,3) B.(B,4) C.(C,2) D.(D,1)
3.体育课上,七年级某班49名同学在操场上练习正方形方队,他们站成7×7方队,每横队7人,每纵队7人,小敏在第2纵队的排头,记为(1,2),小娟在第5纵队的队尾,则小娟的位置应记为( )
A.(6,5) B.(5,6) C.(5,7) D.(7,5)
4.观察下表,若用有序实数对(m,n)表示第m行第n列的数,如:(4,3)表示实数6,则(20,18)表示的数是(???)
A.18???????? B.20?????? C.37 ??????D.38
5.下列关于有序数对的说法正确的是(?? )
A.(3,4)与(4,3)表示的位置相同
B.(a,b)与(b,a)表示的位置肯定不同
C.(3,5)与(5,3)是表示不同位置的两个有序数对
D.有序数对(2,2)与(2,2)表示两个不同的位置
6.七年级⑴班的座位共有6排8列,张军同学的座位在2排3列,我们可以记作(2,3),那么吴灏同学的座位在5排6列,应记作(?? )
A.(5,6)??? B.(6,5)?? ? C.(6,8)??? D.(3,2)
7.将正整数按如下图所示的规律排列,若用有序数对(m,n)表示从上到下第m行,和该行从左到右第n个数,如(4,2)表示整数8,则(8,4)表示的整数是( )
A.31 B.32 C.33 D.41
8.观察下列数对:(1,1) , (1,2) , (2,1) , (1,3) , (2,2) , (3,1) , (1,4) , (2,3) , (3,2) , (4,1) , (1,5) , (2,4)...那么第32个数对是( )
A.(4,4) B.(4,5) C.(4,6) D.(5,4)
9.如下图所示,图中是沈阳市地图简图的一部分,图中“故宫”、“鼓楼”所在的区域分别是( )
A.D7,E6 B.D6,E7 C.E7,D6 D.E6,D7
10.如下表所示,小聪家在A点,用(3,1)表示,小明家在B点,用(8,5)表示.若用(3,1)-(4,1)-(5,1)-(5,2)-(5,3)-(5,4)-(6,4)-(7,4)表示由A到B的一种走法,并规定从A到B只能向下或向右走.那么下面走法符合题意的有( )
A.(3,1)-(4,1)-(4,2)-(5,2)-(6,2)-(7,2)-(7,3)-(8,3)
B.(3,1)-(4,1)-(5,1)-(6,1)-(7,1)-(7,2)-(7,3)-(7,4)
C.(3,1)-(4,1)-(5,1)-(6,1)-(7,1)-(8,1)-(8,2)-(8,3)-(8,4)-(7,4)
D.(3,1)-(4,1)-(5,1)-(6,1)-(6,2)-(6,3)-(6,4)-(6,5)-(7,5)-(7,4)
二、填空题
11.下列说法中:①座位是4排2号;②某城市在东经118°,北纬29°;③某校在昌荣大道229号;④甲地距乙地2 km,其中能确定位置的有________个.
12.如果用(7,3)表示七年级三班,则(9,6)表示____________.
13.在电影票上,如果将“8排4号”记作(8,4),那么(10,15)表示___________.
14.如果将电影票上“6排3号”简记为(6,3),那么“10排12号”可表示为 .
15.如下图所示,A表示三经路与一纬路的十字路口,B表示一经路与三纬路的十字路口,如果用(3,1)→(3,2)→(3,3)→(2,3)→(1,3)表示A到B的一条路线,用同样的方式写出另外一条由A到B的一条路线:(3,1)→( )→( )→( ) → (1,3).
三、解答题
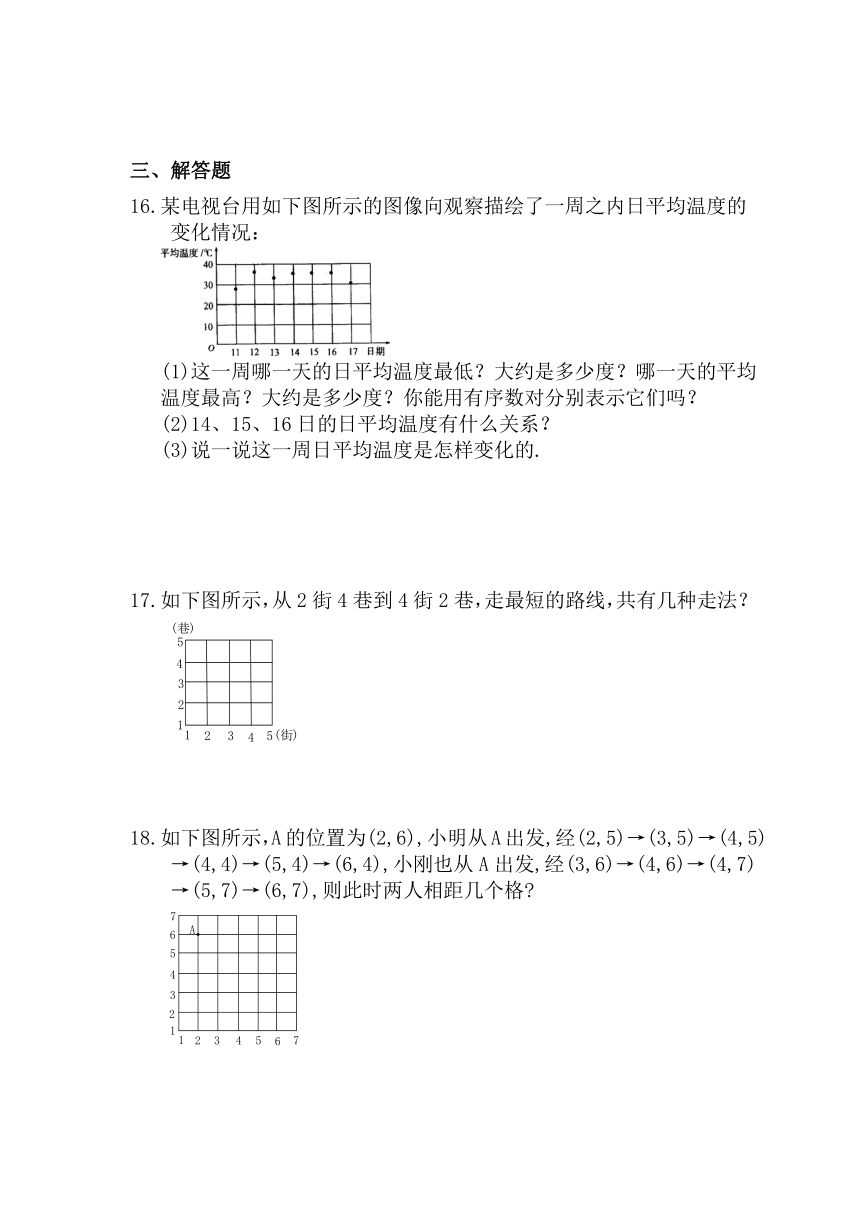
16.某电视台用如下图所示的图像向观察描绘了一周之内日平均温度的变化情况:
(1)这一周哪一天的日平均温度最低?大约是多少度?哪一天的平均温度最高?大约是多少度?你能用有序数对分别表示它们吗?
(2)14、15、16日的日平均温度有什么关系?
(3)说一说这一周日平均温度是怎样变化的.
17.如下图所示,从2街4巷到4街2巷,走最短的路线,共有几种走法?
18.如下图所示,A的位置为(2,6),小明从A出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格?
19.下图是一个动物园游览示意图,请你设计描述这个动物园图中每个景点位置的一个方法,并画图说明.
参考答案
答案为:B
答案为:A
答案为:D
答案为:C
答案为:C
答案为:A
答案为:C
答案为:B
答案为:C
答案为:B
答案为:3
答案为:九年级六班
答案为:10排15号
答案为:(10,12)
答案为:(2,1);(2,2);(2,3)
解:(1)11日的日平均温度最低,大约是28℃,用有序数对表示为(11,28),12日的日平均温度最高,大约是36℃,用有序数对表示为(12,36);
(2)14、15、16日的日平均温度相同,都是35℃;
(3)这周日平均温度从28℃升至36℃,然后降至33℃,又升至35℃,持续3天,周日降至30℃.
解:有6种走法分别为①(2,4)→(3,4)→(4,4)→(4,3)→(4,2);
②(2,4)→(3,4)→(3,3)→(4,3)→(4,2);
③(2,4)→(3,4)→(3,3)→(3,2)→(4,2);
④((2,4)→(2,3)→(3,3)→(4,3)→(4,2);
⑤(2,4)→(2,3)→(3,3)→(3,2)→(4,2);
⑥(2,4)→(2,3)→(2,2)→(3,2)→(4,2).
解:如下图所示,可知小明与小刚相距3个格.
解:如下图,标出行和列,可以确定马的位置为(3,3),那么南门的位置为(6,6),狮子的位置为(2,11),飞禽的位置为(9,10),两栖动物的位置为(10,7).
7.1.2 平面直角坐标系
知识点 1 平面直角坐标系的有关概念
1.如图,有5名同学分别画了一个平面直角坐标系,其中画法正确的是 (填序号).?
知识点 2 点的坐标
2.如图,点A的坐标是 ( )
A.(1,2) B.(21) C.2,1 D.(2,1)
3.在平面直角坐标系中,点P(-3,4)到x轴的距离为 ( )
A.3 B.-3 C.4 D.-4
4. 在如图所示的平面直角坐标系中描出下列各点:
A(4,3),B(1.5,-3.5),C(3,1),D(-2,3),E(2,0),F(-4,0),G(0,2),H(0,-3),M(-3,-2).
5. 如图,在平面直角坐标系中,描出下列各点,并写出各点的坐标.
(1)点A在x轴上,位于原点的左侧,距离坐标原点4个单位长度;
(2)点B在y轴上,位于原点的上侧,距离坐标原点4个单位长度;
(3)点C在y轴的左侧,在x轴的上侧,距离每个坐标轴都是4个单位长度.
知识点 3 各象限内、坐标轴上点的坐标特点
6. 在平面直角坐标系中,点A(a,2)在第二象限内,则a的取值可以是 ( )
A.1 B.- C. D.4或-4
7.在平面直角坐标系中,点(0,-10)在 ( )
A.x轴的正半轴上 B.x轴的负半轴上
C.y轴的正半轴上 D.y轴的负半轴上
8. 在平面直角坐标系中,第二象限内有一点M,点M到x轴的距离为5,到y轴的距离为4,则点M的坐标是 ( )
A.(5,4) B.(4,5)
C.(-4,5) D.(-5,4)
9. 在平面直角坐标系中,若点A(a,-b)在第三象限,则点B(-ab,b)所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
10.已知点P(3m-6,m+1),试分别根据下列条件,求出点P的坐标.
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大5.
11. 如图,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,6),点C在第一象限,则点C的坐标是 ( )
A.(6,3) B.(3,6)
C.(0,6) D.(6,6)
12.在平面直角坐标系中,点(-1,m2+1)一定在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
13.若点A(2,m)在x轴上,则点B(m-1,m+1)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
14.点P(m,5)和点Q(m,-1)的连线 ( )
A.与x轴平行
B.与y轴平行或重合
C.与x轴的夹角为50°
D.经过原点
15.到x轴的距离等于2的点组成的图形是 ( )
A.过点(0,2)且与x轴平行的直线
B.过点(2,0)且与y轴平行的直线
C.过点(0,-2)且与x轴平行的直线
D.分别过点(0,2)和点(0,-2)且与x轴平行的两条直线
16.已知线段AB=5,AB∥x轴,若点A的坐标为(-1,2),则点B的坐标为 .?
17.如图,如果用(0,0)表示点A,(1,0)表示点B,(1,2)表示点F.请按照这个规律建立平面直角坐标系,并表示出其他点的坐标.
18.已知点P(a-2,2a+8)到x轴、y轴的距离相等,求点P的坐标.
19.如图,已知点A(-2,3),B(4,3),C(-1,-3).
(1)求点C到x轴的距离;
(2)求三角形ABC的面积;
(3)点P在y轴上,当三角形ABP的面积为6时,请直接写出点P的坐标.
20.已知点A(-5,0),B(3,0).
(1)在y轴上有一点C满足S三角形ABC=16,求点C的坐标;
(2)在坐标平面上满足S三角形ABC=16的点C有多少个?这些点有什么规律?
参考答案
1.④ 2.D
3.C 解析: 点P(-3,4)到x轴的距离为|4|=4.
4.略
5.图略 (1)A(-4,0) (2)B(0,4) (3)C(-4,4)6.B 7.D
8.C 解析: 设点M的坐标是(x0,y0).
∵点M到x轴的距离为5,到y轴的距离为4,
∴|y0|=5,|x0|=4.
又∵点M在第二象限内,
∴x=-4,y=5,
∴点M的坐标为(-4,5).
故选C.
9.A 解析: ∵点A(a,-b)在第三象限,
∴a<0,-b<0,
∴b>0,
∴-ab>0,
故点B(-ab,b)所在的象限是第一象限.
故选A.
10.解:(1)因为点P(3m-6,m+1)在y轴上,
所以3m-6=0,解得m=2,
所以m+1=2+1=3,
所以点P的坐标为(0,3).
(2)因为点P(3m-6,m+1)在x轴上,
所以m+1=0,解得m=-1,
所以3m-6=3×(-1)-6=-9,
所以点P的坐标为(-9,0).
(3)因为点P(3m-6,m+1)的纵坐标比横坐标大5,所以m+1-(3m-6)=5,解得m=1,
所以3m-6=3×1-6=-3,m+1=1+1=2,
所以点P的坐标为(-3,2).
11.D 解析: 本题主要考查了点的坐标和正方形的性质,正确求出OB,BC的长度是解决本题的关键.利用O,D两点的坐标,求出OD的长度,利用正方形的性质求出OB,BC的长度,进而得出点C的坐标即可.∵O,D两点的坐标分别是(0,0),(0,6),∴OD=6.∵四边形OBCD是正方形,∴OB⊥BC,OB=BC=6,∴点C的坐标为(6,6).故选D.
12.B 解析: 因为m2+1>0,所以点(-1,m2+1)一定在第二象限.故选B.
13.B 解析: 因为点A(2,m)在x轴上,
所以m=0,所以m-1=-1<0,m+1=1>0,
所以点B在第二象限.
14.B 解析: 横坐标相同,纵坐标不同的两个点的连线与y轴平行或重合.
15.D 解析: 因为到x轴的距离等于2的点都在与x轴平行的两条直线上,即点的纵坐标为2和-2,所以到x轴的距离等于2的点组成的图形为分别过点(0,2)和(0,-2)且与x轴平行的两条直线.
16.(-6,2)或(4,2)
解析: 若点B在点A左边,因为线段AB=5,AB∥x轴,所以B(-6,2);若点B在点A右边,因为线段AB=5,AB∥x轴,所以B(4,2).
17.解:∵(0,0)表示点A,(1,0)表示点B,(1,2)表示点F,
∴建立平面直角坐标系如图所示,
∴C(2,0),D(2,1),E(2,2),G(0,2),H(0,1),P(1,1).
18.解:因为点P到x轴、y轴的距离相等,
所以a-2=2a+8或a-2+2a+8=0,
解得a=-10或a=-2.
当a=-10时,a-2=-12,2a+8=-12,
则P(-12,-12);
当a=-2时,a-2=-4,2a+8=4,
则P(-4,4).
综上所述,点P的坐标为(-12,-12)或(-4,4).
19.解:(1)∵C(-1,-3),|-3|=3,
∴点C到x轴的距离为3.
(2)∵A(-2,3),B(4,3),C(-1,-3),
∴AB=4-(-2)=6,点C到边AB的距离为3-(-3)=6,
∴三角形ABC的面积为6×6÷2=18.
(3)设点P的坐标为(0,y0).
∵三角形ABP的面积为6,A(-2,3),B(4,3),
∴×6×|y0-3|=6,
∴|y0-3|=2,∴y0=5或y0=1,
∴点P的坐标为(0,5)或(0,1).
20.解:(1)设点C的坐标为(0,t).因为AB=8,
所以S三角形ABC=AB·|yC|=×8|t|=16,
所以|t|=4,即t=±4,
所以点C的坐标为(0,4)或(0,-4).
(2)由(1)知|yC|=4的点C均满足条件,因此这样的点C有无数个,如图,它们分别在到x轴的距离等于4,且平行于x轴的两条直线l1与l2上.
一、选择题
1.下面的有序数对的写法正确的是( )
A.(1、3) B.(1,3) C.1,3 D.以上表达都正确
2.我们用以下表格来表示某超市的平面示意图.如果用(C,3)表示“体育用品”的位置,那么表示“儿童服装”的位置应记作( )
A.(A,3) B.(B,4) C.(C,2) D.(D,1)
3.体育课上,七年级某班49名同学在操场上练习正方形方队,他们站成7×7方队,每横队7人,每纵队7人,小敏在第2纵队的排头,记为(1,2),小娟在第5纵队的队尾,则小娟的位置应记为( )
A.(6,5) B.(5,6) C.(5,7) D.(7,5)
4.观察下表,若用有序实数对(m,n)表示第m行第n列的数,如:(4,3)表示实数6,则(20,18)表示的数是(???)
A.18???????? B.20?????? C.37 ??????D.38
5.下列关于有序数对的说法正确的是(?? )
A.(3,4)与(4,3)表示的位置相同
B.(a,b)与(b,a)表示的位置肯定不同
C.(3,5)与(5,3)是表示不同位置的两个有序数对
D.有序数对(2,2)与(2,2)表示两个不同的位置
6.七年级⑴班的座位共有6排8列,张军同学的座位在2排3列,我们可以记作(2,3),那么吴灏同学的座位在5排6列,应记作(?? )
A.(5,6)??? B.(6,5)?? ? C.(6,8)??? D.(3,2)
7.将正整数按如下图所示的规律排列,若用有序数对(m,n)表示从上到下第m行,和该行从左到右第n个数,如(4,2)表示整数8,则(8,4)表示的整数是( )
A.31 B.32 C.33 D.41
8.观察下列数对:(1,1) , (1,2) , (2,1) , (1,3) , (2,2) , (3,1) , (1,4) , (2,3) , (3,2) , (4,1) , (1,5) , (2,4)...那么第32个数对是( )
A.(4,4) B.(4,5) C.(4,6) D.(5,4)
9.如下图所示,图中是沈阳市地图简图的一部分,图中“故宫”、“鼓楼”所在的区域分别是( )
A.D7,E6 B.D6,E7 C.E7,D6 D.E6,D7
10.如下表所示,小聪家在A点,用(3,1)表示,小明家在B点,用(8,5)表示.若用(3,1)-(4,1)-(5,1)-(5,2)-(5,3)-(5,4)-(6,4)-(7,4)表示由A到B的一种走法,并规定从A到B只能向下或向右走.那么下面走法符合题意的有( )
A.(3,1)-(4,1)-(4,2)-(5,2)-(6,2)-(7,2)-(7,3)-(8,3)
B.(3,1)-(4,1)-(5,1)-(6,1)-(7,1)-(7,2)-(7,3)-(7,4)
C.(3,1)-(4,1)-(5,1)-(6,1)-(7,1)-(8,1)-(8,2)-(8,3)-(8,4)-(7,4)
D.(3,1)-(4,1)-(5,1)-(6,1)-(6,2)-(6,3)-(6,4)-(6,5)-(7,5)-(7,4)
二、填空题
11.下列说法中:①座位是4排2号;②某城市在东经118°,北纬29°;③某校在昌荣大道229号;④甲地距乙地2 km,其中能确定位置的有________个.
12.如果用(7,3)表示七年级三班,则(9,6)表示____________.
13.在电影票上,如果将“8排4号”记作(8,4),那么(10,15)表示___________.
14.如果将电影票上“6排3号”简记为(6,3),那么“10排12号”可表示为 .
15.如下图所示,A表示三经路与一纬路的十字路口,B表示一经路与三纬路的十字路口,如果用(3,1)→(3,2)→(3,3)→(2,3)→(1,3)表示A到B的一条路线,用同样的方式写出另外一条由A到B的一条路线:(3,1)→( )→( )→( ) → (1,3).
三、解答题
16.某电视台用如下图所示的图像向观察描绘了一周之内日平均温度的变化情况:
(1)这一周哪一天的日平均温度最低?大约是多少度?哪一天的平均温度最高?大约是多少度?你能用有序数对分别表示它们吗?
(2)14、15、16日的日平均温度有什么关系?
(3)说一说这一周日平均温度是怎样变化的.
17.如下图所示,从2街4巷到4街2巷,走最短的路线,共有几种走法?
18.如下图所示,A的位置为(2,6),小明从A出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格?
19.下图是一个动物园游览示意图,请你设计描述这个动物园图中每个景点位置的一个方法,并画图说明.
参考答案
答案为:B
答案为:A
答案为:D
答案为:C
答案为:C
答案为:A
答案为:C
答案为:B
答案为:C
答案为:B
答案为:3
答案为:九年级六班
答案为:10排15号
答案为:(10,12)
答案为:(2,1);(2,2);(2,3)
解:(1)11日的日平均温度最低,大约是28℃,用有序数对表示为(11,28),12日的日平均温度最高,大约是36℃,用有序数对表示为(12,36);
(2)14、15、16日的日平均温度相同,都是35℃;
(3)这周日平均温度从28℃升至36℃,然后降至33℃,又升至35℃,持续3天,周日降至30℃.
解:有6种走法分别为①(2,4)→(3,4)→(4,4)→(4,3)→(4,2);
②(2,4)→(3,4)→(3,3)→(4,3)→(4,2);
③(2,4)→(3,4)→(3,3)→(3,2)→(4,2);
④((2,4)→(2,3)→(3,3)→(4,3)→(4,2);
⑤(2,4)→(2,3)→(3,3)→(3,2)→(4,2);
⑥(2,4)→(2,3)→(2,2)→(3,2)→(4,2).
解:如下图所示,可知小明与小刚相距3个格.
解:如下图,标出行和列,可以确定马的位置为(3,3),那么南门的位置为(6,6),狮子的位置为(2,11),飞禽的位置为(9,10),两栖动物的位置为(10,7).
7.1.2 平面直角坐标系
知识点 1 平面直角坐标系的有关概念
1.如图,有5名同学分别画了一个平面直角坐标系,其中画法正确的是 (填序号).?
知识点 2 点的坐标
2.如图,点A的坐标是 ( )
A.(1,2) B.(21) C.2,1 D.(2,1)
3.在平面直角坐标系中,点P(-3,4)到x轴的距离为 ( )
A.3 B.-3 C.4 D.-4
4. 在如图所示的平面直角坐标系中描出下列各点:
A(4,3),B(1.5,-3.5),C(3,1),D(-2,3),E(2,0),F(-4,0),G(0,2),H(0,-3),M(-3,-2).
5. 如图,在平面直角坐标系中,描出下列各点,并写出各点的坐标.
(1)点A在x轴上,位于原点的左侧,距离坐标原点4个单位长度;
(2)点B在y轴上,位于原点的上侧,距离坐标原点4个单位长度;
(3)点C在y轴的左侧,在x轴的上侧,距离每个坐标轴都是4个单位长度.
知识点 3 各象限内、坐标轴上点的坐标特点
6. 在平面直角坐标系中,点A(a,2)在第二象限内,则a的取值可以是 ( )
A.1 B.- C. D.4或-4
7.在平面直角坐标系中,点(0,-10)在 ( )
A.x轴的正半轴上 B.x轴的负半轴上
C.y轴的正半轴上 D.y轴的负半轴上
8. 在平面直角坐标系中,第二象限内有一点M,点M到x轴的距离为5,到y轴的距离为4,则点M的坐标是 ( )
A.(5,4) B.(4,5)
C.(-4,5) D.(-5,4)
9. 在平面直角坐标系中,若点A(a,-b)在第三象限,则点B(-ab,b)所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
10.已知点P(3m-6,m+1),试分别根据下列条件,求出点P的坐标.
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大5.
11. 如图,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,6),点C在第一象限,则点C的坐标是 ( )
A.(6,3) B.(3,6)
C.(0,6) D.(6,6)
12.在平面直角坐标系中,点(-1,m2+1)一定在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
13.若点A(2,m)在x轴上,则点B(m-1,m+1)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
14.点P(m,5)和点Q(m,-1)的连线 ( )
A.与x轴平行
B.与y轴平行或重合
C.与x轴的夹角为50°
D.经过原点
15.到x轴的距离等于2的点组成的图形是 ( )
A.过点(0,2)且与x轴平行的直线
B.过点(2,0)且与y轴平行的直线
C.过点(0,-2)且与x轴平行的直线
D.分别过点(0,2)和点(0,-2)且与x轴平行的两条直线
16.已知线段AB=5,AB∥x轴,若点A的坐标为(-1,2),则点B的坐标为 .?
17.如图,如果用(0,0)表示点A,(1,0)表示点B,(1,2)表示点F.请按照这个规律建立平面直角坐标系,并表示出其他点的坐标.
18.已知点P(a-2,2a+8)到x轴、y轴的距离相等,求点P的坐标.
19.如图,已知点A(-2,3),B(4,3),C(-1,-3).
(1)求点C到x轴的距离;
(2)求三角形ABC的面积;
(3)点P在y轴上,当三角形ABP的面积为6时,请直接写出点P的坐标.
20.已知点A(-5,0),B(3,0).
(1)在y轴上有一点C满足S三角形ABC=16,求点C的坐标;
(2)在坐标平面上满足S三角形ABC=16的点C有多少个?这些点有什么规律?
参考答案
1.④ 2.D
3.C 解析: 点P(-3,4)到x轴的距离为|4|=4.
4.略
5.图略 (1)A(-4,0) (2)B(0,4) (3)C(-4,4)6.B 7.D
8.C 解析: 设点M的坐标是(x0,y0).
∵点M到x轴的距离为5,到y轴的距离为4,
∴|y0|=5,|x0|=4.
又∵点M在第二象限内,
∴x=-4,y=5,
∴点M的坐标为(-4,5).
故选C.
9.A 解析: ∵点A(a,-b)在第三象限,
∴a<0,-b<0,
∴b>0,
∴-ab>0,
故点B(-ab,b)所在的象限是第一象限.
故选A.
10.解:(1)因为点P(3m-6,m+1)在y轴上,
所以3m-6=0,解得m=2,
所以m+1=2+1=3,
所以点P的坐标为(0,3).
(2)因为点P(3m-6,m+1)在x轴上,
所以m+1=0,解得m=-1,
所以3m-6=3×(-1)-6=-9,
所以点P的坐标为(-9,0).
(3)因为点P(3m-6,m+1)的纵坐标比横坐标大5,所以m+1-(3m-6)=5,解得m=1,
所以3m-6=3×1-6=-3,m+1=1+1=2,
所以点P的坐标为(-3,2).
11.D 解析: 本题主要考查了点的坐标和正方形的性质,正确求出OB,BC的长度是解决本题的关键.利用O,D两点的坐标,求出OD的长度,利用正方形的性质求出OB,BC的长度,进而得出点C的坐标即可.∵O,D两点的坐标分别是(0,0),(0,6),∴OD=6.∵四边形OBCD是正方形,∴OB⊥BC,OB=BC=6,∴点C的坐标为(6,6).故选D.
12.B 解析: 因为m2+1>0,所以点(-1,m2+1)一定在第二象限.故选B.
13.B 解析: 因为点A(2,m)在x轴上,
所以m=0,所以m-1=-1<0,m+1=1>0,
所以点B在第二象限.
14.B 解析: 横坐标相同,纵坐标不同的两个点的连线与y轴平行或重合.
15.D 解析: 因为到x轴的距离等于2的点都在与x轴平行的两条直线上,即点的纵坐标为2和-2,所以到x轴的距离等于2的点组成的图形为分别过点(0,2)和(0,-2)且与x轴平行的两条直线.
16.(-6,2)或(4,2)
解析: 若点B在点A左边,因为线段AB=5,AB∥x轴,所以B(-6,2);若点B在点A右边,因为线段AB=5,AB∥x轴,所以B(4,2).
17.解:∵(0,0)表示点A,(1,0)表示点B,(1,2)表示点F,
∴建立平面直角坐标系如图所示,
∴C(2,0),D(2,1),E(2,2),G(0,2),H(0,1),P(1,1).
18.解:因为点P到x轴、y轴的距离相等,
所以a-2=2a+8或a-2+2a+8=0,
解得a=-10或a=-2.
当a=-10时,a-2=-12,2a+8=-12,
则P(-12,-12);
当a=-2时,a-2=-4,2a+8=4,
则P(-4,4).
综上所述,点P的坐标为(-12,-12)或(-4,4).
19.解:(1)∵C(-1,-3),|-3|=3,
∴点C到x轴的距离为3.
(2)∵A(-2,3),B(4,3),C(-1,-3),
∴AB=4-(-2)=6,点C到边AB的距离为3-(-3)=6,
∴三角形ABC的面积为6×6÷2=18.
(3)设点P的坐标为(0,y0).
∵三角形ABP的面积为6,A(-2,3),B(4,3),
∴×6×|y0-3|=6,
∴|y0-3|=2,∴y0=5或y0=1,
∴点P的坐标为(0,5)或(0,1).
20.解:(1)设点C的坐标为(0,t).因为AB=8,
所以S三角形ABC=AB·|yC|=×8|t|=16,
所以|t|=4,即t=±4,
所以点C的坐标为(0,4)或(0,-4).
(2)由(1)知|yC|=4的点C均满足条件,因此这样的点C有无数个,如图,它们分别在到x轴的距离等于4,且平行于x轴的两条直线l1与l2上.
