2020-2021学年度 人教版七年级数学下册 第五章 相交线与平行线 5.1.2 垂线 同步练习(word版含答案)
文档属性
| 名称 | 2020-2021学年度 人教版七年级数学下册 第五章 相交线与平行线 5.1.2 垂线 同步练习(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 146.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 00:00:00 | ||
图片预览


文档简介
第五章 相交线与平行线 5.1.2 垂线
1.下列选项中,过点P画AB的垂线CD,三角板放法正确的是( )
2.如图,经过直线l外一点A画l的垂线,能画出( )
A.1条 B.2条 C.3条 D.4条
3. 如图所示,点P到直线l的距离是( )
A.线段PA的长度 B.线段PB的长度
C.线段PC的长度 D.线段PD的长度
4.下列图形中线段PQ的长度表示P到直线a的距离的是( )
5.如图,已知ON⊥a,OM⊥a,所以OM与ON重合的理由是( )
A.过两点确定一条直线
B.在同一平面内,过一点有且只有一条直线垂直于已知直线
C.过两点能作一条垂线
D.两点之间线段最短
6. 下列条件中,两条直线的位置关系是互相垂直的有( )
①两条直线相交所成的四个角中有一个是直角;②两条直线相交,有一组邻补角相等;③两条直线相交,对顶角互补.
A.0个 B.1个 C.2个 D.3个
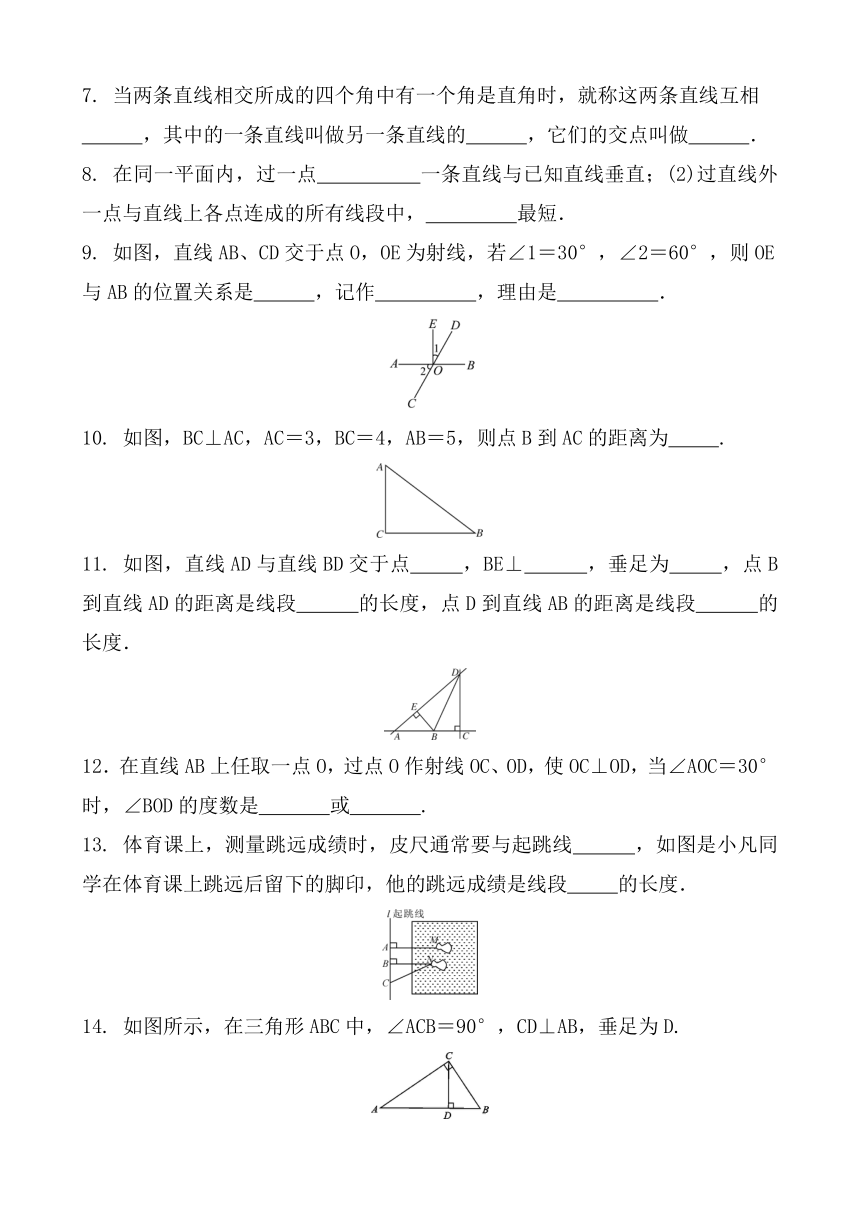
7. 当两条直线相交所成的四个角中有一个角是直角时,就称这两条直线互相
,其中的一条直线叫做另一条直线的 ,它们的交点叫做 .
8. 在同一平面内,过一点 一条直线与已知直线垂直;(2)过直线外一点与直线上各点连成的所有线段中, 最短.
9. 如图,直线AB、CD交于点O,OE为射线,若∠1=30°,∠2=60°,则OE与AB的位置关系是 ,记作 ,理由是 .
10. 如图,BC⊥AC,AC=3,BC=4,AB=5,则点B到AC的距离为 .
11. 如图,直线AD与直线BD交于点 ,BE⊥ ,垂足为 ,点B到直线AD的距离是线段 的长度,点D到直线AB的距离是线段 的长度.
12.在直线AB上任取一点O,过点O作射线OC、OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是 或 .
13. 体育课上,测量跳远成绩时,皮尺通常要与起跳线 ,如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段 的长度.
14. 如图所示,在三角形ABC中,∠ACB=90°,CD⊥AB,垂足为D.
若AC=4 cm,BC=3 cm,AB=5 cm,则点A到直线BC的距离为 cm,点B到直线AC的距离为 cm,点C到直线AB的距离为 cm.
15. 如图①,∠BAC为钝角.
(1)画出点C到AB的垂线;
(2)过点A画BC的垂线;
(3)过点B画AC的垂线.
16. 如图:
(1)过点A画BC的垂线,垂足为E;
(2)过点B画AD的垂线,垂足为F;
(3)过点C画AD的垂线,垂足为G;
(4)线段AE、AB、AD三者中最短的是哪一条,其依据是什么?
17. 如图,O为直线AB上一点,∠BOC=3∠AOC,OC平分∠AOD.
(1)求∠AOC的度数;
(2)推测OD与AB的位置关系,并说明理由.
18. 如图,两直线AB、CD相交于点O,已知OE平分∠BOD,且∠AOC∶∠AOD=3∶7.
(1)求∠DOE的度数;
(2)若OF⊥OE,求∠COF的度数.
19. 如图所示,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,求∠NOD的度数;
(2)若∠1=∠BOC,求∠BOD的度数.
20. 如图,一辆汽车在直线形的公路AB上由A向B行驶,M、N是分别位于AB两侧的村庄.
(1)设汽车行驶到公路AB上点P的位置时,距离村庄M最近,行驶到点Q的位置时,距离村庄N最近,请在图中的公路上分别画出P、Q的位置(保留画图痕迹);
(2)当汽车从A出发向B行驶时,在公路AB的哪一段路上距离M、N两村庄都越来越近?在哪一段路上距离村庄N越来越近,而距离村庄M却越来越远?
答案:
1---6 CABCD D
7. 垂直 垂线 垂足
8. 有且只有 垂线段
9. 垂直 OE⊥AB 垂直定义
10. 4
11. D AD E BE DC
12. 60° 120°
13. 垂直 NB
14. 4 3
15. 如图②所示:
(1)CF就是点C到AB的垂线
(2)AD就是点A到BC的垂线
(3)BE就是点B到AC的垂线
16. 解:(1)(2)(3)答案如图所示
(4)三条线段中最短的是线段AE,其依据是“垂线段最短”.
17. 解:(1)∠AOC=45°
(2)OD与AB垂直.理由:因为OC平分∠AOD,所以∠COD=∠AOC=45°,所以∠AOD=∠AOC+∠COD=45°+45°=90°,所以OD⊥AB
18. 解:(1)∵∠AOC∶∠AOD=3∶7,∠AOC+∠AOD=180°,
∴∠AOC=180°×=54°,∴∠BOD=54°,又∵OE平分∠BOD,
∴∠DOE=27°;
(2)∵OF⊥OE,∠DOE=27°,∴∠DOF=63°,∴∠COF=180°-63°=117°.
19. 解:(1)∵∠1+∠AOC=90°,而∠1=∠2,∴∠2+∠AOC=90°,
∴∠NOD=90°;
(2)设∠1的度数为x,则∠BOC的度数为4x,由∠BOC-∠1=90°得3x=90°,∴x=30°,∴∠BOD=180°-30°-90°=60°.
20. 解:(1)P、Q的位置如图所示:
(2)在AP段距离M、N两村庄都越来越近,在PQ段距离村庄N越来越近,而距离村庄M却越来越远.
1.下列选项中,过点P画AB的垂线CD,三角板放法正确的是( )
2.如图,经过直线l外一点A画l的垂线,能画出( )
A.1条 B.2条 C.3条 D.4条
3. 如图所示,点P到直线l的距离是( )
A.线段PA的长度 B.线段PB的长度
C.线段PC的长度 D.线段PD的长度
4.下列图形中线段PQ的长度表示P到直线a的距离的是( )
5.如图,已知ON⊥a,OM⊥a,所以OM与ON重合的理由是( )
A.过两点确定一条直线
B.在同一平面内,过一点有且只有一条直线垂直于已知直线
C.过两点能作一条垂线
D.两点之间线段最短
6. 下列条件中,两条直线的位置关系是互相垂直的有( )
①两条直线相交所成的四个角中有一个是直角;②两条直线相交,有一组邻补角相等;③两条直线相交,对顶角互补.
A.0个 B.1个 C.2个 D.3个
7. 当两条直线相交所成的四个角中有一个角是直角时,就称这两条直线互相
,其中的一条直线叫做另一条直线的 ,它们的交点叫做 .
8. 在同一平面内,过一点 一条直线与已知直线垂直;(2)过直线外一点与直线上各点连成的所有线段中, 最短.
9. 如图,直线AB、CD交于点O,OE为射线,若∠1=30°,∠2=60°,则OE与AB的位置关系是 ,记作 ,理由是 .
10. 如图,BC⊥AC,AC=3,BC=4,AB=5,则点B到AC的距离为 .
11. 如图,直线AD与直线BD交于点 ,BE⊥ ,垂足为 ,点B到直线AD的距离是线段 的长度,点D到直线AB的距离是线段 的长度.
12.在直线AB上任取一点O,过点O作射线OC、OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是 或 .
13. 体育课上,测量跳远成绩时,皮尺通常要与起跳线 ,如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段 的长度.
14. 如图所示,在三角形ABC中,∠ACB=90°,CD⊥AB,垂足为D.
若AC=4 cm,BC=3 cm,AB=5 cm,则点A到直线BC的距离为 cm,点B到直线AC的距离为 cm,点C到直线AB的距离为 cm.
15. 如图①,∠BAC为钝角.
(1)画出点C到AB的垂线;
(2)过点A画BC的垂线;
(3)过点B画AC的垂线.
16. 如图:
(1)过点A画BC的垂线,垂足为E;
(2)过点B画AD的垂线,垂足为F;
(3)过点C画AD的垂线,垂足为G;
(4)线段AE、AB、AD三者中最短的是哪一条,其依据是什么?
17. 如图,O为直线AB上一点,∠BOC=3∠AOC,OC平分∠AOD.
(1)求∠AOC的度数;
(2)推测OD与AB的位置关系,并说明理由.
18. 如图,两直线AB、CD相交于点O,已知OE平分∠BOD,且∠AOC∶∠AOD=3∶7.
(1)求∠DOE的度数;
(2)若OF⊥OE,求∠COF的度数.
19. 如图所示,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,求∠NOD的度数;
(2)若∠1=∠BOC,求∠BOD的度数.
20. 如图,一辆汽车在直线形的公路AB上由A向B行驶,M、N是分别位于AB两侧的村庄.
(1)设汽车行驶到公路AB上点P的位置时,距离村庄M最近,行驶到点Q的位置时,距离村庄N最近,请在图中的公路上分别画出P、Q的位置(保留画图痕迹);
(2)当汽车从A出发向B行驶时,在公路AB的哪一段路上距离M、N两村庄都越来越近?在哪一段路上距离村庄N越来越近,而距离村庄M却越来越远?
答案:
1---6 CABCD D
7. 垂直 垂线 垂足
8. 有且只有 垂线段
9. 垂直 OE⊥AB 垂直定义
10. 4
11. D AD E BE DC
12. 60° 120°
13. 垂直 NB
14. 4 3
15. 如图②所示:
(1)CF就是点C到AB的垂线
(2)AD就是点A到BC的垂线
(3)BE就是点B到AC的垂线
16. 解:(1)(2)(3)答案如图所示
(4)三条线段中最短的是线段AE,其依据是“垂线段最短”.
17. 解:(1)∠AOC=45°
(2)OD与AB垂直.理由:因为OC平分∠AOD,所以∠COD=∠AOC=45°,所以∠AOD=∠AOC+∠COD=45°+45°=90°,所以OD⊥AB
18. 解:(1)∵∠AOC∶∠AOD=3∶7,∠AOC+∠AOD=180°,
∴∠AOC=180°×=54°,∴∠BOD=54°,又∵OE平分∠BOD,
∴∠DOE=27°;
(2)∵OF⊥OE,∠DOE=27°,∴∠DOF=63°,∴∠COF=180°-63°=117°.
19. 解:(1)∵∠1+∠AOC=90°,而∠1=∠2,∴∠2+∠AOC=90°,
∴∠NOD=90°;
(2)设∠1的度数为x,则∠BOC的度数为4x,由∠BOC-∠1=90°得3x=90°,∴x=30°,∴∠BOD=180°-30°-90°=60°.
20. 解:(1)P、Q的位置如图所示:
(2)在AP段距离M、N两村庄都越来越近,在PQ段距离村庄N越来越近,而距离村庄M却越来越远.
