北师大版八年级数学下册课时达标训练:1.1.1三角形全等与等腰三角形的性质(word版含解析)
文档属性
| 名称 | 北师大版八年级数学下册课时达标训练:1.1.1三角形全等与等腰三角形的性质(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 147.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 22:42:26 | ||
图片预览


文档简介
1.1.1三角形全等与等腰三角形的性质
一、选择题
1.如图,点B,F,C,E在一条直线上,AB∥DE,AC∥DF,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.∠A=∠D
B.AC=DF
C.AB=DE
D.BF=EC
2.如图,在△ABC中,AD⊥BC于点D,D为BC的中点,则下列结论不正确的是
( )
A.△ABD≌△ACD
B.∠B=∠C
C.AD是∠BAC的平分线
D.△ABC是等边三角形
3.等腰三角形的一个外角等于100°,则与它不相邻的两个内角的度数分别为
( )
A.40°,40°
B.80°,20°
C.50°,50°
D.50°,50°或80°,20°
4.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在点O处相连并可绕点O转动,点C固定,OC=CD=DE,点D,E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是
( )
A.60°
B.65°
C.75°
D.80°
5.如图,在△ABC中,AC=BC,点D,E分别在AB,AC上,且AD=AE.连接DE,过点A的直线GH与DE平行,若∠C=40°,则∠GAD的度数为
( )
A.40°
B.45°
C.55°
D.70°
二、填空题
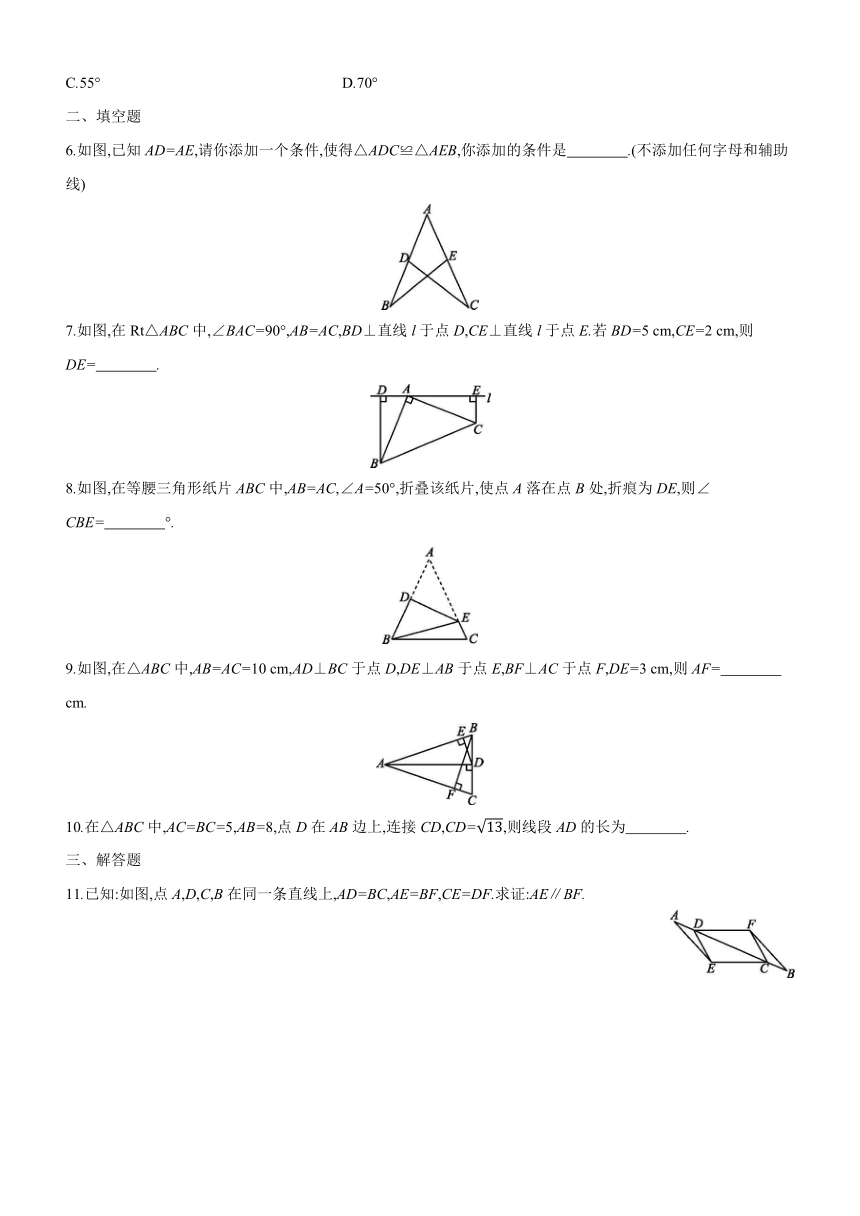
6.如图,已知AD=AE,请你添加一个条件,使得△ADC≌△AEB,你添加的条件是 .(不添加任何字母和辅助线)?
7.如图,在Rt△ABC中,∠BAC=90°,AB=AC,BD⊥直线l于点D,CE⊥直线l于点E.若BD=5
cm,CE=2
cm,则DE= .?
8.如图,在等腰三角形纸片ABC中,AB=AC,∠A=50°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE= °.?
9.如图,在△ABC中,AB=AC=10
cm,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=3
cm,则AF=
cm.?
10.在△ABC中,AC=BC=5,AB=8,点D在AB边上,连接CD,CD=,则线段AD的长为 .?
三、解答题
11.已知:如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF.求证:AE∥BF.
12.如图,在△ABC中,AB=AC,D是BC的中点,E,F分别是AB,AC边上的点,且AE=AF.求证:DE=DF.
13.
如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF,EF相交于点F.
求证:(1)∠C=∠BAD;
(2)AC=EF.
14.已知:如图,在△ABC中,AB=AC=20厘米,BC=16厘米,D为AB的中点.如果点P从点B出发沿B-C-A的路径以3厘米/秒的速度运动,点Q从点C出发沿C-A-B的路径运动.P,Q两点同时出发,同时停止,设运动时间为t秒.
(1)若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPD与△CQP是否全等?请说明理由;
(2)当t为何值时,直线PD将△ABC的周长分成两部分,且其中一部分的长度是另一部分长度的3倍?
(3)若点Q以1厘米/秒的速度从点C出发,点P以原来的运动速度从点B同时出发,则经过多长时间,点P追上点Q?
答案
1.解析:
A A.添加∠A=∠D不能判定△ABC≌△DEF,故本选项符合题意;B.添加AC=DF可用AAS进行判定,故本选项不符合题意;C.添加AB=DE可用AAS进行判定,故本选项不符合题意;D.添加BF=EC可得出BC=EF,然后可用ASA进行判定,故本选项不符合题意.故选A.
2.[答案]
D
3.解析:
D ∵一个外角等于100°,∴与这个外角相邻的内角是180°-100°=80°.①当80°角是顶角时,底角是×(180°-80°)=50°,所求两个内角的度数分别为50°,50°;②当80°角是底角时,顶角是180°-80°×2=20°,所求两个内角的度数分别为80°,20°.综上所述,与它不相邻的两个内角的度数分别为50°,50°或80°,20°.故选D.
4.解析:
D ∵OC=CD=DE,∴∠O=∠ODC,∠DCE=∠DEC,
∴∠DCE=∠DEC=∠O+∠ODC=2∠ODC.∵∠O+∠OED=3∠ODC=∠BDE=75°,
∴∠ODC=25°.∵∠CDE+∠ODC=180°-∠BDE=105°,∴∠CDE=105°-∠ODC=80°.故选D.
5.解析:
C ∵AC=BC,∠C=40°,∴∠BAC=∠B=×(180°-40°)=70°.
∵AD=AE,∴∠ADE=∠AED=×(180°-70°)=55°.
∵GH∥DE,∴∠GAD=∠ADE=55°.故选C.
6.[答案]
AB=AC或∠ADC=∠AEB或∠B=∠C等(答案不唯一)
解析:
∵∠A=∠A,AD=AE,∴可以添加AB=AC,此时满足SAS;添加条件∠ADC=∠AEB,此时满足ASA;添加条件∠B=∠C,此时满足AAS.
7.[答案]
7
cm
解析:
∵∠BAC=90°,∠ADB=∠CEA=90°,∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,
∴∠CAE=∠ABD.在△ABD和△CAE中,∵∠ADB=∠CEA,∠ABD=∠CAE,AB=CA,
∴△ABD≌△CAE(AAS),∴AD=CE,BD=AE,∴DE=AD+AE=CE+BD=7
cm.故答案为7
cm.
8.[答案]
15
解析:
∵AB=AC,∠A=50°,∴∠ACB=∠ABC=×(180°-50°)=65°.∵将△ABC折叠,使点A落在点B处,折痕为DE,∠A=50°,∴∠ABE=∠A=50°,∴∠CBE=∠ABC-∠ABE=65°-50°=15°.故答案为15.
9.[答案]
8
解析:
∵在△ABC中,AB=AC=10
cm,AD⊥BC,∴AD是△ABC的中线,∴S△ABC=2S△ABD=2×AB·DE=AB·DE=30(cm2).∵S△ABC=AC·BF,∴×10·BF=30,
∴BF=6
cm.在Rt△ABF中,由勾股定理,得AF===8(cm).故答案为8.
10.[答案]
2或6
解析:
过点C作底边AB上的高CE.
∵AC=BC=5,AB=8,∴AE=4,
∴CE===3,
∴DE===2.
如图①,AD=AE-DE=2;如图②,AD=AE+DE=6.故线段AD的长为2或6.
11.证明:∵AD=BC,∴AC=BD.
在△ACE和△BDF中,
∵AC=BD,AE=BF,CE=DF,
∴△ACE≌△BDF(SSS),
∴∠A=∠B,∴AE∥BF.
12.证明:∵AB=AC,AE=AF,
∴∠B=∠C,BE=CF.
∵D是BC的中点,∴BD=CD.
在△BED和△CFD中,
∵BE=CF,∠B=∠C,BD=CD,
∴△BED≌△CFD(SAS),∴DE=DF.
13.证明:(1)∵AB=AE,D为线段BE的中点,
∴AD⊥BC,∴∠C+∠DAC=90°.
∵∠BAC=90°,∴∠BAD+∠DAC=90°,
∴∠C=∠BAD.
(2)∵AF∥BC,∴∠FAE=∠AEB.
∵AB=AE,∴∠B=∠AEB,
∴∠B=∠FAE.
又∵∠BAC=∠AEF=90°,AB=EA,
∴△ABC≌△EAF(ASA),∴AC=EF.
14.解:(1)全等.
理由如下:∵t=2,
∴BP=CQ=3×2=6(厘米).
∵AB=20厘米,D为AB的中点,
∴DB=10厘米.
∵PC=BC-BP=16-6=10(厘米),
∴PC=DB.
∵AB=AC,∴∠B=∠C,
∴△BPD≌△CQP(SAS).
(2)若点P在BC上移动,则16-3t+20+10=
3(10+3t),解得t=,符合题意;
若点P在AC上移动,则有3t+10=3[20-(3t-16)+10],解得t=,符合题意.
故当t=或时,直线PD将△ABC的周长分成两部分,且其中一部分的长度是另一部分长度的3倍.
(3)根据题意,得3t=t+16,解得t=8.
经检验,t=8符合题意.
∴经过8秒,点P追上点Q.
一、选择题
1.如图,点B,F,C,E在一条直线上,AB∥DE,AC∥DF,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.∠A=∠D
B.AC=DF
C.AB=DE
D.BF=EC
2.如图,在△ABC中,AD⊥BC于点D,D为BC的中点,则下列结论不正确的是
( )
A.△ABD≌△ACD
B.∠B=∠C
C.AD是∠BAC的平分线
D.△ABC是等边三角形
3.等腰三角形的一个外角等于100°,则与它不相邻的两个内角的度数分别为
( )
A.40°,40°
B.80°,20°
C.50°,50°
D.50°,50°或80°,20°
4.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在点O处相连并可绕点O转动,点C固定,OC=CD=DE,点D,E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是
( )
A.60°
B.65°
C.75°
D.80°
5.如图,在△ABC中,AC=BC,点D,E分别在AB,AC上,且AD=AE.连接DE,过点A的直线GH与DE平行,若∠C=40°,则∠GAD的度数为
( )
A.40°
B.45°
C.55°
D.70°
二、填空题
6.如图,已知AD=AE,请你添加一个条件,使得△ADC≌△AEB,你添加的条件是 .(不添加任何字母和辅助线)?
7.如图,在Rt△ABC中,∠BAC=90°,AB=AC,BD⊥直线l于点D,CE⊥直线l于点E.若BD=5
cm,CE=2
cm,则DE= .?
8.如图,在等腰三角形纸片ABC中,AB=AC,∠A=50°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE= °.?
9.如图,在△ABC中,AB=AC=10
cm,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=3
cm,则AF=
cm.?
10.在△ABC中,AC=BC=5,AB=8,点D在AB边上,连接CD,CD=,则线段AD的长为 .?
三、解答题
11.已知:如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF.求证:AE∥BF.
12.如图,在△ABC中,AB=AC,D是BC的中点,E,F分别是AB,AC边上的点,且AE=AF.求证:DE=DF.
13.
如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF,EF相交于点F.
求证:(1)∠C=∠BAD;
(2)AC=EF.
14.已知:如图,在△ABC中,AB=AC=20厘米,BC=16厘米,D为AB的中点.如果点P从点B出发沿B-C-A的路径以3厘米/秒的速度运动,点Q从点C出发沿C-A-B的路径运动.P,Q两点同时出发,同时停止,设运动时间为t秒.
(1)若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPD与△CQP是否全等?请说明理由;
(2)当t为何值时,直线PD将△ABC的周长分成两部分,且其中一部分的长度是另一部分长度的3倍?
(3)若点Q以1厘米/秒的速度从点C出发,点P以原来的运动速度从点B同时出发,则经过多长时间,点P追上点Q?
答案
1.解析:
A A.添加∠A=∠D不能判定△ABC≌△DEF,故本选项符合题意;B.添加AC=DF可用AAS进行判定,故本选项不符合题意;C.添加AB=DE可用AAS进行判定,故本选项不符合题意;D.添加BF=EC可得出BC=EF,然后可用ASA进行判定,故本选项不符合题意.故选A.
2.[答案]
D
3.解析:
D ∵一个外角等于100°,∴与这个外角相邻的内角是180°-100°=80°.①当80°角是顶角时,底角是×(180°-80°)=50°,所求两个内角的度数分别为50°,50°;②当80°角是底角时,顶角是180°-80°×2=20°,所求两个内角的度数分别为80°,20°.综上所述,与它不相邻的两个内角的度数分别为50°,50°或80°,20°.故选D.
4.解析:
D ∵OC=CD=DE,∴∠O=∠ODC,∠DCE=∠DEC,
∴∠DCE=∠DEC=∠O+∠ODC=2∠ODC.∵∠O+∠OED=3∠ODC=∠BDE=75°,
∴∠ODC=25°.∵∠CDE+∠ODC=180°-∠BDE=105°,∴∠CDE=105°-∠ODC=80°.故选D.
5.解析:
C ∵AC=BC,∠C=40°,∴∠BAC=∠B=×(180°-40°)=70°.
∵AD=AE,∴∠ADE=∠AED=×(180°-70°)=55°.
∵GH∥DE,∴∠GAD=∠ADE=55°.故选C.
6.[答案]
AB=AC或∠ADC=∠AEB或∠B=∠C等(答案不唯一)
解析:
∵∠A=∠A,AD=AE,∴可以添加AB=AC,此时满足SAS;添加条件∠ADC=∠AEB,此时满足ASA;添加条件∠B=∠C,此时满足AAS.
7.[答案]
7
cm
解析:
∵∠BAC=90°,∠ADB=∠CEA=90°,∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,
∴∠CAE=∠ABD.在△ABD和△CAE中,∵∠ADB=∠CEA,∠ABD=∠CAE,AB=CA,
∴△ABD≌△CAE(AAS),∴AD=CE,BD=AE,∴DE=AD+AE=CE+BD=7
cm.故答案为7
cm.
8.[答案]
15
解析:
∵AB=AC,∠A=50°,∴∠ACB=∠ABC=×(180°-50°)=65°.∵将△ABC折叠,使点A落在点B处,折痕为DE,∠A=50°,∴∠ABE=∠A=50°,∴∠CBE=∠ABC-∠ABE=65°-50°=15°.故答案为15.
9.[答案]
8
解析:
∵在△ABC中,AB=AC=10
cm,AD⊥BC,∴AD是△ABC的中线,∴S△ABC=2S△ABD=2×AB·DE=AB·DE=30(cm2).∵S△ABC=AC·BF,∴×10·BF=30,
∴BF=6
cm.在Rt△ABF中,由勾股定理,得AF===8(cm).故答案为8.
10.[答案]
2或6
解析:
过点C作底边AB上的高CE.
∵AC=BC=5,AB=8,∴AE=4,
∴CE===3,
∴DE===2.
如图①,AD=AE-DE=2;如图②,AD=AE+DE=6.故线段AD的长为2或6.
11.证明:∵AD=BC,∴AC=BD.
在△ACE和△BDF中,
∵AC=BD,AE=BF,CE=DF,
∴△ACE≌△BDF(SSS),
∴∠A=∠B,∴AE∥BF.
12.证明:∵AB=AC,AE=AF,
∴∠B=∠C,BE=CF.
∵D是BC的中点,∴BD=CD.
在△BED和△CFD中,
∵BE=CF,∠B=∠C,BD=CD,
∴△BED≌△CFD(SAS),∴DE=DF.
13.证明:(1)∵AB=AE,D为线段BE的中点,
∴AD⊥BC,∴∠C+∠DAC=90°.
∵∠BAC=90°,∴∠BAD+∠DAC=90°,
∴∠C=∠BAD.
(2)∵AF∥BC,∴∠FAE=∠AEB.
∵AB=AE,∴∠B=∠AEB,
∴∠B=∠FAE.
又∵∠BAC=∠AEF=90°,AB=EA,
∴△ABC≌△EAF(ASA),∴AC=EF.
14.解:(1)全等.
理由如下:∵t=2,
∴BP=CQ=3×2=6(厘米).
∵AB=20厘米,D为AB的中点,
∴DB=10厘米.
∵PC=BC-BP=16-6=10(厘米),
∴PC=DB.
∵AB=AC,∴∠B=∠C,
∴△BPD≌△CQP(SAS).
(2)若点P在BC上移动,则16-3t+20+10=
3(10+3t),解得t=,符合题意;
若点P在AC上移动,则有3t+10=3[20-(3t-16)+10],解得t=,符合题意.
故当t=或时,直线PD将△ABC的周长分成两部分,且其中一部分的长度是另一部分长度的3倍.
(3)根据题意,得3t=t+16,解得t=8.
经检验,t=8符合题意.
∴经过8秒,点P追上点Q.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
