2020-2021学年高二数学人教A版(2019)选择性必修三6.2.1排列 课件(共31张PPT)
文档属性
| 名称 | 2020-2021学年高二数学人教A版(2019)选择性必修三6.2.1排列 课件(共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 896.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
6.2 排列与组合
6.2.1 排列
分类加法计数原理(加法原理)
完成一件事有两类不同方案,在第1类方案中有m种
不同的方法,在第2类方案中有n种不同的方法,那么
完成这件事共有: 种不同的方法.
分步乘法计数原理(乘法原理)
完成一件事需要分成两个步骤,做第1步有m种不同
的方法,做第2步有n种不同的方法,那么完成这件
事共有: 种不同的方法.
分类加法计数原理与“分类”有关,各种方法相互独立,用其中任何一种方法都可以完成这件事;
分步乘法计数原理与“分步”有关,各个步骤相互依存,只有各个步骤都完成了,这件事才算完成.
五个人排成一队有多少种排法?
等公交车时的站队问题
通过解决实际的计数问题,得到排列的定义,并能够利用定义判断排列问题.
(重点)排列的定义
(难点)将实际问题中的具体对象抽象为元素,得到排列的定义.
学习目标:
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
【解题关键】把题目转化为从甲、乙、丙3名同学中选2名,按照参加上午的活动在前,参加下午的活动在后的顺序排列,求一共有多少种不同的排法?
探究点1 排列
上午
下午
相应的排法
甲
乙
丙
乙
甲
丙
丙
甲
乙
甲丙
甲乙
乙甲
乙丙
丙甲
丙乙
第一步:确定参加上午活动的同学即从3名中任 选1名,有3种选法.
第二步:确定参加下午活动的同学,有2种方法
根据分步计数原理:3×2=6 即共6种方法.
如果把上面问题中被取的对象叫做元素,那么问题可以叙述为:
从3个不同的元素a,b,c中任取2个,然后按照一定的顺序排成一列,一共有多少种不同的排列方法?
所有不同的排列是
ab, ac, ba, bc, ca, cb
不同的排列方法种数为
3×2=6.
问题2.从1,2,3,4这 4 个数字中,每次取出3个
排成一个三位数,共可得到多少个不同的三位数?
【解题关键】解决这个问题分三个步骤:
第一步先确定百位上的数,在4个数字中任取1个,有4种方法;
第二步确定中间的数,从余下的3个数中去取,有3种方法;
第三步确定右边的数,从余下的2个数中去取,有2种方法.
由分步乘法计数原理共有:4×3×2=24种不同的方法,用树形图排出,并写出所有的排列,由此可写出所有的排法.
解:从 4 个数字中,每次取出 3 个,按“百”
“十”“个”位的顺序排成一列,就得到一个三位数.因此有多少种不同的排列方法就有多少个不同的三位数.可以分三个步骤来解决这个问题:
第 1 步,确定百位上的数字,在 1 , 2 , 3 , 4
这 4 个数字中任取 1 个,有 4 种方法;
第 2 步,确定十位上的数字,当百位上的数字确定
后,十位上的数字只能从余下的 3 个数字中
去取,有 3 种方法;
第 3 步,确定个位上的数字,当百位、十位上的数
字确定后,个位的数字只能从余下的 2 个数
字中去取,有 2 种方法.
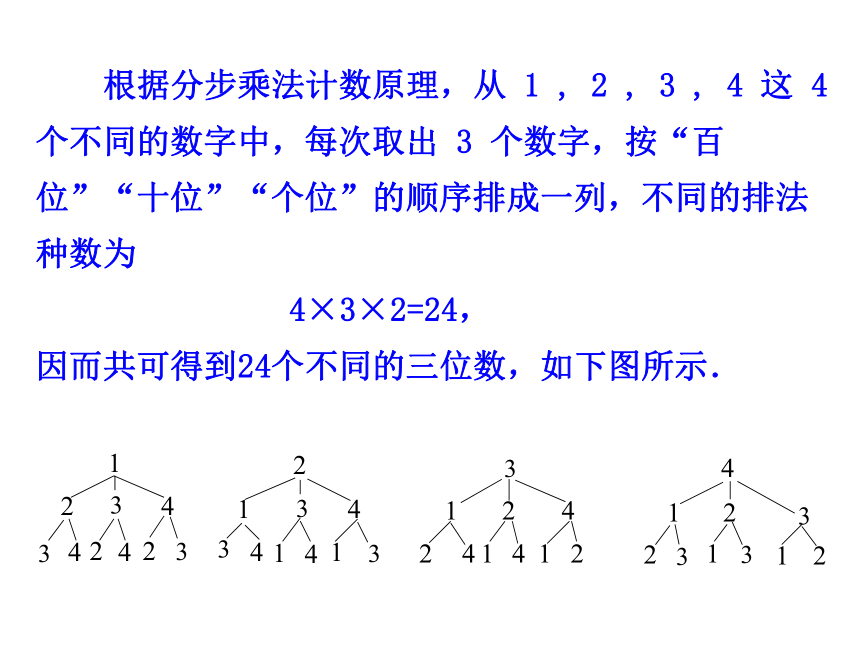
根据分步乘法计数原理,从 1 , 2 , 3 , 4 这 4 个不同的数字中,每次取出 3 个数字,按“百位”“十位”“个位”的顺序排成一列,不同的排法种数为
4×3×2=24,
因而共可得到24个不同的三位数,如下图所示.
由此可写出所有的三位数:
123,124,132,134,142,143,
213,214,231,234,241,243,
312,314,321,324,341,342,
412,413,421,423,431,432.
同样,问题2可以归结为:
从4个不同的元素a,b,c,d中任意取出3个,并按照一定的顺序排成一列,共有多少种不同的排列方法?
所有不同的排列是
abc,abd,acb, acd,adb,adc,
bac, bad,bca,bcd,bda,bdc
cab,cad,cba,cbd,cda,cdb
dab,dac,dba,dbc,dca,dcb.
不同的排列方法种数为
4×3×2=24.
问题3.问题1、问题2的共同特点是什么?你能将它们推广到一般情形吗?
定义:一般地,从n个不同元素中取出m (m ≤ n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
排列的特征:
1.排列的两个基本内容:
一是取出元素,二是按照一定顺序排列.
2.两个排列相同的条件:
元素相同,元素的顺序也一定相同.
说明:
1.元素不能重复.n个元素不能重复,m个元素也不能重复.
2.“按一定顺序”就是与位置有关,这是判断一个问题是否是排列问题的关键.
3.根据排列定义,两个排列相同的充要条件是:
两个排列的元素完全相同,且元素的排列顺序也相同.
如:123和125不相同,123和321也不相同
4.为了使写出的所有排列情况既不重复也不遗漏,最好采用“树形图”.
排列中的列举问题-树状图
1.适用范围:解决排列元素个数不多的问题.
2.策略:在操作中先将元素按照一定顺序排出,然后以先安排哪个元素为分类标准进行分类,再安排第二个元素,并按此元素分类,依次进行,直到完成一个排列,这样能做到不重不漏,然后按照树状图写出排列.
【例】从0,1,2,3这四个数字中,每次取出三个不同的数字排成一个三位数.能组成多少个不同的三位数,并写出这些三位数.
解析:组成三位数分三个步骤:
第一步:选百位上的数字,0不能排在首位,故有3种不同的排法;
第二步:选十位上的数字,有3种不同的排法;
第三步:选个位上的数字,有2种不同的排法.
由分步乘法计数原理得共有3×3×2=18(个)不同的三位数.
画出树状图:
由树状图知,所有的三位数为102,103,120,123,130,132,201,203,210,213,230,231,301,302,310,312,320,321.
下列问题是排列问题吗?请说明理由.
(1)从1,2,3,4四个数字中,任选两个做减法,其结果有多少种不同的可能?
(2)从1,2,3,4四个数字中,任选两个做乘法,其结果有多少种不同的可能?
(3)有12个车站,共需准备多少种车票?
(4)从学号1到10的十名同学中任抽两名同学去学校开座谈会,有多少种选法?
(5)平面上有5个点,其中任意三点不共线,这5点最多可确定多少条直线?
【即时训练】
问题 各问题研析 结果
(1) 由减法定义知,结果都与两数相减的顺序有关,故(1)是排列 (1)
(3)
(2) 由乘法定义知,结果都与两数相乘的顺序无关,故(2)不是排列 (3) 车票与始点站和终点站有关,由排列定义知(3)是排列 (4) 所选取两名同学参加座谈会,无顺序之分,故(4)不是排列 (5) 两点确定一条直线,与两点顺序无关,故(5)不是排列 解:
是否有顺序,有顺序且是从n个不同的元素中任取m(m≤n)个不同的元素的问题就是排列,否则就不是排列,
【总结提升】
判断一个问题是否为排列问题的依据
检验它是否有顺序的依据
变换元素的位置,看其结果是否有变化,有变化就是有顺序,无变化就是无顺序.
判断下列问题是否是排列问题:
(1)某班共有50名同学,现要投票选举正、副班长各一人,共有多少种可能的选举结果?
(2)从2,3,5,7,9中任取两数分别作对数的底数和指数,有多少不同对数值?
(3)从1到10十个自然数中任取两个数组成点的坐标,可得多少个不同的点的坐标?
【变式练习】
(4)从集合M={1,2,…,9}中,任取相异的两个
元素作为a,b,可以得到多少个焦点在x轴上的椭
圆方程
解: (1)是排列问题.选出的2人,担任正、副班长任意,与顺序有关,所以该问题是排列问题.
(2)是排列问题.显然对数值与底数和真数的取值的不同有关系,与顺序有关.
(3)是排列问题.任取两个数组成点的坐标,横、纵坐标的顺序不同,即为不同的坐标,与顺序有关.
(4)不是排列问题.焦点在x轴上的椭圆,方程中的a、b必有a>b,a、b的大小一定.
应用举例:
【例1】某省中学生足球赛预选赛每组有6支队,每支队都要与同组的其他队在主、客场分别比赛一场,那么每组共进行多少场比赛?
分析:每组任意2支队之间进行的一场比赛,可以看做是从该组6支队中选取2支,按“主队、客队”的顺序排成的一个排列.
解:从6支队伍中选2支,按“主队、客队”进行排列,分两步,第一步选1支做主队,有6种选法,第二步从剩下的5支队中选1支做客队,按照乘法计数原理,每组进行的比赛场次为 6×5=30.
【例2】(1)一张餐桌上有5盘不同的菜,甲、乙、丙3名同学每人从中各取1盘菜,共有多少种不同的取法?
(2)学校食堂的一个窗口共卖5种菜,甲、乙、丙3名同学每人从中选1种,共有多少种不同的选法?
分析:3名同学每人从5盘不同的菜中取1盘菜,可以看做是从这5盘菜中选取3盘,放在3个位置(给3名同学)的一个排列;而3名同学每人从食堂窗口的5种菜中选1种,每人都有5种选法,不能看成一个排列。
解:(1)可以先从这盘菜中取1盘给同学甲,然后从剩下的4盘菜中取1盘给同学乙,然最后从剩下的3盘菜中取1盘给同学丙,按乘法分步计数原理,不同的选法种数为 5×4×3=60.
(2)可以先让甲同学从5种菜中选1种,有5种选法;再让乙同学从5种菜中选1种,也有5种选法;最后让丙同学从5种菜中选1种,同样有5种选法.按乘法分步计数原理,不同的选法种数为 5×5×5=125.
【练习】
课本:P16 练习题
1.下列问题中:
(1)10本不同的书分给10名同学,每人一本;
(2)10位同学互通一次电话;
(3)10位同学互通一封信;
(4)10个没有任何三点共线的点构成的线段.
属于排列的有( )
A.1个 B.2个 C.3个 D.4个
解:(1)(3)是排列问题,(2)(4)不是排列问题.
B
2.用1,2,3,4四个数字排成三位数,并把这些三位数从小到大排成一个数列{an}.
(1)写出这个数列的前11项.
(2)这个数列共有多少项.
解:(1)111,112,113,114,121,122,123,124,
131,132,133.
(2)这个数列的项数就是用1,2,3,4排成三位数的个数,每一位都有4种排法,则共有4×4×4=64(项).
排列
按一定顺序排列
取出元素
不仅与选取的元素有关
而且与选取的元素排列顺序有关
布置作业:
1.完成课本P26 习题6.2第5,9题;
2.课时训练三。
6.2 排列与组合
6.2.1 排列
分类加法计数原理(加法原理)
完成一件事有两类不同方案,在第1类方案中有m种
不同的方法,在第2类方案中有n种不同的方法,那么
完成这件事共有: 种不同的方法.
分步乘法计数原理(乘法原理)
完成一件事需要分成两个步骤,做第1步有m种不同
的方法,做第2步有n种不同的方法,那么完成这件
事共有: 种不同的方法.
分类加法计数原理与“分类”有关,各种方法相互独立,用其中任何一种方法都可以完成这件事;
分步乘法计数原理与“分步”有关,各个步骤相互依存,只有各个步骤都完成了,这件事才算完成.
五个人排成一队有多少种排法?
等公交车时的站队问题
通过解决实际的计数问题,得到排列的定义,并能够利用定义判断排列问题.
(重点)排列的定义
(难点)将实际问题中的具体对象抽象为元素,得到排列的定义.
学习目标:
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
【解题关键】把题目转化为从甲、乙、丙3名同学中选2名,按照参加上午的活动在前,参加下午的活动在后的顺序排列,求一共有多少种不同的排法?
探究点1 排列
上午
下午
相应的排法
甲
乙
丙
乙
甲
丙
丙
甲
乙
甲丙
甲乙
乙甲
乙丙
丙甲
丙乙
第一步:确定参加上午活动的同学即从3名中任 选1名,有3种选法.
第二步:确定参加下午活动的同学,有2种方法
根据分步计数原理:3×2=6 即共6种方法.
如果把上面问题中被取的对象叫做元素,那么问题可以叙述为:
从3个不同的元素a,b,c中任取2个,然后按照一定的顺序排成一列,一共有多少种不同的排列方法?
所有不同的排列是
ab, ac, ba, bc, ca, cb
不同的排列方法种数为
3×2=6.
问题2.从1,2,3,4这 4 个数字中,每次取出3个
排成一个三位数,共可得到多少个不同的三位数?
【解题关键】解决这个问题分三个步骤:
第一步先确定百位上的数,在4个数字中任取1个,有4种方法;
第二步确定中间的数,从余下的3个数中去取,有3种方法;
第三步确定右边的数,从余下的2个数中去取,有2种方法.
由分步乘法计数原理共有:4×3×2=24种不同的方法,用树形图排出,并写出所有的排列,由此可写出所有的排法.
解:从 4 个数字中,每次取出 3 个,按“百”
“十”“个”位的顺序排成一列,就得到一个三位数.因此有多少种不同的排列方法就有多少个不同的三位数.可以分三个步骤来解决这个问题:
第 1 步,确定百位上的数字,在 1 , 2 , 3 , 4
这 4 个数字中任取 1 个,有 4 种方法;
第 2 步,确定十位上的数字,当百位上的数字确定
后,十位上的数字只能从余下的 3 个数字中
去取,有 3 种方法;
第 3 步,确定个位上的数字,当百位、十位上的数
字确定后,个位的数字只能从余下的 2 个数
字中去取,有 2 种方法.
根据分步乘法计数原理,从 1 , 2 , 3 , 4 这 4 个不同的数字中,每次取出 3 个数字,按“百位”“十位”“个位”的顺序排成一列,不同的排法种数为
4×3×2=24,
因而共可得到24个不同的三位数,如下图所示.
由此可写出所有的三位数:
123,124,132,134,142,143,
213,214,231,234,241,243,
312,314,321,324,341,342,
412,413,421,423,431,432.
同样,问题2可以归结为:
从4个不同的元素a,b,c,d中任意取出3个,并按照一定的顺序排成一列,共有多少种不同的排列方法?
所有不同的排列是
abc,abd,acb, acd,adb,adc,
bac, bad,bca,bcd,bda,bdc
cab,cad,cba,cbd,cda,cdb
dab,dac,dba,dbc,dca,dcb.
不同的排列方法种数为
4×3×2=24.
问题3.问题1、问题2的共同特点是什么?你能将它们推广到一般情形吗?
定义:一般地,从n个不同元素中取出m (m ≤ n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
排列的特征:
1.排列的两个基本内容:
一是取出元素,二是按照一定顺序排列.
2.两个排列相同的条件:
元素相同,元素的顺序也一定相同.
说明:
1.元素不能重复.n个元素不能重复,m个元素也不能重复.
2.“按一定顺序”就是与位置有关,这是判断一个问题是否是排列问题的关键.
3.根据排列定义,两个排列相同的充要条件是:
两个排列的元素完全相同,且元素的排列顺序也相同.
如:123和125不相同,123和321也不相同
4.为了使写出的所有排列情况既不重复也不遗漏,最好采用“树形图”.
排列中的列举问题-树状图
1.适用范围:解决排列元素个数不多的问题.
2.策略:在操作中先将元素按照一定顺序排出,然后以先安排哪个元素为分类标准进行分类,再安排第二个元素,并按此元素分类,依次进行,直到完成一个排列,这样能做到不重不漏,然后按照树状图写出排列.
【例】从0,1,2,3这四个数字中,每次取出三个不同的数字排成一个三位数.能组成多少个不同的三位数,并写出这些三位数.
解析:组成三位数分三个步骤:
第一步:选百位上的数字,0不能排在首位,故有3种不同的排法;
第二步:选十位上的数字,有3种不同的排法;
第三步:选个位上的数字,有2种不同的排法.
由分步乘法计数原理得共有3×3×2=18(个)不同的三位数.
画出树状图:
由树状图知,所有的三位数为102,103,120,123,130,132,201,203,210,213,230,231,301,302,310,312,320,321.
下列问题是排列问题吗?请说明理由.
(1)从1,2,3,4四个数字中,任选两个做减法,其结果有多少种不同的可能?
(2)从1,2,3,4四个数字中,任选两个做乘法,其结果有多少种不同的可能?
(3)有12个车站,共需准备多少种车票?
(4)从学号1到10的十名同学中任抽两名同学去学校开座谈会,有多少种选法?
(5)平面上有5个点,其中任意三点不共线,这5点最多可确定多少条直线?
【即时训练】
问题 各问题研析 结果
(1) 由减法定义知,结果都与两数相减的顺序有关,故(1)是排列 (1)
(3)
(2) 由乘法定义知,结果都与两数相乘的顺序无关,故(2)不是排列 (3) 车票与始点站和终点站有关,由排列定义知(3)是排列 (4) 所选取两名同学参加座谈会,无顺序之分,故(4)不是排列 (5) 两点确定一条直线,与两点顺序无关,故(5)不是排列 解:
是否有顺序,有顺序且是从n个不同的元素中任取m(m≤n)个不同的元素的问题就是排列,否则就不是排列,
【总结提升】
判断一个问题是否为排列问题的依据
检验它是否有顺序的依据
变换元素的位置,看其结果是否有变化,有变化就是有顺序,无变化就是无顺序.
判断下列问题是否是排列问题:
(1)某班共有50名同学,现要投票选举正、副班长各一人,共有多少种可能的选举结果?
(2)从2,3,5,7,9中任取两数分别作对数的底数和指数,有多少不同对数值?
(3)从1到10十个自然数中任取两个数组成点的坐标,可得多少个不同的点的坐标?
【变式练习】
(4)从集合M={1,2,…,9}中,任取相异的两个
元素作为a,b,可以得到多少个焦点在x轴上的椭
圆方程
解: (1)是排列问题.选出的2人,担任正、副班长任意,与顺序有关,所以该问题是排列问题.
(2)是排列问题.显然对数值与底数和真数的取值的不同有关系,与顺序有关.
(3)是排列问题.任取两个数组成点的坐标,横、纵坐标的顺序不同,即为不同的坐标,与顺序有关.
(4)不是排列问题.焦点在x轴上的椭圆,方程中的a、b必有a>b,a、b的大小一定.
应用举例:
【例1】某省中学生足球赛预选赛每组有6支队,每支队都要与同组的其他队在主、客场分别比赛一场,那么每组共进行多少场比赛?
分析:每组任意2支队之间进行的一场比赛,可以看做是从该组6支队中选取2支,按“主队、客队”的顺序排成的一个排列.
解:从6支队伍中选2支,按“主队、客队”进行排列,分两步,第一步选1支做主队,有6种选法,第二步从剩下的5支队中选1支做客队,按照乘法计数原理,每组进行的比赛场次为 6×5=30.
【例2】(1)一张餐桌上有5盘不同的菜,甲、乙、丙3名同学每人从中各取1盘菜,共有多少种不同的取法?
(2)学校食堂的一个窗口共卖5种菜,甲、乙、丙3名同学每人从中选1种,共有多少种不同的选法?
分析:3名同学每人从5盘不同的菜中取1盘菜,可以看做是从这5盘菜中选取3盘,放在3个位置(给3名同学)的一个排列;而3名同学每人从食堂窗口的5种菜中选1种,每人都有5种选法,不能看成一个排列。
解:(1)可以先从这盘菜中取1盘给同学甲,然后从剩下的4盘菜中取1盘给同学乙,然最后从剩下的3盘菜中取1盘给同学丙,按乘法分步计数原理,不同的选法种数为 5×4×3=60.
(2)可以先让甲同学从5种菜中选1种,有5种选法;再让乙同学从5种菜中选1种,也有5种选法;最后让丙同学从5种菜中选1种,同样有5种选法.按乘法分步计数原理,不同的选法种数为 5×5×5=125.
【练习】
课本:P16 练习题
1.下列问题中:
(1)10本不同的书分给10名同学,每人一本;
(2)10位同学互通一次电话;
(3)10位同学互通一封信;
(4)10个没有任何三点共线的点构成的线段.
属于排列的有( )
A.1个 B.2个 C.3个 D.4个
解:(1)(3)是排列问题,(2)(4)不是排列问题.
B
2.用1,2,3,4四个数字排成三位数,并把这些三位数从小到大排成一个数列{an}.
(1)写出这个数列的前11项.
(2)这个数列共有多少项.
解:(1)111,112,113,114,121,122,123,124,
131,132,133.
(2)这个数列的项数就是用1,2,3,4排成三位数的个数,每一位都有4种排法,则共有4×4×4=64(项).
排列
按一定顺序排列
取出元素
不仅与选取的元素有关
而且与选取的元素排列顺序有关
布置作业:
1.完成课本P26 习题6.2第5,9题;
2.课时训练三。
