2020-2021学年高二下学期数学人教A版选修2-2-1.3.3函数的最大(小)值与导数 课件36张PPT
文档属性
| 名称 | 2020-2021学年高二下学期数学人教A版选修2-2-1.3.3函数的最大(小)值与导数 课件36张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 691.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览










文档简介
利用导数求函数的最值
1.函数f(x)在[a,b]上有最值的条件:如果在区间[a,b]上函数y=f(x)的图象是一条_________的曲线,那么它必有最大值和最小值.
连续不断
知识点:
2.求y=f(x)在[a,b]上的最大(小)值的步骤:
(i)求函数y=f(x)在(a,b)内的_____.
(ii)将函数y=f(x)的各极值与_______________
__________比较,其中_____的一个是最大值,
_____的一个是最小值.
极值
端点处的函数值
f(a),f(b)
最小
最大
3.极值与最值的关系
①极值反映的是函数在某一点附近的局部性质,而函数最值在整个定义域内的性质。②极值只能在定义域内取得(不包括端点),最值却可以在端点处取得。③有极值的不一定有最值,极值有可能成为最值,有最值的也未必有极值,非常数可导函数最值只要不在端点处取,则必定在极值处取.
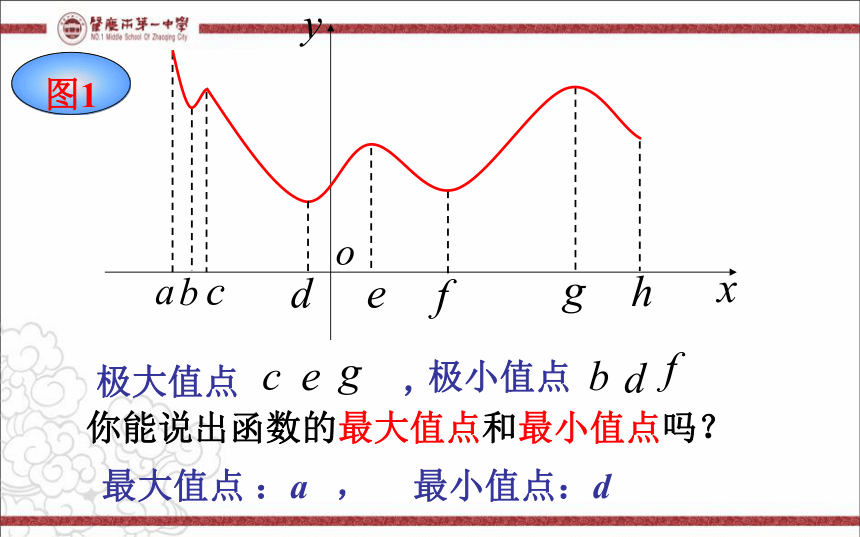
极大值点 ,
极小值点
你能说出函数的最大值点和最小值点吗?
最大值点 :a ,
最小值点:d
图1
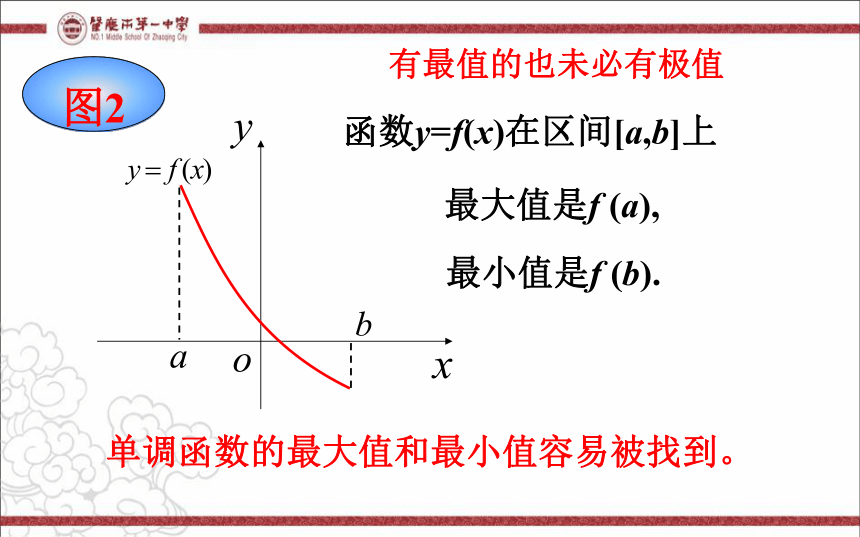
最小值是f (b).
单调函数的最大值和最小值容易被找到。
函数y=f(x)在区间[a,b]上
最大值是f (a),
图2
有最值的也未必有极值
例1、求函数f(x)=x3-12x+12在[0, 3]上的最值。
x
0
(0,2)
2
(2,3)
3
-
0
+
f(x)
12
单调递减↘
极小值为
-4
单调递增↗
3
解:f'(x)=3x2-12=0求得x=-2或x=2,所以在[0,3]上,
因此,原函数在[0, 3]上的最大值为12,最小值为-4。
题型1 求函数极值与端点值得最值
例1、求函数f(x)=x3-12x+12在[0,3]上的最值。
当x=2时, f(x)=x3-12x+12有极小值,
并且极小值为f (2)=-4.
又由于f (0)=12,f (3)=3,
所以原函数在[0, 3]上的最大值为12,最小值为-4。
解:f'(x)=3x2-12=0求得x=-2或x=2,所以在[0,3]上,
在(0,2)上,f'(x)<0,在(2,3)上,f'(x)>0,
所以当x=2时, f(x)有最小值
并且最小值为f (2)=-4.
题型1 求函数极值与端点值得最值
练习1、函数 y = x? + 3 x?-9x在 [-4 , 4 ]上的最大值为 ,最小值为 .
解: (1) 由 f ?(x)=3x? +6x-9=0,
(2) 区间[-4 , 4]端点处的函数值为 f (-4) =20 , f (4) =76
得x1=-3,x2=1
函数值为f (-3)=27, f (1)=-5
76
-5
当x变化时,y′ 、 y的变化情况如下表:
x
-4
(-4,-3)
-3
(-3,1)
1
(1,4)
4
y′
+
0
-
0
+
y
20
递增
27
递减
-5
递增
76
所以函数在[-4 , 4 ]上的最大值为 f (4) =76,最小值为 f (1)=-5
练习2.函数y=x+2cosx在区间 上的最大值是________.
【解析】y'=1-2sinx,令y'=0,
又因为x∈ ,解得
则当x∈ 时,y'>0;当x∈ 时,y'<0,
故函数y=x+2cosx在 时取最大值
题型1 求函数极值与端点值得最值
【例2】已知a,b为正实数,函数f(x)=ax3+bx+2x在[0,1]上的最大值为4,则函数f(x)在[-1,0]上的最小值为( )
题型2 含参函数的最值问题(高考热点)
【解】选A.因为函数f(x)=ax3+bx+2x,
所以f'(x)=3ax2+b+2xln2.
又因为a,b为正实数,
所以当0≤x≤1时,3ax2≥0,2xln2>0,
则f'(x)>0,即f(x)在[0,1]上为增函数,
所以f(1)最大且为a+b+2=4,即a+b=2.
又当-1≤x≤0时,3ax2≥0,2xln2>0,则f'(x)>0,
即f(x)在[-1,0]上为增函数,
所以f(-1)最小且为
所以函数f(x)在[-1,0]上的最小值为f(-1)=
【例3】已知函数f(x)=-x3+ax2-4在x=2处取得极值,若m,n∈[-1,1],则f(m)+f'(n)的最小值是( )
A.-13 B.-15 C.10 D.15
题型3 函数极值与最值的综合应用
【解】选A.求导得f'(x)=-3x2+2ax,
由函数f(x)在x=2处取得极值知f'(2)=0,
即-3×4+2a×2=0,所以a=3.
由此可得f(x)=-x3+3x2-4,f'(x)=-3x2+6x,易知f(x)在[-1,0)上单调递减,在(0,1]上单调递增,
所以当m∈[-1,1]时,f(m)min=f(0)=-4.
又因为f'(x)=-3x2+6x的图象开口向下,且对称轴为x=1,
所以当n∈[-1,1]时,f'(n)min=f'(-1)=-9.
故f(m)+f'(n)的最小值为-13.
【课后练习】
1.函数f(x)=x2-2ax+a在区间(-∞,1)上有最小值,则函
数g(x)= 在区间(1,+∞)上一定( )
A.有最小值 B.有最大值 C.是减函数 D.是增函数
2.若函数f(x)= (a>0)在[1,+∞)上的最大值
为 则a的值为( )
【解】1选D.由函数f(x)=x2-2ax+a在区间(-∞,1)上
有最小值,可得a的取值范围为a<1,
又g(x)=
则g'(x)= 易知在x∈(1,+∞)上g'(x)>0,
所以g(x)为增函数.
【解】2选D.f'(x)=
令f'(x)=0,得 或 (舍去),
(1)若 ≤1,即0f(x)max=f(1)=
解得 符合题意.
(2)若 >1,即a>1时,在 上f'(x)>0,在
上f'(x)<0,
所以f(x)max=
解得 不符合题意,综上知,
【规律小结】解决函数极值、最值问题的策略
(1)求极值、最值时,要求步骤规范,含参数时,要讨论参数的大小.
(2)求函数最值时,不可想当然地认为极值点就是最值点,要通过比较才能下结论.
(3)函数在给定闭区间上存在极值,一般要将极值与端点值进行比较才能确定最值.
【自我训练】1已知函数f(x)=x2eax,其中a≤0,e为自然对数的底数.
(1)讨论函数f(x)的单调性.
(2)求函数f(x)在区间[0,1]上的最大值.
【解析】(1)f'(x)=2xeax+x2aeax=x(ax+2)eax.
①当a=0时,由f'(x)>0得x>0,
由f'(x)<0得x<0.
故函数f(x)在(0,+∞)上单调递增,在(-∞,0)上单调递减.
②当a<0时,由f'(x)>0得
由f'(x)<0得x<0或
故函数f(x)在 上单调递增,
在(-∞,0)与 上单调递减.
(2)①当a=0时,f(x)在区间[0,1]上单调递增,其最大值
为f(1)=1.
②当-2其最大值是f(1)=ea.
③当a≤-2时, 是函数f(x)在区间[0,1]
上唯一的极大值点,也就是最大值点,
此时函数f(x)最大值是
综上得当-2当a≤-2时,f(x)在[0,1]上的最大值为
【自我训练】2、已知函数
f(x)= 的导函数
y=f'(x)的两个零点为-3和0.
(1)求f(x)的单调区间.
(2)若f(x)的极小值为-e3,求f(x)在区间[-5,+∞)上的最大值.
【解题导引】(1)求出函数f(x)的导函数,利用导函数的零点为-3和0确定函数f(x)的单调区间.
(2)由(1)知x=-3是f(x)的极小值点,依据已知条件列出关于a,b,c的方程组,求出函数f(x)的解析式,从而确定f(x)在区间[-5,+∞)上的最大值.
【规范解答】(1)f'(x)=
令g(x)=-ax2+(2a-b)x+b-c,
因为ex>0,所以y=f'(x)的零点就是g(x)=-ax2+(2a-b)x
+b-c的零点,且f'(x)与g(x)符号相同.
又因为a>0,
所以-30,即f'(x)>0,
当x<-3或x>0时,g(x)<0,即f'(x)<0,
所以f(x)的单调递增区间是(-3,0),单调递减区间是
(-∞,-3),(0,+∞).
(2)由(1)知,x=-3是f(x)的极小值点,
所以有
解得a=1,b=5,c=5,
所以f(x)=
因为f(x)的单调递增区间是(-3,0),单调递减区间是
(-∞,-3),(0,+∞),
所以f(0)=5为函数f(x)的极大值,
故f(x)在区间[-5,+∞)上的最大值取f(-5)和f(0)中的
最大者.
而f(-5)= =5e5>5=f(0),
所以函数f(x)在区间[-5,+∞)上的最大值是5e5.
【自我训练】3、已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)
在点x=1处的切线为l:3x-y+1=0,若x= 时,y=f(x)有
极值.
(1)求a,b,c的值.
(2)求y=f(x)在[-3,1]上的最大值和最小值.
【解析】(1)由f(x)=x3+ax2+bx+c,
得f'(x)=3x2+2ax+b.
当x=1时,切线l的斜率为3,可得2a+b=0,①
当x= 时,y=f(x)有极值,则
可得4a+3b+4=0,②
由①②,解得a=2,b=-4.
由于切点的横坐标为1,所以f(1)=4.
所以1+a+b+c=4,得c=5.
(2)由(1)可得f(x)=x3+2x2-4x+5,
f'(x)=3x2+4x-4.
令f'(x)=0,解得
当x变化时,f'(x),f(x)的取值及变化情况如表所示:
最小值为 最大值为13.
【自我训练】4、已知函数f(x)=
求函数f(x)在 上的最大值和最小值.
(2)因为f(x)=
f'(x)=
①若k=0,则f'(x)= 在 上恒有f'(x)<0,
所以f(x)在 上单调递减.
所以f(x)min=f(e)=
f(x)max=
②若k≠0,f'(x)=
(ⅰ)若k<0,则在 上恒有
所以f(x)在 上单调递减,
所以f(x)min=f(e)=
f(x)max=
(ⅱ)若k>0,由
得 则
所以
所以f(x)在 上单调递减.
所以f(x)min=f(e)=
f(x)max=
综上, 时,f(x)min= f(x)max=e-k-1.
1.函数f(x)在[a,b]上有最值的条件:如果在区间[a,b]上函数y=f(x)的图象是一条_________的曲线,那么它必有最大值和最小值.
连续不断
知识点:
2.求y=f(x)在[a,b]上的最大(小)值的步骤:
(i)求函数y=f(x)在(a,b)内的_____.
(ii)将函数y=f(x)的各极值与_______________
__________比较,其中_____的一个是最大值,
_____的一个是最小值.
极值
端点处的函数值
f(a),f(b)
最小
最大
3.极值与最值的关系
①极值反映的是函数在某一点附近的局部性质,而函数最值在整个定义域内的性质。②极值只能在定义域内取得(不包括端点),最值却可以在端点处取得。③有极值的不一定有最值,极值有可能成为最值,有最值的也未必有极值,非常数可导函数最值只要不在端点处取,则必定在极值处取.
极大值点 ,
极小值点
你能说出函数的最大值点和最小值点吗?
最大值点 :a ,
最小值点:d
图1
最小值是f (b).
单调函数的最大值和最小值容易被找到。
函数y=f(x)在区间[a,b]上
最大值是f (a),
图2
有最值的也未必有极值
例1、求函数f(x)=x3-12x+12在[0, 3]上的最值。
x
0
(0,2)
2
(2,3)
3
-
0
+
f(x)
12
单调递减↘
极小值为
-4
单调递增↗
3
解:f'(x)=3x2-12=0求得x=-2或x=2,所以在[0,3]上,
因此,原函数在[0, 3]上的最大值为12,最小值为-4。
题型1 求函数极值与端点值得最值
例1、求函数f(x)=x3-12x+12在[0,3]上的最值。
当x=2时, f(x)=x3-12x+12有极小值,
并且极小值为f (2)=-4.
又由于f (0)=12,f (3)=3,
所以原函数在[0, 3]上的最大值为12,最小值为-4。
解:f'(x)=3x2-12=0求得x=-2或x=2,所以在[0,3]上,
在(0,2)上,f'(x)<0,在(2,3)上,f'(x)>0,
所以当x=2时, f(x)有最小值
并且最小值为f (2)=-4.
题型1 求函数极值与端点值得最值
练习1、函数 y = x? + 3 x?-9x在 [-4 , 4 ]上的最大值为 ,最小值为 .
解: (1) 由 f ?(x)=3x? +6x-9=0,
(2) 区间[-4 , 4]端点处的函数值为 f (-4) =20 , f (4) =76
得x1=-3,x2=1
函数值为f (-3)=27, f (1)=-5
76
-5
当x变化时,y′ 、 y的变化情况如下表:
x
-4
(-4,-3)
-3
(-3,1)
1
(1,4)
4
y′
+
0
-
0
+
y
20
递增
27
递减
-5
递增
76
所以函数在[-4 , 4 ]上的最大值为 f (4) =76,最小值为 f (1)=-5
练习2.函数y=x+2cosx在区间 上的最大值是________.
【解析】y'=1-2sinx,令y'=0,
又因为x∈ ,解得
则当x∈ 时,y'>0;当x∈ 时,y'<0,
故函数y=x+2cosx在 时取最大值
题型1 求函数极值与端点值得最值
【例2】已知a,b为正实数,函数f(x)=ax3+bx+2x在[0,1]上的最大值为4,则函数f(x)在[-1,0]上的最小值为( )
题型2 含参函数的最值问题(高考热点)
【解】选A.因为函数f(x)=ax3+bx+2x,
所以f'(x)=3ax2+b+2xln2.
又因为a,b为正实数,
所以当0≤x≤1时,3ax2≥0,2xln2>0,
则f'(x)>0,即f(x)在[0,1]上为增函数,
所以f(1)最大且为a+b+2=4,即a+b=2.
又当-1≤x≤0时,3ax2≥0,2xln2>0,则f'(x)>0,
即f(x)在[-1,0]上为增函数,
所以f(-1)最小且为
所以函数f(x)在[-1,0]上的最小值为f(-1)=
【例3】已知函数f(x)=-x3+ax2-4在x=2处取得极值,若m,n∈[-1,1],则f(m)+f'(n)的最小值是( )
A.-13 B.-15 C.10 D.15
题型3 函数极值与最值的综合应用
【解】选A.求导得f'(x)=-3x2+2ax,
由函数f(x)在x=2处取得极值知f'(2)=0,
即-3×4+2a×2=0,所以a=3.
由此可得f(x)=-x3+3x2-4,f'(x)=-3x2+6x,易知f(x)在[-1,0)上单调递减,在(0,1]上单调递增,
所以当m∈[-1,1]时,f(m)min=f(0)=-4.
又因为f'(x)=-3x2+6x的图象开口向下,且对称轴为x=1,
所以当n∈[-1,1]时,f'(n)min=f'(-1)=-9.
故f(m)+f'(n)的最小值为-13.
【课后练习】
1.函数f(x)=x2-2ax+a在区间(-∞,1)上有最小值,则函
数g(x)= 在区间(1,+∞)上一定( )
A.有最小值 B.有最大值 C.是减函数 D.是增函数
2.若函数f(x)= (a>0)在[1,+∞)上的最大值
为 则a的值为( )
【解】1选D.由函数f(x)=x2-2ax+a在区间(-∞,1)上
有最小值,可得a的取值范围为a<1,
又g(x)=
则g'(x)= 易知在x∈(1,+∞)上g'(x)>0,
所以g(x)为增函数.
【解】2选D.f'(x)=
令f'(x)=0,得 或 (舍去),
(1)若 ≤1,即0
解得 符合题意.
(2)若 >1,即a>1时,在 上f'(x)>0,在
上f'(x)<0,
所以f(x)max=
解得 不符合题意,综上知,
【规律小结】解决函数极值、最值问题的策略
(1)求极值、最值时,要求步骤规范,含参数时,要讨论参数的大小.
(2)求函数最值时,不可想当然地认为极值点就是最值点,要通过比较才能下结论.
(3)函数在给定闭区间上存在极值,一般要将极值与端点值进行比较才能确定最值.
【自我训练】1已知函数f(x)=x2eax,其中a≤0,e为自然对数的底数.
(1)讨论函数f(x)的单调性.
(2)求函数f(x)在区间[0,1]上的最大值.
【解析】(1)f'(x)=2xeax+x2aeax=x(ax+2)eax.
①当a=0时,由f'(x)>0得x>0,
由f'(x)<0得x<0.
故函数f(x)在(0,+∞)上单调递增,在(-∞,0)上单调递减.
②当a<0时,由f'(x)>0得
由f'(x)<0得x<0或
故函数f(x)在 上单调递增,
在(-∞,0)与 上单调递减.
(2)①当a=0时,f(x)在区间[0,1]上单调递增,其最大值
为f(1)=1.
②当-2
③当a≤-2时, 是函数f(x)在区间[0,1]
上唯一的极大值点,也就是最大值点,
此时函数f(x)最大值是
综上得当-2
【自我训练】2、已知函数
f(x)= 的导函数
y=f'(x)的两个零点为-3和0.
(1)求f(x)的单调区间.
(2)若f(x)的极小值为-e3,求f(x)在区间[-5,+∞)上的最大值.
【解题导引】(1)求出函数f(x)的导函数,利用导函数的零点为-3和0确定函数f(x)的单调区间.
(2)由(1)知x=-3是f(x)的极小值点,依据已知条件列出关于a,b,c的方程组,求出函数f(x)的解析式,从而确定f(x)在区间[-5,+∞)上的最大值.
【规范解答】(1)f'(x)=
令g(x)=-ax2+(2a-b)x+b-c,
因为ex>0,所以y=f'(x)的零点就是g(x)=-ax2+(2a-b)x
+b-c的零点,且f'(x)与g(x)符号相同.
又因为a>0,
所以-3
当x<-3或x>0时,g(x)<0,即f'(x)<0,
所以f(x)的单调递增区间是(-3,0),单调递减区间是
(-∞,-3),(0,+∞).
(2)由(1)知,x=-3是f(x)的极小值点,
所以有
解得a=1,b=5,c=5,
所以f(x)=
因为f(x)的单调递增区间是(-3,0),单调递减区间是
(-∞,-3),(0,+∞),
所以f(0)=5为函数f(x)的极大值,
故f(x)在区间[-5,+∞)上的最大值取f(-5)和f(0)中的
最大者.
而f(-5)= =5e5>5=f(0),
所以函数f(x)在区间[-5,+∞)上的最大值是5e5.
【自我训练】3、已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)
在点x=1处的切线为l:3x-y+1=0,若x= 时,y=f(x)有
极值.
(1)求a,b,c的值.
(2)求y=f(x)在[-3,1]上的最大值和最小值.
【解析】(1)由f(x)=x3+ax2+bx+c,
得f'(x)=3x2+2ax+b.
当x=1时,切线l的斜率为3,可得2a+b=0,①
当x= 时,y=f(x)有极值,则
可得4a+3b+4=0,②
由①②,解得a=2,b=-4.
由于切点的横坐标为1,所以f(1)=4.
所以1+a+b+c=4,得c=5.
(2)由(1)可得f(x)=x3+2x2-4x+5,
f'(x)=3x2+4x-4.
令f'(x)=0,解得
当x变化时,f'(x),f(x)的取值及变化情况如表所示:
最小值为 最大值为13.
【自我训练】4、已知函数f(x)=
求函数f(x)在 上的最大值和最小值.
(2)因为f(x)=
f'(x)=
①若k=0,则f'(x)= 在 上恒有f'(x)<0,
所以f(x)在 上单调递减.
所以f(x)min=f(e)=
f(x)max=
②若k≠0,f'(x)=
(ⅰ)若k<0,则在 上恒有
所以f(x)在 上单调递减,
所以f(x)min=f(e)=
f(x)max=
(ⅱ)若k>0,由
得 则
所以
所以f(x)在 上单调递减.
所以f(x)min=f(e)=
f(x)max=
综上, 时,f(x)min= f(x)max=e-k-1.
