陕西省商洛市2021届高三上学期期末教学质量检测理科数学试题 Word版含解析
文档属性
| 名称 | 陕西省商洛市2021届高三上学期期末教学质量检测理科数学试题 Word版含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 704.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 15:24:46 | ||
图片预览




文档简介
1219200010452100商洛市2020~2021学年度第一学期期末教学质量检测
高三数学试卷(理科)
考生注意:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.
2.请将各题答案填写在答题卡上.
3.本试卷主要考试内容:高考全部内容.
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合false,false,则false
A.false B.false
Cfalse D.false
2.复数false的虚部为
A.false B.false C.false D.false
3.双曲线false的渐近线方程为
A.false B.false C.false D.false
4.若false,false,则false
A.false B.false C.false D.false
5.记false为等差数列false的前n项和,已知false,则数列false的公差为
A.4 B.2 C.1 D.false
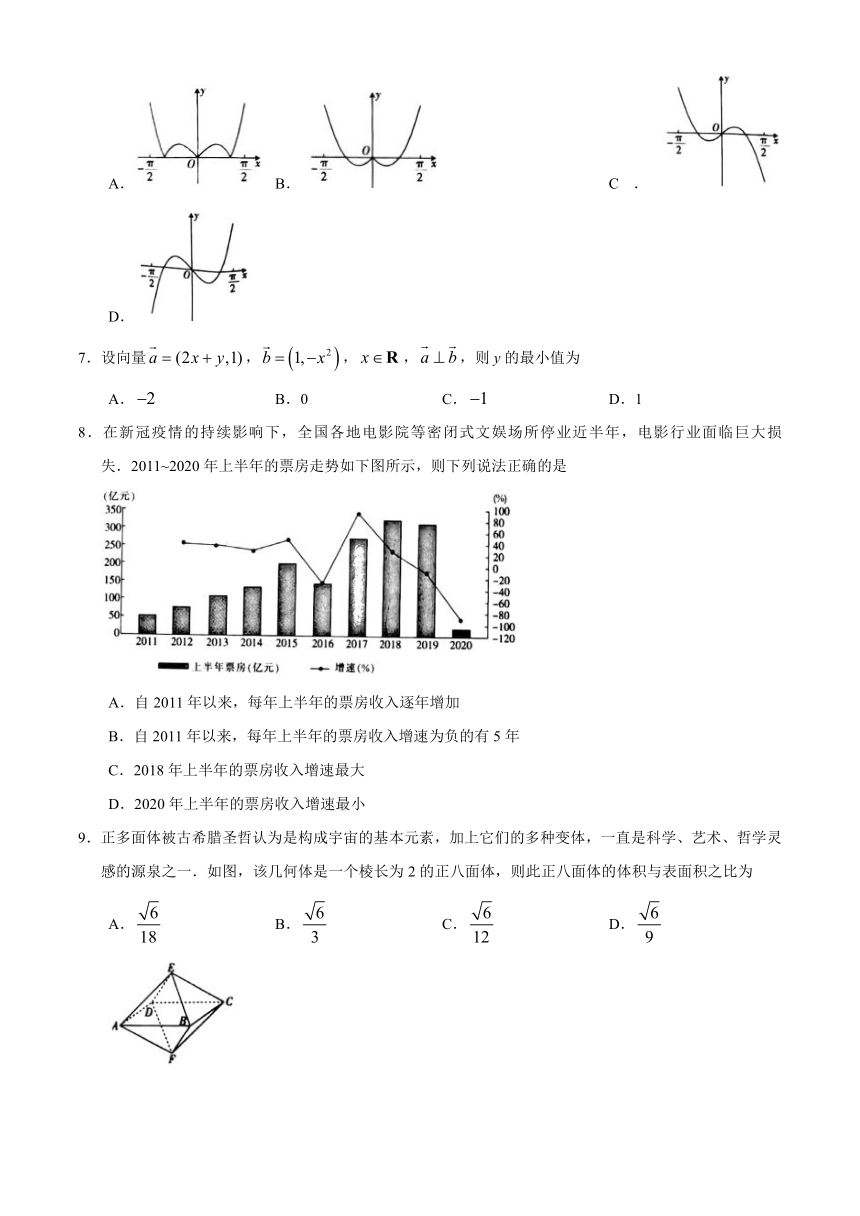
6.函数false在false上的图象大致为
A. B. C. D.
7.设向量false,false,false,false,则y的最小值为
A.false B.0 C.false D.1
8.在新冠疫情的持续影响下,全国各地电影院等密闭式文娱场所停业近半年,电影行业面临巨大损失.2011~2020年上半年的票房走势如下图所示,则下列说法正确的是
A.自2011年以来,每年上半年的票房收入逐年增加
B.自2011年以来,每年上半年的票房收入增速为负的有5年
C.2018年上半年的票房收入增速最大
D.2020年上半年的票房收入增速最小
9.正多面体被古希腊圣哲认为是构成宇宙的基本元素,加上它们的多种变体,一直是科学、艺术、哲学灵感的源泉之一.如图,该几何体是一个棱长为2的正八面体,则此正八面体的体积与表面积之比为
A.false B.false C.false D.false
10.已知等比数列false的前n项和为false,若false,false,则false
A.9 B.10 C.12 D.17
11.设直四棱柱false的每个顶点都在球O的球面上,底面ABCD为平行四边形,false,侧面false的面积为6,则球O表面积的最小值为
A.false B.false C.false D.false
12.已知奇函数false的定义域为R,且对任意false,false恒成立,则不等式组false的解集是
A.false B.false C.false D.false
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.若x,y满足约束条件false则false的最大值为________.
14.false的展开式中的常数项为________.
15.已知椭圆C的离心率为false,短半轴长为false,则椭圆C的焦距为________.
16.关于函数false有如下四个命题:
①false在false上的值域为false;
②false的图象不可能经过坐标原点;
③若false的最小正周期为2,则false;
④若false,则false的最小值为false.
其中所有真命题的序号是________.
三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)
a,b,c分别为false内角A,B,C的对边.已知false,false.
(1)求false;
(2)若false的周长为false,求false的面积(结果用小数表示,取false).
18.(12分)
我国在芯片领域的短板有光刻机和光刻胶,某风投公司准备投资芯片领域.若投资光刻机项目,据预期,每年的收益率为false的概率为p,收益率为false的概率为false;若投资光刻胶项目,据预期,每年的收益率为false的概率为false,收益率为false的概率为0.1,收益率为零的概率为0.5.
(1)已知投资以上两个项目,获利的期望是一样的,请你为该风投公司选择一个合理的项目,并说明理由;
(2)若该风投公司准备对以上你认为比较合理的的项目进行投资,4年累计投资数据如下表:
年份x
2016
2017
2018
2019
false
1
2
3
4
累计投资金额y(单位:亿元)
2
3
5
6
请根据上表提供的数据,用最小二乘法求出y关于false的线性回归方程false,并预测到哪一年年末,该公司在芯片领域的投资收益预期能达到0.75亿元.
附:收益false收入的资金false获利期望;线性回归方程false中,false,false.
19.(12分)
如图,已知三棱柱false是底面边长为2,高为4的正三棱柱,点E在棱false上,且false.
(1)当false为何值时,平面false平面false?说明你的理由.
(2)若false,求二面角false的余弦值.
20.(12分)
已知函数false.
(1)讨论函数false的单调性;
(2)若不等式false对false恒成立,求a的取值范围.
21.(12分)
抛物线C:false的焦点为F,过F且垂直于y轴的直线交抛物线C于M,N两点,O为原点,false的面积为2.
(1)求抛物线C的方程.
(2)P为直线l:false上一个动点,过点P作抛物线的切线,切点分别为A,B,过点P作AB的垂线,垂足为H,是否存在实数false,使点P在直线l上移动时,垂足H恒为定点?若不存在,说明理由;若存在,求出false的值,并求定点H的坐标.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
22.[选修4-4:坐标系与参数方程](10分)
在直角坐标系xOy中,直线l的参数方程为false(t为参数),以坐标原点为极点,以x轴的非负半轴为极轴,建立极坐标系,曲线C的极坐标方程为false,已知直线l与曲线C交于不同的两点M,N.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设false,求false的值.
23.[选修4-5:不等式选讲](10分)
设函数false.
(1)求不等式false的解集;
(2)若false的最小值是m,且false,求false的最小值.
商洛市2020~2021学年度第一学期期末教学质量检测
高三数学试卷参考答案(理科)
1.C 因为false,false,
所以false.
2.B false,则z的虚部为false.
3.A 因为false,所以false,
故双曲线的渐近线方程为false.
4.D 因为false,
false,
所以false,
则false.
5.A 设d为数列false的公差,因为false,
所以false,则false.
6.B 因为false,所以false为偶函数,其图象关于y轴对称,故排除C与D.
因为false,所以排除A,故选B.
7.C 因为false,所以false,
则false.
8.D 由图易知自2011年以来,每年上半年的票房收入相比前一年有增有减,增速为负的有3年,故A,B错误;
2017年上半年的票房收入增速最大,故C错误;
2020年上半年的票房收入增速最小,故D正确.
9.D 正八面体的上、下结构是两个相同的正四棱锥,由勾股定理求得斜高,再由棱锥的体积公式即可求解.
由边长为2,可得正八面体上半部分的斜高为false,高为false,
则其体积为false,其表面积为false
所以此正八面体的体积与表面积之比为false.
10.B 设等比数列false的公比为q,
因为false,所以false,
则false.
11.A 因为底面ABCD为平行四边形,且球O是直四棱柱false的外接球,
所以底面ABCD必为矩形,从而四棱false为长方体.
设false,false,则false,false,
所以球O的表面积
false,
当且仅当false,即false时,等号成立,
故球O表面积的最小值为false.
12.C 设false,则false,
则false在R上单调递增.
因为false是定义域为R的奇函数,所以false,则false.
不等式组false
等价于false即false,
则false,解得false.
13.15 作出可行域(图略),由图可知,当直线false经过点false时,z取得最大值,且最大值为15.
14.false
展开式的通项为false,令false,得false,
所以展开式中的常数项为false.
15.4 设椭圆C的长半轴长为a,短半轴长为b,半焦距为c,
则false解得false,
所以椭圆C的焦距为4.
16.①②③④
若false,则false,false,所以①为真命题.
因为false 所以false的图象不可能经过坐标原点,所以②为真命题.
若false的最小正周期为2,则false,
则false,所以③是真命题.
若false,则false的图象关于直线false对称,
则false,所以false,
因为false,所以false的最小值为false,所以④为真命题.
17.解:(1)因为false,
所以false.
(2)因为false,所以false.
由余弦定理得false,则false.
因为false的周长为false,
所以false,解得false.
所以false的面积为false.
因为false,所以false的面积为3.8.
18.解:(1)若投资光刻机项目,设收益率为false,则false的分布列为
false
0.3
false
P
p
false
所以false.
若投资光刻胶项目,设收益率为false,则false的分布列为
false
0.3
false
0
P
0.4
0.1
0.5
所以false.
因为投资以上两个项目,获利的期望是一样的,
所以false,所以false.
因为false,
false,
所以false,false,
这说明虽然光刻机项目和光刻胶项目获利相等,但光刻胶项目更稳妥.
综上所述,建议该风投公司投资光刻胶项目.
(2)false,false,
false,false,
则false,false,
故线性回归方程为false.
设该公司在芯片领域的投资收益为Y,则false,
解得false,故在2020年年末该投资公司在芯片领域的投资收益可以超过0.75亿元.
19.解:(1)当false时,平面false平面false.
证明如下:
如图,当false时,点E为棱false的中点,
记false与false相交于点D,记线段AC的中点为O,
易证DO与EB平行且相等,
则四边形EDOB为平行四边形,则false.
因为false为正三角形,则false,
易知false,false,
则false平面false,
则false平面false,因为false平面false,
所以平面false平面false.
(2)以O为坐标原点,以false的方向为x轴的正方向,建立空间直角坐标系false,如图所示,
则false,false,false,false,
则false,false,false.
设平面AEC的法向量为false,
则false即false
令false,得false.
设平面false的法向量为false,
则false即false
令false,得false.
false,
由图可知二面角false为钝角,
故二面角false的余弦值为false.
20.解:(1)函数false的定义域为false,且false.
若false,则当false时,false,函数false在false上单调递增;
当false时,false,函数false在false上单调递减.
若false,false,函数false在false上单调递减.
(2)不等式false在false上恒成立,即false恒成立,
设false,false,
令false,则false.
①当false时,false恒成立,
所以false单调递增,所以false,
即false符合题意;
②当false时,false恒成立,所以false单调递增,
又因为false,false,
所以存在false,使得false,且当false时,
false,即false在false上单调递减,
所以false,即false不符合题意.
综上,a的取值范围为false.
21.解:(1)由题意得,点M,N的纵坐标均为false,由false,
解得false,则false.
由false,
解得false,故抛物线C的方程为false.
(2)设false,false,false,
直线AP的方程为false.
将抛物线方程变形为false,则false,所以false,
所以AP的方程为false.
因为false,所以直线AP的方程为false,
把false代入AP的方程得false.
同理可得false.
构造直线方程为false,易知A,B两点均在该直线上,
所以直线AB的方程为false,
故AB恒过点false.
因为false,所以可设PH方程为false,
化简得false,
所以PH恒过点false.
当false,即false时,AB与PH均恒过false,
故存在这样的false,当false时,H的坐标为false.
22.解:(1)由题意可得直线l的普通方程为false.
曲线C的直角坐标方程为false,
即false.
(2)直线l的参数方程可化为false(false为参数).
将直线l的参数方程代入曲线C的直角坐标方程,
整理得false,则false,false,
故false.
23.解:(1)当false时,false,解得false;
当false时,false,解得false;
当false时,false,解得false.
综上,不等式false的解集为false.
(2)由(1)可知当false时,false,
即false,则false.
因为false
所以false,
即false(当且仅当false时等号成立).
故false的最小值为false.
高三数学试卷(理科)
考生注意:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.
2.请将各题答案填写在答题卡上.
3.本试卷主要考试内容:高考全部内容.
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合false,false,则false
A.false B.false
Cfalse D.false
2.复数false的虚部为
A.false B.false C.false D.false
3.双曲线false的渐近线方程为
A.false B.false C.false D.false
4.若false,false,则false
A.false B.false C.false D.false
5.记false为等差数列false的前n项和,已知false,则数列false的公差为
A.4 B.2 C.1 D.false
6.函数false在false上的图象大致为
A. B. C. D.
7.设向量false,false,false,false,则y的最小值为
A.false B.0 C.false D.1
8.在新冠疫情的持续影响下,全国各地电影院等密闭式文娱场所停业近半年,电影行业面临巨大损失.2011~2020年上半年的票房走势如下图所示,则下列说法正确的是
A.自2011年以来,每年上半年的票房收入逐年增加
B.自2011年以来,每年上半年的票房收入增速为负的有5年
C.2018年上半年的票房收入增速最大
D.2020年上半年的票房收入增速最小
9.正多面体被古希腊圣哲认为是构成宇宙的基本元素,加上它们的多种变体,一直是科学、艺术、哲学灵感的源泉之一.如图,该几何体是一个棱长为2的正八面体,则此正八面体的体积与表面积之比为
A.false B.false C.false D.false
10.已知等比数列false的前n项和为false,若false,false,则false
A.9 B.10 C.12 D.17
11.设直四棱柱false的每个顶点都在球O的球面上,底面ABCD为平行四边形,false,侧面false的面积为6,则球O表面积的最小值为
A.false B.false C.false D.false
12.已知奇函数false的定义域为R,且对任意false,false恒成立,则不等式组false的解集是
A.false B.false C.false D.false
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.若x,y满足约束条件false则false的最大值为________.
14.false的展开式中的常数项为________.
15.已知椭圆C的离心率为false,短半轴长为false,则椭圆C的焦距为________.
16.关于函数false有如下四个命题:
①false在false上的值域为false;
②false的图象不可能经过坐标原点;
③若false的最小正周期为2,则false;
④若false,则false的最小值为false.
其中所有真命题的序号是________.
三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)
a,b,c分别为false内角A,B,C的对边.已知false,false.
(1)求false;
(2)若false的周长为false,求false的面积(结果用小数表示,取false).
18.(12分)
我国在芯片领域的短板有光刻机和光刻胶,某风投公司准备投资芯片领域.若投资光刻机项目,据预期,每年的收益率为false的概率为p,收益率为false的概率为false;若投资光刻胶项目,据预期,每年的收益率为false的概率为false,收益率为false的概率为0.1,收益率为零的概率为0.5.
(1)已知投资以上两个项目,获利的期望是一样的,请你为该风投公司选择一个合理的项目,并说明理由;
(2)若该风投公司准备对以上你认为比较合理的的项目进行投资,4年累计投资数据如下表:
年份x
2016
2017
2018
2019
false
1
2
3
4
累计投资金额y(单位:亿元)
2
3
5
6
请根据上表提供的数据,用最小二乘法求出y关于false的线性回归方程false,并预测到哪一年年末,该公司在芯片领域的投资收益预期能达到0.75亿元.
附:收益false收入的资金false获利期望;线性回归方程false中,false,false.
19.(12分)
如图,已知三棱柱false是底面边长为2,高为4的正三棱柱,点E在棱false上,且false.
(1)当false为何值时,平面false平面false?说明你的理由.
(2)若false,求二面角false的余弦值.
20.(12分)
已知函数false.
(1)讨论函数false的单调性;
(2)若不等式false对false恒成立,求a的取值范围.
21.(12分)
抛物线C:false的焦点为F,过F且垂直于y轴的直线交抛物线C于M,N两点,O为原点,false的面积为2.
(1)求抛物线C的方程.
(2)P为直线l:false上一个动点,过点P作抛物线的切线,切点分别为A,B,过点P作AB的垂线,垂足为H,是否存在实数false,使点P在直线l上移动时,垂足H恒为定点?若不存在,说明理由;若存在,求出false的值,并求定点H的坐标.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
22.[选修4-4:坐标系与参数方程](10分)
在直角坐标系xOy中,直线l的参数方程为false(t为参数),以坐标原点为极点,以x轴的非负半轴为极轴,建立极坐标系,曲线C的极坐标方程为false,已知直线l与曲线C交于不同的两点M,N.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设false,求false的值.
23.[选修4-5:不等式选讲](10分)
设函数false.
(1)求不等式false的解集;
(2)若false的最小值是m,且false,求false的最小值.
商洛市2020~2021学年度第一学期期末教学质量检测
高三数学试卷参考答案(理科)
1.C 因为false,false,
所以false.
2.B false,则z的虚部为false.
3.A 因为false,所以false,
故双曲线的渐近线方程为false.
4.D 因为false,
false,
所以false,
则false.
5.A 设d为数列false的公差,因为false,
所以false,则false.
6.B 因为false,所以false为偶函数,其图象关于y轴对称,故排除C与D.
因为false,所以排除A,故选B.
7.C 因为false,所以false,
则false.
8.D 由图易知自2011年以来,每年上半年的票房收入相比前一年有增有减,增速为负的有3年,故A,B错误;
2017年上半年的票房收入增速最大,故C错误;
2020年上半年的票房收入增速最小,故D正确.
9.D 正八面体的上、下结构是两个相同的正四棱锥,由勾股定理求得斜高,再由棱锥的体积公式即可求解.
由边长为2,可得正八面体上半部分的斜高为false,高为false,
则其体积为false,其表面积为false
所以此正八面体的体积与表面积之比为false.
10.B 设等比数列false的公比为q,
因为false,所以false,
则false.
11.A 因为底面ABCD为平行四边形,且球O是直四棱柱false的外接球,
所以底面ABCD必为矩形,从而四棱false为长方体.
设false,false,则false,false,
所以球O的表面积
false,
当且仅当false,即false时,等号成立,
故球O表面积的最小值为false.
12.C 设false,则false,
则false在R上单调递增.
因为false是定义域为R的奇函数,所以false,则false.
不等式组false
等价于false即false,
则false,解得false.
13.15 作出可行域(图略),由图可知,当直线false经过点false时,z取得最大值,且最大值为15.
14.false
展开式的通项为false,令false,得false,
所以展开式中的常数项为false.
15.4 设椭圆C的长半轴长为a,短半轴长为b,半焦距为c,
则false解得false,
所以椭圆C的焦距为4.
16.①②③④
若false,则false,false,所以①为真命题.
因为false 所以false的图象不可能经过坐标原点,所以②为真命题.
若false的最小正周期为2,则false,
则false,所以③是真命题.
若false,则false的图象关于直线false对称,
则false,所以false,
因为false,所以false的最小值为false,所以④为真命题.
17.解:(1)因为false,
所以false.
(2)因为false,所以false.
由余弦定理得false,则false.
因为false的周长为false,
所以false,解得false.
所以false的面积为false.
因为false,所以false的面积为3.8.
18.解:(1)若投资光刻机项目,设收益率为false,则false的分布列为
false
0.3
false
P
p
false
所以false.
若投资光刻胶项目,设收益率为false,则false的分布列为
false
0.3
false
0
P
0.4
0.1
0.5
所以false.
因为投资以上两个项目,获利的期望是一样的,
所以false,所以false.
因为false,
false,
所以false,false,
这说明虽然光刻机项目和光刻胶项目获利相等,但光刻胶项目更稳妥.
综上所述,建议该风投公司投资光刻胶项目.
(2)false,false,
false,false,
则false,false,
故线性回归方程为false.
设该公司在芯片领域的投资收益为Y,则false,
解得false,故在2020年年末该投资公司在芯片领域的投资收益可以超过0.75亿元.
19.解:(1)当false时,平面false平面false.
证明如下:
如图,当false时,点E为棱false的中点,
记false与false相交于点D,记线段AC的中点为O,
易证DO与EB平行且相等,
则四边形EDOB为平行四边形,则false.
因为false为正三角形,则false,
易知false,false,
则false平面false,
则false平面false,因为false平面false,
所以平面false平面false.
(2)以O为坐标原点,以false的方向为x轴的正方向,建立空间直角坐标系false,如图所示,
则false,false,false,false,
则false,false,false.
设平面AEC的法向量为false,
则false即false
令false,得false.
设平面false的法向量为false,
则false即false
令false,得false.
false,
由图可知二面角false为钝角,
故二面角false的余弦值为false.
20.解:(1)函数false的定义域为false,且false.
若false,则当false时,false,函数false在false上单调递增;
当false时,false,函数false在false上单调递减.
若false,false,函数false在false上单调递减.
(2)不等式false在false上恒成立,即false恒成立,
设false,false,
令false,则false.
①当false时,false恒成立,
所以false单调递增,所以false,
即false符合题意;
②当false时,false恒成立,所以false单调递增,
又因为false,false,
所以存在false,使得false,且当false时,
false,即false在false上单调递减,
所以false,即false不符合题意.
综上,a的取值范围为false.
21.解:(1)由题意得,点M,N的纵坐标均为false,由false,
解得false,则false.
由false,
解得false,故抛物线C的方程为false.
(2)设false,false,false,
直线AP的方程为false.
将抛物线方程变形为false,则false,所以false,
所以AP的方程为false.
因为false,所以直线AP的方程为false,
把false代入AP的方程得false.
同理可得false.
构造直线方程为false,易知A,B两点均在该直线上,
所以直线AB的方程为false,
故AB恒过点false.
因为false,所以可设PH方程为false,
化简得false,
所以PH恒过点false.
当false,即false时,AB与PH均恒过false,
故存在这样的false,当false时,H的坐标为false.
22.解:(1)由题意可得直线l的普通方程为false.
曲线C的直角坐标方程为false,
即false.
(2)直线l的参数方程可化为false(false为参数).
将直线l的参数方程代入曲线C的直角坐标方程,
整理得false,则false,false,
故false.
23.解:(1)当false时,false,解得false;
当false时,false,解得false;
当false时,false,解得false.
综上,不等式false的解集为false.
(2)由(1)可知当false时,false,
即false,则false.
因为false
所以false,
即false(当且仅当false时等号成立).
故false的最小值为false.
同课章节目录
