陕西省咸阳市2020-2021学年高一上学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 陕西省咸阳市2020-2021学年高一上学期期末考试数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 1017.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 15:28:17 | ||
图片预览



文档简介
咸阳市2020-2021学年度第一学期期末教学质量检测
高一数学试题
注意事项:
1.本试题共4页,满分150分,时间120分钟;
2.答卷前,考生须准确填写自己的姓名、准考证号,并认真核准条形码上的姓名、准号;
3.第Ⅰ卷选择题必须使用2B铅笔填涂,第Ⅱ卷非选择题必须使用0.5毫米黑色墨水签字笔书写,涂写要工整、清晰;
4.考试结束后,监考员将答题卡按顺序收回,装袋整理;试题卷不回收.
第Ⅰ卷(选择题共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 已知集合,,则( )
A. B. C. D.
2. 已知函数,则( )
A. B. C. D.
3. 圆与圆的位置关系为( )
A. 内切 B. 外切 C. 相交 D. 相离
4. 如图是一个几何体的三视图,它对应的几何体的名称是( )
A. 棱台 B. 圆台 C. 圆柱 D. 圆锥
5. 在直三棱柱的棱所在直线中,与直线异面的直线条数为( )
A. B. C. D.
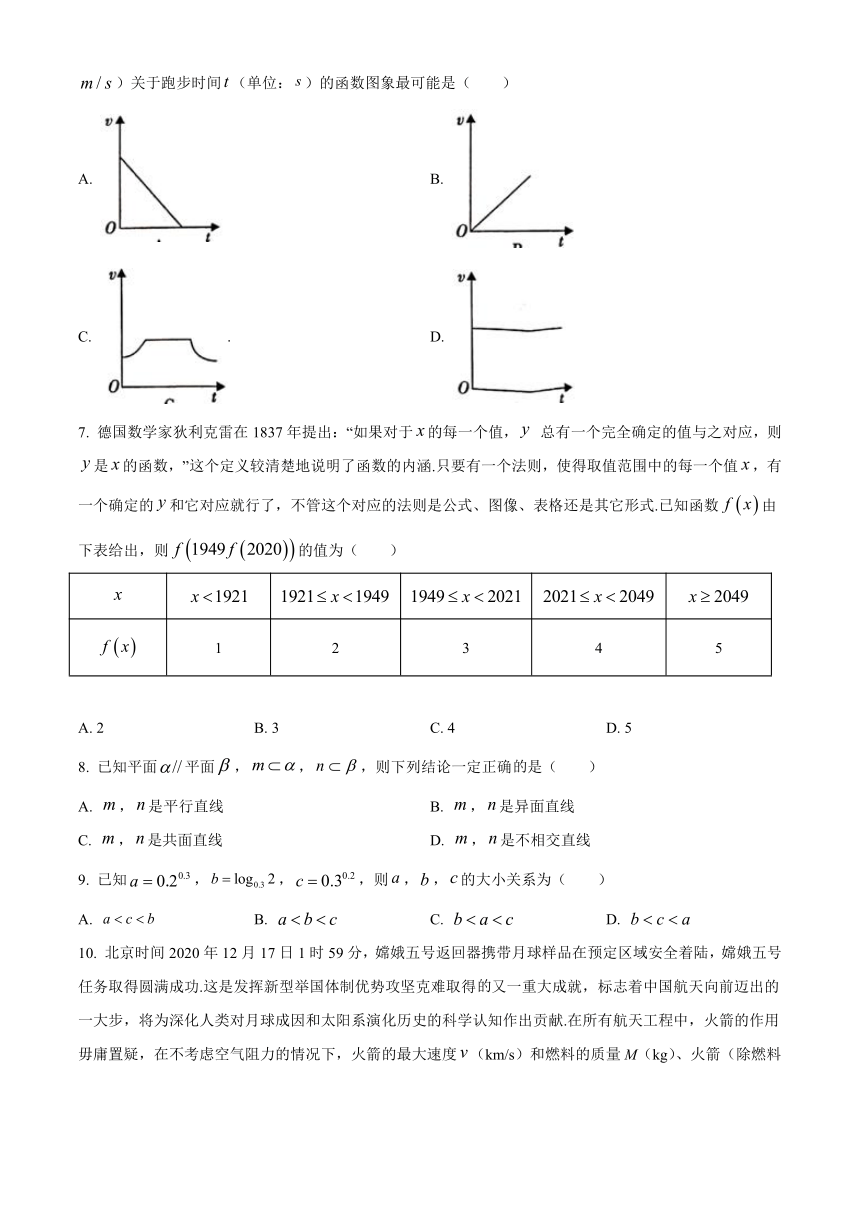
6. 某学校高中部举行秋季田径运动会,甲、乙、丙、丁位同学代表高一(1)班参加男子组米接力跑比赛,甲同学负责跑第二棒.在比赛中,从甲接到接力棒到甲送出接力棒,甲同学的跑步速率(单位:)关于跑步时间(单位:)的函数图象最可能是( )
A. B.
C. . D.
7. 德国数学家狄利克雷在1837年提出:“如果对于的每一个值, 总有一个完全确定的值与之对应,则是的函数,”这个定义较清楚地说明了函数的内涵.只要有一个法则,使得取值范围中的每一个值,有一个确定的和它对应就行了,不管这个对应的法则是公式、图像、表格还是其它形式.已知函数由下表给出,则的值为( )
1 2 3 4 5
A. 2 B. 3 C. 4 D. 5
8. 已知平面平面,,,则下列结论一定正确是( )
A. ,是平行直线 B. ,是异面直线
C. ,是共面直线 D. ,是不相交直线
9. 已知,,,则,,的大小关系为( )
A. B. C. D.
10. 北京时间2020年12月17日1时59分,嫦娥五号返回器携带月球样品在预定区域安全着陆,嫦娥五号任务取得圆满成功.这是发挥新型举国体制优势攻坚克难取得又一重大成就,标志着中国航天向前迈出的一大步,将为深化人类对月球成因和太阳系演化历史的科学认知作出贡献.在所有航天工程中,火箭的作用毋庸置疑,在不考虑空气阻力的情况下,火箭的最大速度(km/s)和燃料的质量M(kg)、火箭(除燃料外)的质量m(kg)的函数关系是.按照这个规律,若火箭的最大速度可达到第二宇宙速度11.2km/s,则火箭的燃料质量M与火箭质量m之比约为( )
(参考数据:)
A. 0.0044 B. 2.0056 C. 1.0056 D. 0.0056
11. 设点,,若直线与线段有交点,则实数的取值范围是( )
A. B.
C. D.
12. 在数学课堂上,张老师给出一个定义在上的函数,甲、乙、丙、丁四位同学各说出了这个函数的一条性质:
甲:在上函数单调递减;
乙:在上函数单调递增;
丙:函数的图像关于直线对称;
丁:不是函数的最小值.
张老师说:你们四位同学中恰好有三个人说的正确,那么,你认为说法错误的同学是( )
A. 甲 B. 乙 C. 丙 D. 丁
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13. 函数的定义域为______.
14. 已知,直线的倾斜角为,则直线的倾斜角为______.
15. 张衡(78年~139年)是中国东汉时期杰出的天文学家、数学家、发明家、地理学家、文学家,他的数学著作有《算罔论》.张衡给立方体定名为质,给球体定名为浑.他研究过球的外切立方体体积和内接立方体体积,研究过球的体积,其中还定圆周率值为10的开平方,直到五百多年后,印度和阿拉伯的数学家才得出这个数值.现有棱长为的正方体,利用张衡的结论可得该正方体的内切球的体积为______.
16. 已知,设函数,其定义域为或,则函数的最小值为______.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17. 已知函数的定义域为.
(Ⅰ)证明:函数是偶函数;
(Ⅱ)求函数的零点.
18. 在三棱锥中,、分别为、的中点,且,平面平面.
(1)证明:平面;
(2)证明:.
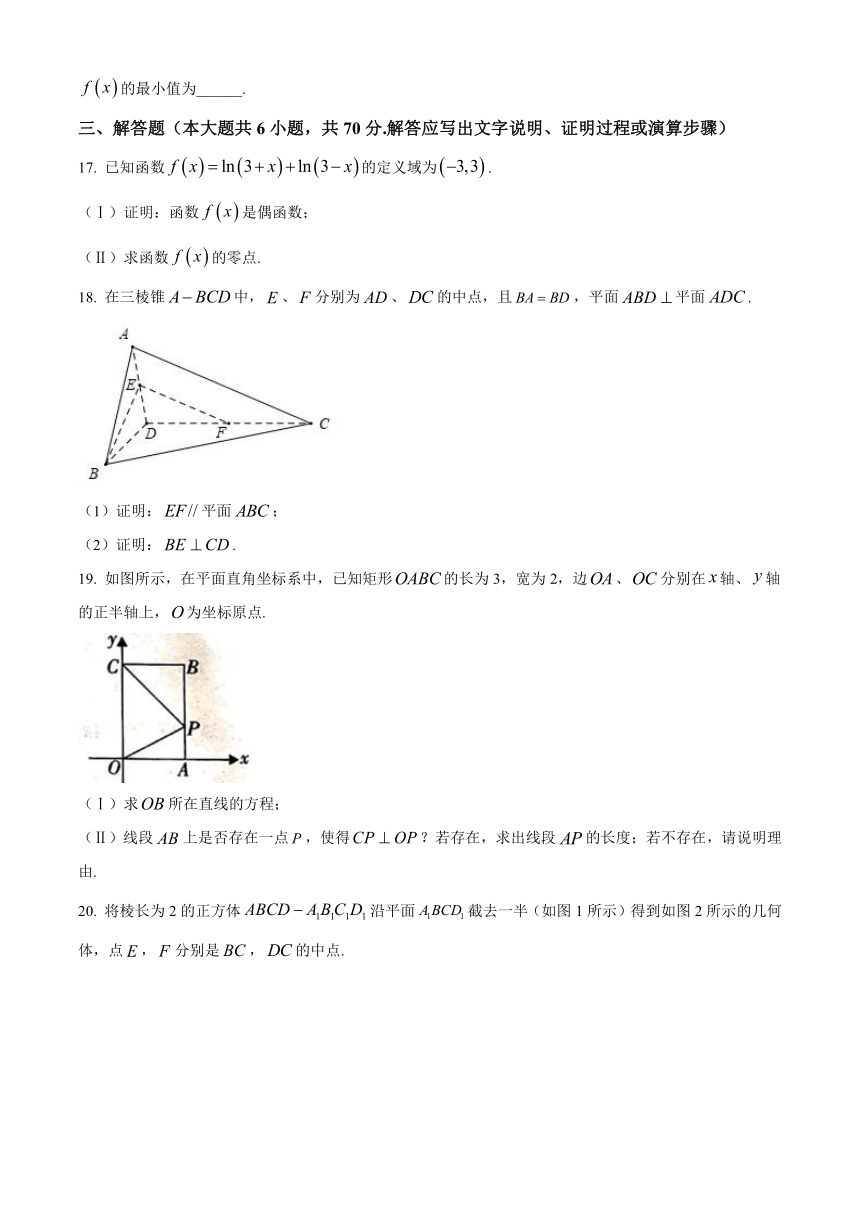
19. 如图所示,在平面直角坐标系中,已知矩形的长为3,宽为2,边、分别在轴、轴的正半轴上,为坐标原点.
(Ⅰ)求所在直线的方程;
(Ⅱ)线段上是否存在一点,使得?若存在,求出线段的长度;若不存在,请说明理由.
20. 将棱长为2的正方体沿平面截去一半(如图1所示)得到如图2所示的几何体,点,分别是,的中点.
图1 图2
(Ⅰ)证明:平面;
(Ⅱ)求三棱锥的体积.
21. 已知二次函数,.
(Ⅰ)若函数在上单调递减,求的取值范围;
(Ⅱ)若时,函数图像恰好在函数的图像上方(且恰好能取到等号),求实数的值.
22. 已知圆和轴相切于点,与轴正半轴交于、两点(在的左侧),且.
(Ⅰ)求圆的方程;
(Ⅱ)过点任作一条直线与圆:相交于点、,连接和,记和的斜率分别为,,求证:为定值.
咸阳市2020-2021学年度第一学期期末教学质量检测
高一数学试题(答案)
注意事项:
1.本试题共4页,满分150分,时间120分钟;
2.答卷前,考生须准确填写自己的姓名、准考证号,并认真核准条形码上的姓名、准号;
3.第Ⅰ卷选择题必须使用2B铅笔填涂,第Ⅱ卷非选择题必须使用0.5毫米黑色墨水签字笔书写,涂写要工整、清晰;
4.考试结束后,监考员将答题卡按顺序收回,装袋整理;试题卷不回收.
第Ⅰ卷(选择题共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 已知集合,,则( )
A. B. C. D.
【答案】C
2. 已知函数,则( )
A. B. C. D.
【答案】A
3. 圆与圆的位置关系为( )
A. 内切 B. 外切 C. 相交 D. 相离
【答案】B
4. 如图是一个几何体的三视图,它对应的几何体的名称是( )
A. 棱台 B. 圆台 C. 圆柱 D. 圆锥
【答案】B
5. 在直三棱柱的棱所在直线中,与直线异面的直线条数为( )
A. B. C. D.
【答案】C
6. 某学校高中部举行秋季田径运动会,甲、乙、丙、丁位同学代表高一(1)班参加男子组米接力跑比赛,甲同学负责跑第二棒.在比赛中,从甲接到接力棒到甲送出接力棒,甲同学的跑步速率(单位:)关于跑步时间(单位:)的函数图象最可能是( )
A. B.
C. . D.
【答案】C
7. 德国数学家狄利克雷在1837年提出:“如果对于的每一个值, 总有一个完全确定的值与之对应,则是的函数,”这个定义较清楚地说明了函数的内涵.只要有一个法则,使得取值范围中的每一个值,有一个确定的和它对应就行了,不管这个对应的法则是公式、图像、表格还是其它形式.已知函数由下表给出,则的值为( )
1 2 3 4 5
A. 2 B. 3 C. 4 D. 5
【答案】D
8. 已知平面平面,,,则下列结论一定正确是( )
A. ,是平行直线 B. ,是异面直线
C. ,是共面直线 D. ,是不相交直线
【答案】D
9. 已知,,,则,,的大小关系为( )
A. B. C. D.
【答案】C
10. 北京时间2020年12月17日1时59分,嫦娥五号返回器携带月球样品在预定区域安全着陆,嫦娥五号任务取得圆满成功.这是发挥新型举国体制优势攻坚克难取得又一重大成就,标志着中国航天向前迈出的一大步,将为深化人类对月球成因和太阳系演化历史的科学认知作出贡献.在所有航天工程中,火箭的作用毋庸置疑,在不考虑空气阻力的情况下,火箭的最大速度(km/s)和燃料的质量M(kg)、火箭(除燃料外)的质量m(kg)的函数关系是.按照这个规律,若火箭的最大速度可达到第二宇宙速度11.2km/s,则火箭的燃料质量M与火箭质量m之比约为( )
(参考数据:)
A. 0.0044 B. 2.0056 C. 1.0056 D. 0.0056
【答案】D
11. 设点,,若直线与线段有交点,则实数的取值范围是( )
A. B.
C. D.
【答案】C
12. 在数学课堂上,张老师给出一个定义在上的函数,甲、乙、丙、丁四位同学各说出了这个函数的一条性质:
甲:在上函数单调递减;
乙:在上函数单调递增;
丙:函数的图像关于直线对称;
丁:不是函数的最小值.
张老师说:你们四位同学中恰好有三个人说的正确,那么,你认为说法错误的同学是( )
A. 甲 B. 乙 C. 丙 D. 丁
【答案】B
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13. 函数的定义域为______.
【答案】
14. 已知,直线的倾斜角为,则直线的倾斜角为______.
【答案】
15. 张衡(78年~139年)是中国东汉时期杰出的天文学家、数学家、发明家、地理学家、文学家,他的数学著作有《算罔论》.张衡给立方体定名为质,给球体定名为浑.他研究过球的外切立方体体积和内接立方体体积,研究过球的体积,其中还定圆周率值为10的开平方,直到五百多年后,印度和阿拉伯的数学家才得出这个数值.现有棱长为的正方体,利用张衡的结论可得该正方体的内切球的体积为______.
【答案】3600
16. 已知,设函数,其定义域为或,则函数的最小值为______.
【答案】1
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17. 已知函数的定义域为.
(Ⅰ)证明:函数是偶函数;
(Ⅱ)求函数的零点.
【答案】(Ⅰ)证明见解析;(Ⅱ)和.
18. 在三棱锥中,、分别为、的中点,且,平面平面.
(1)证明:平面;
(2)证明:.
【答案】(1)证明见解析;(2)证明见解析.
19. 如图所示,在平面直角坐标系中,已知矩形的长为3,宽为2,边、分别在轴、轴的正半轴上,为坐标原点.
(Ⅰ)求所在直线的方程;
(Ⅱ)线段上是否存在一点,使得?若存在,求出线段的长度;若不存在,请说明理由.
【答案】(Ⅰ);(Ⅱ)不存在,理由见解析.
20. 将棱长为2的正方体沿平面截去一半(如图1所示)得到如图2所示的几何体,点,分别是,的中点.
图1 图2
(Ⅰ)证明:平面;
(Ⅱ)求三棱锥的体积.
【答案】(Ⅰ)证明见解析;(Ⅱ)1.
21. 已知二次函数,.
(Ⅰ)若函数在上单调递减,求的取值范围;
(Ⅱ)若时,函数图像恰好在函数的图像上方(且恰好能取到等号),求实数的值.
【答案】(Ⅰ);(Ⅱ).
22. 已知圆和轴相切于点,与轴正半轴交于、两点(在的左侧),且.
(Ⅰ)求圆的方程;
(Ⅱ)过点任作一条直线与圆:相交于点、,连接和,记和的斜率分别为,,求证:为定值.
【答案】(Ⅰ);(Ⅱ)证明见解析.
高一数学试题
注意事项:
1.本试题共4页,满分150分,时间120分钟;
2.答卷前,考生须准确填写自己的姓名、准考证号,并认真核准条形码上的姓名、准号;
3.第Ⅰ卷选择题必须使用2B铅笔填涂,第Ⅱ卷非选择题必须使用0.5毫米黑色墨水签字笔书写,涂写要工整、清晰;
4.考试结束后,监考员将答题卡按顺序收回,装袋整理;试题卷不回收.
第Ⅰ卷(选择题共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 已知集合,,则( )
A. B. C. D.
2. 已知函数,则( )
A. B. C. D.
3. 圆与圆的位置关系为( )
A. 内切 B. 外切 C. 相交 D. 相离
4. 如图是一个几何体的三视图,它对应的几何体的名称是( )
A. 棱台 B. 圆台 C. 圆柱 D. 圆锥
5. 在直三棱柱的棱所在直线中,与直线异面的直线条数为( )
A. B. C. D.
6. 某学校高中部举行秋季田径运动会,甲、乙、丙、丁位同学代表高一(1)班参加男子组米接力跑比赛,甲同学负责跑第二棒.在比赛中,从甲接到接力棒到甲送出接力棒,甲同学的跑步速率(单位:)关于跑步时间(单位:)的函数图象最可能是( )
A. B.
C. . D.
7. 德国数学家狄利克雷在1837年提出:“如果对于的每一个值, 总有一个完全确定的值与之对应,则是的函数,”这个定义较清楚地说明了函数的内涵.只要有一个法则,使得取值范围中的每一个值,有一个确定的和它对应就行了,不管这个对应的法则是公式、图像、表格还是其它形式.已知函数由下表给出,则的值为( )
1 2 3 4 5
A. 2 B. 3 C. 4 D. 5
8. 已知平面平面,,,则下列结论一定正确是( )
A. ,是平行直线 B. ,是异面直线
C. ,是共面直线 D. ,是不相交直线
9. 已知,,,则,,的大小关系为( )
A. B. C. D.
10. 北京时间2020年12月17日1时59分,嫦娥五号返回器携带月球样品在预定区域安全着陆,嫦娥五号任务取得圆满成功.这是发挥新型举国体制优势攻坚克难取得又一重大成就,标志着中国航天向前迈出的一大步,将为深化人类对月球成因和太阳系演化历史的科学认知作出贡献.在所有航天工程中,火箭的作用毋庸置疑,在不考虑空气阻力的情况下,火箭的最大速度(km/s)和燃料的质量M(kg)、火箭(除燃料外)的质量m(kg)的函数关系是.按照这个规律,若火箭的最大速度可达到第二宇宙速度11.2km/s,则火箭的燃料质量M与火箭质量m之比约为( )
(参考数据:)
A. 0.0044 B. 2.0056 C. 1.0056 D. 0.0056
11. 设点,,若直线与线段有交点,则实数的取值范围是( )
A. B.
C. D.
12. 在数学课堂上,张老师给出一个定义在上的函数,甲、乙、丙、丁四位同学各说出了这个函数的一条性质:
甲:在上函数单调递减;
乙:在上函数单调递增;
丙:函数的图像关于直线对称;
丁:不是函数的最小值.
张老师说:你们四位同学中恰好有三个人说的正确,那么,你认为说法错误的同学是( )
A. 甲 B. 乙 C. 丙 D. 丁
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13. 函数的定义域为______.
14. 已知,直线的倾斜角为,则直线的倾斜角为______.
15. 张衡(78年~139年)是中国东汉时期杰出的天文学家、数学家、发明家、地理学家、文学家,他的数学著作有《算罔论》.张衡给立方体定名为质,给球体定名为浑.他研究过球的外切立方体体积和内接立方体体积,研究过球的体积,其中还定圆周率值为10的开平方,直到五百多年后,印度和阿拉伯的数学家才得出这个数值.现有棱长为的正方体,利用张衡的结论可得该正方体的内切球的体积为______.
16. 已知,设函数,其定义域为或,则函数的最小值为______.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17. 已知函数的定义域为.
(Ⅰ)证明:函数是偶函数;
(Ⅱ)求函数的零点.
18. 在三棱锥中,、分别为、的中点,且,平面平面.
(1)证明:平面;
(2)证明:.
19. 如图所示,在平面直角坐标系中,已知矩形的长为3,宽为2,边、分别在轴、轴的正半轴上,为坐标原点.
(Ⅰ)求所在直线的方程;
(Ⅱ)线段上是否存在一点,使得?若存在,求出线段的长度;若不存在,请说明理由.
20. 将棱长为2的正方体沿平面截去一半(如图1所示)得到如图2所示的几何体,点,分别是,的中点.
图1 图2
(Ⅰ)证明:平面;
(Ⅱ)求三棱锥的体积.
21. 已知二次函数,.
(Ⅰ)若函数在上单调递减,求的取值范围;
(Ⅱ)若时,函数图像恰好在函数的图像上方(且恰好能取到等号),求实数的值.
22. 已知圆和轴相切于点,与轴正半轴交于、两点(在的左侧),且.
(Ⅰ)求圆的方程;
(Ⅱ)过点任作一条直线与圆:相交于点、,连接和,记和的斜率分别为,,求证:为定值.
咸阳市2020-2021学年度第一学期期末教学质量检测
高一数学试题(答案)
注意事项:
1.本试题共4页,满分150分,时间120分钟;
2.答卷前,考生须准确填写自己的姓名、准考证号,并认真核准条形码上的姓名、准号;
3.第Ⅰ卷选择题必须使用2B铅笔填涂,第Ⅱ卷非选择题必须使用0.5毫米黑色墨水签字笔书写,涂写要工整、清晰;
4.考试结束后,监考员将答题卡按顺序收回,装袋整理;试题卷不回收.
第Ⅰ卷(选择题共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 已知集合,,则( )
A. B. C. D.
【答案】C
2. 已知函数,则( )
A. B. C. D.
【答案】A
3. 圆与圆的位置关系为( )
A. 内切 B. 外切 C. 相交 D. 相离
【答案】B
4. 如图是一个几何体的三视图,它对应的几何体的名称是( )
A. 棱台 B. 圆台 C. 圆柱 D. 圆锥
【答案】B
5. 在直三棱柱的棱所在直线中,与直线异面的直线条数为( )
A. B. C. D.
【答案】C
6. 某学校高中部举行秋季田径运动会,甲、乙、丙、丁位同学代表高一(1)班参加男子组米接力跑比赛,甲同学负责跑第二棒.在比赛中,从甲接到接力棒到甲送出接力棒,甲同学的跑步速率(单位:)关于跑步时间(单位:)的函数图象最可能是( )
A. B.
C. . D.
【答案】C
7. 德国数学家狄利克雷在1837年提出:“如果对于的每一个值, 总有一个完全确定的值与之对应,则是的函数,”这个定义较清楚地说明了函数的内涵.只要有一个法则,使得取值范围中的每一个值,有一个确定的和它对应就行了,不管这个对应的法则是公式、图像、表格还是其它形式.已知函数由下表给出,则的值为( )
1 2 3 4 5
A. 2 B. 3 C. 4 D. 5
【答案】D
8. 已知平面平面,,,则下列结论一定正确是( )
A. ,是平行直线 B. ,是异面直线
C. ,是共面直线 D. ,是不相交直线
【答案】D
9. 已知,,,则,,的大小关系为( )
A. B. C. D.
【答案】C
10. 北京时间2020年12月17日1时59分,嫦娥五号返回器携带月球样品在预定区域安全着陆,嫦娥五号任务取得圆满成功.这是发挥新型举国体制优势攻坚克难取得又一重大成就,标志着中国航天向前迈出的一大步,将为深化人类对月球成因和太阳系演化历史的科学认知作出贡献.在所有航天工程中,火箭的作用毋庸置疑,在不考虑空气阻力的情况下,火箭的最大速度(km/s)和燃料的质量M(kg)、火箭(除燃料外)的质量m(kg)的函数关系是.按照这个规律,若火箭的最大速度可达到第二宇宙速度11.2km/s,则火箭的燃料质量M与火箭质量m之比约为( )
(参考数据:)
A. 0.0044 B. 2.0056 C. 1.0056 D. 0.0056
【答案】D
11. 设点,,若直线与线段有交点,则实数的取值范围是( )
A. B.
C. D.
【答案】C
12. 在数学课堂上,张老师给出一个定义在上的函数,甲、乙、丙、丁四位同学各说出了这个函数的一条性质:
甲:在上函数单调递减;
乙:在上函数单调递增;
丙:函数的图像关于直线对称;
丁:不是函数的最小值.
张老师说:你们四位同学中恰好有三个人说的正确,那么,你认为说法错误的同学是( )
A. 甲 B. 乙 C. 丙 D. 丁
【答案】B
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13. 函数的定义域为______.
【答案】
14. 已知,直线的倾斜角为,则直线的倾斜角为______.
【答案】
15. 张衡(78年~139年)是中国东汉时期杰出的天文学家、数学家、发明家、地理学家、文学家,他的数学著作有《算罔论》.张衡给立方体定名为质,给球体定名为浑.他研究过球的外切立方体体积和内接立方体体积,研究过球的体积,其中还定圆周率值为10的开平方,直到五百多年后,印度和阿拉伯的数学家才得出这个数值.现有棱长为的正方体,利用张衡的结论可得该正方体的内切球的体积为______.
【答案】3600
16. 已知,设函数,其定义域为或,则函数的最小值为______.
【答案】1
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17. 已知函数的定义域为.
(Ⅰ)证明:函数是偶函数;
(Ⅱ)求函数的零点.
【答案】(Ⅰ)证明见解析;(Ⅱ)和.
18. 在三棱锥中,、分别为、的中点,且,平面平面.
(1)证明:平面;
(2)证明:.
【答案】(1)证明见解析;(2)证明见解析.
19. 如图所示,在平面直角坐标系中,已知矩形的长为3,宽为2,边、分别在轴、轴的正半轴上,为坐标原点.
(Ⅰ)求所在直线的方程;
(Ⅱ)线段上是否存在一点,使得?若存在,求出线段的长度;若不存在,请说明理由.
【答案】(Ⅰ);(Ⅱ)不存在,理由见解析.
20. 将棱长为2的正方体沿平面截去一半(如图1所示)得到如图2所示的几何体,点,分别是,的中点.
图1 图2
(Ⅰ)证明:平面;
(Ⅱ)求三棱锥的体积.
【答案】(Ⅰ)证明见解析;(Ⅱ)1.
21. 已知二次函数,.
(Ⅰ)若函数在上单调递减,求的取值范围;
(Ⅱ)若时,函数图像恰好在函数的图像上方(且恰好能取到等号),求实数的值.
【答案】(Ⅰ);(Ⅱ).
22. 已知圆和轴相切于点,与轴正半轴交于、两点(在的左侧),且.
(Ⅰ)求圆的方程;
(Ⅱ)过点任作一条直线与圆:相交于点、,连接和,记和的斜率分别为,,求证:为定值.
【答案】(Ⅰ);(Ⅱ)证明见解析.
同课章节目录
