2020—2021学年人教版数学七年级下册5.1.1 相交线 课件(20张)
文档属性
| 名称 | 2020—2021学年人教版数学七年级下册5.1.1 相交线 课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 00:00:00 | ||
图片预览





文档简介
第五章 相交线与平行线
第1课时 相交线
5.1 相交线
学习目标
1.通过动手、操作、推断、交流等活动,进一步发展空间观念,培养识图能力,推理能力和有条理表达能力;
2.在具体情境中了解邻补角、对顶角,能找出图形中的一个角的邻补角和对顶角,理解对顶角相等,并能运用它解决一些简单问题.
课堂导入
这节课我们先来学习相交线.
课堂导入
观察、发现 这里有一把剪刀,握紧剪刀的把手,就能剪开物体,你能说出其中的道理吗?如果把剪子的构造 抽象成一个几何图形,会是什么样的图形?请你在纸上画出来.
剪刀的构造可看作两条相交的直线,剪刀刃之间的角就是相交直线所成的角.
我们可以利用角的数量关系来研究两条直线相交的位置关系.
新知讲解
1. 相交线的概念
相交线的概念:如果两条直线只有一个公共点,那么我们就说这两条直线相交,它们的公共点叫做交点.
新知讲解
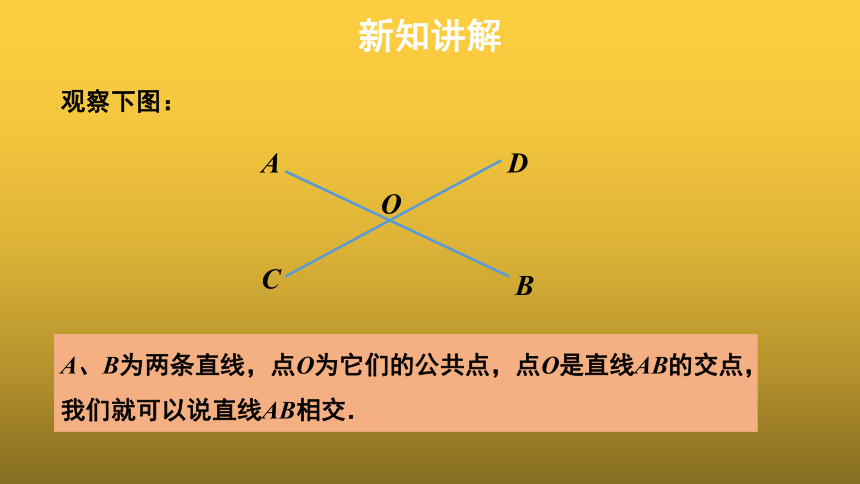
观察下图:
A
B
C
D
O
A、B为两条直线,点O为它们的公共点,点O是直线AB的交点,我们就可以说直线AB相交.
新知讲解
2. 两条直线相交线所成的角
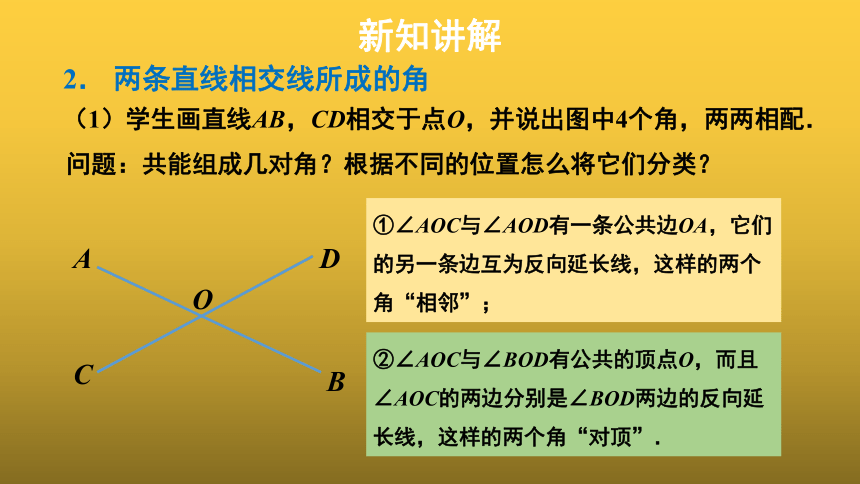
(1)学生画直线AB,CD相交于点O,并说出图中4个角,两两相配.
问题:共能组成几对角?根据不同的位置怎么将它们分类?
A
B
C
D
O
①∠AOC与∠AOD有一条公共边OA,它们的另一条边互为反向延长线,这样的两个角“相邻”;
②∠AOC与∠BOD有公共的顶点O,而且∠AOC的两边分别是∠BOD两边的反向延长线,这样的两个角“对顶”.
新知讲解
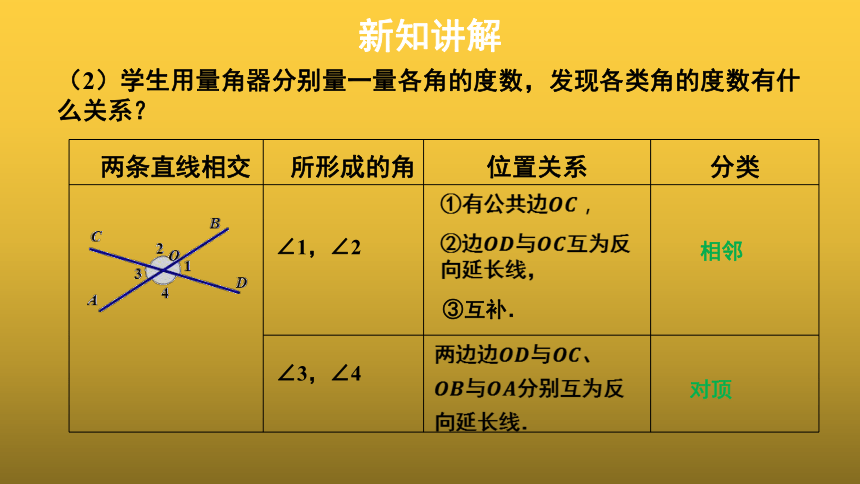
(2)学生用量角器分别量一量各角的度数,发现各类角的度数有什么关系?
{5940675A-B579-460E-94D1-54222C63F5DA}两条直线相交
所形成的角
位置关系
分类
?
?
?
∠1,∠2
③互补.
①有公共边????????,
?
②边????????与????????互为反向延长线,
?
两边边????????与????????、????????与????????分别互为反向延长线.
?
相邻
对顶
∠3,∠4
新知讲解
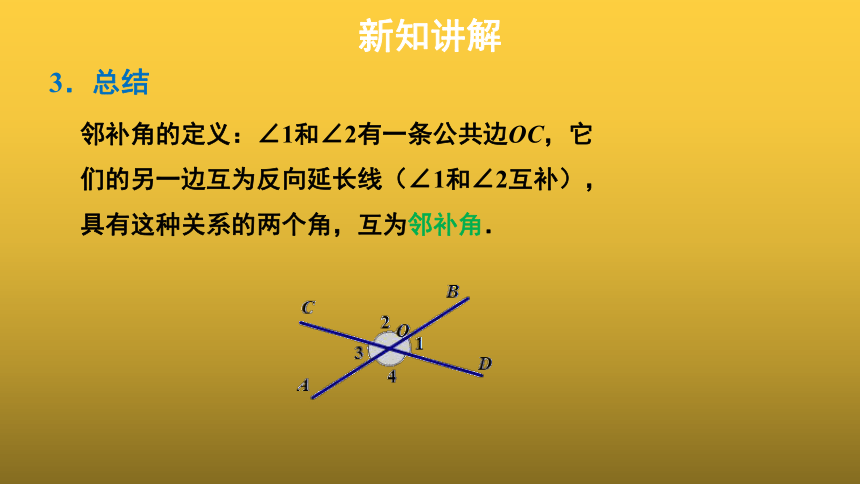
邻补角的定义:∠1和∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角,互为邻补角.
3.总结
对顶角的定义:∠1和∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
新知讲解
对顶角的性质:
∠????+∠????=????????????°
?
∠????+∠????=????????????°
?
∠????=∠????
?
∠????+∠????=????????????°
?
∠????+∠????=????????????°
?
∠????=∠????
?
对顶角相等.
新知讲解
4.知识拓展
相交线在我们生活中有哪些应用呢,下面我们来一起看下.
通过介绍九树成行,体现数学来源于生活,提高学生的学习兴趣.
典型例题
【例题1】如图,直线????????,????????,????????相交于点????,则图中一共有_______对对顶角,________对邻补角.
?
分析:
两条直线相交形成两对对顶角,四对邻补角.
直线????????,????????,????????相交于点????
?
????????,????????相交
?
????????,????????相交
?
????????,????????相交
?
2对顶,4邻补
2对顶,4邻补
2对顶,4邻补
6
12
【例题2】如图,将一张长方形的纸片按图中的方式折叠,????????′和????????′重合,????????,????????为折痕,∠????????????的度数为________.
?
分析:
折叠
∠????+∠????+∠????+∠????=????????????°
?
∠????=∠????, ∠????=∠3
?
∠????+∠????=∠????+∠3
?
∠????+∠????=????????°
?
90°
典型例题
【例题3】如图,已知直线????????,????????相交于????点,????????平分∠????????????, ∠????????????=????????????°,则 ∠????????????的度数为__________.
?
分析:
∠????????????=????????°
?
∠????????????=????????°
?
∠????????????=????????????°
?
∠????????????+∠????????????=????????????°(邻补角)
?
∠????????????=????????∠????????????
?
????????°
?
典型例题
1.如图,已知:直线AB与CD相交于点O,∠1=50度.则∠2=______度,∠3=________度.
????????
?
????????????
?
2.如图,直线AB、CD相交于点O,已知:∠AOC=70°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,则∠AOE=_______.
152°
随堂练习
3.如图,已知AB、CD相交于点O,OE⊥AB,∠EOC=28°,则∠AOD=_________.
62°
随堂练习
4.如图,直线AB与直线CD相交于点O,OE⊥AB,OF平分∠AOD,∠COE=28°.求∠AOC和∠DOF的度数.
∵OE⊥AB,
∴∠BOE=90°,
∴∠BOC=∠BOE+∠COE=90°+28°=118°,
∴∠AOC=180°-∠BOC=180°-118°=62°;
∠AOD=∠BOC=118°,
又OF平分∠AOD,
∴∠DOF=????????∠AOD= ????????×118°=59°.
?
解:
随堂练习
①邻补角:有一条公共边,另一条边互为反向延长线的两个角互为邻补角.
②对顶角:有公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,这样的两个角叫做对顶角.
对顶角相等
两条直线相交,所成的四个角中:
课堂小结
再见
第1课时 相交线
5.1 相交线
学习目标
1.通过动手、操作、推断、交流等活动,进一步发展空间观念,培养识图能力,推理能力和有条理表达能力;
2.在具体情境中了解邻补角、对顶角,能找出图形中的一个角的邻补角和对顶角,理解对顶角相等,并能运用它解决一些简单问题.
课堂导入
这节课我们先来学习相交线.
课堂导入
观察、发现 这里有一把剪刀,握紧剪刀的把手,就能剪开物体,你能说出其中的道理吗?如果把剪子的构造 抽象成一个几何图形,会是什么样的图形?请你在纸上画出来.
剪刀的构造可看作两条相交的直线,剪刀刃之间的角就是相交直线所成的角.
我们可以利用角的数量关系来研究两条直线相交的位置关系.
新知讲解
1. 相交线的概念
相交线的概念:如果两条直线只有一个公共点,那么我们就说这两条直线相交,它们的公共点叫做交点.
新知讲解
观察下图:
A
B
C
D
O
A、B为两条直线,点O为它们的公共点,点O是直线AB的交点,我们就可以说直线AB相交.
新知讲解
2. 两条直线相交线所成的角
(1)学生画直线AB,CD相交于点O,并说出图中4个角,两两相配.
问题:共能组成几对角?根据不同的位置怎么将它们分类?
A
B
C
D
O
①∠AOC与∠AOD有一条公共边OA,它们的另一条边互为反向延长线,这样的两个角“相邻”;
②∠AOC与∠BOD有公共的顶点O,而且∠AOC的两边分别是∠BOD两边的反向延长线,这样的两个角“对顶”.
新知讲解
(2)学生用量角器分别量一量各角的度数,发现各类角的度数有什么关系?
{5940675A-B579-460E-94D1-54222C63F5DA}两条直线相交
所形成的角
位置关系
分类
?
?
?
∠1,∠2
③互补.
①有公共边????????,
?
②边????????与????????互为反向延长线,
?
两边边????????与????????、????????与????????分别互为反向延长线.
?
相邻
对顶
∠3,∠4
新知讲解
邻补角的定义:∠1和∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角,互为邻补角.
3.总结
对顶角的定义:∠1和∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
新知讲解
对顶角的性质:
∠????+∠????=????????????°
?
∠????+∠????=????????????°
?
∠????=∠????
?
∠????+∠????=????????????°
?
∠????+∠????=????????????°
?
∠????=∠????
?
对顶角相等.
新知讲解
4.知识拓展
相交线在我们生活中有哪些应用呢,下面我们来一起看下.
通过介绍九树成行,体现数学来源于生活,提高学生的学习兴趣.
典型例题
【例题1】如图,直线????????,????????,????????相交于点????,则图中一共有_______对对顶角,________对邻补角.
?
分析:
两条直线相交形成两对对顶角,四对邻补角.
直线????????,????????,????????相交于点????
?
????????,????????相交
?
????????,????????相交
?
????????,????????相交
?
2对顶,4邻补
2对顶,4邻补
2对顶,4邻补
6
12
【例题2】如图,将一张长方形的纸片按图中的方式折叠,????????′和????????′重合,????????,????????为折痕,∠????????????的度数为________.
?
分析:
折叠
∠????+∠????+∠????+∠????=????????????°
?
∠????=∠????, ∠????=∠3
?
∠????+∠????=∠????+∠3
?
∠????+∠????=????????°
?
90°
典型例题
【例题3】如图,已知直线????????,????????相交于????点,????????平分∠????????????, ∠????????????=????????????°,则 ∠????????????的度数为__________.
?
分析:
∠????????????=????????°
?
∠????????????=????????°
?
∠????????????=????????????°
?
∠????????????+∠????????????=????????????°(邻补角)
?
∠????????????=????????∠????????????
?
????????°
?
典型例题
1.如图,已知:直线AB与CD相交于点O,∠1=50度.则∠2=______度,∠3=________度.
????????
?
????????????
?
2.如图,直线AB、CD相交于点O,已知:∠AOC=70°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,则∠AOE=_______.
152°
随堂练习
3.如图,已知AB、CD相交于点O,OE⊥AB,∠EOC=28°,则∠AOD=_________.
62°
随堂练习
4.如图,直线AB与直线CD相交于点O,OE⊥AB,OF平分∠AOD,∠COE=28°.求∠AOC和∠DOF的度数.
∵OE⊥AB,
∴∠BOE=90°,
∴∠BOC=∠BOE+∠COE=90°+28°=118°,
∴∠AOC=180°-∠BOC=180°-118°=62°;
∠AOD=∠BOC=118°,
又OF平分∠AOD,
∴∠DOF=????????∠AOD= ????????×118°=59°.
?
解:
随堂练习
①邻补角:有一条公共边,另一条边互为反向延长线的两个角互为邻补角.
②对顶角:有公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,这样的两个角叫做对顶角.
对顶角相等
两条直线相交,所成的四个角中:
课堂小结
再见
