初中数学冀教版八年级下册18.4频数分布表与直方图练习题普通用卷(word解析版)
文档属性
| 名称 | 初中数学冀教版八年级下册18.4频数分布表与直方图练习题普通用卷(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 246.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 00:00:00 | ||
图片预览


文档简介
初中数学晋教版八年级下册第十八章18.4频数分布表与直方图练习题
一、选择题
某学校对600名女生的身高进行了测量,身高在单位:这一小组的频率为,则该组的人数为
A.
100
B.
150
C.
200
D.
250
小丽抛一枚硬币10次,其中有6次正面朝上,则反面朝上的频数是?
?
A.
6
B.
C.
4
D.
一组数据共50个,分为6组,第组的频数分别为5,7,8,10,第5组的频率为,则第6组的频数为
A.
10
B.
11
C.
12
D.
15
一组数据共100个,分为6组,第组的频数分别为10,14,16,20,第5组的频率为,则第6组的频数为
A.
20
B.
22
C.
24
D.
30
在一次调查中,出现A种情况的频率为,其余情况出现的频数之和为70,则这次调查的总数为
A.
140
B.
100
C.
90
D.
70
“早发现,早报告,早隔离,早治疗”是我国抗击“新冠肺炎”的宝贵经验,其中“早”字出现的频率是
A.
B.
C.
D.
在对n个数据进行整理的频数分布表中,各组的频数之和等于
A.
n
B.
1
C.
2
n
D.
3
n
为绘制一组数据的频数分布直方图,首先要算出这组数据的变动范围,即是指数据的
A.
最大值
B.
最小值
C.
个数
D.
最大值与最小值的差
体育委员统计了七班全体同学60秒跳绳的次数,并列出下面的频数分布表:
次数
频数
2
4
21
14
7
3
1
给出以下结论:全班有52名学生;组距是20;组数是7;跳绳次数在范围的学生约占全班学生的其中正确结论的个数是?
???
A.
1
B.
2
C.
3
D.
4
郑州市实施垃圾分类以来,为了调动居民参与垃圾分类的积极性,学府小区开展了垃圾分类积分兑换奖品活动.随机抽取了若干户12月份的积分情况,并对抽取的样本进行了整理得到下列不完整的统计表:
积分分
频数
频率
6
12
24
a
18
根据以上信息可得
A.
B.
C.
D.
二、填空题
在一个样本中,100个数据分布在5个组内,第一、二、四、五组的频数分别为9,16,40,15,若用扇形图对这些数据进行统计,则第三组对应的扇形圆心角的度数为______.
在一个样本容量为80的样本所绘制的频数分布直方图中,第一、二、三、四小组所对应的各个长方形高的比为,那么第四组的频数是__________.
一组数据4,,,4,,4,,4中,出现次数最多的数是4,其频率是______
.
为了了解某中学八年级男生的身体发育情况,从该中学八年级男生中随机抽取40名男生的身高进行了测量,已知身高单位:在这一小组的频数为6,则身高在这一小组的频率是______
.
三、解答题
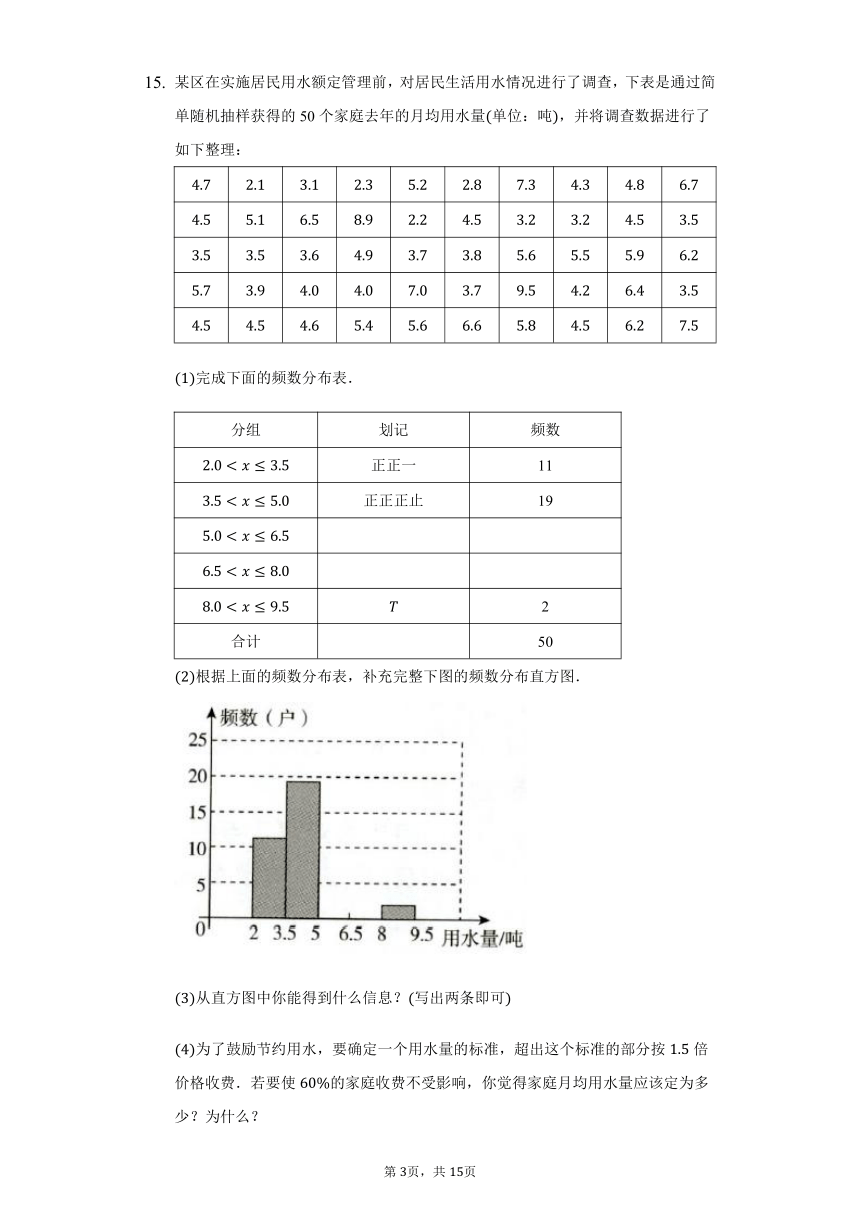
某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年的月均用水量单位:吨,并将调查数据进行了如下整理:
完成下面的频数分布表.
分组
划记
频数
正正一
11
正正正止
19
2
合计
50
根据上面的频数分布表,补充完整下图的频数分布直方图.
从直方图中你能得到什么信息?写出两条即可
为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按倍价格收费.若要使的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
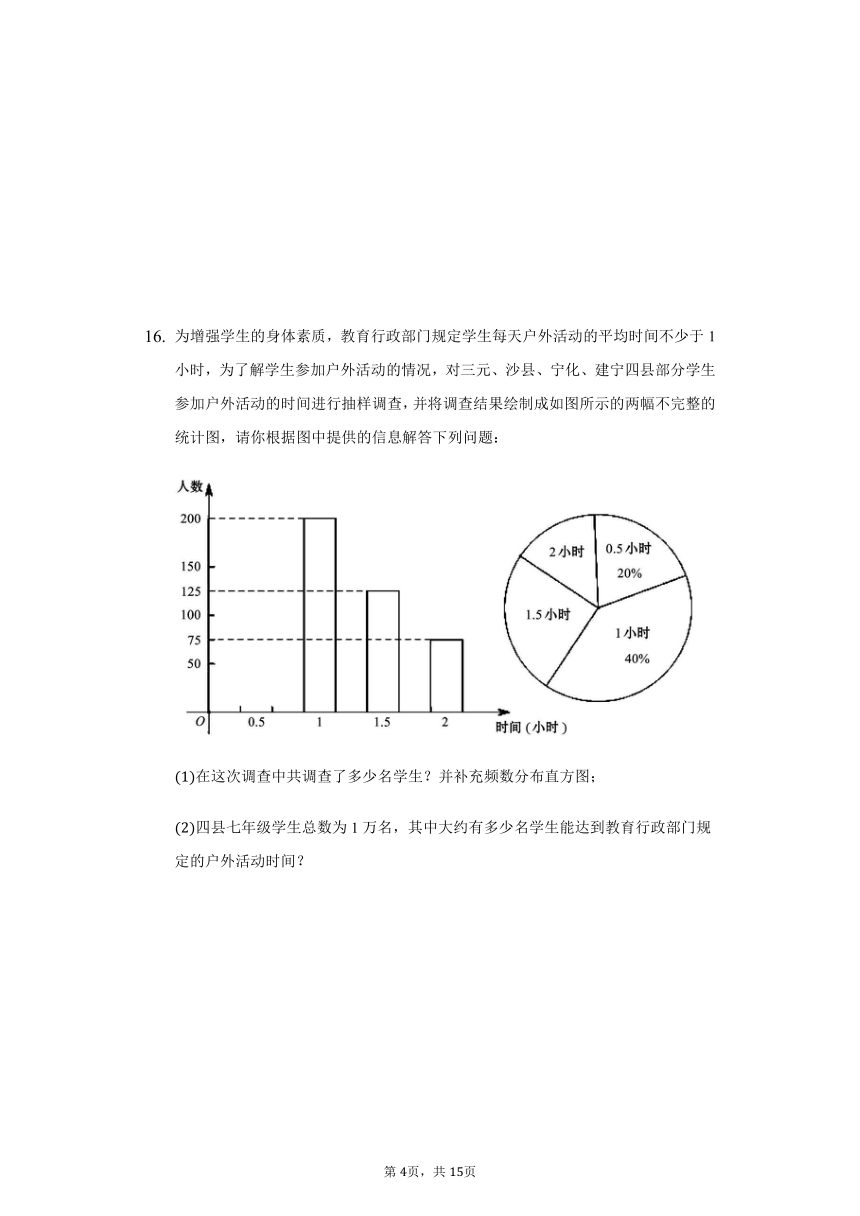
为增强学生的身体素质,教育行政部门规定学生每天户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对三元、沙县、宁化、建宁四县部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
在这次调查中共调查了多少名学生?并补充频数分布直方图;
四县七年级学生总数为1万名,其中大约有多少名学生能达到教育行政部门规定的户外活动时间?
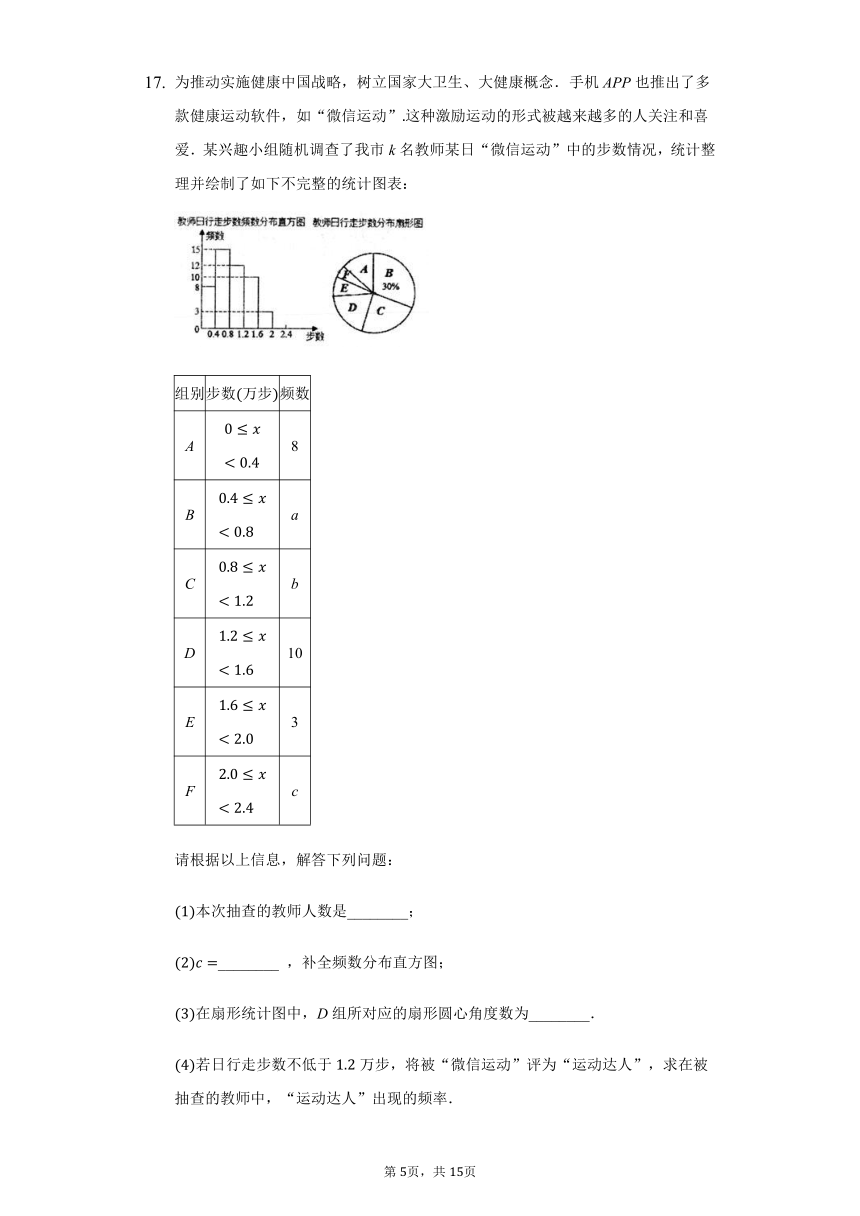
为推动实施健康中国战略,树立国家大卫生、大健康概念.手机APP也推出了多款健康运动软件,如“微信运动”这种激励运动的形式被越来越多的人关注和喜爱.某兴趣小组随机调查了我市k名教师某日“微信运动”中的步数情况,统计整理并绘制了如下不完整的统计图表:
组别
步数万步
频数
A
8
B
a
C
b
D
10
E
3
F
c
请根据以上信息,解答下列问题:
本次抽查的教师人数是________;
________
,补全频数分布直方图;
在扇形统计图中,D组所对应的扇形圆心角度数为________.
若日行走步数不低于万步,将被“微信运动”评为“运动达人”,求在被抽查的教师中,“运动达人”出现的频率.
为了解2020年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作了不完整的频数分布表.
分数分
频数
百分比
30
90
b
a
60
c
请根据图表提供的信息,解答下列问题:
在表中:__________;__________,__________;
请补全频数分布直方图;
若将抽取的成绩绘制成扇形统计图,请计算成绩在“”所在扇形的圆心角的度数.
答案和解析
1.【答案】B
【解析】
【分析】
此题考查频率、频数的关系:频率频数数据总数.能够灵活运用此公式是解题的关键.根据频率频数数据总数,得频数数据总数频率,将数据代入即可求解.
【解答】
解:根据题意,得
该组的人数为人.
故选B.
2.【答案】C
【解析】
【分析】
本题考查频数概念,频数是对落在各个小组内的数据进行累计,得到各小组内的数据的个数.
本题根据频数概念即可得.
【解答】
解:依题意得,
次,
反面朝上4次,即出现反面朝上的频数是4.
故选:C
3.【答案】A
【解析】
【分析】
本题是对频率、频数灵活运用的综合考查.用到的知识点:
各小组频数之和等于数据总和,各小组频率之和等于1;频率、频数的关系:频率频数数据总数.
先根据频数总数频率,求得第五组频数;再根据各组的频数和等于总数,求得第六组的频数.
【解答】
解:根据题意,得
第五组频数是,
故第六组的频数是.
故选A.
4.【答案】A
【解析】解:一组数据共100个,第5组的频率为,
第5组的频数是:,
一组数据共100个,分为6组,第组的频数分别为10,14,16,20,
第6组的频数为:.
故选:A.
直接利用频数与频率的关系得出第5组的频数,进而得出答案.
此题主要考查了频数与频率,正确得出第5组频数是解题关键.
5.【答案】B
【解析】
【分析】
本题考查了频数和频率,解答本题的关键是掌握频率先求出其余情况出现的频率,然后根据频率求解.
【解答】
解:其余情况出现的频率,
则这次调查的总数.
故选B.
6.【答案】D
【解析】解:“早”字出现的频率是:,
故选:D.
利用频率的计算方法计算即可.
此题主要考查了频率,关键是掌握频率频数总数.
7.【答案】A
【解析】
【分析】
本题考查的是对频数的灵活运用,了解基本概念是解决本题的关键根据各小组频数之和等于数据总和;可得答案.
【解答】
解:根据频数的概念,各小组频数之和等于数据总和,即n;
故选A.
8.【答案】D
【解析】
【分析】
本题主要考查频率直方图的定义及学生对其的准备理解.频率直方图是按照数据从小到大的顺序排列,包括所有的数据,即数据的变化范围是指数据的最大值和最小值的差.
【解答】
解:数据的变动范围是指数据的最大值与最小值的差.
故选D.
9.【答案】D
【解析】解:全班学生数为人,此结论正确;
由频数分布表可知,组距为,组数为7组,故均正确;
跳绳次数在范围的学生占全班学生的,故此结论正确;
故选:D.
将各组频数相加即可得;由频率分布表即可知组数和组距;将范围的两组频数相加,再将其除以总人数即可得百分比.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力.读图时要全面细致,同时,解题方法要灵活多样,切忌死记硬背.
10.【答案】C
【解析】
【分析】
此题考查了频数率分布表,熟练掌握频数、频率与总数之间的关系是解题的关键.根据的频数和频率求出抽取的总数,再根据频率频数总数求出a即可.
【解答】
解:抽取的样本总数为,
.
故选C.
11.【答案】
【解析】解:个数据分布在5个组内,第一、二、四、五组的频数分别为9,16,40,15,
第三组数据的频数为20,
第三组对应的扇形圆心角的度数为,
故答案为:.
先根据题意,得到第三组数据的频数,再根据扇形圆心角计算公式进行计算即可.
本题主要考查了扇形统计图的应用,解题时注意:用整个圆的面积表示总数单位,用圆的扇形面积表示各部分占总数的百分数.
12.【答案】8
【解析】
【分析】
此题考查了频数率分布直方图,要知道,频数分布直方图中各个长方形的高之比即为各组频数之比.频数分布直方图中,各个长方形的高之比依次为2:3:4:1,则指各组频数之比为2:3:4:1,据此即可求出第四小组的频数.
【解答】
解:第四小组的频数:.
故答案为8.
13.【答案】
【解析】解:4出现的频率是.
故答案为:.
用4出现的次数除以数据的个数即可.
本题考查了频数与频率:频数是指每个对象出现的次数.频率是指每个对象出现的次数与总次数的比值或者百分比,即频率频数总数.
14.【答案】
【解析】解:根据题意,得:
频率.
故答案为.
根据频率公式作答即可.
本题是对频率、频数灵活运用的综合考查.熟练运用公式频率作答即可.
15.【答案】解:频数分布表如下:
分组
划记
频数
?
正正一
11
?
正正正止
19
?
13
正
5
2
合计
50
频数分布直方图如下:
从直方图可以看出:居民月平均用水量大部分在至之间;居民月平均用水量在范围内的最多,有19户;
要使的家庭收费不受影响,你觉得家庭月均用水量应该定为5吨,因为月平均用水量不超过5吨的有30户,.
【解析】本题考查读频数分布直方图和频数分布表的能力及利用统计图表获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
根据题中给出的50个数据,从中分别找出与??的个数,进行划记,得到对应的频数,进而完成频数分布表和频数分布直方图;
本题答案不唯一.例如:从直方图可以看出:居民月平均用水量大部分在至之间;居民月平均用水量在范围内的最多,有19户;
由于,所以为了鼓励节约用水,要使的家庭收费不受影响,即要使30户的家庭收费不受影响,而,故家庭月均用水量应该定为5吨.
16.【答案】解:名,?
名,
频数分布直方图如图:
答:在这次调查中共调查了500名学生;
名;
答:大约有8000名学生能达到教育行政部门规定的户外活动时间.
【解析】本题主要考查了条形统计图,扇形统计图及用样本估计总体,解题的关键是读懂统计图,能正确的从统计图中获取信息.
由1小时的人数及其百分比可得总人数,求得小时的人数,作图即可;
用总人数乘以样本的百分比可得答案.
17.【答案】解:;
;
画图如下:
;
根据题意,50人中日行走步数不低于万步的总人数为人,
所占比例为,
答:在被抽查的教师中,“运动达人”出现的频率为.
【解析】此题考查了频数分布直方图,扇形统计图,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
由B组人数及其所占百分比可得被调查的总人数;
从图中获取a,b的值,然后便可得出c,再补全频数分布直方图即可;
用乘以D组人数占被调查人数的比例即可得出结果;
先得出50人中日行走步数不低于万步的总人数为人,便可得出结果.
【解答】
解:本次抽查的教师人数是:人,
故答案为50人;
从图中可知,,,
,
频数分布直方图见答案,
故答案为2;
组所对应的扇形圆心角度数为,
故答案案为;
见答案.
18.【答案】解:,,.
补全频数分布直方图如图所示.
成绩在“”所在扇形的圆心角的度数为:.
【解析】略
第2页,共2页
第1页,共1页
一、选择题
某学校对600名女生的身高进行了测量,身高在单位:这一小组的频率为,则该组的人数为
A.
100
B.
150
C.
200
D.
250
小丽抛一枚硬币10次,其中有6次正面朝上,则反面朝上的频数是?
?
A.
6
B.
C.
4
D.
一组数据共50个,分为6组,第组的频数分别为5,7,8,10,第5组的频率为,则第6组的频数为
A.
10
B.
11
C.
12
D.
15
一组数据共100个,分为6组,第组的频数分别为10,14,16,20,第5组的频率为,则第6组的频数为
A.
20
B.
22
C.
24
D.
30
在一次调查中,出现A种情况的频率为,其余情况出现的频数之和为70,则这次调查的总数为
A.
140
B.
100
C.
90
D.
70
“早发现,早报告,早隔离,早治疗”是我国抗击“新冠肺炎”的宝贵经验,其中“早”字出现的频率是
A.
B.
C.
D.
在对n个数据进行整理的频数分布表中,各组的频数之和等于
A.
n
B.
1
C.
2
n
D.
3
n
为绘制一组数据的频数分布直方图,首先要算出这组数据的变动范围,即是指数据的
A.
最大值
B.
最小值
C.
个数
D.
最大值与最小值的差
体育委员统计了七班全体同学60秒跳绳的次数,并列出下面的频数分布表:
次数
频数
2
4
21
14
7
3
1
给出以下结论:全班有52名学生;组距是20;组数是7;跳绳次数在范围的学生约占全班学生的其中正确结论的个数是?
???
A.
1
B.
2
C.
3
D.
4
郑州市实施垃圾分类以来,为了调动居民参与垃圾分类的积极性,学府小区开展了垃圾分类积分兑换奖品活动.随机抽取了若干户12月份的积分情况,并对抽取的样本进行了整理得到下列不完整的统计表:
积分分
频数
频率
6
12
24
a
18
根据以上信息可得
A.
B.
C.
D.
二、填空题
在一个样本中,100个数据分布在5个组内,第一、二、四、五组的频数分别为9,16,40,15,若用扇形图对这些数据进行统计,则第三组对应的扇形圆心角的度数为______.
在一个样本容量为80的样本所绘制的频数分布直方图中,第一、二、三、四小组所对应的各个长方形高的比为,那么第四组的频数是__________.
一组数据4,,,4,,4,,4中,出现次数最多的数是4,其频率是______
.
为了了解某中学八年级男生的身体发育情况,从该中学八年级男生中随机抽取40名男生的身高进行了测量,已知身高单位:在这一小组的频数为6,则身高在这一小组的频率是______
.
三、解答题
某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年的月均用水量单位:吨,并将调查数据进行了如下整理:
完成下面的频数分布表.
分组
划记
频数
正正一
11
正正正止
19
2
合计
50
根据上面的频数分布表,补充完整下图的频数分布直方图.
从直方图中你能得到什么信息?写出两条即可
为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按倍价格收费.若要使的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
为增强学生的身体素质,教育行政部门规定学生每天户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对三元、沙县、宁化、建宁四县部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
在这次调查中共调查了多少名学生?并补充频数分布直方图;
四县七年级学生总数为1万名,其中大约有多少名学生能达到教育行政部门规定的户外活动时间?
为推动实施健康中国战略,树立国家大卫生、大健康概念.手机APP也推出了多款健康运动软件,如“微信运动”这种激励运动的形式被越来越多的人关注和喜爱.某兴趣小组随机调查了我市k名教师某日“微信运动”中的步数情况,统计整理并绘制了如下不完整的统计图表:
组别
步数万步
频数
A
8
B
a
C
b
D
10
E
3
F
c
请根据以上信息,解答下列问题:
本次抽查的教师人数是________;
________
,补全频数分布直方图;
在扇形统计图中,D组所对应的扇形圆心角度数为________.
若日行走步数不低于万步,将被“微信运动”评为“运动达人”,求在被抽查的教师中,“运动达人”出现的频率.
为了解2020年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作了不完整的频数分布表.
分数分
频数
百分比
30
90
b
a
60
c
请根据图表提供的信息,解答下列问题:
在表中:__________;__________,__________;
请补全频数分布直方图;
若将抽取的成绩绘制成扇形统计图,请计算成绩在“”所在扇形的圆心角的度数.
答案和解析
1.【答案】B
【解析】
【分析】
此题考查频率、频数的关系:频率频数数据总数.能够灵活运用此公式是解题的关键.根据频率频数数据总数,得频数数据总数频率,将数据代入即可求解.
【解答】
解:根据题意,得
该组的人数为人.
故选B.
2.【答案】C
【解析】
【分析】
本题考查频数概念,频数是对落在各个小组内的数据进行累计,得到各小组内的数据的个数.
本题根据频数概念即可得.
【解答】
解:依题意得,
次,
反面朝上4次,即出现反面朝上的频数是4.
故选:C
3.【答案】A
【解析】
【分析】
本题是对频率、频数灵活运用的综合考查.用到的知识点:
各小组频数之和等于数据总和,各小组频率之和等于1;频率、频数的关系:频率频数数据总数.
先根据频数总数频率,求得第五组频数;再根据各组的频数和等于总数,求得第六组的频数.
【解答】
解:根据题意,得
第五组频数是,
故第六组的频数是.
故选A.
4.【答案】A
【解析】解:一组数据共100个,第5组的频率为,
第5组的频数是:,
一组数据共100个,分为6组,第组的频数分别为10,14,16,20,
第6组的频数为:.
故选:A.
直接利用频数与频率的关系得出第5组的频数,进而得出答案.
此题主要考查了频数与频率,正确得出第5组频数是解题关键.
5.【答案】B
【解析】
【分析】
本题考查了频数和频率,解答本题的关键是掌握频率先求出其余情况出现的频率,然后根据频率求解.
【解答】
解:其余情况出现的频率,
则这次调查的总数.
故选B.
6.【答案】D
【解析】解:“早”字出现的频率是:,
故选:D.
利用频率的计算方法计算即可.
此题主要考查了频率,关键是掌握频率频数总数.
7.【答案】A
【解析】
【分析】
本题考查的是对频数的灵活运用,了解基本概念是解决本题的关键根据各小组频数之和等于数据总和;可得答案.
【解答】
解:根据频数的概念,各小组频数之和等于数据总和,即n;
故选A.
8.【答案】D
【解析】
【分析】
本题主要考查频率直方图的定义及学生对其的准备理解.频率直方图是按照数据从小到大的顺序排列,包括所有的数据,即数据的变化范围是指数据的最大值和最小值的差.
【解答】
解:数据的变动范围是指数据的最大值与最小值的差.
故选D.
9.【答案】D
【解析】解:全班学生数为人,此结论正确;
由频数分布表可知,组距为,组数为7组,故均正确;
跳绳次数在范围的学生占全班学生的,故此结论正确;
故选:D.
将各组频数相加即可得;由频率分布表即可知组数和组距;将范围的两组频数相加,再将其除以总人数即可得百分比.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力.读图时要全面细致,同时,解题方法要灵活多样,切忌死记硬背.
10.【答案】C
【解析】
【分析】
此题考查了频数率分布表,熟练掌握频数、频率与总数之间的关系是解题的关键.根据的频数和频率求出抽取的总数,再根据频率频数总数求出a即可.
【解答】
解:抽取的样本总数为,
.
故选C.
11.【答案】
【解析】解:个数据分布在5个组内,第一、二、四、五组的频数分别为9,16,40,15,
第三组数据的频数为20,
第三组对应的扇形圆心角的度数为,
故答案为:.
先根据题意,得到第三组数据的频数,再根据扇形圆心角计算公式进行计算即可.
本题主要考查了扇形统计图的应用,解题时注意:用整个圆的面积表示总数单位,用圆的扇形面积表示各部分占总数的百分数.
12.【答案】8
【解析】
【分析】
此题考查了频数率分布直方图,要知道,频数分布直方图中各个长方形的高之比即为各组频数之比.频数分布直方图中,各个长方形的高之比依次为2:3:4:1,则指各组频数之比为2:3:4:1,据此即可求出第四小组的频数.
【解答】
解:第四小组的频数:.
故答案为8.
13.【答案】
【解析】解:4出现的频率是.
故答案为:.
用4出现的次数除以数据的个数即可.
本题考查了频数与频率:频数是指每个对象出现的次数.频率是指每个对象出现的次数与总次数的比值或者百分比,即频率频数总数.
14.【答案】
【解析】解:根据题意,得:
频率.
故答案为.
根据频率公式作答即可.
本题是对频率、频数灵活运用的综合考查.熟练运用公式频率作答即可.
15.【答案】解:频数分布表如下:
分组
划记
频数
?
正正一
11
?
正正正止
19
?
13
正
5
2
合计
50
频数分布直方图如下:
从直方图可以看出:居民月平均用水量大部分在至之间;居民月平均用水量在范围内的最多,有19户;
要使的家庭收费不受影响,你觉得家庭月均用水量应该定为5吨,因为月平均用水量不超过5吨的有30户,.
【解析】本题考查读频数分布直方图和频数分布表的能力及利用统计图表获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
根据题中给出的50个数据,从中分别找出与??的个数,进行划记,得到对应的频数,进而完成频数分布表和频数分布直方图;
本题答案不唯一.例如:从直方图可以看出:居民月平均用水量大部分在至之间;居民月平均用水量在范围内的最多,有19户;
由于,所以为了鼓励节约用水,要使的家庭收费不受影响,即要使30户的家庭收费不受影响,而,故家庭月均用水量应该定为5吨.
16.【答案】解:名,?
名,
频数分布直方图如图:
答:在这次调查中共调查了500名学生;
名;
答:大约有8000名学生能达到教育行政部门规定的户外活动时间.
【解析】本题主要考查了条形统计图,扇形统计图及用样本估计总体,解题的关键是读懂统计图,能正确的从统计图中获取信息.
由1小时的人数及其百分比可得总人数,求得小时的人数,作图即可;
用总人数乘以样本的百分比可得答案.
17.【答案】解:;
;
画图如下:
;
根据题意,50人中日行走步数不低于万步的总人数为人,
所占比例为,
答:在被抽查的教师中,“运动达人”出现的频率为.
【解析】此题考查了频数分布直方图,扇形统计图,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
由B组人数及其所占百分比可得被调查的总人数;
从图中获取a,b的值,然后便可得出c,再补全频数分布直方图即可;
用乘以D组人数占被调查人数的比例即可得出结果;
先得出50人中日行走步数不低于万步的总人数为人,便可得出结果.
【解答】
解:本次抽查的教师人数是:人,
故答案为50人;
从图中可知,,,
,
频数分布直方图见答案,
故答案为2;
组所对应的扇形圆心角度数为,
故答案案为;
见答案.
18.【答案】解:,,.
补全频数分布直方图如图所示.
成绩在“”所在扇形的圆心角的度数为:.
【解析】略
第2页,共2页
第1页,共1页
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
