_山东省泰安市肥城市2020——2021学年九年级上学期期中数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | _山东省泰安市肥城市2020——2021学年九年级上学期期中数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 464.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 10:50:50 | ||
图片预览

文档简介
2020-2021学年山东省泰安市肥城市九年级(上)期中数学试卷(五四学制)
一、选择题(本大题共12个小题,满分48分,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得4分,错选、不选或选出的答案超过一个,均记零分.)
1.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A.2:3 B.2:5 C.3:5 D.3:2
2.如图,在Rt△ABC中,∠C=90°,AB=2BC,则sinB的值为( )
A. B. C. D.1
3.已知:如图,在⊙O中,OA⊥BC,∠AOB=70°,则∠ADC的度数为( )
A.30° B.35° C.45° D.70°
4.下列各组图形有可能不相似的是( )
A.各有一个角是50°的两个等腰三角形
B.各有一个角是100°的两个等腰三角形
C.各有一个角是50°的两个直角三角形
D.两个等腰直角三角形
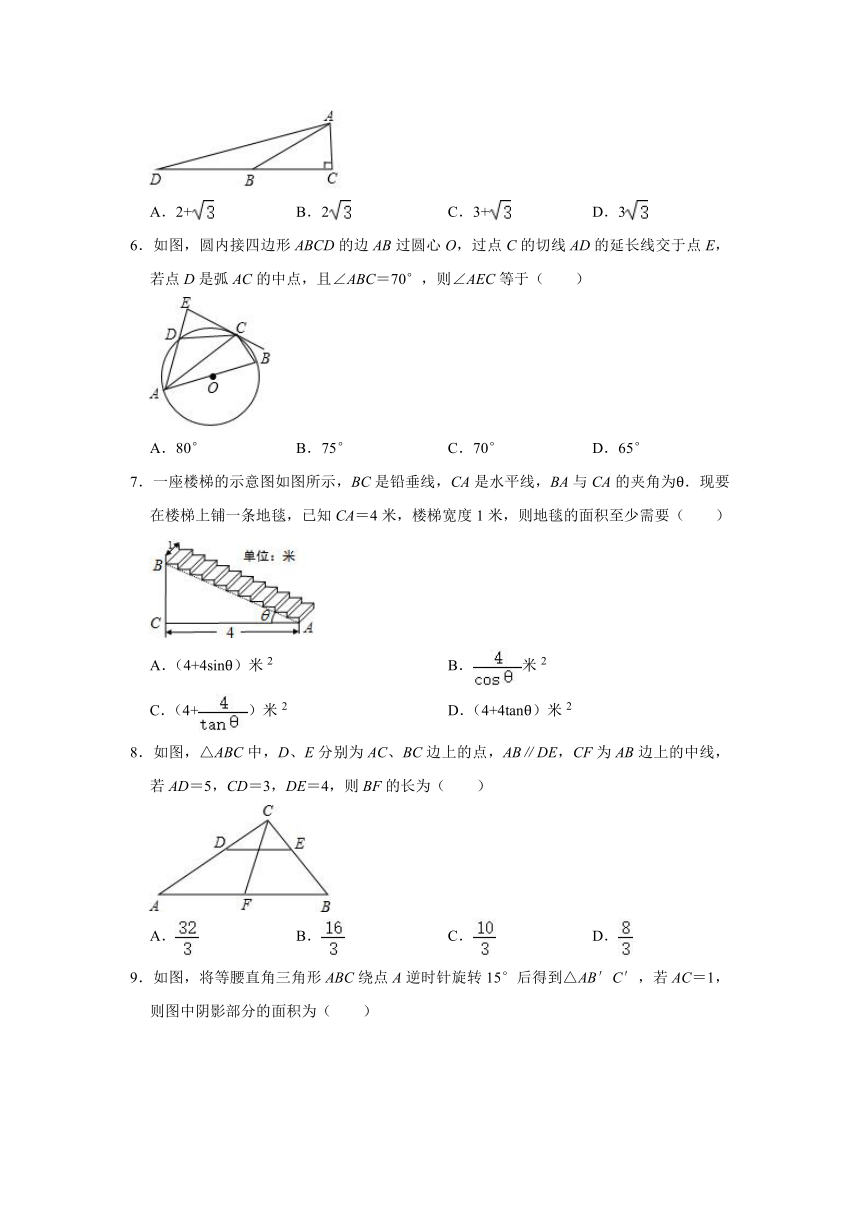
5.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )
A.2+ B.2 C.3+ D.3
6.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线AD的延长线交于点E,若点D是弧AC的中点,且∠ABC=70°,则∠AEC等于( )
A.80° B.75° C.70° D.65°
7.一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
A.(4+4sinθ)米2 B.米2
C.(4+)米2 D.(4+4tanθ)米2
8.如图,△ABC中,D、E分别为AC、BC边上的点,AB∥DE,CF为AB边上的中线,若AD=5,CD=3,DE=4,则BF的长为( )
A. B. C. D.
9.如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为( )
A. B. C. D.
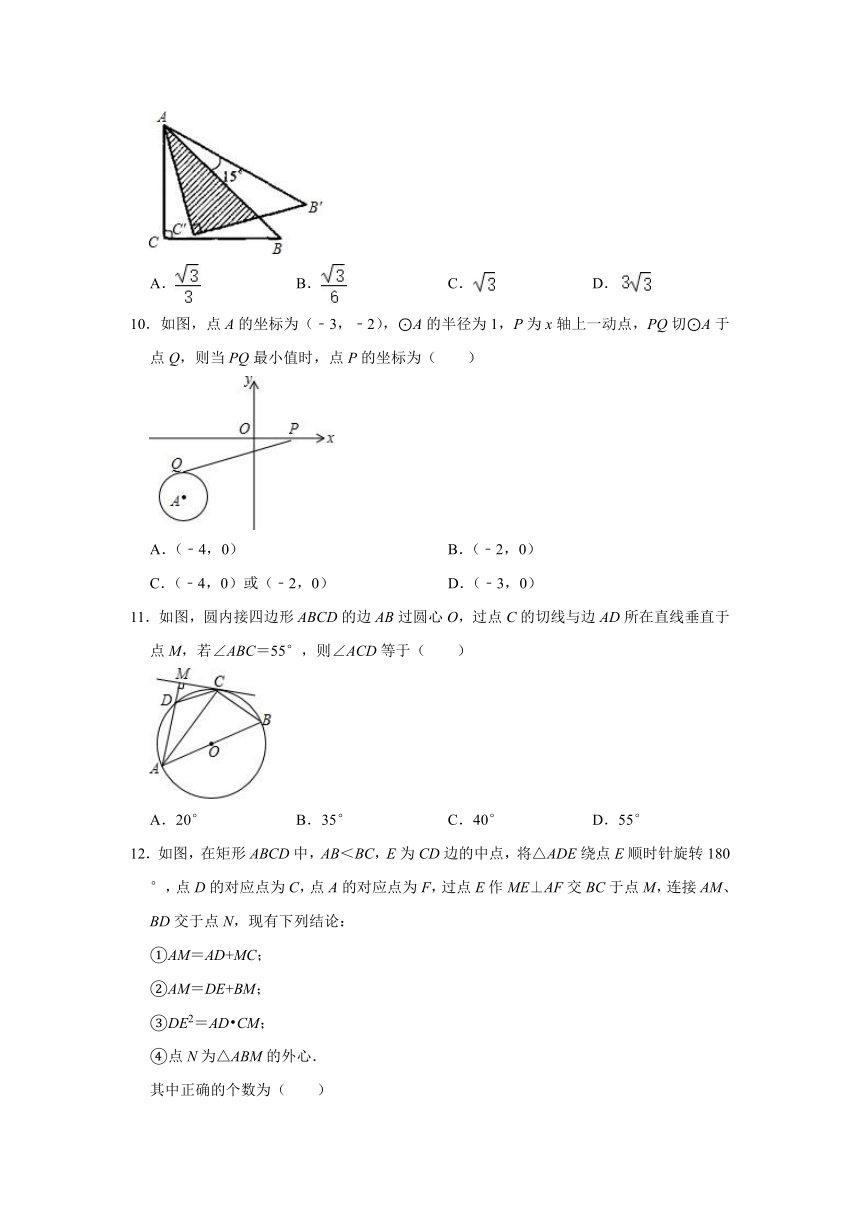
10.如图,点A的坐标为(﹣3,﹣2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小值时,点P的坐标为( )
A.(﹣4,0) B.(﹣2,0)
C.(﹣4,0)或(﹣2,0) D.(﹣3,0)
11.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )
A.20° B.35° C.40° D.55°
12.如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
①AM=AD+MC;
②AM=DE+BM;
③DE2=AD?CM;
④点N为△ABM的外心.
其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6小题;满分18分.只要求填写最后结果,每小题填对得4分)
13.在△ABC中,若∠A、∠B满足|cosA﹣|+(sinB﹣)2=0,则∠C= .
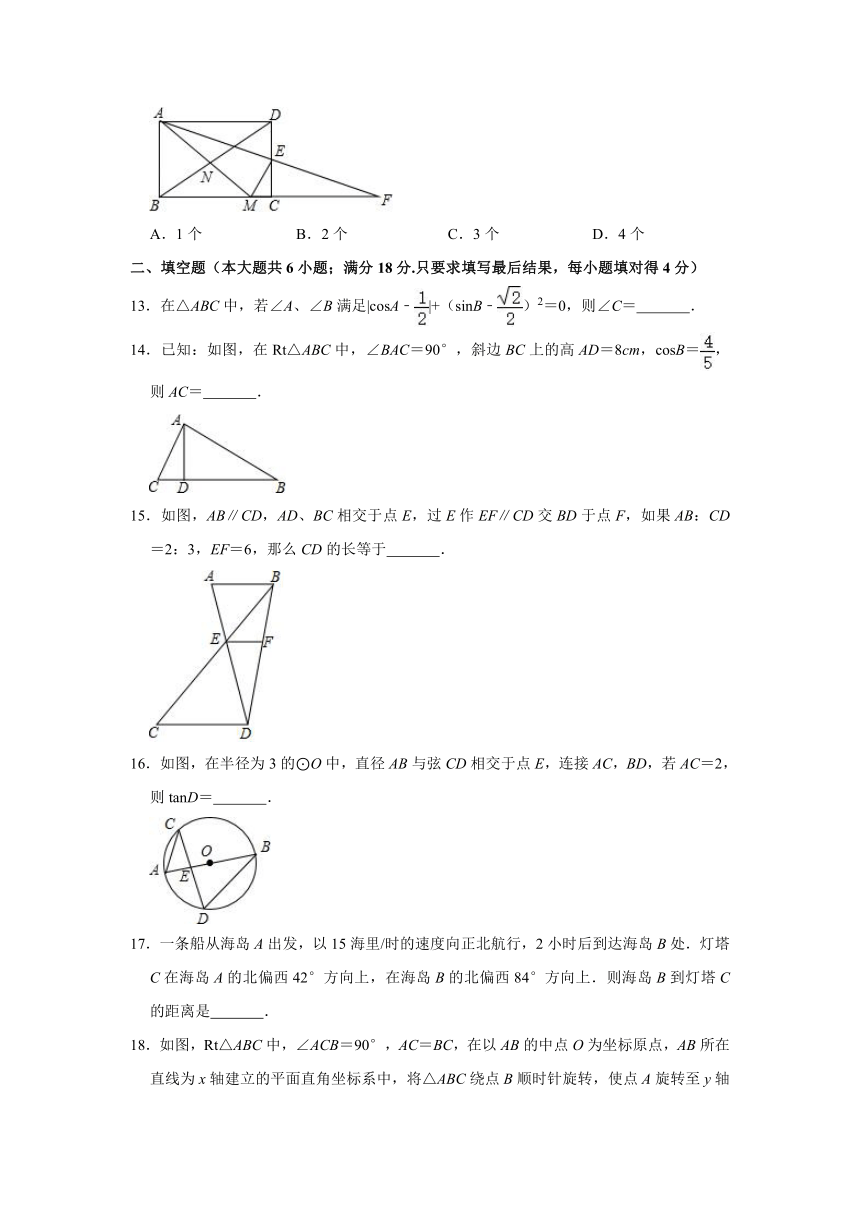
14.已知:如图,在Rt△ABC中,∠BAC=90°,斜边BC上的高AD=8cm,cosB=,则AC= .
15.如图,AB∥CD,AD、BC相交于点E,过E作EF∥CD交BD于点F,如果AB:CD=2:3,EF=6,那么CD的长等于 .
16.如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tanD= .
17.一条船从海岛A出发,以15海里/时的速度向正北航行,2小时后到达海岛B处.灯塔C在海岛A的北偏西42°方向上,在海岛B的北偏西84°方向上.则海岛B到灯塔C的距离是 .
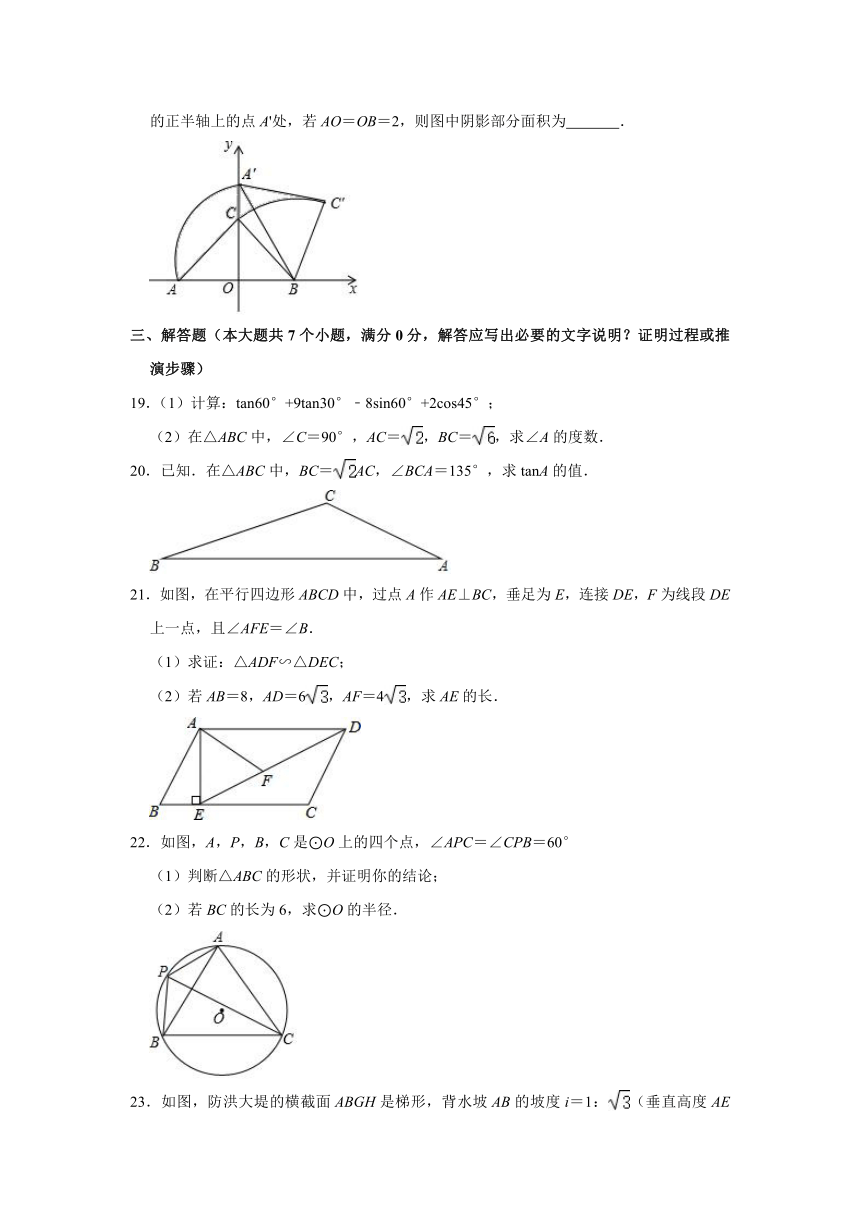
18.如图,Rt△ABC中,∠ACB=90°,AC=BC,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的点A'处,若AO=OB=2,则图中阴影部分面积为 .
三、解答题(本大题共7个小题,满分0分,解答应写出必要的文字说明?证明过程或推演步骤)
19.(1)计算:tan60°+9tan30°﹣8sin60°+2cos45°;
(2)在△ABC中,∠C=90°,AC=,BC=,求∠A的度数.
20.已知.在△ABC中,BC=AC,∠BCA=135°,求tanA的值.
21.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
22.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°
(1)判断△ABC的形状,并证明你的结论;
(2)若BC的长为6,求⊙O的半径.
23.如图,防洪大堤的横截面ABGH是梯形,背水坡AB的坡度i=1:(垂直高度AE与水平宽度BE的比),AB=20米,BC=30米,身高为1.7米的小明(AM=1.7米)站在大堤A点(M,A,E三点在同一条直线上),测得电线杆顶端D的仰角∠α=20°.
(1)求∠ABC;
(2)求电线杆CD的高度.(结果精确到个位,参考数据sin20°≈0.3,cos20°≈0.9,tan20°≈0.4,≈1.7)
24.从三角形(不是等腰三角形)一个顶点引起一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,∠A=48°,CD是△ABC的完美分割线,且AD=CD,求∠ACB的度数.
(2)如图2,在△ABC中,AC=2,BC=,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,找出CD与BD的关系.
25.如图,AB是⊙O的直径,点C是⊙O上一点(与点A,B不重合),过点C作直线PQ,使得∠ACQ=∠ABC.
(1)求证:直线PQ是⊙O的切线.
(2)过点A作AD⊥PQ于点D,交⊙O于点E,若⊙O的半径为2,sin∠DAC=,求图中阴影部分的面积.
附加题(本题供有兴趣的同学选做,不计入总分)
26.如图,在△ABC中,AM与BN相交于D,BM=3MC,AD=DM,求:
(1)BD:DN的值;
(2)面积S△ABN:S△CBN的值.
2020-2021学年山东省泰安市肥城市九年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一.选择题(共12小题)
1.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A.2:3 B.2:5 C.3:5 D.3:2
【分析】先根据平行四边形的性质及相似三角形的判定定理得出△DEF∽△BAF,再根据S△DEF:S△ABF=4:10:25即可得出其相似比,由相似三角形的性质即可求出的值,由AB=CD即可得出结论.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EAB=∠DEF,∠AFB=∠DFE,
∴△DEF∽△BAF,
∵S△DEF:S△ABF=4:25,
∴=,
∵AB=CD,
∴DE:EC=2:3.
故选:A.
2.如图,在Rt△ABC中,∠C=90°,AB=2BC,则sinB的值为( )
A. B. C. D.1
【分析】根据AB=2BC直接求sinB的值即可.
【解答】解:∵Rt△ABC中,∠C=90°,AB=2BC,
∴sinA===;
∴∠A=30°
∴∠B=60°
∴sinB=
故选:C.
3.已知:如图,在⊙O中,OA⊥BC,∠AOB=70°,则∠ADC的度数为( )
A.30° B.35° C.45° D.70°
【分析】先根据垂径定理得出=,再由圆周角定理即可得出结论.
【解答】解:∵OA⊥BC,∠AOB=70°,
∴=,
∴∠ADC=∠AOB=35°.
故选:B.
4.下列各组图形有可能不相似的是( )
A.各有一个角是50°的两个等腰三角形
B.各有一个角是100°的两个等腰三角形
C.各有一个角是50°的两个直角三角形
D.两个等腰直角三角形
【分析】分别利用相似三角形的判定方法,结合内角度数以及等腰三角形的性质判断即可.
【解答】解:A、各有一个角是50°的两个等腰三角形,有可能是一个为顶角,另一个为底角,这两个不相似,故此选项符合题意;
B、各有一个角是100°的两个等腰三角形,此角必为顶角,则底角都为40°,这两个三角形必相似,故此选项不合题意;
C、各有一个角是50°的两个直角三角形,再利用两直角,即可得出,这两个三角形必相似,故此选项不合题意;
D、两个等腰直角三角形,两角对应相等,这两个三角形必相似,故此选项不合题意;
故选:A.
5.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )
A.2+ B.2 C.3+ D.3
【分析】通过解直角△ABC得到AC与BC、AB间的数量关系,然后利用锐角三角函数的定义求tan∠DAC的值.
【解答】解:如图,∵在△ABC中,AC⊥BC,∠ABC=30°,
∴AB=2AC,BC==AC.
∵BD=BA,
∴DC=BD+BC=(2+)AC,
∴tan∠DAC===2+.
故选:A.
6.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线AD的延长线交于点E,若点D是弧AC的中点,且∠ABC=70°,则∠AEC等于( )
A.80° B.75° C.70° D.65°
【分析】由圆内接四边形的性质求出∠ADC=180°﹣∠ABC=125°,由圆周角定理求出∠ACB=90°,得出∠BAC=35°,由弦切角定理得出∠ECA,根据三角形内角和定理求出即可.
【解答】解:∵AB为⊙O的直径,
∴∠ACB=90°,
∵圆内接四边形ABCD的边AB过圆心O,
∴∠ADC+∠ABC=180°,
∵∠ABC=70°,
∴∠ADC=180°﹣∠ABC=110°,
∵D为的中点,
∴AD=DC,
∴∠EAC=∠DCA=×(180°﹣110°)=35°,
∵EC为⊙O的切线,
∴∠ECA=∠ABC=70°,
∴∠AEC=180°﹣∠EAC﹣∠ECA=180°﹣35°﹣70°=75°,
故选:B.
7.一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
A.(4+4sinθ)米2 B.米2
C.(4+)米2 D.(4+4tanθ)米2
【分析】由三角函数表示出BC,得出AC+BC的长度,由矩形的面积即可得出结果.
【解答】解:在Rt△ABC中,BC=AC?tanθ=4tanθ(米),
∴AC+BC=4+4tanθ(米),
∴地毯的面积至少需要1×(4+4tanθ)=4+4tanθ(米2);
故选:D.
8.如图,△ABC中,D、E分别为AC、BC边上的点,AB∥DE,CF为AB边上的中线,若AD=5,CD=3,DE=4,则BF的长为( )
A. B. C. D.
【分析】由AB∥DE可得△CDE∽△CAB,再由AD=5,CD=3,DE=4,可求AB的长.又CF为AB边上的中线,则F为AB的中点,问题可求.
【解答】解:∵AB∥DE,
∴△CDE∽△CAB,
∵AD=5,CD=3,DE=4,
∴AC=CD+AD=8,
∴,
∴AB=;
又CF为AB边上的中线,
∴F为AB的中点.
∴BF==.
故选:B.
9.如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为( )
A. B. C. D.
【分析】根据旋转的性质可得AC′=AC,∠BAC′=30°,然后利用∠BAC′的正切求出C′D的长度,再利用三角形的面积公式列式计算即可求解.
【解答】解:根据题意,AC′=AC=1,
∵∠B′AB=15°,
∴∠BAC′=45°﹣15°=30°,
∴C′D=AC′tan30°=,
∴S阴影=AC′?C′D=×1×=.
故选:B.
10.如图,点A的坐标为(﹣3,﹣2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小值时,点P的坐标为( )
A.(﹣4,0) B.(﹣2,0)
C.(﹣4,0)或(﹣2,0) D.(﹣3,0)
【分析】连结AQ、AP,由切线的性质可知AQ⊥QP,由勾股定理可知QP=,故此当AP有最小值时,PQ最短,根据垂线段最短可得到点P的坐标.
【解答】解:连接AQ,AP.
根据切线的性质定理,得AQ⊥PQ;
要使PQ最小,只需AP最小,
根据垂线段最短,可知当AP⊥x轴时,AP最短,
∴P点的坐标是(﹣3,0).
故选:D.
11.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )
A.20° B.35° C.40° D.55°
【分析】由圆内接四边形的性质求出∠ADC=180°﹣∠ABC=125°,由圆周角定理求出∠ACB=90°,得出∠BAC=35°,由弦切角定理得出∠MCA=∠ABC=55°,由三角形的外角性质得出∠DCM=∠ADC﹣∠AMC=35°,即可求出∠ACD的度数.
【解答】解:∵圆内接四边形ABCD的边AB过圆心O,
∴∠ADC+∠ABC=180°,∠ACB=90°,
∴∠ADC=180°﹣∠ABC=125°,∠BAC=90°﹣∠ABC=35°,
∵过点C的切线与边AD所在直线垂直于点M,
∴∠MCA=∠ABC=55°,∠AMC=90°,
∵∠ADC=∠AMC+∠DCM,
∴∠DCM=∠ADC﹣∠AMC=35°,
∴∠ACD=∠MCA﹣∠DCM=55°﹣35°=20°;
故选:A.
12.如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
①AM=AD+MC;
②AM=DE+BM;
③DE2=AD?CM;
④点N为△ABM的外心.
其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
【分析】根据全等三角形的性质以及线段垂直平分线的性质,即可得出AM=MC+AD;根据△ABG∽△ADE,且AB<BC,即可得出BG<DE,再根据AM=GM=BG+BM,即可得出AM=DE+BM不成立;根据ME⊥FF,EC⊥MF,运用射影定理即可得出EC2=CM×CF,据此可得DE2=AD?CM成立;根据N不是AM的中点,可得点N不是△ABM的外心.
【解答】解:∵E为CD边的中点,
∴DE=CE,
又∵∠D=∠ECF=90°,∠AED=∠FEC,
∴△ADE≌△FCE,
∴AD=CF,AE=FE,
又∵ME⊥AF,
∴ME垂直平分AF,
∴AM=MF=MC+CF,
∴AM=MC+AD,故①正确;
如图,延长CB至G,使得∠BAG=∠DAE,
由AM=MF,AD∥BF,可得∠DAE=∠F=∠EAM,
可设∠BAG=∠DAE=∠EAM=α,∠BAM=β,则∠AED=∠EAB=∠GAM=α+β,
由∠BAG=∠DAE,∠ABG=∠ADE=90°,可得△ABG∽△ADE,
∴∠G=∠AED=α+β,
∴∠G=∠GAM,
∴AM=GM=BG+BM,
由△ABG∽△ADE,可得=,
而AB<BC=AD,
∴BG<DE,
∴BG+BM<DE+BM,
即AM<DE+BM,
∴AM=DE+BM不成立,故②错误;
∵ME⊥FF,EC⊥MF,
∴EC2=CM×CF,
又∵EC=DE,AD=CF,
∴DE2=AD?CM,故③正确;
∵∠ABM=90°,
∴AM是△ABM的外接圆的直径,
∵BM<AD,
∴当BM∥AD时,=<1,
∴N不是AM的中点,
∴点N不是△ABM的外心,故④错误.
综上所述,正确的结论有2个,
故选:B.
二.填空题(共6小题)
13.在△ABC中,若∠A、∠B满足|cosA﹣|+(sinB﹣)2=0,则∠C= 75° .
【分析】首先根据绝对值与偶次幂具有非负性可知cosA﹣=0,sinB﹣=0,然后根据特殊角的三角函数值得到∠A、∠B的度数,再根据三角形内角和为180°算出∠C的度数即可.
【解答】解:∵|cosA﹣|+(sinB﹣)2=0,
∴cosA﹣=0,sinB﹣=0,
∴cosA=,sinB=,
∴∠A=60°,∠B=45°,
则∠C=180°﹣∠A﹣∠B=180°﹣60°﹣45°=75°,
故答案为:75°.
14.已知:如图,在Rt△ABC中,∠BAC=90°,斜边BC上的高AD=8cm,cosB=,则AC= 10cm .
【分析】先利用等角的余角相等证明∠B=∠CAD,然后在Rt△ACD中利用∠CAD的余弦求AC的长.
【解答】解:∵AD为高,
∴∠ADB=90°,
∴∠B+∠DAB=90°,
∵∠CAD+∠DAB=90°,
∴∠B=∠CAD,
∴cos∠CAD=cosB=,
在Rt△ACD中,∵cos∠CAD=,
∴AC==10(cm).
故答案为10cm.
15.如图,AB∥CD,AD、BC相交于点E,过E作EF∥CD交BD于点F,如果AB:CD=2:3,EF=6,那么CD的长等于 15 .
【分析】由△ABE∽△DCE,推出==,可得=,再证明△BEF∽△BCD,可得==,由此即可解决问题.
【解答】解:∵AB∥CD,
∴△ABE∽△DCE,
∴==,
∴=,
∵EF∥CD,
∴△BEF∽△BCD,
∴==,
∵EF=6,
∴CD=15,
故答案为15.
16.如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tanD= 2 .
【分析】连接BC可得RT△ACB,由勾股定理求得BC的长,进而由tanD=tanA=可得答案.
【解答】解:如图,连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=6,AC=2,
∴BC===4,
又∵∠D=∠A,
∴tanD=tanA===2.
故答案为:2.
17.一条船从海岛A出发,以15海里/时的速度向正北航行,2小时后到达海岛B处.灯塔C在海岛A的北偏西42°方向上,在海岛B的北偏西84°方向上.则海岛B到灯塔C的距离是 30海里 .
【分析】根据三角形的外角性质求出∠C,进而得到∠C=∠CAB,根据等腰三角形的判定定理得到BC=AB,根据题意计算,得到答案.
【解答】解:根据题意得:∠CBD=84°,∠CAB=42°,
∴∠C=∠CBD﹣∠CAB=42°,
∴∠C=∠CAB,
∴BC=AB,
∵AB=15×2=30(海里),
∴BC=30(海里),
即海岛B到灯塔C的距离是30海里,
故答案为:30海里.
18.如图,Rt△ABC中,∠ACB=90°,AC=BC,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的点A'处,若AO=OB=2,则图中阴影部分面积为 .
【分析】根据等腰直角三角形的性质求出AB,再根据旋转的性质可得A′B=AB,然后求出∠OA′B=30°,再根据直角三角形两锐角互余求出∠A′BA=60°,即旋转角为60°,再根据S阴影=S扇形ABA′+S△A′BC′﹣S△ABC﹣S扇形CBC′=S扇形ABA′﹣S扇形CBC′,然后利用扇形的面积公式列式计算即可得解.
【解答】解:∵∠ACB=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴AB=2OA=2OB=4,BC=2,
∵△ABC绕点B顺时针旋转点A在A′处,
∴BA′=AB,
∴BA′=2OB,
∴∠OA′B=30°,
∴∠A′BA=60°,
即旋转角为60°,
S阴影=S扇形ABA′+S△A′BC′﹣S△ABC﹣S扇形CBC′
=S扇形ABA′﹣S扇形CBC′
=
=.
故答案为:.
三.解答题
19.(1)计算:tan60°+9tan30°﹣8sin60°+2cos45°;
(2)在△ABC中,∠C=90°,AC=,BC=,求∠A的度数.
【分析】(1)代入特殊锐角的三角函数值进行计算即可;
(2)由锐角三角函数定义的定义得tanA==,即可得出答案.
【解答】解:(1)tan60°+9tan30°﹣8sin60°+2cos45°
=+9×﹣8×+2×
=+3﹣4+
=;
(2)∵∠C=90°,AC=,BC=,
∴tanA===,
∴∠A=60°.
20.已知.在△ABC中,BC=AC,∠BCA=135°,求tanA的值.
【分析】过B点作BD⊥AC交AC的延长线于D点,根据等腰直角三角形的性质得到BD=CD=BC,根据正切的定义计算即可.
【解答】解:过B点作BD⊥AC交AC的延长线于D点,
则∠BCD=45,
∴BD=CD=BC,
设AC=k,则BD=CD=k,AD=2k,
tanA==.
21.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
【分析】(1)根据四边形ABCD为平行四边形,利用平行四边形的对边平行且相等,得到一对同旁内角互补,一对内错角相等,根据已知角相等,利用等角的补角相等得到两组对应角相等,从而推知:△ADF∽△DEC;
(2)由△ADF∽△DEC,得比例,求出DE的长.利用勾股定理求出AE的长.
【解答】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
∴△ADF∽△DEC.
(2)解:∵四边形ABCD是平行四边形,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴=,
∴DE===12.
在Rt△ADE中,由勾股定理得:AE==6.
22.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°
(1)判断△ABC的形状,并证明你的结论;
(2)若BC的长为6,求⊙O的半径.
【分析】(1)根据圆周角定理得到∠ABC=∠APC=60°,∠CAB=∠CPB=60°,根据等边三角形的判定定理证明;
(2)延长BO交⊙O于E,连接CE,根据圆周角定理得到∠E=∠BAC=60°,根据正弦的概念计算即可.
【解答】解:(1)△ABC是等边三角形,
理由如下:由圆周角定理得,∠ABC=∠APC=60°,∠CAB=∠CPB=60°,
∴△ABC是等边三角形;
(2)延长BO交⊙O于E,连接CE,
由圆周角定理得,∠E=∠BAC=60°,
∴BE==4,
∴⊙O的半径为2.
23.如图,防洪大堤的横截面ABGH是梯形,背水坡AB的坡度i=1:(垂直高度AE与水平宽度BE的比),AB=20米,BC=30米,身高为1.7米的小明(AM=1.7米)站在大堤A点(M,A,E三点在同一条直线上),测得电线杆顶端D的仰角∠α=20°.
(1)求∠ABC;
(2)求电线杆CD的高度.(结果精确到个位,参考数据sin20°≈0.3,cos20°≈0.9,tan20°≈0.4,≈1.7)
【分析】(1)由tan∠ABE=i=1:,得出∠ABE=30°,即可得出结果;
(2)过M点作MN垂直于CD的于点N,含30°角直角三角形的性质得出AE=AB=10,由三角函数定义得出BE=ABcos30°=10,则CN=AE+AM=11.7,MN=CB+BE=30+10,求出DN=MNtan20°=12+4,即可得出结果.
【解答】解:(1)∵i=1:,
∴tan∠ABE=i=1:,
∴∠ABE=30°,
∴∠ABC=150°;
(2)过M点作MN垂直于CD的于点N,如图所示:
∵AB=20m,∠ABE=30°,
∴AE=AB=×20=10,
BE=ABcos30°=20×=10,
∴CN=AE+AM=10+1.7=11.7,
MN=CB+BE=30+10,
∵∠NMD=20°,MN=30+10,
∴DN=MNtan20°=(30+10)×0.4=12+4,
∴CD=CN+DN=11.7+12+4=23.7+4≈31.
答:电线杆CD的高度约为31米.
24.从三角形(不是等腰三角形)一个顶点引起一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,∠A=48°,CD是△ABC的完美分割线,且AD=CD,求∠ACB的度数.
(2)如图2,在△ABC中,AC=2,BC=,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,找出CD与BD的关系.
【分析】(1)根据相似三角形的性质得到∠BCD=∠A=48°,再根据角的和差关系求出∠ACB即可.
(2)利用△BCD∽△BAC,得=,可得结论.
【解答】解:(1)当AD=CD时,如图3,∠ACD=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=96°.
(2)结论:CD=BD.
∵△BCD∽△BAC,
∵△BCD∽△BAC,
∴=,
∴==,
∴CD=BD.
25.如图,AB是⊙O的直径,点C是⊙O上一点(与点A,B不重合),过点C作直线PQ,使得∠ACQ=∠ABC.
(1)求证:直线PQ是⊙O的切线.
(2)过点A作AD⊥PQ于点D,交⊙O于点E,若⊙O的半径为2,sin∠DAC=,求图中阴影部分的面积.
【分析】(1)连接OC,由直径所对的圆周角为直角,可得∠ACB=90°;利用等腰三角形的性质及已知条件∠ACQ=∠ABC,可求得∠OCQ=90°,按照切线的判定定理可得结论.
(2)由sin∠DAC=,可得∠DAC=30°,从而可得∠ACD的 度数,进而判定△AEO为等边三角形,则∠AOE的度数可得;利用S阴影=S扇形﹣S△AEO,可求得答案.
【解答】解:(1)证明:如图,连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵OA=OC,
∴∠CAB=∠ACO.
∵∠ACQ=∠ABC,
∴∠CAB+∠ABC=∠ACO+∠ACQ=∠OCQ=90°,即OC⊥PQ,
∴直线PQ是⊙O的切线.
(2)连接OE,
∵sin∠DAC=,AD⊥PQ,
∴∠DAC=30°,∠ACD=60°.
∴∠ABC=∠ACD=60°,
∴∠CAB=90°﹣60°=30°,
∴∠EAO=∠DAC+∠CAB=60°,
又∵OA=OE,
∴△AEO为等边三角形,
∴∠AOE=60°.
∴S阴影=S扇形﹣S△AEO
=S扇形﹣OA?OE?sin60°
=×22﹣×2×2×
=﹣.
∴图中阴影部分的面积为﹣.
26.如图,在△ABC中,AM与BN相交于D,BM=3MC,AD=DM,求:
(1)BD:DN的值;
(2)面积S△ABN:S△CBN的值.
【分析】(1)过C作CE∥AM交BA延长线于点E,延长BN交CE于点F,根据相似三角形的性质和平行线分线段成比例定理计算;
(2)根据两三角形高相等,则底边的比等于面积比计算.
【解答】解:(1)过C作CE∥AM交BA延长线于点E,延长BN交CE于点F.
∵CE∥AM,
∴∠DAN=∠FCN,∠ADN=∠CFN,
∴△DAN∽△FCN,
∴=,
又∵AD=DM,
∴=,
∵CE∥AM,
∴===,
∴=,
∴BD:DN=3:=7:1.
(2)由(1)得:△DAN相似于△FCN,
∴==
∴S△ABN:S△CBN=AN:CN=3:4.
一、选择题(本大题共12个小题,满分48分,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得4分,错选、不选或选出的答案超过一个,均记零分.)
1.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A.2:3 B.2:5 C.3:5 D.3:2
2.如图,在Rt△ABC中,∠C=90°,AB=2BC,则sinB的值为( )
A. B. C. D.1
3.已知:如图,在⊙O中,OA⊥BC,∠AOB=70°,则∠ADC的度数为( )
A.30° B.35° C.45° D.70°
4.下列各组图形有可能不相似的是( )
A.各有一个角是50°的两个等腰三角形
B.各有一个角是100°的两个等腰三角形
C.各有一个角是50°的两个直角三角形
D.两个等腰直角三角形
5.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )
A.2+ B.2 C.3+ D.3
6.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线AD的延长线交于点E,若点D是弧AC的中点,且∠ABC=70°,则∠AEC等于( )
A.80° B.75° C.70° D.65°
7.一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
A.(4+4sinθ)米2 B.米2
C.(4+)米2 D.(4+4tanθ)米2
8.如图,△ABC中,D、E分别为AC、BC边上的点,AB∥DE,CF为AB边上的中线,若AD=5,CD=3,DE=4,则BF的长为( )
A. B. C. D.
9.如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为( )
A. B. C. D.
10.如图,点A的坐标为(﹣3,﹣2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小值时,点P的坐标为( )
A.(﹣4,0) B.(﹣2,0)
C.(﹣4,0)或(﹣2,0) D.(﹣3,0)
11.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )
A.20° B.35° C.40° D.55°
12.如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
①AM=AD+MC;
②AM=DE+BM;
③DE2=AD?CM;
④点N为△ABM的外心.
其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6小题;满分18分.只要求填写最后结果,每小题填对得4分)
13.在△ABC中,若∠A、∠B满足|cosA﹣|+(sinB﹣)2=0,则∠C= .
14.已知:如图,在Rt△ABC中,∠BAC=90°,斜边BC上的高AD=8cm,cosB=,则AC= .
15.如图,AB∥CD,AD、BC相交于点E,过E作EF∥CD交BD于点F,如果AB:CD=2:3,EF=6,那么CD的长等于 .
16.如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tanD= .
17.一条船从海岛A出发,以15海里/时的速度向正北航行,2小时后到达海岛B处.灯塔C在海岛A的北偏西42°方向上,在海岛B的北偏西84°方向上.则海岛B到灯塔C的距离是 .
18.如图,Rt△ABC中,∠ACB=90°,AC=BC,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的点A'处,若AO=OB=2,则图中阴影部分面积为 .
三、解答题(本大题共7个小题,满分0分,解答应写出必要的文字说明?证明过程或推演步骤)
19.(1)计算:tan60°+9tan30°﹣8sin60°+2cos45°;
(2)在△ABC中,∠C=90°,AC=,BC=,求∠A的度数.
20.已知.在△ABC中,BC=AC,∠BCA=135°,求tanA的值.
21.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
22.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°
(1)判断△ABC的形状,并证明你的结论;
(2)若BC的长为6,求⊙O的半径.
23.如图,防洪大堤的横截面ABGH是梯形,背水坡AB的坡度i=1:(垂直高度AE与水平宽度BE的比),AB=20米,BC=30米,身高为1.7米的小明(AM=1.7米)站在大堤A点(M,A,E三点在同一条直线上),测得电线杆顶端D的仰角∠α=20°.
(1)求∠ABC;
(2)求电线杆CD的高度.(结果精确到个位,参考数据sin20°≈0.3,cos20°≈0.9,tan20°≈0.4,≈1.7)
24.从三角形(不是等腰三角形)一个顶点引起一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,∠A=48°,CD是△ABC的完美分割线,且AD=CD,求∠ACB的度数.
(2)如图2,在△ABC中,AC=2,BC=,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,找出CD与BD的关系.
25.如图,AB是⊙O的直径,点C是⊙O上一点(与点A,B不重合),过点C作直线PQ,使得∠ACQ=∠ABC.
(1)求证:直线PQ是⊙O的切线.
(2)过点A作AD⊥PQ于点D,交⊙O于点E,若⊙O的半径为2,sin∠DAC=,求图中阴影部分的面积.
附加题(本题供有兴趣的同学选做,不计入总分)
26.如图,在△ABC中,AM与BN相交于D,BM=3MC,AD=DM,求:
(1)BD:DN的值;
(2)面积S△ABN:S△CBN的值.
2020-2021学年山东省泰安市肥城市九年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一.选择题(共12小题)
1.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A.2:3 B.2:5 C.3:5 D.3:2
【分析】先根据平行四边形的性质及相似三角形的判定定理得出△DEF∽△BAF,再根据S△DEF:S△ABF=4:10:25即可得出其相似比,由相似三角形的性质即可求出的值,由AB=CD即可得出结论.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EAB=∠DEF,∠AFB=∠DFE,
∴△DEF∽△BAF,
∵S△DEF:S△ABF=4:25,
∴=,
∵AB=CD,
∴DE:EC=2:3.
故选:A.
2.如图,在Rt△ABC中,∠C=90°,AB=2BC,则sinB的值为( )
A. B. C. D.1
【分析】根据AB=2BC直接求sinB的值即可.
【解答】解:∵Rt△ABC中,∠C=90°,AB=2BC,
∴sinA===;
∴∠A=30°
∴∠B=60°
∴sinB=
故选:C.
3.已知:如图,在⊙O中,OA⊥BC,∠AOB=70°,则∠ADC的度数为( )
A.30° B.35° C.45° D.70°
【分析】先根据垂径定理得出=,再由圆周角定理即可得出结论.
【解答】解:∵OA⊥BC,∠AOB=70°,
∴=,
∴∠ADC=∠AOB=35°.
故选:B.
4.下列各组图形有可能不相似的是( )
A.各有一个角是50°的两个等腰三角形
B.各有一个角是100°的两个等腰三角形
C.各有一个角是50°的两个直角三角形
D.两个等腰直角三角形
【分析】分别利用相似三角形的判定方法,结合内角度数以及等腰三角形的性质判断即可.
【解答】解:A、各有一个角是50°的两个等腰三角形,有可能是一个为顶角,另一个为底角,这两个不相似,故此选项符合题意;
B、各有一个角是100°的两个等腰三角形,此角必为顶角,则底角都为40°,这两个三角形必相似,故此选项不合题意;
C、各有一个角是50°的两个直角三角形,再利用两直角,即可得出,这两个三角形必相似,故此选项不合题意;
D、两个等腰直角三角形,两角对应相等,这两个三角形必相似,故此选项不合题意;
故选:A.
5.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )
A.2+ B.2 C.3+ D.3
【分析】通过解直角△ABC得到AC与BC、AB间的数量关系,然后利用锐角三角函数的定义求tan∠DAC的值.
【解答】解:如图,∵在△ABC中,AC⊥BC,∠ABC=30°,
∴AB=2AC,BC==AC.
∵BD=BA,
∴DC=BD+BC=(2+)AC,
∴tan∠DAC===2+.
故选:A.
6.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线AD的延长线交于点E,若点D是弧AC的中点,且∠ABC=70°,则∠AEC等于( )
A.80° B.75° C.70° D.65°
【分析】由圆内接四边形的性质求出∠ADC=180°﹣∠ABC=125°,由圆周角定理求出∠ACB=90°,得出∠BAC=35°,由弦切角定理得出∠ECA,根据三角形内角和定理求出即可.
【解答】解:∵AB为⊙O的直径,
∴∠ACB=90°,
∵圆内接四边形ABCD的边AB过圆心O,
∴∠ADC+∠ABC=180°,
∵∠ABC=70°,
∴∠ADC=180°﹣∠ABC=110°,
∵D为的中点,
∴AD=DC,
∴∠EAC=∠DCA=×(180°﹣110°)=35°,
∵EC为⊙O的切线,
∴∠ECA=∠ABC=70°,
∴∠AEC=180°﹣∠EAC﹣∠ECA=180°﹣35°﹣70°=75°,
故选:B.
7.一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
A.(4+4sinθ)米2 B.米2
C.(4+)米2 D.(4+4tanθ)米2
【分析】由三角函数表示出BC,得出AC+BC的长度,由矩形的面积即可得出结果.
【解答】解:在Rt△ABC中,BC=AC?tanθ=4tanθ(米),
∴AC+BC=4+4tanθ(米),
∴地毯的面积至少需要1×(4+4tanθ)=4+4tanθ(米2);
故选:D.
8.如图,△ABC中,D、E分别为AC、BC边上的点,AB∥DE,CF为AB边上的中线,若AD=5,CD=3,DE=4,则BF的长为( )
A. B. C. D.
【分析】由AB∥DE可得△CDE∽△CAB,再由AD=5,CD=3,DE=4,可求AB的长.又CF为AB边上的中线,则F为AB的中点,问题可求.
【解答】解:∵AB∥DE,
∴△CDE∽△CAB,
∵AD=5,CD=3,DE=4,
∴AC=CD+AD=8,
∴,
∴AB=;
又CF为AB边上的中线,
∴F为AB的中点.
∴BF==.
故选:B.
9.如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为( )
A. B. C. D.
【分析】根据旋转的性质可得AC′=AC,∠BAC′=30°,然后利用∠BAC′的正切求出C′D的长度,再利用三角形的面积公式列式计算即可求解.
【解答】解:根据题意,AC′=AC=1,
∵∠B′AB=15°,
∴∠BAC′=45°﹣15°=30°,
∴C′D=AC′tan30°=,
∴S阴影=AC′?C′D=×1×=.
故选:B.
10.如图,点A的坐标为(﹣3,﹣2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小值时,点P的坐标为( )
A.(﹣4,0) B.(﹣2,0)
C.(﹣4,0)或(﹣2,0) D.(﹣3,0)
【分析】连结AQ、AP,由切线的性质可知AQ⊥QP,由勾股定理可知QP=,故此当AP有最小值时,PQ最短,根据垂线段最短可得到点P的坐标.
【解答】解:连接AQ,AP.
根据切线的性质定理,得AQ⊥PQ;
要使PQ最小,只需AP最小,
根据垂线段最短,可知当AP⊥x轴时,AP最短,
∴P点的坐标是(﹣3,0).
故选:D.
11.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )
A.20° B.35° C.40° D.55°
【分析】由圆内接四边形的性质求出∠ADC=180°﹣∠ABC=125°,由圆周角定理求出∠ACB=90°,得出∠BAC=35°,由弦切角定理得出∠MCA=∠ABC=55°,由三角形的外角性质得出∠DCM=∠ADC﹣∠AMC=35°,即可求出∠ACD的度数.
【解答】解:∵圆内接四边形ABCD的边AB过圆心O,
∴∠ADC+∠ABC=180°,∠ACB=90°,
∴∠ADC=180°﹣∠ABC=125°,∠BAC=90°﹣∠ABC=35°,
∵过点C的切线与边AD所在直线垂直于点M,
∴∠MCA=∠ABC=55°,∠AMC=90°,
∵∠ADC=∠AMC+∠DCM,
∴∠DCM=∠ADC﹣∠AMC=35°,
∴∠ACD=∠MCA﹣∠DCM=55°﹣35°=20°;
故选:A.
12.如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
①AM=AD+MC;
②AM=DE+BM;
③DE2=AD?CM;
④点N为△ABM的外心.
其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
【分析】根据全等三角形的性质以及线段垂直平分线的性质,即可得出AM=MC+AD;根据△ABG∽△ADE,且AB<BC,即可得出BG<DE,再根据AM=GM=BG+BM,即可得出AM=DE+BM不成立;根据ME⊥FF,EC⊥MF,运用射影定理即可得出EC2=CM×CF,据此可得DE2=AD?CM成立;根据N不是AM的中点,可得点N不是△ABM的外心.
【解答】解:∵E为CD边的中点,
∴DE=CE,
又∵∠D=∠ECF=90°,∠AED=∠FEC,
∴△ADE≌△FCE,
∴AD=CF,AE=FE,
又∵ME⊥AF,
∴ME垂直平分AF,
∴AM=MF=MC+CF,
∴AM=MC+AD,故①正确;
如图,延长CB至G,使得∠BAG=∠DAE,
由AM=MF,AD∥BF,可得∠DAE=∠F=∠EAM,
可设∠BAG=∠DAE=∠EAM=α,∠BAM=β,则∠AED=∠EAB=∠GAM=α+β,
由∠BAG=∠DAE,∠ABG=∠ADE=90°,可得△ABG∽△ADE,
∴∠G=∠AED=α+β,
∴∠G=∠GAM,
∴AM=GM=BG+BM,
由△ABG∽△ADE,可得=,
而AB<BC=AD,
∴BG<DE,
∴BG+BM<DE+BM,
即AM<DE+BM,
∴AM=DE+BM不成立,故②错误;
∵ME⊥FF,EC⊥MF,
∴EC2=CM×CF,
又∵EC=DE,AD=CF,
∴DE2=AD?CM,故③正确;
∵∠ABM=90°,
∴AM是△ABM的外接圆的直径,
∵BM<AD,
∴当BM∥AD时,=<1,
∴N不是AM的中点,
∴点N不是△ABM的外心,故④错误.
综上所述,正确的结论有2个,
故选:B.
二.填空题(共6小题)
13.在△ABC中,若∠A、∠B满足|cosA﹣|+(sinB﹣)2=0,则∠C= 75° .
【分析】首先根据绝对值与偶次幂具有非负性可知cosA﹣=0,sinB﹣=0,然后根据特殊角的三角函数值得到∠A、∠B的度数,再根据三角形内角和为180°算出∠C的度数即可.
【解答】解:∵|cosA﹣|+(sinB﹣)2=0,
∴cosA﹣=0,sinB﹣=0,
∴cosA=,sinB=,
∴∠A=60°,∠B=45°,
则∠C=180°﹣∠A﹣∠B=180°﹣60°﹣45°=75°,
故答案为:75°.
14.已知:如图,在Rt△ABC中,∠BAC=90°,斜边BC上的高AD=8cm,cosB=,则AC= 10cm .
【分析】先利用等角的余角相等证明∠B=∠CAD,然后在Rt△ACD中利用∠CAD的余弦求AC的长.
【解答】解:∵AD为高,
∴∠ADB=90°,
∴∠B+∠DAB=90°,
∵∠CAD+∠DAB=90°,
∴∠B=∠CAD,
∴cos∠CAD=cosB=,
在Rt△ACD中,∵cos∠CAD=,
∴AC==10(cm).
故答案为10cm.
15.如图,AB∥CD,AD、BC相交于点E,过E作EF∥CD交BD于点F,如果AB:CD=2:3,EF=6,那么CD的长等于 15 .
【分析】由△ABE∽△DCE,推出==,可得=,再证明△BEF∽△BCD,可得==,由此即可解决问题.
【解答】解:∵AB∥CD,
∴△ABE∽△DCE,
∴==,
∴=,
∵EF∥CD,
∴△BEF∽△BCD,
∴==,
∵EF=6,
∴CD=15,
故答案为15.
16.如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tanD= 2 .
【分析】连接BC可得RT△ACB,由勾股定理求得BC的长,进而由tanD=tanA=可得答案.
【解答】解:如图,连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=6,AC=2,
∴BC===4,
又∵∠D=∠A,
∴tanD=tanA===2.
故答案为:2.
17.一条船从海岛A出发,以15海里/时的速度向正北航行,2小时后到达海岛B处.灯塔C在海岛A的北偏西42°方向上,在海岛B的北偏西84°方向上.则海岛B到灯塔C的距离是 30海里 .
【分析】根据三角形的外角性质求出∠C,进而得到∠C=∠CAB,根据等腰三角形的判定定理得到BC=AB,根据题意计算,得到答案.
【解答】解:根据题意得:∠CBD=84°,∠CAB=42°,
∴∠C=∠CBD﹣∠CAB=42°,
∴∠C=∠CAB,
∴BC=AB,
∵AB=15×2=30(海里),
∴BC=30(海里),
即海岛B到灯塔C的距离是30海里,
故答案为:30海里.
18.如图,Rt△ABC中,∠ACB=90°,AC=BC,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的点A'处,若AO=OB=2,则图中阴影部分面积为 .
【分析】根据等腰直角三角形的性质求出AB,再根据旋转的性质可得A′B=AB,然后求出∠OA′B=30°,再根据直角三角形两锐角互余求出∠A′BA=60°,即旋转角为60°,再根据S阴影=S扇形ABA′+S△A′BC′﹣S△ABC﹣S扇形CBC′=S扇形ABA′﹣S扇形CBC′,然后利用扇形的面积公式列式计算即可得解.
【解答】解:∵∠ACB=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴AB=2OA=2OB=4,BC=2,
∵△ABC绕点B顺时针旋转点A在A′处,
∴BA′=AB,
∴BA′=2OB,
∴∠OA′B=30°,
∴∠A′BA=60°,
即旋转角为60°,
S阴影=S扇形ABA′+S△A′BC′﹣S△ABC﹣S扇形CBC′
=S扇形ABA′﹣S扇形CBC′
=
=.
故答案为:.
三.解答题
19.(1)计算:tan60°+9tan30°﹣8sin60°+2cos45°;
(2)在△ABC中,∠C=90°,AC=,BC=,求∠A的度数.
【分析】(1)代入特殊锐角的三角函数值进行计算即可;
(2)由锐角三角函数定义的定义得tanA==,即可得出答案.
【解答】解:(1)tan60°+9tan30°﹣8sin60°+2cos45°
=+9×﹣8×+2×
=+3﹣4+
=;
(2)∵∠C=90°,AC=,BC=,
∴tanA===,
∴∠A=60°.
20.已知.在△ABC中,BC=AC,∠BCA=135°,求tanA的值.
【分析】过B点作BD⊥AC交AC的延长线于D点,根据等腰直角三角形的性质得到BD=CD=BC,根据正切的定义计算即可.
【解答】解:过B点作BD⊥AC交AC的延长线于D点,
则∠BCD=45,
∴BD=CD=BC,
设AC=k,则BD=CD=k,AD=2k,
tanA==.
21.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
【分析】(1)根据四边形ABCD为平行四边形,利用平行四边形的对边平行且相等,得到一对同旁内角互补,一对内错角相等,根据已知角相等,利用等角的补角相等得到两组对应角相等,从而推知:△ADF∽△DEC;
(2)由△ADF∽△DEC,得比例,求出DE的长.利用勾股定理求出AE的长.
【解答】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
∴△ADF∽△DEC.
(2)解:∵四边形ABCD是平行四边形,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴=,
∴DE===12.
在Rt△ADE中,由勾股定理得:AE==6.
22.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°
(1)判断△ABC的形状,并证明你的结论;
(2)若BC的长为6,求⊙O的半径.
【分析】(1)根据圆周角定理得到∠ABC=∠APC=60°,∠CAB=∠CPB=60°,根据等边三角形的判定定理证明;
(2)延长BO交⊙O于E,连接CE,根据圆周角定理得到∠E=∠BAC=60°,根据正弦的概念计算即可.
【解答】解:(1)△ABC是等边三角形,
理由如下:由圆周角定理得,∠ABC=∠APC=60°,∠CAB=∠CPB=60°,
∴△ABC是等边三角形;
(2)延长BO交⊙O于E,连接CE,
由圆周角定理得,∠E=∠BAC=60°,
∴BE==4,
∴⊙O的半径为2.
23.如图,防洪大堤的横截面ABGH是梯形,背水坡AB的坡度i=1:(垂直高度AE与水平宽度BE的比),AB=20米,BC=30米,身高为1.7米的小明(AM=1.7米)站在大堤A点(M,A,E三点在同一条直线上),测得电线杆顶端D的仰角∠α=20°.
(1)求∠ABC;
(2)求电线杆CD的高度.(结果精确到个位,参考数据sin20°≈0.3,cos20°≈0.9,tan20°≈0.4,≈1.7)
【分析】(1)由tan∠ABE=i=1:,得出∠ABE=30°,即可得出结果;
(2)过M点作MN垂直于CD的于点N,含30°角直角三角形的性质得出AE=AB=10,由三角函数定义得出BE=ABcos30°=10,则CN=AE+AM=11.7,MN=CB+BE=30+10,求出DN=MNtan20°=12+4,即可得出结果.
【解答】解:(1)∵i=1:,
∴tan∠ABE=i=1:,
∴∠ABE=30°,
∴∠ABC=150°;
(2)过M点作MN垂直于CD的于点N,如图所示:
∵AB=20m,∠ABE=30°,
∴AE=AB=×20=10,
BE=ABcos30°=20×=10,
∴CN=AE+AM=10+1.7=11.7,
MN=CB+BE=30+10,
∵∠NMD=20°,MN=30+10,
∴DN=MNtan20°=(30+10)×0.4=12+4,
∴CD=CN+DN=11.7+12+4=23.7+4≈31.
答:电线杆CD的高度约为31米.
24.从三角形(不是等腰三角形)一个顶点引起一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,∠A=48°,CD是△ABC的完美分割线,且AD=CD,求∠ACB的度数.
(2)如图2,在△ABC中,AC=2,BC=,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,找出CD与BD的关系.
【分析】(1)根据相似三角形的性质得到∠BCD=∠A=48°,再根据角的和差关系求出∠ACB即可.
(2)利用△BCD∽△BAC,得=,可得结论.
【解答】解:(1)当AD=CD时,如图3,∠ACD=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=96°.
(2)结论:CD=BD.
∵△BCD∽△BAC,
∵△BCD∽△BAC,
∴=,
∴==,
∴CD=BD.
25.如图,AB是⊙O的直径,点C是⊙O上一点(与点A,B不重合),过点C作直线PQ,使得∠ACQ=∠ABC.
(1)求证:直线PQ是⊙O的切线.
(2)过点A作AD⊥PQ于点D,交⊙O于点E,若⊙O的半径为2,sin∠DAC=,求图中阴影部分的面积.
【分析】(1)连接OC,由直径所对的圆周角为直角,可得∠ACB=90°;利用等腰三角形的性质及已知条件∠ACQ=∠ABC,可求得∠OCQ=90°,按照切线的判定定理可得结论.
(2)由sin∠DAC=,可得∠DAC=30°,从而可得∠ACD的 度数,进而判定△AEO为等边三角形,则∠AOE的度数可得;利用S阴影=S扇形﹣S△AEO,可求得答案.
【解答】解:(1)证明:如图,连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵OA=OC,
∴∠CAB=∠ACO.
∵∠ACQ=∠ABC,
∴∠CAB+∠ABC=∠ACO+∠ACQ=∠OCQ=90°,即OC⊥PQ,
∴直线PQ是⊙O的切线.
(2)连接OE,
∵sin∠DAC=,AD⊥PQ,
∴∠DAC=30°,∠ACD=60°.
∴∠ABC=∠ACD=60°,
∴∠CAB=90°﹣60°=30°,
∴∠EAO=∠DAC+∠CAB=60°,
又∵OA=OE,
∴△AEO为等边三角形,
∴∠AOE=60°.
∴S阴影=S扇形﹣S△AEO
=S扇形﹣OA?OE?sin60°
=×22﹣×2×2×
=﹣.
∴图中阴影部分的面积为﹣.
26.如图,在△ABC中,AM与BN相交于D,BM=3MC,AD=DM,求:
(1)BD:DN的值;
(2)面积S△ABN:S△CBN的值.
【分析】(1)过C作CE∥AM交BA延长线于点E,延长BN交CE于点F,根据相似三角形的性质和平行线分线段成比例定理计算;
(2)根据两三角形高相等,则底边的比等于面积比计算.
【解答】解:(1)过C作CE∥AM交BA延长线于点E,延长BN交CE于点F.
∵CE∥AM,
∴∠DAN=∠FCN,∠ADN=∠CFN,
∴△DAN∽△FCN,
∴=,
又∵AD=DM,
∴=,
∵CE∥AM,
∴===,
∴=,
∴BD:DN=3:=7:1.
(2)由(1)得:△DAN相似于△FCN,
∴==
∴S△ABN:S△CBN=AN:CN=3:4.
同课章节目录
