上海市华二附中2020-2021学年高一上学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 上海市华二附中2020-2021学年高一上学期期末考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 507.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 15:30:47 | ||
图片预览




文档简介
1112520011582400华二附中2020-2021学年高一上期末数学试卷
一、填空题(本大题共10题,每题4分,满分40分)
1.计算:false_________.
2.已知false则false_________.
3.不等式false的解集为_________.
已知扇形的圆心角为false,弧长是false则扇形的面积是_________false.
5.已知幂函数false的图像过点false,则false_________.
6.已知函数false是其反函数,则false_________.
7.方程false的解为:_________.
8.关于false的方程false由实数根,则实数false的取值范围_________.
9.已知false,且false,式子false的最小值是_________.
10.已知函数false,且函数
false为奇函数,则false 的最小值为
二、选择题(本大题共4小题,每题4分,每题16分)
11.已知false是false上的偶函数,false,则“false”是“false”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
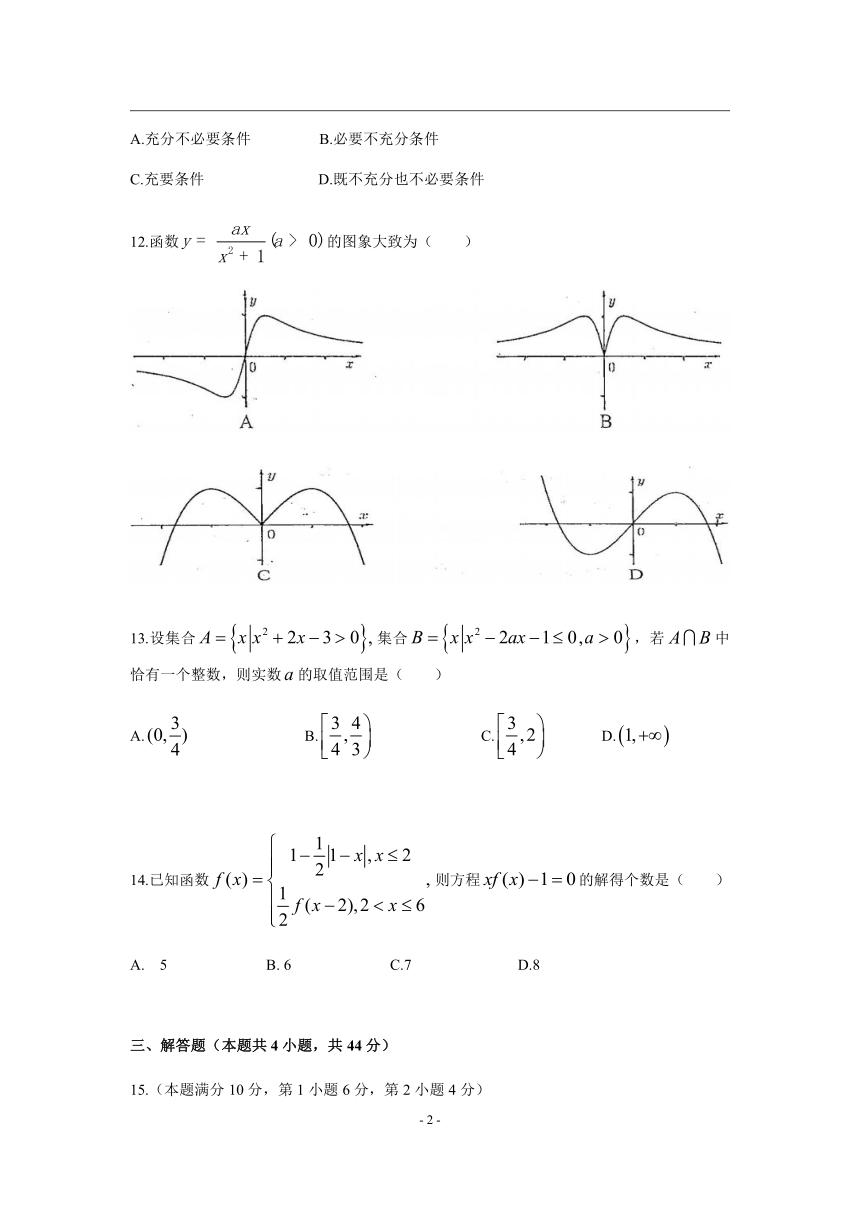
12.函数false的图象大致为( )
13.设集合false集合false,若false中恰有一个整数,则实数false的取值范围是( )
A.false B.false C.false D.false
14.已知函数false则方程false的解得个数是( )
A. 5 B. 6 C.7 D.8
解答题(本题共4小题,共44分)
15.(本题满分10分,第1小题6分,第2小题4分)
已知函数false为奇函数.
(1)求实数a的值并证明false是严格增函数;
(2)若实数满足不等式false,求t的取值范围.
(本大题满分10分,第1小题5分,第2小题5分)
已知函数false.
(1)若函数false的值域为false,求实数false的取值范围;
(2)若函数false在区间false上严格增,求实数false的取值范围。
(本大题满分12分,第1小题4分,第2小题4分,第3小题4分)
新冠肺炎疫情造成医用防护服短缺,某地政府决定为防护服生产企业false公司提供false(万元)的专项补贴, 并以每套80元的价格收购其生产的全部防护服false公司在收到政府false(万元)补贴后, 防护服产量将墙加到false(万件),其中false为工厂工人的复工率false,false公司生产false万件防护服需投入成本false(万元).
(1)将false公司生产防护服的利润 false(万元)表示为补贴false(万元)的函数(利润false总收入一成本,政府补贴false万元计入公司收入中);
(2)在复工率为false时,政府补贴多少万元才能使false公司的防护服利润达到最大?
(3)对任意的false (万元),当复工案false达到多少时,false公司才能不产生亏损? (精确
0.01)
(本大题满分12分,第1小题4分,第2小题4分,第3小题4分)
已知函数false,false.
(1)当false时,求函数false的值域;
(2)若关于false的方程false有两个不等根false,求false的值;
(3)已知存在实数false,使得对任意false,关于false的方程
false在区间false上总有false个不等根false,false,false,求出实数false的取值范围.
1112520011582400华二附中2020-2021学年高一上期末数学试卷(答案)
一、填空题(本大题共10题,每题4分,满分40分)
1.计算:false_________.
【解析】false
2.已知false则false_________.
【解析】false
3.不等式false的解集为_________.
【解析】false
已知扇形的圆心角为false,弧长是false则扇形的面积是_________false.
【解析】false
5.已知幂函数false的图像过点false,则false_________.
【解析】false
6.已知函数false是其反函数,则false_________.
【解析】令false,false
7.方程false的解为:_________.
【解析】false
8.关于false的方程false由实数根,则实数false的取值范围_________.
【解析】由false得false有解,所以false
9.已知false,且false,式子false的最小值是_________.
【解析】false
所以false
false
10.已知函数false,且函数
false为奇函数,则false 的最小值为
【解析】false
false,
false,
所以false,所以false,
所以false,
当false时取得最小值false.
二、选择题(本大题共4小题,每题4分,每题16分)
11.已知false是false上的偶函数,false,则“false”是“false”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【解析】由定义知,前可以推后;反之当false为常值函数时,后不能推前,因此选A
12.函数false的图象大致为( )
【解析】A
13.设集合false集合false,若false中恰有一个整数,则实数false的取值范围是( )
A.false B.false C.false D.false
【解析】false,
函数false得对称轴为false,
而且false
故函数较小的零点在false之间,另一个零点大于1,
要使得false中恰有一个整数,则这个整数解只能为2
所以false解得false,故选B
14.已知函数false则方程false的解得个数是( )
A. 5 B. 6 C.7 D.8
【解析】在同一坐标系作出false与false得图像知,函数得零点个数为7.
解答题(本题共4小题,共44分)
15.(本题满分10分,第1小题6分,第2小题4分)
已知函数false为奇函数.
(1)求实数a的值并证明false是严格增函数;
(2)若实数满足不等式false,求t的取值范围.
【解析】(1)因为false是定义域为R奇函数,
由定义false,所以false
所以false, ∴false. 所以false
证明:任取false,
false.
false,false.
false,即false.
false在定义域上为严格增函数.
(2)由(1)得false是定义域为R奇函数和严格增函数
false
falsefalsefalsefalse
所以false
(本大题满分10分,第1小题5分,第2小题5分)
已知函数false.
(1)若函数false的值域为false,求实数false的取值范围;
(2)若函数false在区间false上严格增,求实数false的取值范围。
【解析】(1)当false时,false满足题意;
当false时,要使得false的值域为false,
只需要满足false,解得false,综上false
false
当false时,外层函数为严格增,所以只需满足false;
当false时,外层函数为严格减,所以只需满足false,此时不存在,舍去;
综上false.
(本大题满分12分,第1小题4分,第2小题4分,第3小题4分)
新冠肺炎疫情造成医用防护服短缺,某地政府决定为防护服生产企业false公司提供false(万元)的专项补贴, 并以每套80元的价格收购其生产的全部防护服false公司在收到政府false(万元)补贴后, 防护服产量将墙加到false(万件),其中false为工厂工人的复工率false,false公司生产false万件防护服需投入成本false(万元).
(1)将false公司生产防护服的利润 false(万元)表示为补贴false(万元)的函数(利润false总收入一成本,政府补贴false万元计入公司收入中);
(2)在复工率为false时,政府补贴多少万元才能使false公司的防护服利润达到最大?
(3)对任意的false (万元),当复工案false达到多少时,false公司才能不产生亏损? (精确
0.01)
【解析】(1)false
false
false
因为false,所以false,
所以false,
当且仅当false,即false时,等号成立.
所以false,
故政府补贴为false万元才能使A公司的防护服利润达到最大,最大为false万元
(3)若对任意的false,公司都不产生亏损,
则false在false恒成立,
即false,记false,则false,
此时false,
由于函数false在false单调递增,
所以当false时,false,
所以false,
即当工厂工人的复工率到false时,对任意的false,公司都不产生亏损。
(本大题满分12分,第1小题4分,第2小题4分,第3小题4分)
已知函数false,false.
(1)当false时,求函数false的值域;
(2)若关于false的方程false有两个不等根false,求false的值;
(3)已知存在实数false,使得对任意false,关于false的方程
false在区间false上总有false个不等根false,false,false,求出实数false的取值范围.
【解析】(1)false在区间false上严格减,
而false,false,故函数false的值域为false.
(2)因为false在false单调递减,在false单调递增,
false false,则有false,即false
故false,所以false
(3)令false,由(1)知false
令false,因为false在false单调减,在false单调递增,
且false,false,false
则当false时,方程false有两个不等根,由(2)知,且两根之积为1;
当false时,方程false有且只有一个根且此根在区间false内或者为1.
令false,由二次函数false与false的图象特征,原题目等价于:
对任意false,关于false的方程false在区间false上总有2个不等根false,
且false有两个不等根,false只有一个根,则必有false
结合二次函数false的图象,则有false,解之得false,
一、填空题(本大题共10题,每题4分,满分40分)
1.计算:false_________.
2.已知false则false_________.
3.不等式false的解集为_________.
已知扇形的圆心角为false,弧长是false则扇形的面积是_________false.
5.已知幂函数false的图像过点false,则false_________.
6.已知函数false是其反函数,则false_________.
7.方程false的解为:_________.
8.关于false的方程false由实数根,则实数false的取值范围_________.
9.已知false,且false,式子false的最小值是_________.
10.已知函数false,且函数
false为奇函数,则false 的最小值为
二、选择题(本大题共4小题,每题4分,每题16分)
11.已知false是false上的偶函数,false,则“false”是“false”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
12.函数false的图象大致为( )
13.设集合false集合false,若false中恰有一个整数,则实数false的取值范围是( )
A.false B.false C.false D.false
14.已知函数false则方程false的解得个数是( )
A. 5 B. 6 C.7 D.8
解答题(本题共4小题,共44分)
15.(本题满分10分,第1小题6分,第2小题4分)
已知函数false为奇函数.
(1)求实数a的值并证明false是严格增函数;
(2)若实数满足不等式false,求t的取值范围.
(本大题满分10分,第1小题5分,第2小题5分)
已知函数false.
(1)若函数false的值域为false,求实数false的取值范围;
(2)若函数false在区间false上严格增,求实数false的取值范围。
(本大题满分12分,第1小题4分,第2小题4分,第3小题4分)
新冠肺炎疫情造成医用防护服短缺,某地政府决定为防护服生产企业false公司提供false(万元)的专项补贴, 并以每套80元的价格收购其生产的全部防护服false公司在收到政府false(万元)补贴后, 防护服产量将墙加到false(万件),其中false为工厂工人的复工率false,false公司生产false万件防护服需投入成本false(万元).
(1)将false公司生产防护服的利润 false(万元)表示为补贴false(万元)的函数(利润false总收入一成本,政府补贴false万元计入公司收入中);
(2)在复工率为false时,政府补贴多少万元才能使false公司的防护服利润达到最大?
(3)对任意的false (万元),当复工案false达到多少时,false公司才能不产生亏损? (精确
0.01)
(本大题满分12分,第1小题4分,第2小题4分,第3小题4分)
已知函数false,false.
(1)当false时,求函数false的值域;
(2)若关于false的方程false有两个不等根false,求false的值;
(3)已知存在实数false,使得对任意false,关于false的方程
false在区间false上总有false个不等根false,false,false,求出实数false的取值范围.
1112520011582400华二附中2020-2021学年高一上期末数学试卷(答案)
一、填空题(本大题共10题,每题4分,满分40分)
1.计算:false_________.
【解析】false
2.已知false则false_________.
【解析】false
3.不等式false的解集为_________.
【解析】false
已知扇形的圆心角为false,弧长是false则扇形的面积是_________false.
【解析】false
5.已知幂函数false的图像过点false,则false_________.
【解析】false
6.已知函数false是其反函数,则false_________.
【解析】令false,false
7.方程false的解为:_________.
【解析】false
8.关于false的方程false由实数根,则实数false的取值范围_________.
【解析】由false得false有解,所以false
9.已知false,且false,式子false的最小值是_________.
【解析】false
所以false
false
10.已知函数false,且函数
false为奇函数,则false 的最小值为
【解析】false
false,
false,
所以false,所以false,
所以false,
当false时取得最小值false.
二、选择题(本大题共4小题,每题4分,每题16分)
11.已知false是false上的偶函数,false,则“false”是“false”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【解析】由定义知,前可以推后;反之当false为常值函数时,后不能推前,因此选A
12.函数false的图象大致为( )
【解析】A
13.设集合false集合false,若false中恰有一个整数,则实数false的取值范围是( )
A.false B.false C.false D.false
【解析】false,
函数false得对称轴为false,
而且false
故函数较小的零点在false之间,另一个零点大于1,
要使得false中恰有一个整数,则这个整数解只能为2
所以false解得false,故选B
14.已知函数false则方程false的解得个数是( )
A. 5 B. 6 C.7 D.8
【解析】在同一坐标系作出false与false得图像知,函数得零点个数为7.
解答题(本题共4小题,共44分)
15.(本题满分10分,第1小题6分,第2小题4分)
已知函数false为奇函数.
(1)求实数a的值并证明false是严格增函数;
(2)若实数满足不等式false,求t的取值范围.
【解析】(1)因为false是定义域为R奇函数,
由定义false,所以false
所以false, ∴false. 所以false
证明:任取false,
false.
false,false.
false,即false.
false在定义域上为严格增函数.
(2)由(1)得false是定义域为R奇函数和严格增函数
false
falsefalsefalsefalse
所以false
(本大题满分10分,第1小题5分,第2小题5分)
已知函数false.
(1)若函数false的值域为false,求实数false的取值范围;
(2)若函数false在区间false上严格增,求实数false的取值范围。
【解析】(1)当false时,false满足题意;
当false时,要使得false的值域为false,
只需要满足false,解得false,综上false
false
当false时,外层函数为严格增,所以只需满足false;
当false时,外层函数为严格减,所以只需满足false,此时不存在,舍去;
综上false.
(本大题满分12分,第1小题4分,第2小题4分,第3小题4分)
新冠肺炎疫情造成医用防护服短缺,某地政府决定为防护服生产企业false公司提供false(万元)的专项补贴, 并以每套80元的价格收购其生产的全部防护服false公司在收到政府false(万元)补贴后, 防护服产量将墙加到false(万件),其中false为工厂工人的复工率false,false公司生产false万件防护服需投入成本false(万元).
(1)将false公司生产防护服的利润 false(万元)表示为补贴false(万元)的函数(利润false总收入一成本,政府补贴false万元计入公司收入中);
(2)在复工率为false时,政府补贴多少万元才能使false公司的防护服利润达到最大?
(3)对任意的false (万元),当复工案false达到多少时,false公司才能不产生亏损? (精确
0.01)
【解析】(1)false
false
false
因为false,所以false,
所以false,
当且仅当false,即false时,等号成立.
所以false,
故政府补贴为false万元才能使A公司的防护服利润达到最大,最大为false万元
(3)若对任意的false,公司都不产生亏损,
则false在false恒成立,
即false,记false,则false,
此时false,
由于函数false在false单调递增,
所以当false时,false,
所以false,
即当工厂工人的复工率到false时,对任意的false,公司都不产生亏损。
(本大题满分12分,第1小题4分,第2小题4分,第3小题4分)
已知函数false,false.
(1)当false时,求函数false的值域;
(2)若关于false的方程false有两个不等根false,求false的值;
(3)已知存在实数false,使得对任意false,关于false的方程
false在区间false上总有false个不等根false,false,false,求出实数false的取值范围.
【解析】(1)false在区间false上严格减,
而false,false,故函数false的值域为false.
(2)因为false在false单调递减,在false单调递增,
false false,则有false,即false
故false,所以false
(3)令false,由(1)知false
令false,因为false在false单调减,在false单调递增,
且false,false,false
则当false时,方程false有两个不等根,由(2)知,且两根之积为1;
当false时,方程false有且只有一个根且此根在区间false内或者为1.
令false,由二次函数false与false的图象特征,原题目等价于:
对任意false,关于false的方程false在区间false上总有2个不等根false,
且false有两个不等根,false只有一个根,则必有false
结合二次函数false的图象,则有false,解之得false,
同课章节目录
