2020-2021学年七年数学级人教版下册5.1.3同位角、内错角、同旁内角课件(16张)
文档属性
| 名称 | 2020-2021学年七年数学级人教版下册5.1.3同位角、内错角、同旁内角课件(16张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 574.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 00:00:00 | ||
图片预览



文档简介
5.1.2 垂线
R·七年级下册
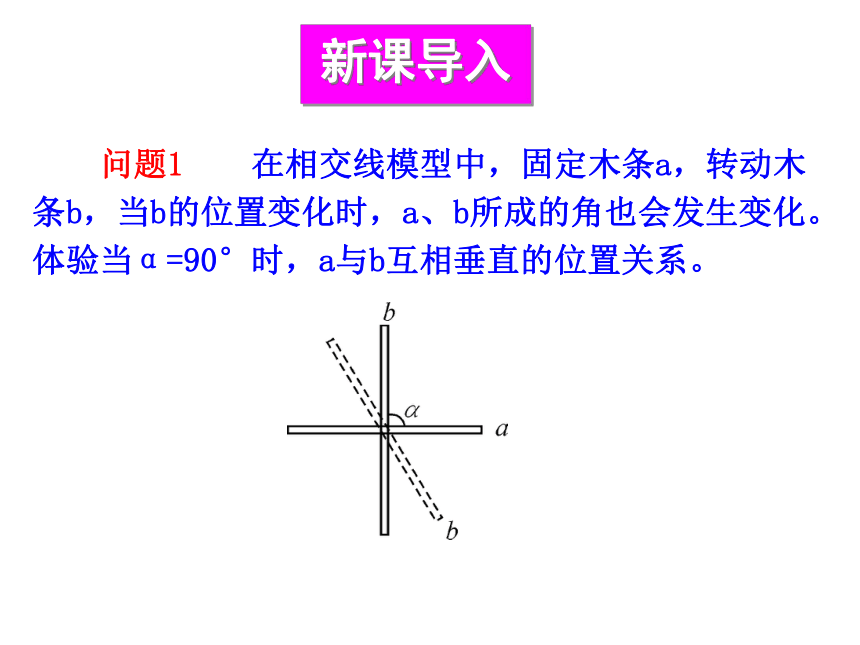
问题1 在相交线模型中,固定木条a,转动木条b,当b的位置变化时,a、b所成的角也会发生变化。体验当α=90°时,a与b互相垂直的位置关系。
新课导入
自学交流
什么是垂直?什么是垂线?什么是垂足?
思考 1.两条直线相交,所成的4个角中。如果有一个角是90°,那么其余各角分别是多少度?
定义:两条直线相交所形成的四个角中,如果有一个角是90°,那么这两条直线互相垂直。其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
∟
其余各角都是90°
获取新知
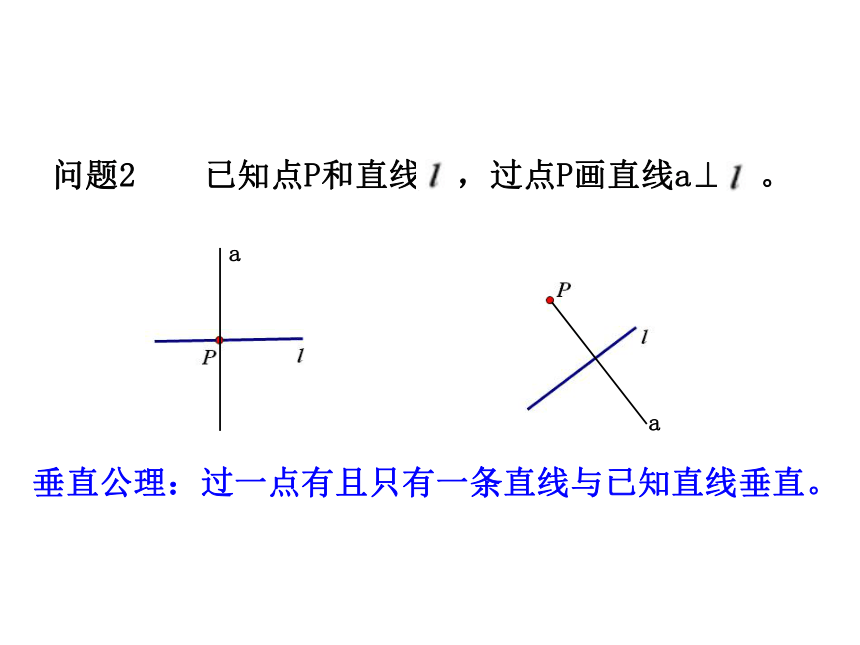
问题2 已知点P和直线 ,过点P画直线a⊥ 。
a
a
垂直公理:过一点有且只有一条直线与已知直线垂直。
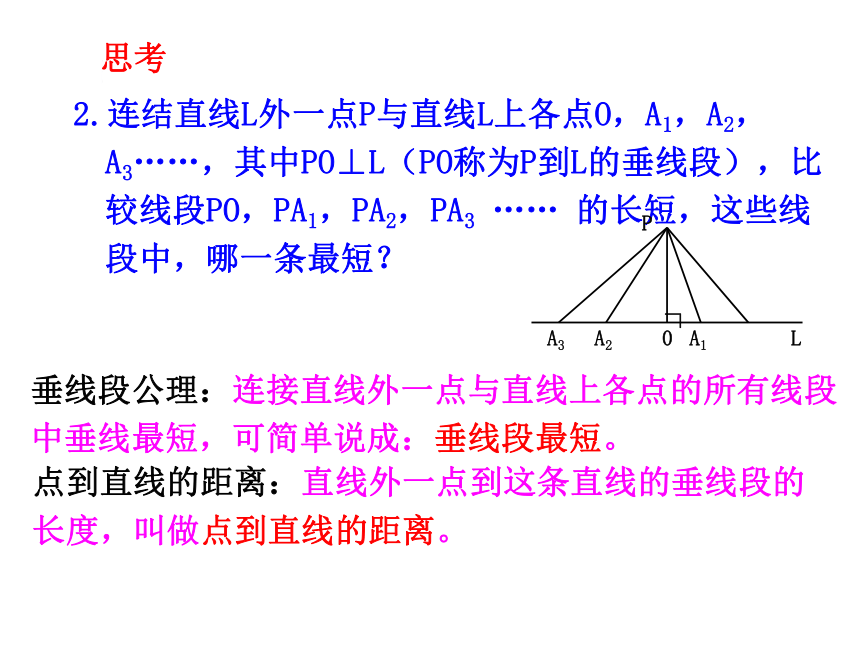
2.连结直线L外一点P与直线L上各点O,A1,A2,A3……,其中PO⊥L(PO称为P到L的垂线段),比较线段PO,PA1,PA2,PA3 …… 的长短,这些线段中,哪一条最短?
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
垂线段公理:连接直线外一点与直线上各点的所有线段中垂线最短,可简单说成:垂线段最短。
∟
A1
A2
A3
0
P
L
思考
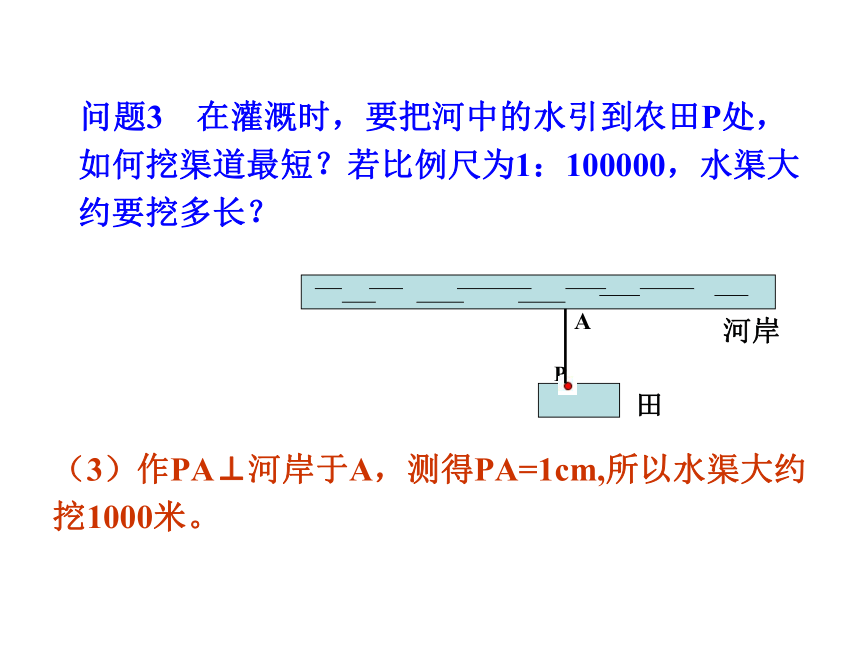
问题3 在灌溉时,要把河中的水引到农田P处,如何挖渠道最短?若比例尺为1:100000,水渠大约要挖多长?
P
田
河岸
A
(3)作PA⊥河岸于A,测得PA=1cm,所以水渠大约挖1000米。
练一练
3、垂线段和点到直线的距离的区别与联系:
区 别
联 系
垂线段是图形,点到直线的距离是一个长度,是一个数量,不是垂线段这个图形本身
点到直线的距离是相对应的垂线段的长度,没有作出这条垂线段,就无法度量出点到直线的距离
如图,三角形ABC中,∠C=90°.
(1)分别指出点A到直线BC,点B到直线AC的距离是哪些线段的长;
(2)三条边AB,AC,BC中哪条边最长?为什么?
A
B
C
练一练
1、如图,CO⊥AB于O,OD⊥OE,∠AOE=42°,求∠DOC的度数。
解:CO⊥AB于O,OD⊥OE,
由垂直的定义可得∠AOC=90°,∠DOE=90°。
则∠COE=∠AOC-∠AOE=90°-42°=48°,∠DOC=∠DOE-∠COE=90°-48°=42°
A
B
C
D
E
O
运用新知
2.小刚牵着一头小羊从A先到B拿东西,再到河边让小牛饮水,请画出小刚的最佳行走路线,并说明这种画法的理由。
解:小刚的最佳行走路线如图,理由:两点间的线段最短;点到直线的垂线段最短。
∟
A
B
3、如图,PR⊥L,QR⊥L,R为垂足,那么P,Q,R在同一直线上吗?
解:P、Q、R在同一直线上,过一点有且只有一条直线与已知直线垂直。
L
∟
P
Q
R
·
·
·
4、如图,已知AOB为一条直线,OC为一条射线,OD平分∠BOC,OE平分∠AOC,试判断OD与OE的位置关系,并说明理由。
A
B
C
D
E
O
解:OD⊥OE,理由如下:AOB为一条直线,∠AOB=180°,OD平分∠BOC,OE平分∠AOC,
所以∠DOC= ∠BOC,∠EOC= ∠AOC,
所以∠DOE=∠DOC+∠EOC= (∠BOC+∠AOC)=
∠AOB=90 °,即OD⊥OE。
垂直定义,点到直线的距离,
垂直公理,垂线段公理。
课堂小结
R·七年级下册
问题1 在相交线模型中,固定木条a,转动木条b,当b的位置变化时,a、b所成的角也会发生变化。体验当α=90°时,a与b互相垂直的位置关系。
新课导入
自学交流
什么是垂直?什么是垂线?什么是垂足?
思考 1.两条直线相交,所成的4个角中。如果有一个角是90°,那么其余各角分别是多少度?
定义:两条直线相交所形成的四个角中,如果有一个角是90°,那么这两条直线互相垂直。其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
∟
其余各角都是90°
获取新知
问题2 已知点P和直线 ,过点P画直线a⊥ 。
a
a
垂直公理:过一点有且只有一条直线与已知直线垂直。
2.连结直线L外一点P与直线L上各点O,A1,A2,A3……,其中PO⊥L(PO称为P到L的垂线段),比较线段PO,PA1,PA2,PA3 …… 的长短,这些线段中,哪一条最短?
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
垂线段公理:连接直线外一点与直线上各点的所有线段中垂线最短,可简单说成:垂线段最短。
∟
A1
A2
A3
0
P
L
思考
问题3 在灌溉时,要把河中的水引到农田P处,如何挖渠道最短?若比例尺为1:100000,水渠大约要挖多长?
P
田
河岸
A
(3)作PA⊥河岸于A,测得PA=1cm,所以水渠大约挖1000米。
练一练
3、垂线段和点到直线的距离的区别与联系:
区 别
联 系
垂线段是图形,点到直线的距离是一个长度,是一个数量,不是垂线段这个图形本身
点到直线的距离是相对应的垂线段的长度,没有作出这条垂线段,就无法度量出点到直线的距离
如图,三角形ABC中,∠C=90°.
(1)分别指出点A到直线BC,点B到直线AC的距离是哪些线段的长;
(2)三条边AB,AC,BC中哪条边最长?为什么?
A
B
C
练一练
1、如图,CO⊥AB于O,OD⊥OE,∠AOE=42°,求∠DOC的度数。
解:CO⊥AB于O,OD⊥OE,
由垂直的定义可得∠AOC=90°,∠DOE=90°。
则∠COE=∠AOC-∠AOE=90°-42°=48°,∠DOC=∠DOE-∠COE=90°-48°=42°
A
B
C
D
E
O
运用新知
2.小刚牵着一头小羊从A先到B拿东西,再到河边让小牛饮水,请画出小刚的最佳行走路线,并说明这种画法的理由。
解:小刚的最佳行走路线如图,理由:两点间的线段最短;点到直线的垂线段最短。
∟
A
B
3、如图,PR⊥L,QR⊥L,R为垂足,那么P,Q,R在同一直线上吗?
解:P、Q、R在同一直线上,过一点有且只有一条直线与已知直线垂直。
L
∟
P
Q
R
·
·
·
4、如图,已知AOB为一条直线,OC为一条射线,OD平分∠BOC,OE平分∠AOC,试判断OD与OE的位置关系,并说明理由。
A
B
C
D
E
O
解:OD⊥OE,理由如下:AOB为一条直线,∠AOB=180°,OD平分∠BOC,OE平分∠AOC,
所以∠DOC= ∠BOC,∠EOC= ∠AOC,
所以∠DOE=∠DOC+∠EOC= (∠BOC+∠AOC)=
∠AOB=90 °,即OD⊥OE。
垂直定义,点到直线的距离,
垂直公理,垂线段公理。
课堂小结
