2.1 两条直线的位置关系(2)垂线同步练习(含解析)
文档属性
| 名称 | 2.1 两条直线的位置关系(2)垂线同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 13:08:57 | ||
图片预览




文档简介
2.2两条直线的位置关系(2)垂线
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020?陕西)如图,AC⊥BC,直线EF经过点C,若∠1=35°,则∠2的大小为( )
A.65° B.55° C.45° D.35°
2.(2020春?丛台区校级月考)如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.两点之间,线段最短
3.(2020春?高州市期中)如图,直线AB⊥CD于O,直线EF交AB于O,∠COF=70°,则∠AOE等于( )
A.20° B.30° C.35° D.70°
4.(2020春?文水县期末)如图,直线AB,CD相交于点O,下列条件中能说明AB⊥CD的有( )
①∠AOD=90°;
②∠AOD=∠AOC;
③∠AOC+∠BOC=180°;
④∠AOC+∠BOD=180°.
A.1个 B.2个 C.3个 D.4个
5.(2020春?抚顺县期末)O为直线AB上一点,OC⊥OD,若∠1=40°,则∠2=( )
A.30° B.40° C.50° D.60°
6.(2020?南海区校级模拟)如图,CA⊥AB,EA⊥AD,已知∠DAB=45°,那么∠EAC的大小是( )
A.50° B.45° C.30° D.60°
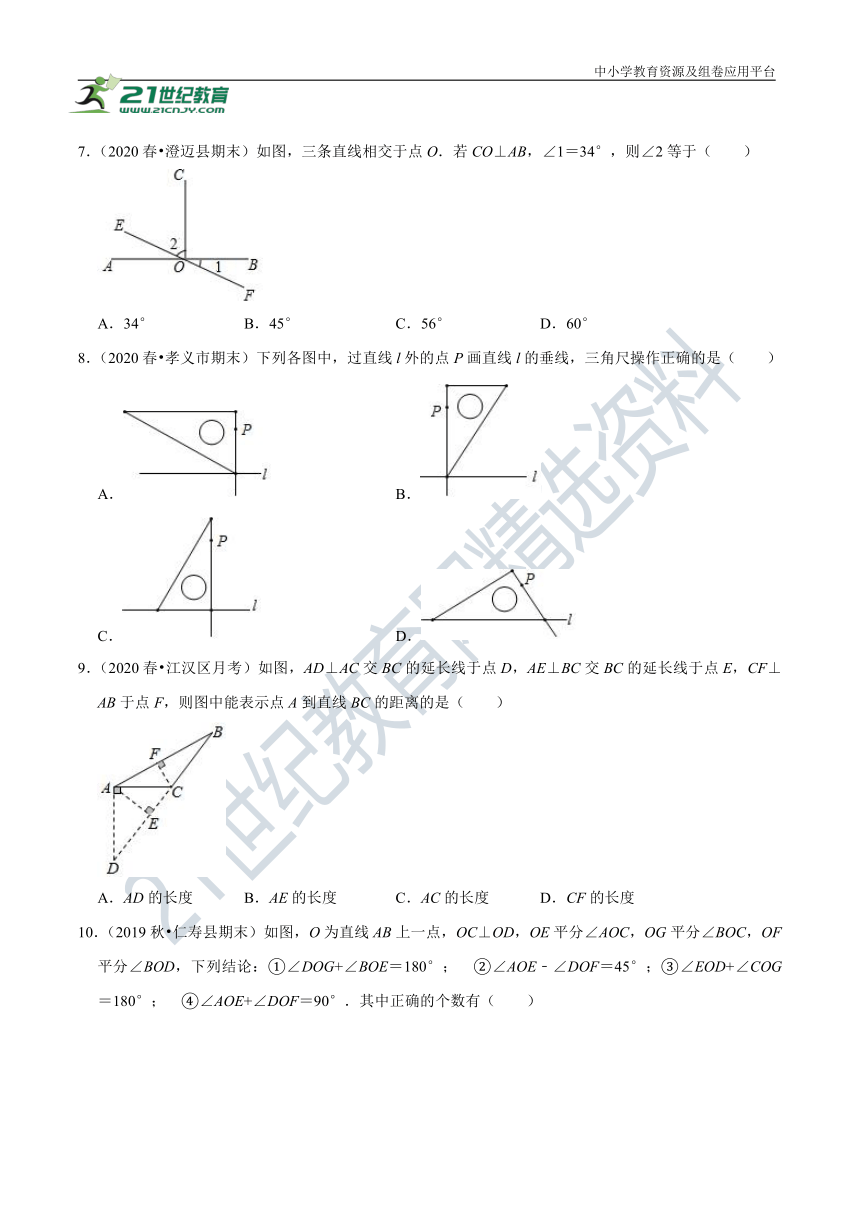
7.(2020春?澄迈县期末)如图,三条直线相交于点O.若CO⊥AB,∠1=34°,则∠2等于( )
A.34° B.45° C.56° D.60°
8.(2020春?孝义市期末)下列各图中,过直线l外的点P画直线l的垂线,三角尺操作正确的是( )
A. B.
C. D.
9.(2020春?江汉区月考)如图,AD⊥AC交BC的延长线于点D,AE⊥BC交BC的延长线于点E,CF⊥AB于点F,则图中能表示点A到直线BC的距离的是( )
A.AD的长度 B.AE的长度 C.AC的长度 D.CF的长度
10.(2019秋?仁寿县期末)如图,O为直线AB上一点,OC⊥OD,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论:①∠DOG+∠BOE=180°; ②∠AOE﹣∠DOF=45°;③∠EOD+∠COG=180°; ④∠AOE+∠DOF=90°.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020秋?肇源县期末)两条直线相交所构成的四个角,其中:①有三个角都相等;②有一对对顶角相等;③有一个角是直角;④有一对邻补角相等,能判定这两条直线垂直的有 .
12.(2020春?黄埔区期末)如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠AOD=118°,则∠EOC的度数为 .
13.(2020秋?香坊区校级期中)如图,直线AB⊥CD,EF经过点O,∠2=2∠1,则∠3= °.
14.(2020秋?南岗区校级期中)已知,∠AOB和∠BOC互为邻补角,且∠BOC:∠AOB=4:1,射线OD平分∠AOB,射线OE⊥OD,则∠BOE= .
15.(2020春?太平区期末)关于垂线,小明给出了下面三种说法:①两条直线相交,所构成的四个角中有一个角是直角,那么这两条直线互相垂直;②两条直线的交点叫垂足;③直线AB⊥CD,也可以说成CD⊥AB.其中正确的有 (填序号).
16.(2020春?鱼台县期末)如图,村庄A到公路BC的最短距离是AD的长,其根据是 .
17.(2020春?东城区校级期末)如图,∠C=90°,线段AB=15cm,线段AD=12cm,线段AC=9cm,则点A到BC的距离为 cm.
18.(2020春?岳阳期末)如图,在三角形ABC中,∠ABC=90°,BD⊥AC,垂足为点D,AB=5,BC=12,AC=13,下列结论正确的是 .(写出所有正确结论的序号)
①∠ADB=90°;
②∠A=∠DBC;
③点C到直线BD的距离为线段CB的长度;
④点B到直线AC的距离为6013.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020春?赣州期末)如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
20.(2020秋?长春期末)如图,直线AB与直线MN相交,交点为O,OC⊥AB,OA平分∠MOD,若∠BON=20°,求∠COD的度数.
21.(2019秋?姜堰区期末)如图,直线AB、CD相交于点O,OM⊥AB,∠1=∠2.
(1)求∠NOD的度数;
(2)若∠AOD=3∠1,求∠AOC和∠MOD的度数.
22.(2020秋?香坊区校级期中)如图,直线AB、CD相交于点O,OE平分∠AOC,OF⊥OE于O,且∠DOF=74°,求∠BOD的度数.
23.(2019秋?翠屏区期末)如图,射线OC、OD把∠AOB分成三个角,且度数之比是∠AOC:∠COD:∠DOB=2:3:4,射线OM平分∠AOC,射线ON平分∠BOD,且OM⊥ON.
(1)求∠COD的度数;
(2)求∠AOB的补角的度数.
24.(2019秋?市中区期末)将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图(1),若∠BOD=35°,则∠AOC= ;若∠AOC=135°,则∠BOD= ;(直接写出结论即可)
(2)如图(2),若∠AOC=140°,则∠BOD= ;(直接写出结论即可)
(3)猜想∠AOC与∠BOD的大小关系,并结合图(1)说明理由;
(4)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当锐角∠AOD等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD角度所有可能的值,不用说明理由.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】∵AC⊥BC,
∴∠ACB=90°,
∵∠1+∠ACB+∠2=180°,
∴∠2=180°﹣90°﹣35°=55°,
故选:B.
2.【解析】如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是在同一平面内,过一点有且只有一条直线与已知直线垂直,
故选:C.
3.【解析】∵AB⊥CD,
∴∠COB=90°,
∵∠COF=70°,
∴∠BOF=90°﹣70°=20°,
∴∠AOE=20°,
故选:A.
4.【解析】①∠AOD=90°可以判定两直线垂直,故此选项符合题意;
②∠AOD和∠AOC是邻补角,邻补角相等和又是180°,所以可以得到∠AOC=90°,能判定垂直,故此选项符合题意;
③∠AOC和∠BOC是邻补角,邻补角的和是180°,不能判定垂直,故此选项不符合题意;
④∠AOC和∠BOD是对顶角,对顶角相等,和又是180°,所以可得到∠AOC=90°,故此选项符合题意.
综上所述,①②④共3个正确,
故选:C.
5.【解析】∵OC⊥OD,
∴∠COD=90°,
∴∠1+∠2=90°,
∵∠1=40°,
∴∠2=90°﹣40°=50°,
故选:C.
6.【解析】∵CA⊥AB,
∴∠CAD+∠DAB=∠CAB=90°,
∵∠DAB=45°,
∴∠CAD=45°,
∵EA⊥AD,
∴∠EAD=90°,
∴∠EAC=90°﹣∠CAD=90°﹣45°=45°,
故选:B.
7.【解析】∵CO⊥AB,
∴∠COB=90°,
∵∠1=34°,
∴∠2=180°﹣90°﹣34°=56°,
故选:C.
8.【解析】用直角三角板的一条直角边与l重合,另一条直角边过点P后沿直角边画直线,
∴C选项的画法正确,
故选:C.
9.【解析】图中能表示点A到直线BC的距离的是AE的长度,
故选:B.
10.【解析】∵OE平分∠AOC,OG平分∠BOC,
∴可设∠AOE=∠COE=α,∠BOG=∠COG=β,
∵O为直线AB上一点,
∴∠AOB=180°,
∴2α+2β=180°,
∴α+β=90°,∠EOG=90°.
∵∠DOC=90°,
∴∠DOG=∠COE=90°﹣∠COG=α,
∴∠BOD=∠DOG﹣∠BOG=α﹣β.
∵OF平分∠BOD,
∴∠BOF=∠DOF=12(α﹣β).
①∵∠DOG=α=∠AOE,∠AOE+∠BOE=180°,
∴∠DOG+∠BOE=180°,
故本选项结论正确;
②∵∠AOE=α,∠DOF=12(α﹣β),
∴∠AOE﹣∠DOF=α-12(α﹣β)=12(α+β)=45°,
故本选项结论正确;
③∵∠EOD=∠EOG+∠GOD=90°+α,∠COG=β,
∴∠EOD+∠COG=90°+α+β=180°,
故本选项结论正确;
④∵∠AOE+∠DOF=α+12(α﹣β)=32α-12β=32α-12(90°﹣α)=2α﹣45°,
∴当α=67.5°时,∠AOE+∠DOF=90°,
但是题目没有α=67.5°的条件,
故本选项结论错误.
综上所述,正确的有:①②③共3个.
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】两条直线相交所构成的四个角,
①因为有三个角都相等,都等于90°,所以能判定这两条直线垂直;
②因为有一对对顶角相等,但不一定等于90°,所以不能判定这两条直线垂直;
③有一个角是直角,能判定这两条直线垂直;
④因为一对邻补角相加等于180°,这对邻补角又相等都等于90°,所以能判定这两条直线垂直;
故答案为:①③④.
12.【解析】∵∠AOD=118°,
∴∠BOC=∠AOD=118°,
∵EO⊥AB,
∴∠BOE=90°,
∴∠EOC=∠BOC﹣∠BOE=28°,
故答案为:28°.
13.【解析】∵AB⊥CD,
∴∠1+∠2=90°,
又∵∠2=2∠1,
∴3∠1=90°,
∴∠1=30°,
∴∠3=∠1=30°,
故答案为:30.
14.【解析】∵∠AOB和∠BOC互为邻补角,
∴∠AOB+∠BOC=180°,
又∵∠BOC:∠AOB=4:1,
∴∠BOC=180°×45=144°,∠AOB=180°×15=36°,
∵射线OD平分∠AOB,
∴∠AOD=∠BOD=12∠AOB=18°,
∵OE⊥OD,
∴∠DOE=90°,
如图1,∠BOE=∠DOE﹣∠BOD=90°﹣18°=72°,
如图2,∠BOE=∠DOE+∠BOD=90°+18°=108°,
故答案为:72°或108°.
15.【解析】①两条直线相交,所构成的四个角中有一个角是直角,那么这两条直线互相垂直,故原题说法正确;
②两条直线的交点叫交点,故原题说法错误;
③直线AB⊥CD,也可以说成CD⊥AB,故原题说法正确,
正确的说法有2个,
故答案为:①③.
16.【解析】村庄A到公路BC的最短距离是AD的长,其根据是垂线段最短,
故答案为:垂线段最短.
17.【解析】因为∠C=90°,
所以AC⊥BC,
所以A到BC的距离是AC,
因为线段AC=9cm,
所以点A到BC的距离为9cm.
故答案为:9.
18.【解析】①∵BD⊥AC,
∴∠ADB=90°,故①正确;
②∵∠ABD+∠A=90°,∠ABD+∠DBC=90°,
∴∠A=∠DBC,故②正确;
③点C到直线BD的距离为线段CD的长度,故③错误;
④点B到直线AC的距离为12×5×12×2÷13=6013,故④正确.
故答案为:①②④.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】如图所示
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
20.【解析】∵∠BON=20°,
∴∠AOM=20°,
∵OA平分∠MOD,
∴∠AOD=∠MOA=20°,
∵OC⊥AB,
∴∠AOC=90°,
∴∠COD=90°﹣20°=70°.
21.【解析】证明:(1)∵OM⊥AB,
∴∠AOM=∠BOM=90°,
∴∠1+∠AOC=90°,
∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴∠NOD=180°﹣∠CON=180°﹣90°=90°;
(2)∵∠AOD=3∠1,
∴∠NOD=2∠1=90°,
解得:∠1=45°,
∴∠AOC=∠AOM﹣∠1=90°﹣45°=45°;
∴∠BOD=90°﹣45°=45°,
∴∠MOD=∠BOD+∠BOM=45°+90°=135°.
故答案为:(1)90°; (2)45°,135°.
22.【解析】∵OF⊥OE,
∴∠EOF=90°,
又∵∠COE+∠EOF+∠DOF=180°,∠DOF=74°,
∴∠COE=180°﹣90°﹣74°=16°,
∵OE平分∠AOC,
∴∠AOC=2∠COE=32°=∠BOD,
答:∠BOD的度数为32°.
23.【解析】(1)设∠AOC=2x,∠COD=3x,∠DOB=4x,则∠AOB=9x,
∵OM平分∠AOC,ON平分∠DOB,
∴∠MOC=x,∠NOD=2x,
∴∠MON=x+3x+2x=6x,
又∵OM⊥ON,
∴∠MON=90°,
即6x=90°,
解得x=15°,
∴∠COD=45°;
(2)∵∠AOB=9×15°=135°,
∴∠AOB的补角的度数为45°.
24.【解析】(1)若∠BOD=35°,
∵∠AOB=∠COD=90°,
∴∠AOC=∠AOB+∠COD﹣∠BOD=90°+90°﹣35°=145°,
若∠AOC=135°,
则∠BOD=∠AOB+∠COD﹣∠AOC=90°+90°﹣135°=45°;
故答案为:145°;45°;
(2)如图2,若∠AOC=140°,
则∠BOD=360°﹣∠AOC﹣∠AOB﹣∠COD
=360°﹣140°﹣90°﹣90°
=40°;
故答案为:40°;
(3)∠AOC与∠BOD互补.
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOD+∠BOD+∠BOC=180°.
∵∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180°,
即∠AOC与∠BOD互补.
(4)OD⊥AB时,∠AOD=30°,
CD⊥OB时,∠AOD=45°,
CD⊥AB时,∠AOD=75°,
OC⊥AB时,∠AOD=60°,
即∠AOD角度所有可能的值为:30°、45°、60°、75°.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020?陕西)如图,AC⊥BC,直线EF经过点C,若∠1=35°,则∠2的大小为( )
A.65° B.55° C.45° D.35°
2.(2020春?丛台区校级月考)如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.两点之间,线段最短
3.(2020春?高州市期中)如图,直线AB⊥CD于O,直线EF交AB于O,∠COF=70°,则∠AOE等于( )
A.20° B.30° C.35° D.70°
4.(2020春?文水县期末)如图,直线AB,CD相交于点O,下列条件中能说明AB⊥CD的有( )
①∠AOD=90°;
②∠AOD=∠AOC;
③∠AOC+∠BOC=180°;
④∠AOC+∠BOD=180°.
A.1个 B.2个 C.3个 D.4个
5.(2020春?抚顺县期末)O为直线AB上一点,OC⊥OD,若∠1=40°,则∠2=( )
A.30° B.40° C.50° D.60°
6.(2020?南海区校级模拟)如图,CA⊥AB,EA⊥AD,已知∠DAB=45°,那么∠EAC的大小是( )
A.50° B.45° C.30° D.60°
7.(2020春?澄迈县期末)如图,三条直线相交于点O.若CO⊥AB,∠1=34°,则∠2等于( )
A.34° B.45° C.56° D.60°
8.(2020春?孝义市期末)下列各图中,过直线l外的点P画直线l的垂线,三角尺操作正确的是( )
A. B.
C. D.
9.(2020春?江汉区月考)如图,AD⊥AC交BC的延长线于点D,AE⊥BC交BC的延长线于点E,CF⊥AB于点F,则图中能表示点A到直线BC的距离的是( )
A.AD的长度 B.AE的长度 C.AC的长度 D.CF的长度
10.(2019秋?仁寿县期末)如图,O为直线AB上一点,OC⊥OD,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论:①∠DOG+∠BOE=180°; ②∠AOE﹣∠DOF=45°;③∠EOD+∠COG=180°; ④∠AOE+∠DOF=90°.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020秋?肇源县期末)两条直线相交所构成的四个角,其中:①有三个角都相等;②有一对对顶角相等;③有一个角是直角;④有一对邻补角相等,能判定这两条直线垂直的有 .
12.(2020春?黄埔区期末)如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠AOD=118°,则∠EOC的度数为 .
13.(2020秋?香坊区校级期中)如图,直线AB⊥CD,EF经过点O,∠2=2∠1,则∠3= °.
14.(2020秋?南岗区校级期中)已知,∠AOB和∠BOC互为邻补角,且∠BOC:∠AOB=4:1,射线OD平分∠AOB,射线OE⊥OD,则∠BOE= .
15.(2020春?太平区期末)关于垂线,小明给出了下面三种说法:①两条直线相交,所构成的四个角中有一个角是直角,那么这两条直线互相垂直;②两条直线的交点叫垂足;③直线AB⊥CD,也可以说成CD⊥AB.其中正确的有 (填序号).
16.(2020春?鱼台县期末)如图,村庄A到公路BC的最短距离是AD的长,其根据是 .
17.(2020春?东城区校级期末)如图,∠C=90°,线段AB=15cm,线段AD=12cm,线段AC=9cm,则点A到BC的距离为 cm.
18.(2020春?岳阳期末)如图,在三角形ABC中,∠ABC=90°,BD⊥AC,垂足为点D,AB=5,BC=12,AC=13,下列结论正确的是 .(写出所有正确结论的序号)
①∠ADB=90°;
②∠A=∠DBC;
③点C到直线BD的距离为线段CB的长度;
④点B到直线AC的距离为6013.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020春?赣州期末)如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
20.(2020秋?长春期末)如图,直线AB与直线MN相交,交点为O,OC⊥AB,OA平分∠MOD,若∠BON=20°,求∠COD的度数.
21.(2019秋?姜堰区期末)如图,直线AB、CD相交于点O,OM⊥AB,∠1=∠2.
(1)求∠NOD的度数;
(2)若∠AOD=3∠1,求∠AOC和∠MOD的度数.
22.(2020秋?香坊区校级期中)如图,直线AB、CD相交于点O,OE平分∠AOC,OF⊥OE于O,且∠DOF=74°,求∠BOD的度数.
23.(2019秋?翠屏区期末)如图,射线OC、OD把∠AOB分成三个角,且度数之比是∠AOC:∠COD:∠DOB=2:3:4,射线OM平分∠AOC,射线ON平分∠BOD,且OM⊥ON.
(1)求∠COD的度数;
(2)求∠AOB的补角的度数.
24.(2019秋?市中区期末)将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图(1),若∠BOD=35°,则∠AOC= ;若∠AOC=135°,则∠BOD= ;(直接写出结论即可)
(2)如图(2),若∠AOC=140°,则∠BOD= ;(直接写出结论即可)
(3)猜想∠AOC与∠BOD的大小关系,并结合图(1)说明理由;
(4)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当锐角∠AOD等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD角度所有可能的值,不用说明理由.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】∵AC⊥BC,
∴∠ACB=90°,
∵∠1+∠ACB+∠2=180°,
∴∠2=180°﹣90°﹣35°=55°,
故选:B.
2.【解析】如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是在同一平面内,过一点有且只有一条直线与已知直线垂直,
故选:C.
3.【解析】∵AB⊥CD,
∴∠COB=90°,
∵∠COF=70°,
∴∠BOF=90°﹣70°=20°,
∴∠AOE=20°,
故选:A.
4.【解析】①∠AOD=90°可以判定两直线垂直,故此选项符合题意;
②∠AOD和∠AOC是邻补角,邻补角相等和又是180°,所以可以得到∠AOC=90°,能判定垂直,故此选项符合题意;
③∠AOC和∠BOC是邻补角,邻补角的和是180°,不能判定垂直,故此选项不符合题意;
④∠AOC和∠BOD是对顶角,对顶角相等,和又是180°,所以可得到∠AOC=90°,故此选项符合题意.
综上所述,①②④共3个正确,
故选:C.
5.【解析】∵OC⊥OD,
∴∠COD=90°,
∴∠1+∠2=90°,
∵∠1=40°,
∴∠2=90°﹣40°=50°,
故选:C.
6.【解析】∵CA⊥AB,
∴∠CAD+∠DAB=∠CAB=90°,
∵∠DAB=45°,
∴∠CAD=45°,
∵EA⊥AD,
∴∠EAD=90°,
∴∠EAC=90°﹣∠CAD=90°﹣45°=45°,
故选:B.
7.【解析】∵CO⊥AB,
∴∠COB=90°,
∵∠1=34°,
∴∠2=180°﹣90°﹣34°=56°,
故选:C.
8.【解析】用直角三角板的一条直角边与l重合,另一条直角边过点P后沿直角边画直线,
∴C选项的画法正确,
故选:C.
9.【解析】图中能表示点A到直线BC的距离的是AE的长度,
故选:B.
10.【解析】∵OE平分∠AOC,OG平分∠BOC,
∴可设∠AOE=∠COE=α,∠BOG=∠COG=β,
∵O为直线AB上一点,
∴∠AOB=180°,
∴2α+2β=180°,
∴α+β=90°,∠EOG=90°.
∵∠DOC=90°,
∴∠DOG=∠COE=90°﹣∠COG=α,
∴∠BOD=∠DOG﹣∠BOG=α﹣β.
∵OF平分∠BOD,
∴∠BOF=∠DOF=12(α﹣β).
①∵∠DOG=α=∠AOE,∠AOE+∠BOE=180°,
∴∠DOG+∠BOE=180°,
故本选项结论正确;
②∵∠AOE=α,∠DOF=12(α﹣β),
∴∠AOE﹣∠DOF=α-12(α﹣β)=12(α+β)=45°,
故本选项结论正确;
③∵∠EOD=∠EOG+∠GOD=90°+α,∠COG=β,
∴∠EOD+∠COG=90°+α+β=180°,
故本选项结论正确;
④∵∠AOE+∠DOF=α+12(α﹣β)=32α-12β=32α-12(90°﹣α)=2α﹣45°,
∴当α=67.5°时,∠AOE+∠DOF=90°,
但是题目没有α=67.5°的条件,
故本选项结论错误.
综上所述,正确的有:①②③共3个.
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】两条直线相交所构成的四个角,
①因为有三个角都相等,都等于90°,所以能判定这两条直线垂直;
②因为有一对对顶角相等,但不一定等于90°,所以不能判定这两条直线垂直;
③有一个角是直角,能判定这两条直线垂直;
④因为一对邻补角相加等于180°,这对邻补角又相等都等于90°,所以能判定这两条直线垂直;
故答案为:①③④.
12.【解析】∵∠AOD=118°,
∴∠BOC=∠AOD=118°,
∵EO⊥AB,
∴∠BOE=90°,
∴∠EOC=∠BOC﹣∠BOE=28°,
故答案为:28°.
13.【解析】∵AB⊥CD,
∴∠1+∠2=90°,
又∵∠2=2∠1,
∴3∠1=90°,
∴∠1=30°,
∴∠3=∠1=30°,
故答案为:30.
14.【解析】∵∠AOB和∠BOC互为邻补角,
∴∠AOB+∠BOC=180°,
又∵∠BOC:∠AOB=4:1,
∴∠BOC=180°×45=144°,∠AOB=180°×15=36°,
∵射线OD平分∠AOB,
∴∠AOD=∠BOD=12∠AOB=18°,
∵OE⊥OD,
∴∠DOE=90°,
如图1,∠BOE=∠DOE﹣∠BOD=90°﹣18°=72°,
如图2,∠BOE=∠DOE+∠BOD=90°+18°=108°,
故答案为:72°或108°.
15.【解析】①两条直线相交,所构成的四个角中有一个角是直角,那么这两条直线互相垂直,故原题说法正确;
②两条直线的交点叫交点,故原题说法错误;
③直线AB⊥CD,也可以说成CD⊥AB,故原题说法正确,
正确的说法有2个,
故答案为:①③.
16.【解析】村庄A到公路BC的最短距离是AD的长,其根据是垂线段最短,
故答案为:垂线段最短.
17.【解析】因为∠C=90°,
所以AC⊥BC,
所以A到BC的距离是AC,
因为线段AC=9cm,
所以点A到BC的距离为9cm.
故答案为:9.
18.【解析】①∵BD⊥AC,
∴∠ADB=90°,故①正确;
②∵∠ABD+∠A=90°,∠ABD+∠DBC=90°,
∴∠A=∠DBC,故②正确;
③点C到直线BD的距离为线段CD的长度,故③错误;
④点B到直线AC的距离为12×5×12×2÷13=6013,故④正确.
故答案为:①②④.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】如图所示
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
20.【解析】∵∠BON=20°,
∴∠AOM=20°,
∵OA平分∠MOD,
∴∠AOD=∠MOA=20°,
∵OC⊥AB,
∴∠AOC=90°,
∴∠COD=90°﹣20°=70°.
21.【解析】证明:(1)∵OM⊥AB,
∴∠AOM=∠BOM=90°,
∴∠1+∠AOC=90°,
∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴∠NOD=180°﹣∠CON=180°﹣90°=90°;
(2)∵∠AOD=3∠1,
∴∠NOD=2∠1=90°,
解得:∠1=45°,
∴∠AOC=∠AOM﹣∠1=90°﹣45°=45°;
∴∠BOD=90°﹣45°=45°,
∴∠MOD=∠BOD+∠BOM=45°+90°=135°.
故答案为:(1)90°; (2)45°,135°.
22.【解析】∵OF⊥OE,
∴∠EOF=90°,
又∵∠COE+∠EOF+∠DOF=180°,∠DOF=74°,
∴∠COE=180°﹣90°﹣74°=16°,
∵OE平分∠AOC,
∴∠AOC=2∠COE=32°=∠BOD,
答:∠BOD的度数为32°.
23.【解析】(1)设∠AOC=2x,∠COD=3x,∠DOB=4x,则∠AOB=9x,
∵OM平分∠AOC,ON平分∠DOB,
∴∠MOC=x,∠NOD=2x,
∴∠MON=x+3x+2x=6x,
又∵OM⊥ON,
∴∠MON=90°,
即6x=90°,
解得x=15°,
∴∠COD=45°;
(2)∵∠AOB=9×15°=135°,
∴∠AOB的补角的度数为45°.
24.【解析】(1)若∠BOD=35°,
∵∠AOB=∠COD=90°,
∴∠AOC=∠AOB+∠COD﹣∠BOD=90°+90°﹣35°=145°,
若∠AOC=135°,
则∠BOD=∠AOB+∠COD﹣∠AOC=90°+90°﹣135°=45°;
故答案为:145°;45°;
(2)如图2,若∠AOC=140°,
则∠BOD=360°﹣∠AOC﹣∠AOB﹣∠COD
=360°﹣140°﹣90°﹣90°
=40°;
故答案为:40°;
(3)∠AOC与∠BOD互补.
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOD+∠BOD+∠BOC=180°.
∵∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180°,
即∠AOC与∠BOD互补.
(4)OD⊥AB时,∠AOD=30°,
CD⊥OB时,∠AOD=45°,
CD⊥AB时,∠AOD=75°,
OC⊥AB时,∠AOD=60°,
即∠AOD角度所有可能的值为:30°、45°、60°、75°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
