2020——2021学年人教版 七年级数学下册 5.3 平行线的性质 课时作业(Word版 含答案)
文档属性
| 名称 | 2020——2021学年人教版 七年级数学下册 5.3 平行线的性质 课时作业(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 381.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 00:00:00 | ||
图片预览

文档简介
人教版 七年级数学下册 5.3 平行线的性质 课时作业
一、选择题
1. 如图,直线l1∥l2,∠1=55°,∠2=65°,则∠3为( )
A. 50° B. 55° C. 60° D. 65°
2. 下列图形中,由,能得到的是( )
A B C D
3. 如图,直线AB∥CD,则下列结论正确的是 ( )
A.∠1=∠2 B.∠3=∠4
C.∠1+∠3=180° D.∠3+∠4=180°
4. (2020·岳阳)如图,,,,则的度数是( )
A. B. C. D.
5. (2020·遵义)一副直角三角板如图放置,使两三角板的斜边互相平行,每块三角板的直角顶点都在另一三角板的斜边上,则∠1的度数为( )
A.30° B.45° C.55° D.60°
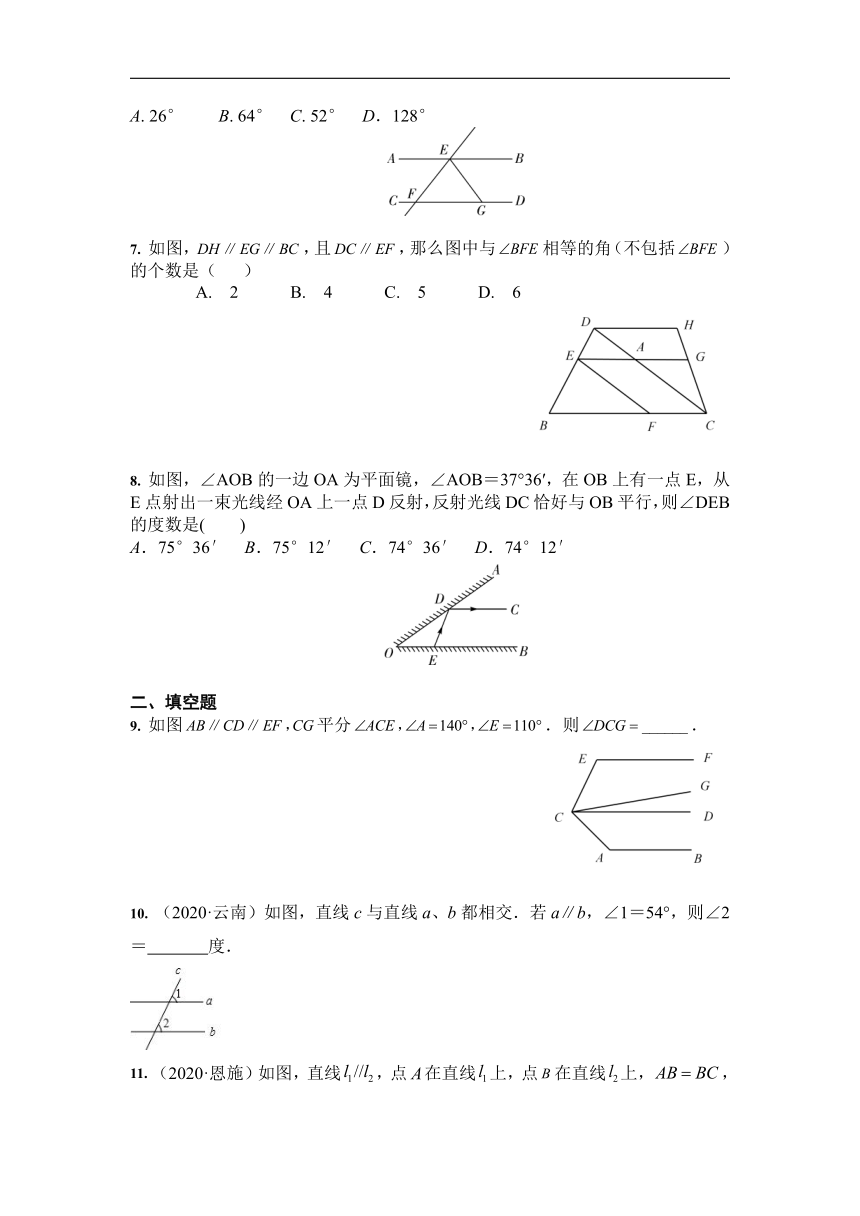
6. 如图,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=52°,则∠EGF等于( )
A. 26° B. 64° C. 52° D.128°
7. 如图,,且,那么图中与相等的角(不包括)的个数是( )
A. 2 B. 4 C. 5 D. 6
8. 如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )
A.75°36′ B.75°12′ C.74°36′ D.74°12′
二、填空题
9. 如图平分.则.
10. (2020·云南)如图,直线c与直线a、b都相交.若a∥b,∠1=54°,则∠2= 度.
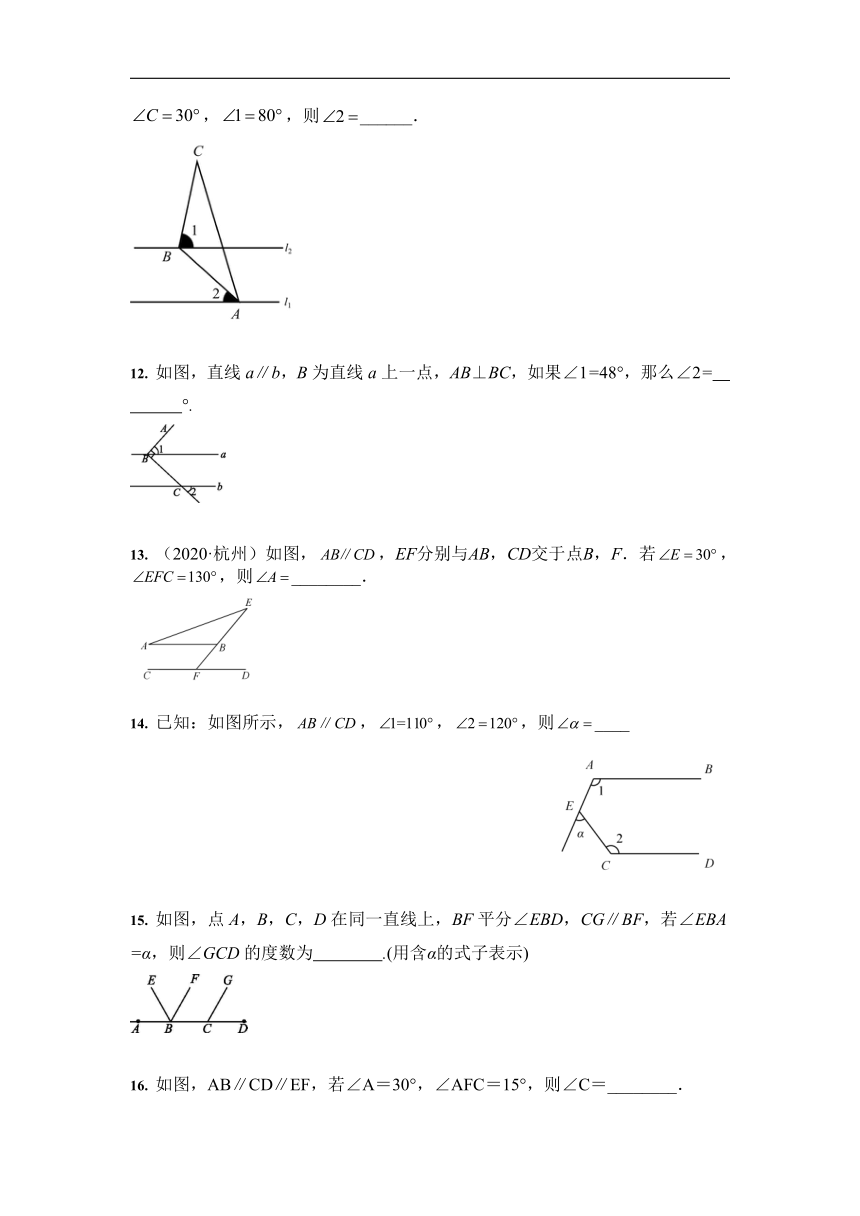
11. (2020·恩施)如图,直线,点在直线上,点在直线上,,,,则______.
12. 如图,直线a∥b,B为直线a上一点,AB⊥BC,如果∠1=48°,那么∠2= °.?
13. (2020·杭州)如图,,EF分别与AB,CD交于点B,F.若,,则________.
14. 已知:如图所示,,,,则____
15. 如图,点A,B,C,D在同一直线上,BF平分∠EBD,CG∥BF,若∠EBA=α,则∠GCD的度数为 .(用含α的式子表示)?
16. 如图,AB∥CD∥EF,若∠A=30°,∠AFC=15°,则∠C=________.
三、解答题
17. 如图,中于,,交与.过上任意一点,作于,求证:.
18. 如下图,,,,求的度数.
人教版 七年级数学下册 5.3 平行线的性质 课时作业-答案
一、选择题
1. 【答案】C 【解析】
?∠3=180°-∠4-∠5=180°-55°-65°=60°.
解图
2. 【答案】B.
3. 【答案】D
4. 【答案】D
【解析】∵AB⊥DA,CD⊥DA,∴CD∥BA,∴∠B+∠C=180°,∴∠C=180°-56°=124°.故选D.
5. 【答案】B
【解析】本题考查平行线的性质.由两三角板的斜边互相平行,根据两直线平行内错角相等得∠1=45°,故选B.
6. 【答案】B 【解析】根据题意知∠EFG=52°,AB∥CD,∴∠BEF=180°-52°=128°,而EG平分∠BEF,∴∠BEG=∠BEF=64°,∴∠EGF=∠BEG=64°.
7. 【答案】C
【解析】本题考查平行线的性质,由图形找到与相等的角有,,,,
8. 【答案】B 【解析】根据平面镜反射原理可知,∠ADC=∠ODE,∵DC∥OB,∴∠ADC=∠AOE,∴∠ODE=∠AOE=37°36′,∴∠DEB=∠ODE+∠AOE=37°36′+37°36′=75°12′,故选B.
二、填空题
9. 【答案】.
【解析】∵,∴,
同理
∴
∵平分
∴
∴
10. 【答案】54
【解析】本题考查了平行线的性质,直接利用平行线的性质进而分析得出答案.
11. 【答案】40°
【解析】
∵AB=BC,∠C=,
∴∠CAB=,
∴∠CBA=,
∵∠1=,
∴∠EBA=,
∵
∴
故答案为:.
12. 【答案】42 [解析] 因为AB⊥BC,∠1=48°,所以∠1的余角为42°.因为直线a∥b,所以∠2=42°.
13. 【答案】20°
【解析】本题考查了平行线的性质以及三角形的内角和定理,因为AB∥CD,所以∠ABE=∠EFC=130°.在△ABE中,因为∠A+∠E+∠ABE=180°,所以∠A=180°-∠E-∠ABE=180°-30°-130°=20°,因此本题答案为20°.
14. 【答案】
【解析】如图所示,过点作的平行线,
则,
∵,
∴
∴
15. 【答案】90°-α [解析] ∵∠EBA=α,∠EBA+∠EBD=180°,∴∠EBD=180°-α.∵BF平分∠EBD,∴∠FBD=∠EBD=(180°-α)=90°-α.∵CG∥BF,∴∠GCD=∠FBD=90°-α.
16. 【答案】15° 【解析】由两直线平行,内错角相等,可得∠A=∠AFE=30°,∠C=∠CFE,由∠AFC=15°,可得∠CFE=∠C=∠AFE-∠AFC=15°.
三、解答题
17. 【答案】
∵,
∴
∴,
∵,
∴,
∴
18. 【答案】
【解析】如图,过点作,
∵,∴,
又∵,
∴
∴,
∴.
一、选择题
1. 如图,直线l1∥l2,∠1=55°,∠2=65°,则∠3为( )
A. 50° B. 55° C. 60° D. 65°
2. 下列图形中,由,能得到的是( )
A B C D
3. 如图,直线AB∥CD,则下列结论正确的是 ( )
A.∠1=∠2 B.∠3=∠4
C.∠1+∠3=180° D.∠3+∠4=180°
4. (2020·岳阳)如图,,,,则的度数是( )
A. B. C. D.
5. (2020·遵义)一副直角三角板如图放置,使两三角板的斜边互相平行,每块三角板的直角顶点都在另一三角板的斜边上,则∠1的度数为( )
A.30° B.45° C.55° D.60°
6. 如图,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=52°,则∠EGF等于( )
A. 26° B. 64° C. 52° D.128°
7. 如图,,且,那么图中与相等的角(不包括)的个数是( )
A. 2 B. 4 C. 5 D. 6
8. 如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )
A.75°36′ B.75°12′ C.74°36′ D.74°12′
二、填空题
9. 如图平分.则.
10. (2020·云南)如图,直线c与直线a、b都相交.若a∥b,∠1=54°,则∠2= 度.
11. (2020·恩施)如图,直线,点在直线上,点在直线上,,,,则______.
12. 如图,直线a∥b,B为直线a上一点,AB⊥BC,如果∠1=48°,那么∠2= °.?
13. (2020·杭州)如图,,EF分别与AB,CD交于点B,F.若,,则________.
14. 已知:如图所示,,,,则____
15. 如图,点A,B,C,D在同一直线上,BF平分∠EBD,CG∥BF,若∠EBA=α,则∠GCD的度数为 .(用含α的式子表示)?
16. 如图,AB∥CD∥EF,若∠A=30°,∠AFC=15°,则∠C=________.
三、解答题
17. 如图,中于,,交与.过上任意一点,作于,求证:.
18. 如下图,,,,求的度数.
人教版 七年级数学下册 5.3 平行线的性质 课时作业-答案
一、选择题
1. 【答案】C 【解析】
?∠3=180°-∠4-∠5=180°-55°-65°=60°.
解图
2. 【答案】B.
3. 【答案】D
4. 【答案】D
【解析】∵AB⊥DA,CD⊥DA,∴CD∥BA,∴∠B+∠C=180°,∴∠C=180°-56°=124°.故选D.
5. 【答案】B
【解析】本题考查平行线的性质.由两三角板的斜边互相平行,根据两直线平行内错角相等得∠1=45°,故选B.
6. 【答案】B 【解析】根据题意知∠EFG=52°,AB∥CD,∴∠BEF=180°-52°=128°,而EG平分∠BEF,∴∠BEG=∠BEF=64°,∴∠EGF=∠BEG=64°.
7. 【答案】C
【解析】本题考查平行线的性质,由图形找到与相等的角有,,,,
8. 【答案】B 【解析】根据平面镜反射原理可知,∠ADC=∠ODE,∵DC∥OB,∴∠ADC=∠AOE,∴∠ODE=∠AOE=37°36′,∴∠DEB=∠ODE+∠AOE=37°36′+37°36′=75°12′,故选B.
二、填空题
9. 【答案】.
【解析】∵,∴,
同理
∴
∵平分
∴
∴
10. 【答案】54
【解析】本题考查了平行线的性质,直接利用平行线的性质进而分析得出答案.
11. 【答案】40°
【解析】
∵AB=BC,∠C=,
∴∠CAB=,
∴∠CBA=,
∵∠1=,
∴∠EBA=,
∵
∴
故答案为:.
12. 【答案】42 [解析] 因为AB⊥BC,∠1=48°,所以∠1的余角为42°.因为直线a∥b,所以∠2=42°.
13. 【答案】20°
【解析】本题考查了平行线的性质以及三角形的内角和定理,因为AB∥CD,所以∠ABE=∠EFC=130°.在△ABE中,因为∠A+∠E+∠ABE=180°,所以∠A=180°-∠E-∠ABE=180°-30°-130°=20°,因此本题答案为20°.
14. 【答案】
【解析】如图所示,过点作的平行线,
则,
∵,
∴
∴
15. 【答案】90°-α [解析] ∵∠EBA=α,∠EBA+∠EBD=180°,∴∠EBD=180°-α.∵BF平分∠EBD,∴∠FBD=∠EBD=(180°-α)=90°-α.∵CG∥BF,∴∠GCD=∠FBD=90°-α.
16. 【答案】15° 【解析】由两直线平行,内错角相等,可得∠A=∠AFE=30°,∠C=∠CFE,由∠AFC=15°,可得∠CFE=∠C=∠AFE-∠AFC=15°.
三、解答题
17. 【答案】
∵,
∴
∴,
∵,
∴,
∴
18. 【答案】
【解析】如图,过点作,
∵,∴,
又∵,
∴
∴,
∴.
