2020-2021学年人教版数学七年级下册5.2.2《平行线的判定》课件(24张)
文档属性
| 名称 | 2020-2021学年人教版数学七年级下册5.2.2《平行线的判定》课件(24张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 522.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 00:00:00 | ||
图片预览



文档简介
平行线的判定
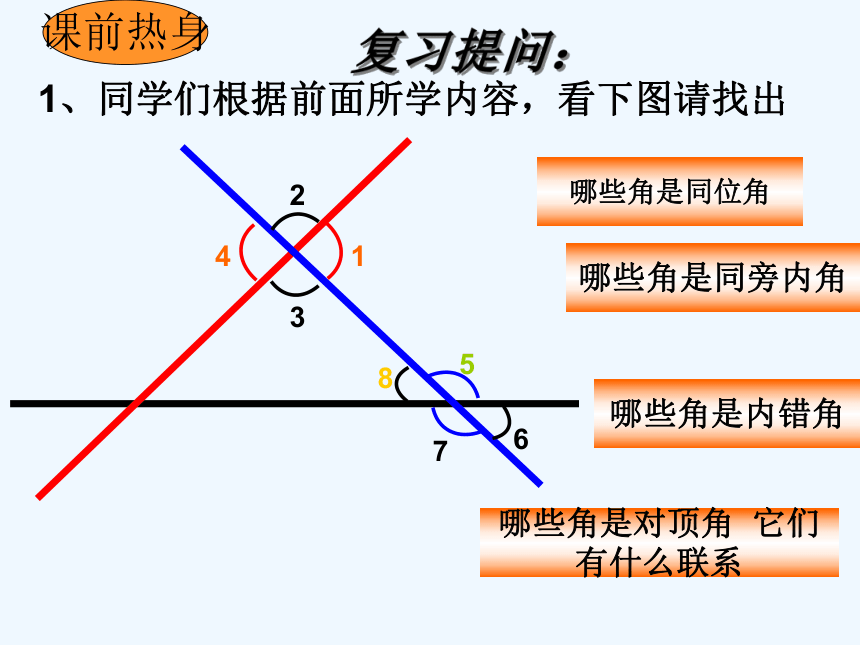
1、同学们根据前面所学内容,看下图请找出
哪些角是内错角
哪些角是同位角
哪些角是同旁内角
哪些角是对顶角 它们有什么联系
2
3
4
1
5
7
8
6
复习提问:
课前热身
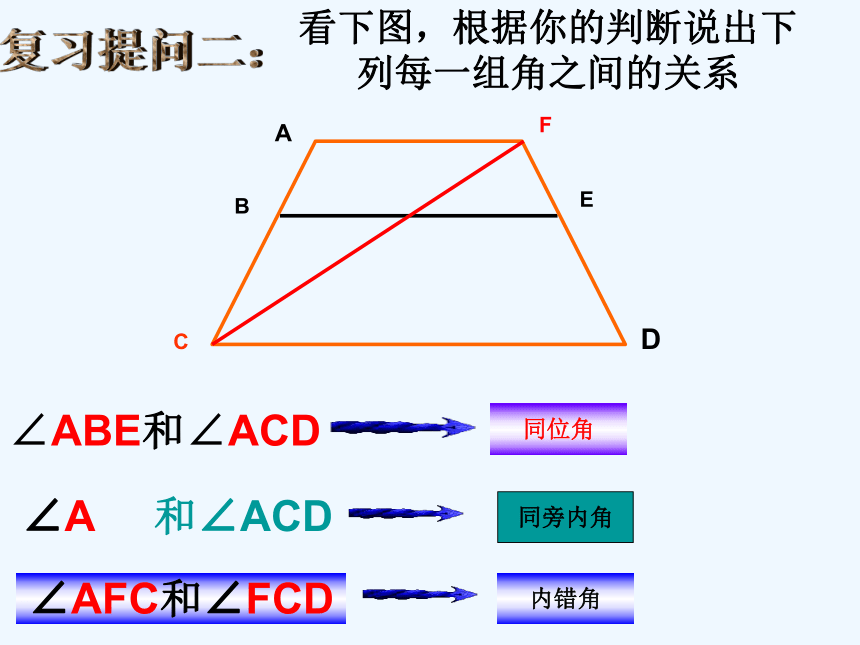
看下图,根据你的判断说出下列每一组角之间的关系
∠ABE和∠ACD
∠A 和∠ACD
∠AFC和∠FCD
A
B
C
F
E
D
同位角
同旁内角
内错角
复习提问二:
复习提问三:
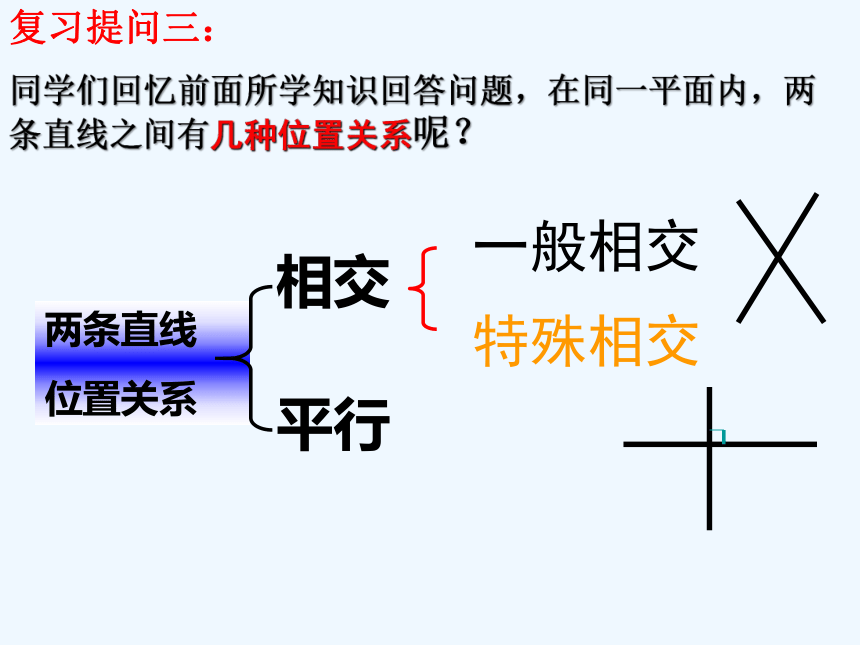
同学们回忆前面所学知识回答问题,在同一平面内,两条直线之间有几种位置关系呢?
一般相交
特殊相交
两条直线
位置关系
相交
平行
判断下列语句是否正确:
(1) 两条直线不相交,就叫做平行线. ( )
(2) 与一条直线平行的直线只有一条. ( )
(3) 如果两条直线a、b都和直线c平行,
那么直线a、b就平行. ( )
×
√
×
热身训练
判定两条直线平行的方法有两种:
定义:在同一平面内,不相交的两条直线叫平行线.
平行公理的推论
同学们可以想一想?
除应用以上两种方法以外,是否还有其它方法呢?
如果两条直线同平行于一条直线,那么两条直线平行.
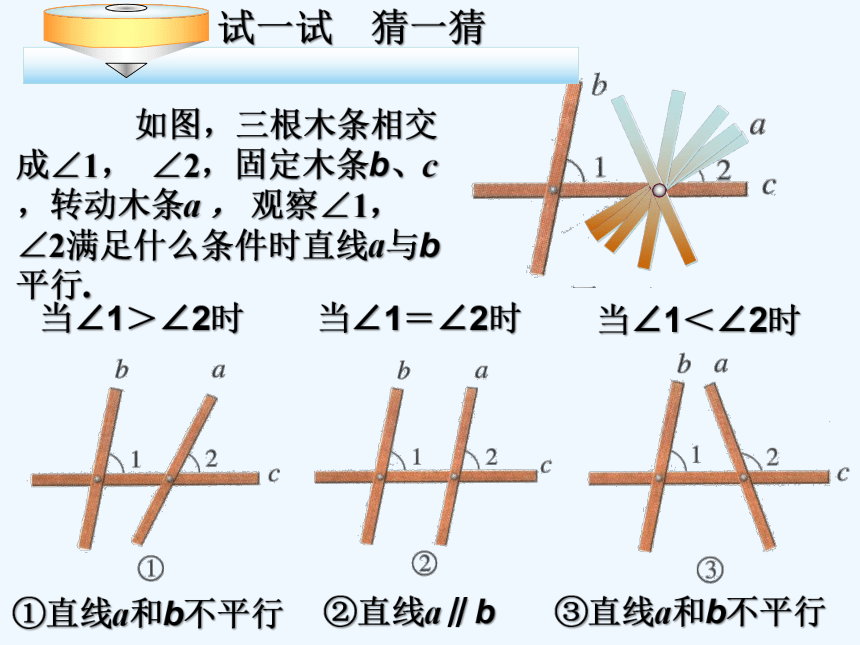
如图,三根木条相交成∠1, ∠2,固定木条b、c,转动木条a , 观察∠1, ∠2满足什么条件时直线a与b平行.
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行
②直线a∥b
③直线a和b不平行
试一试 猜一猜
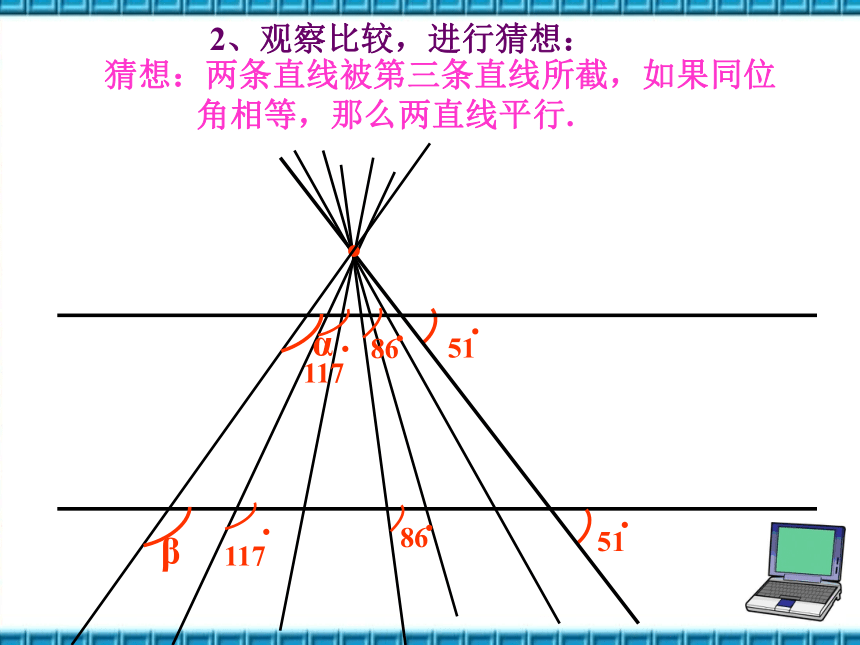
猜想:两条直线被第三条直线所截,如果同位
角相等,那么两直线平行.
51
.
51
.
86
.
86
.
117
.
117
.
.
α
β
2、观察比较,进行猜想:
126
.
107
.
168
.
126
.
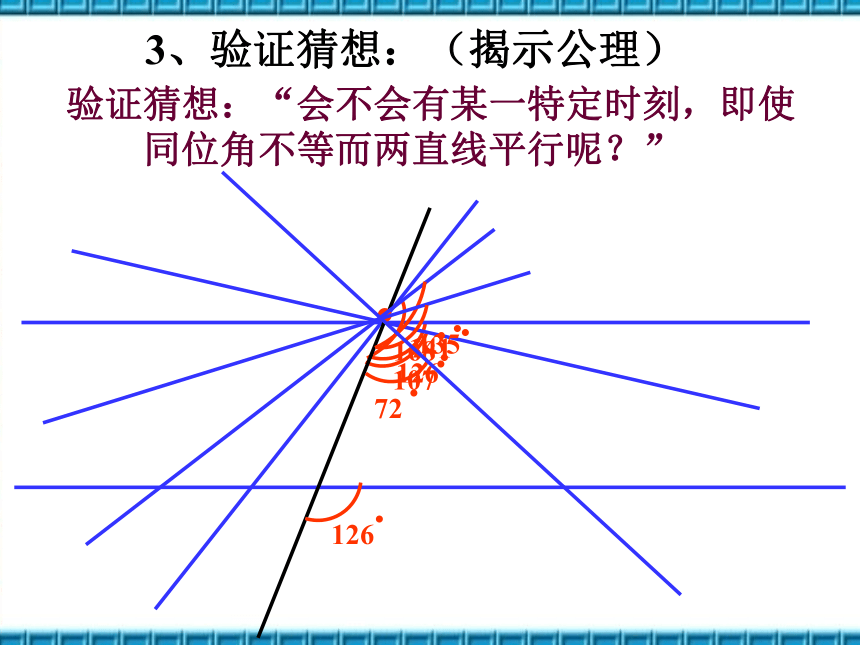
验证猜想:“会不会有某一特定时刻,即使
同位角不等而两直线平行呢?”
.
141
.
135
.
72
.
3、验证猜想:(揭示公理)
两条直线被第三条直线所截,如果同
位角相等,那么这两条直线平行.
简单说成:
同位角相等、两直线平行
判定两条直线平行的公理:
3、验证猜想:(揭示公理)
α
β
a
b
c
推理过程:
∵∠α = ∠ β(已知)
∴a ∥ b(同位角相等、两直线平行)
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截 ,如果同位角相等,那么这两条直线平行.简单地说,同位角相等,两直线平行.
4
1
2
3
A
B
C
E
F
D
5
H
G
如图,哪两个角相等能判定直线AB∥CD?
如果 , 能判定哪两条直线平行?
∠1 =∠2
∠3=∠4
AB∥CD
EF∥GH
1
4
3
2
A
D
C
B
∠3 =∠4
∠2 =∠5
EF∥GH
如图,已知∠1+∠2=180?,AB与CD平行吗?为什么?
例1
A
B
C
D
E
F
1
2
3
例2 已知:如图,ABC、CDE都是直线,
且∠1=∠2,∠1=∠C,
求证:AC∥FD.
∵ ∠1 = ∠2,
∠1 = ∠C (已知)
∴ ∠2=∠C (等量代换)
∴ AC∥FD (同位角相等,两直线平行)
F
E
B
C
D
A
2
1
证明:
如图,已知∠1=∠2,AB与CD平行吗?为什么?
例3
A
B
C
D
E
F
1
2
3
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.简单地说,内错角相等,两直线平行.
4
1
2
3
A
B
C
E
F
D
5
H
G
如图,哪两个角相等能判定直线AB∥CD?
如果 , 能判定哪两条直线平行?
∠3 =∠2
∠3=∠4或∠1=∠4
AB∥CD
AB∥CD
1
4
3
2
A
D
C
B
∠5 =∠6
∠4 =∠5
EF∥GH
6
例4 已知:如图,∠DAB被AC平分,
且∠1=∠3,
A
B
C
D
1
2
3
求证:AB∥CD.
∵ ∠DAB被AC平分 (已知)
∴ ∠1=∠2 (角平分线定义)
∵ ∠1=∠3 (已知)
∴ ∠2=∠3 (等量代换)
∴ AB∥CD ( 内错角相等,两直线平行 )
证明:
如图,已知∠1+∠2=180?,AB与CD平行吗?为什么?
例5
A
B
C
D
E
F
1
2
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.简单地说,同旁内角互补,两直线平行.
3
1
2
1.如图,直线 被直线 所截.
(1)若 ,则 与 平行吗?根据什么?
(2)若 ,则 与 平行吗?根据什么?
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
a
b
c
1
2
∵ b⊥a
∴∠2=90°
(垂直的定义)
∴b∥c.
(同位角相等,两直线平行)
∴∠1=90°
(垂直的定义)
∵ c ⊥a
∴∠1=∠2
想一想
判定两直线平行有哪些方法?
理由:
平行
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)
a
b
c
1
2
方法2:
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)
a
b
c
1
2
方法3:
结论
在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线平行.
b
c
1
2
a
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.在同一平面内,如果两条直线都垂直于
同一条直线,那么这两条直线平行.
判定两条直线是否平行的方法有:
小结
这节课我们学了什么?
平行线判定方法1:同位角相等,两直线平行.
平行线判定方法2:内错角相等,两直线平行.
平行线判定方法2:同旁内角互补,两直线平行.
你记住了吗?
1、同学们根据前面所学内容,看下图请找出
哪些角是内错角
哪些角是同位角
哪些角是同旁内角
哪些角是对顶角 它们有什么联系
2
3
4
1
5
7
8
6
复习提问:
课前热身
看下图,根据你的判断说出下列每一组角之间的关系
∠ABE和∠ACD
∠A 和∠ACD
∠AFC和∠FCD
A
B
C
F
E
D
同位角
同旁内角
内错角
复习提问二:
复习提问三:
同学们回忆前面所学知识回答问题,在同一平面内,两条直线之间有几种位置关系呢?
一般相交
特殊相交
两条直线
位置关系
相交
平行
判断下列语句是否正确:
(1) 两条直线不相交,就叫做平行线. ( )
(2) 与一条直线平行的直线只有一条. ( )
(3) 如果两条直线a、b都和直线c平行,
那么直线a、b就平行. ( )
×
√
×
热身训练
判定两条直线平行的方法有两种:
定义:在同一平面内,不相交的两条直线叫平行线.
平行公理的推论
同学们可以想一想?
除应用以上两种方法以外,是否还有其它方法呢?
如果两条直线同平行于一条直线,那么两条直线平行.
如图,三根木条相交成∠1, ∠2,固定木条b、c,转动木条a , 观察∠1, ∠2满足什么条件时直线a与b平行.
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行
②直线a∥b
③直线a和b不平行
试一试 猜一猜
猜想:两条直线被第三条直线所截,如果同位
角相等,那么两直线平行.
51
.
51
.
86
.
86
.
117
.
117
.
.
α
β
2、观察比较,进行猜想:
126
.
107
.
168
.
126
.
验证猜想:“会不会有某一特定时刻,即使
同位角不等而两直线平行呢?”
.
141
.
135
.
72
.
3、验证猜想:(揭示公理)
两条直线被第三条直线所截,如果同
位角相等,那么这两条直线平行.
简单说成:
同位角相等、两直线平行
判定两条直线平行的公理:
3、验证猜想:(揭示公理)
α
β
a
b
c
推理过程:
∵∠α = ∠ β(已知)
∴a ∥ b(同位角相等、两直线平行)
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截 ,如果同位角相等,那么这两条直线平行.简单地说,同位角相等,两直线平行.
4
1
2
3
A
B
C
E
F
D
5
H
G
如图,哪两个角相等能判定直线AB∥CD?
如果 , 能判定哪两条直线平行?
∠1 =∠2
∠3=∠4
AB∥CD
EF∥GH
1
4
3
2
A
D
C
B
∠3 =∠4
∠2 =∠5
EF∥GH
如图,已知∠1+∠2=180?,AB与CD平行吗?为什么?
例1
A
B
C
D
E
F
1
2
3
例2 已知:如图,ABC、CDE都是直线,
且∠1=∠2,∠1=∠C,
求证:AC∥FD.
∵ ∠1 = ∠2,
∠1 = ∠C (已知)
∴ ∠2=∠C (等量代换)
∴ AC∥FD (同位角相等,两直线平行)
F
E
B
C
D
A
2
1
证明:
如图,已知∠1=∠2,AB与CD平行吗?为什么?
例3
A
B
C
D
E
F
1
2
3
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.简单地说,内错角相等,两直线平行.
4
1
2
3
A
B
C
E
F
D
5
H
G
如图,哪两个角相等能判定直线AB∥CD?
如果 , 能判定哪两条直线平行?
∠3 =∠2
∠3=∠4或∠1=∠4
AB∥CD
AB∥CD
1
4
3
2
A
D
C
B
∠5 =∠6
∠4 =∠5
EF∥GH
6
例4 已知:如图,∠DAB被AC平分,
且∠1=∠3,
A
B
C
D
1
2
3
求证:AB∥CD.
∵ ∠DAB被AC平分 (已知)
∴ ∠1=∠2 (角平分线定义)
∵ ∠1=∠3 (已知)
∴ ∠2=∠3 (等量代换)
∴ AB∥CD ( 内错角相等,两直线平行 )
证明:
如图,已知∠1+∠2=180?,AB与CD平行吗?为什么?
例5
A
B
C
D
E
F
1
2
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.简单地说,同旁内角互补,两直线平行.
3
1
2
1.如图,直线 被直线 所截.
(1)若 ,则 与 平行吗?根据什么?
(2)若 ,则 与 平行吗?根据什么?
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
a
b
c
1
2
∵ b⊥a
∴∠2=90°
(垂直的定义)
∴b∥c.
(同位角相等,两直线平行)
∴∠1=90°
(垂直的定义)
∵ c ⊥a
∴∠1=∠2
想一想
判定两直线平行有哪些方法?
理由:
平行
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)
a
b
c
1
2
方法2:
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)
a
b
c
1
2
方法3:
结论
在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线平行.
b
c
1
2
a
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.在同一平面内,如果两条直线都垂直于
同一条直线,那么这两条直线平行.
判定两条直线是否平行的方法有:
小结
这节课我们学了什么?
平行线判定方法1:同位角相等,两直线平行.
平行线判定方法2:内错角相等,两直线平行.
平行线判定方法2:同旁内角互补,两直线平行.
你记住了吗?
