2020-2021学年人教版七年级下册数学5.1.1 ---5.1.3同步过关测试题(Word版 含答案)
文档属性
| 名称 | 2020-2021学年人教版七年级下册数学5.1.1 ---5.1.3同步过关测试题(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 419.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 00:00:00 | ||
图片预览




文档简介
相交线
1、下列说法正确的有(
)
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个
B.2个
C.3个
D.4个
2、下列图形中,表示∠1和∠2是对顶角的图形是(
)
3、如图所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于(
)
A.150°
B.180°
C.210°
D.120°
4、如图,三条直线,,相交于点,则( )
A.
B.
C.
D.
5、直线AB、CD交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于(
)
A、38°
B、104°
C、142°
D、144°
6、下列语句错误的有(
)个.
(1)两个角的两边分别在同一条直线上,这两个角互为对顶角
(2)有公共顶点并且相等的两个角是对顶角
(3)如果两个角相等,那么这两个角互补
(4)如果两个角不相等,那么这两个角不是对顶角
A.1
B.2
C.3
D.4
7、如图,平面上三条不同的直线相交最多能构成对顶角的对数是(
)
A.4
B.5
C.6
D.7
7、如图,AB∥CD,AC⊥BC,∠BAC=65°,则∠BCD=______________度。
8、如图所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.
9、如图,当剪子口∠AOB增大15°时,∠COD增大____________。
10、已知∠1与∠2是对顶角,∠1与∠3互为补角,则∠2+∠3=
。
11、如图,直线a,b,c两两相交,∠1=2∠3,∠2=68°,求∠4的度数.
12、如图所示,直线AB与CD相交于点O,∠AOC:∠AOD=2:3,求∠BOD的度数.
13、如图,∠1=∠2,∠1+∠2=162°,求∠3与∠4的度数。
14、如图,O为直线AB上一点,∠BOC
=
3∠AOC,OC平分∠AOD;
⑴
求∠AOC的度数;
⑵
推测OD与AB的位置关系,并说明理由。
15、如图,直线a,b,c两两相交,∠1=2∠3,∠2=68°,求∠4的度数.
5.1.2垂线
选择。
1、与一条已知直线垂直的直线有(
)
A.
1条
B.
2条
C.
3条
D.
无数条
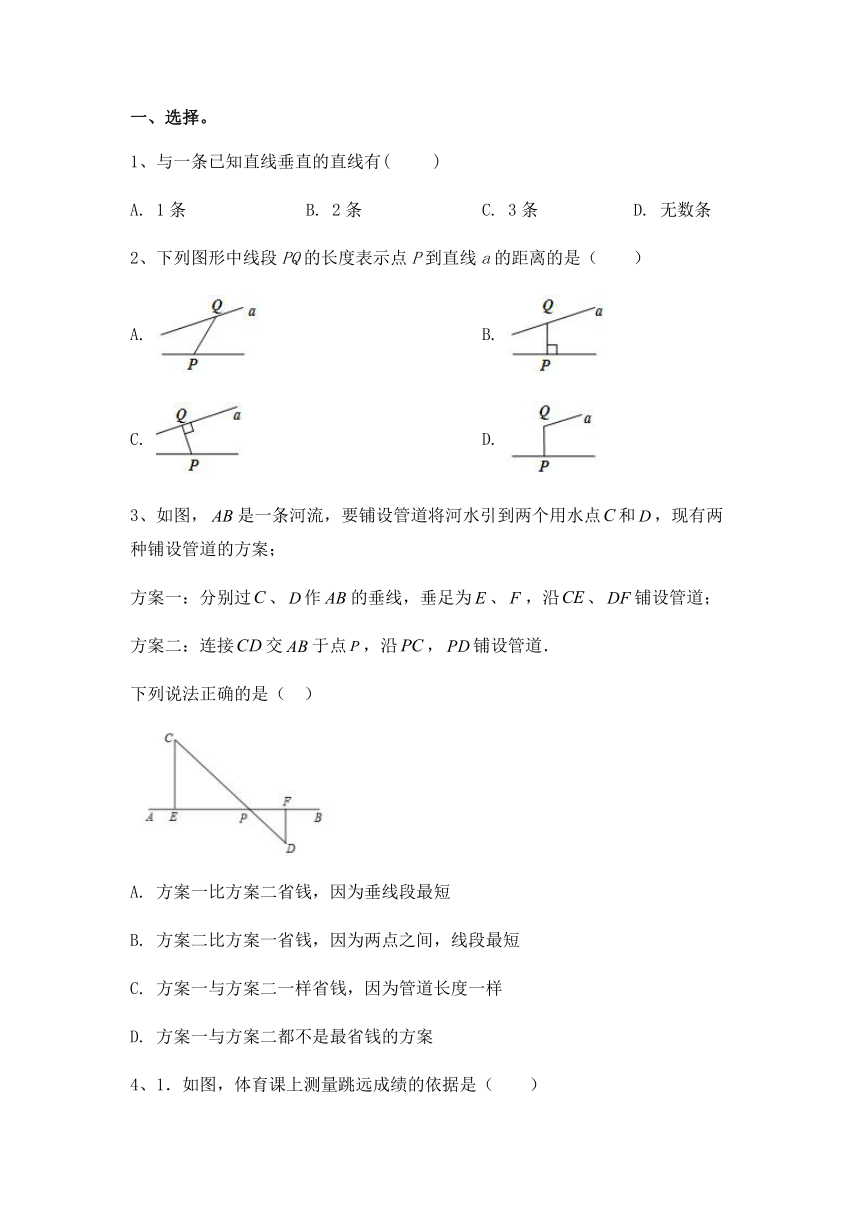
2、下列图形中线段PQ的长度表示点P到直线a的距离的是( )
A.
B.
C.
D.
3、如图,是一条河流,要铺设管道将河水引到两个用水点和,现有两种铺设管道的方案;
方案一:分别过、作的垂线,垂足为、,沿、铺设管道;
方案二:连接交于点,沿,铺设管道.
下列说法正确的是(
)
A.
方案一比方案二省钱,因为垂线段最短
B.
方案二比方案一省钱,因为两点之间,线段最短
C.
方案一与方案二一样省钱,因为管道长度一样
D.
方案一与方案二都不是最省钱的方案
4、1.如图,体育课上测量跳远成绩的依据是(
)
A.平行线间的距离相等
B.两点之间,线段最短
C.垂线段最短
D.两点确定一条直线
5、如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
A.两点之间线段最短
B.点到直线的距离
C.两点确定一条直线
D.垂线段最短
6、在下列生活实例中,数学依据不正确的是(
)
A.在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上,依据的是两点确定一条直线;
B.在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标,依据的是两点之间线段最短;
C.从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,大大节约了路程,依据的是两点之间线段最短;
D.体育课上,体育老师测量跳远距离的时候,测的是落脚脚跟到起跳线的距离,依据的是垂线段最短.
7、体育课上,老师测量跳远成绩的依据是(
)
A.两点确定一条直线
B.两点之间,线段最短
C.垂线段最短
D.平行线间的距离相等
8、如图,点P是直线a外一点,PB⊥a,点A,B,C,D都在直线a上,下列线段中最短的是(
)
A.PA
B.PB
C.PC
D.PD
填空。
9、连接直线外一点与直线上各点的所有线段中,__________最短.
10、如图所示,想在河堤两岸塔建一座桥,搭建方式最短的是_____,理由_____.
11、如图,从D处开渠引水到C处,则渠道CD最短,依据是__________.
12、定点P在直线AB外,动点O在直线AB上移动,当PO最短时,∠POA=_______.这时线段PO所在的直线是直线AB的________,线段PO叫做直线AB的__________.
解答。
如图,要从小河a引水到村庄A,请设计并作出一最短路线,画在图中。
14、如图,AC⊥CD,∠BED=90°.填空:
(1)∠ACD=_____度;
(2)直线AD与BE的位置关系是__________;
(3)点B到直线AD的距离是线段________的长度,点D到直线AB的距离是线段______的长度;
(4)在线段DA,DB,DC中,最短的是线段______;在线段BA,BE,BD中,最短的是线段______,理由是_____________________________________.
15、已知:四点A,B,C,D的位置如图所示,
(1)连接AD;
(2)画射线AB与线段DC的延长线交于点E;
(3)过点B作BF⊥CD于点F.
16、如图,AD⊥BC于点D,EF⊥BC于点F,∠BDG=∠C.试说明∠1=∠2.
17、如图,直线、相交于点,,与的度数之比为.求的度数.
18、(1)如图1,村庄A到公路BC的最短距离是AD,根据是________.
(2)如图2,建筑工人常在一根细绳上拴上一个重物,做成一个“铅锤”,挂铅锤的线总垂直于地面内的任何直线,当这条线贴近墙壁时,说明墙与地面垂直,请说出它的根据是____________________________.
答案
D
2、C
3、A
4、C
D
6、B
7、C
8、B
垂线段
PN,
垂线段最短
垂线段最短
90°
垂线
垂线段
(1)
90
;(2)
互相垂直
;(3)
BE,DC
;(4)
DC,
BE,连结直线外一点与直线上各点的所有线段中,垂线段最短
如图:(1)连接AD,
(2)作射线AB,线段DC,并延长线段DC交于射线AB与E,
(3)过点B作BF⊥CD于点F.
16、∵AD⊥BC于点D,EF⊥BC于点F,∴∠ADB=∠FEC=90°.
∵∠BDG=∠C,∠2+∠BDG=90°,∠1+∠C=90°,∴∠1=∠2.
17、度数为.
18、(1)垂线段最短;
(2)过一点有且只有一条直线与已知直线垂直
5.1.3同位角、内错角、同旁内角
选择。
1、如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.
如果∠1=20°,那么∠2的度数是(
)
A.15°
B.20°
C.25°
D.30°
2、如图,点E在BC的延长线上,下列条件不能判定AB∥CD的是(
)
∠3=∠4
B.
∠B=∠DCE
C.
∠4=∠2
D.
∠D+∠DAB=180°
3、
如图,直线a,b被直线c所截,a∥b,若∠2=45°,则∠1等于( )
A.
125°
B.
130°
C.
135°
D.
145°
4、如图,∠1=∠2,∠3=80°,则∠4等于
( )
A.
80°
B.
70°
C.
60°
D.
50°
5、下列图中和是同位角的是
(
)
A.
①②③
B.
②③④
C.
①②④
D.
①②
6、如图,由∠1=∠2,则可得出( )
AB∥CD
B.
AD∥BC
C.
A
D∥BC
且
AB∥CD
D.
∠3=∠4
7、如图,已知a∥b,直角三角板的直角顶点在直线a上,若∠1=30°,则∠2等于(
)
A.
30°
B.
40°
C.
50°
D.
60°
8、如图,不能判定AB∥CD的条件是(
)
A.
∠B+∠BCD=180°
B.
∠1=∠2
C.
∠3=∠4
D.
∠B=∠5
9、如图,将一块含的三角板叠放在直尺上,若,则( )
A.
B.
C.
D.
10、如图
可以得到(
)
B.
C.
D.
填空。
11、如图,已知DE∥BC,∠ABC=40°,则∠ADE=________.
12、如图,直线EF分别交AB、CD于点E、F,EG平分∠BEF,AB∥CD.若∠1=74°,则∠2
的度数为______度.
13、如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为__________.(任意添加一个符合题意的条件即可)
如图,
∠1
和∠4
是
.
15、如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为_______.
解答。
16、完成下列推理说明:如图,已知∠A=∠F,∠C=∠D,试说明:BD∥CE.
∵∠A=∠F(?已知?),
∴___∥___(
),
∴___=∠1(
),
又∵∠C=∠D(?已知?),
∴∠1=___(
),
∴BD∥CE(
).
17、阅读理解,补全证明过程及推理依据.
已知:如图,点E在直线DF上,点B在直线AC上,∠1=∠2,∠3=∠4.
求证∠A=∠F
证明:∵∠1=∠2(已知)
∠2=∠DGF(
)
∴∠1=∠DGF(等量代换)
∴
∥
(
)
∴∠3+∠
=180°(
)
又∵∠3=∠4(已知)
∴∠4+∠C=180°(等量代换)
∴
∥
(
)
∴∠A=∠F(
)
18、如图,∠1=70°,∠2=110°,∠C=∠D,试探索∠A与∠F有怎样的数量关系,并说明理由.
答案
C
2、C
3、C
4、A
5、D
A
7、D
8、B
9、D
10、B
11、40°
12、53°
13、∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE
14、同位角
15、56°
16、内错角相等,两直线平行;∠1;两直线平行,内错角相等;∠C;等量代换;同位角相等,两直线平行
17、对顶角相等;BD;CE;同位角相等,两直线平行;C;两直线平行,同旁内角互补;AC,DF;同旁内角互补,两直线平行;两直线平行,内错角相等.
18、∠A=∠F.
理由如下:
∵∠1=70°,∠2=110°,∴∠1+∠2=180°,∴CE∥DB,∴∠C=∠ABD.∵∠C=∠D,∴∠ABD=∠D,∴AC∥DF,∴∠A=∠F.
1、下列说法正确的有(
)
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个
B.2个
C.3个
D.4个
2、下列图形中,表示∠1和∠2是对顶角的图形是(
)
3、如图所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于(
)
A.150°
B.180°
C.210°
D.120°
4、如图,三条直线,,相交于点,则( )
A.
B.
C.
D.
5、直线AB、CD交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于(
)
A、38°
B、104°
C、142°
D、144°
6、下列语句错误的有(
)个.
(1)两个角的两边分别在同一条直线上,这两个角互为对顶角
(2)有公共顶点并且相等的两个角是对顶角
(3)如果两个角相等,那么这两个角互补
(4)如果两个角不相等,那么这两个角不是对顶角
A.1
B.2
C.3
D.4
7、如图,平面上三条不同的直线相交最多能构成对顶角的对数是(
)
A.4
B.5
C.6
D.7
7、如图,AB∥CD,AC⊥BC,∠BAC=65°,则∠BCD=______________度。
8、如图所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.
9、如图,当剪子口∠AOB增大15°时,∠COD增大____________。
10、已知∠1与∠2是对顶角,∠1与∠3互为补角,则∠2+∠3=
。
11、如图,直线a,b,c两两相交,∠1=2∠3,∠2=68°,求∠4的度数.
12、如图所示,直线AB与CD相交于点O,∠AOC:∠AOD=2:3,求∠BOD的度数.
13、如图,∠1=∠2,∠1+∠2=162°,求∠3与∠4的度数。
14、如图,O为直线AB上一点,∠BOC
=
3∠AOC,OC平分∠AOD;
⑴
求∠AOC的度数;
⑵
推测OD与AB的位置关系,并说明理由。
15、如图,直线a,b,c两两相交,∠1=2∠3,∠2=68°,求∠4的度数.
5.1.2垂线
选择。
1、与一条已知直线垂直的直线有(
)
A.
1条
B.
2条
C.
3条
D.
无数条
2、下列图形中线段PQ的长度表示点P到直线a的距离的是( )
A.
B.
C.
D.
3、如图,是一条河流,要铺设管道将河水引到两个用水点和,现有两种铺设管道的方案;
方案一:分别过、作的垂线,垂足为、,沿、铺设管道;
方案二:连接交于点,沿,铺设管道.
下列说法正确的是(
)
A.
方案一比方案二省钱,因为垂线段最短
B.
方案二比方案一省钱,因为两点之间,线段最短
C.
方案一与方案二一样省钱,因为管道长度一样
D.
方案一与方案二都不是最省钱的方案
4、1.如图,体育课上测量跳远成绩的依据是(
)
A.平行线间的距离相等
B.两点之间,线段最短
C.垂线段最短
D.两点确定一条直线
5、如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
A.两点之间线段最短
B.点到直线的距离
C.两点确定一条直线
D.垂线段最短
6、在下列生活实例中,数学依据不正确的是(
)
A.在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上,依据的是两点确定一条直线;
B.在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标,依据的是两点之间线段最短;
C.从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,大大节约了路程,依据的是两点之间线段最短;
D.体育课上,体育老师测量跳远距离的时候,测的是落脚脚跟到起跳线的距离,依据的是垂线段最短.
7、体育课上,老师测量跳远成绩的依据是(
)
A.两点确定一条直线
B.两点之间,线段最短
C.垂线段最短
D.平行线间的距离相等
8、如图,点P是直线a外一点,PB⊥a,点A,B,C,D都在直线a上,下列线段中最短的是(
)
A.PA
B.PB
C.PC
D.PD
填空。
9、连接直线外一点与直线上各点的所有线段中,__________最短.
10、如图所示,想在河堤两岸塔建一座桥,搭建方式最短的是_____,理由_____.
11、如图,从D处开渠引水到C处,则渠道CD最短,依据是__________.
12、定点P在直线AB外,动点O在直线AB上移动,当PO最短时,∠POA=_______.这时线段PO所在的直线是直线AB的________,线段PO叫做直线AB的__________.
解答。
如图,要从小河a引水到村庄A,请设计并作出一最短路线,画在图中。
14、如图,AC⊥CD,∠BED=90°.填空:
(1)∠ACD=_____度;
(2)直线AD与BE的位置关系是__________;
(3)点B到直线AD的距离是线段________的长度,点D到直线AB的距离是线段______的长度;
(4)在线段DA,DB,DC中,最短的是线段______;在线段BA,BE,BD中,最短的是线段______,理由是_____________________________________.
15、已知:四点A,B,C,D的位置如图所示,
(1)连接AD;
(2)画射线AB与线段DC的延长线交于点E;
(3)过点B作BF⊥CD于点F.
16、如图,AD⊥BC于点D,EF⊥BC于点F,∠BDG=∠C.试说明∠1=∠2.
17、如图,直线、相交于点,,与的度数之比为.求的度数.
18、(1)如图1,村庄A到公路BC的最短距离是AD,根据是________.
(2)如图2,建筑工人常在一根细绳上拴上一个重物,做成一个“铅锤”,挂铅锤的线总垂直于地面内的任何直线,当这条线贴近墙壁时,说明墙与地面垂直,请说出它的根据是____________________________.
答案
D
2、C
3、A
4、C
D
6、B
7、C
8、B
垂线段
PN,
垂线段最短
垂线段最短
90°
垂线
垂线段
(1)
90
;(2)
互相垂直
;(3)
BE,DC
;(4)
DC,
BE,连结直线外一点与直线上各点的所有线段中,垂线段最短
如图:(1)连接AD,
(2)作射线AB,线段DC,并延长线段DC交于射线AB与E,
(3)过点B作BF⊥CD于点F.
16、∵AD⊥BC于点D,EF⊥BC于点F,∴∠ADB=∠FEC=90°.
∵∠BDG=∠C,∠2+∠BDG=90°,∠1+∠C=90°,∴∠1=∠2.
17、度数为.
18、(1)垂线段最短;
(2)过一点有且只有一条直线与已知直线垂直
5.1.3同位角、内错角、同旁内角
选择。
1、如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.
如果∠1=20°,那么∠2的度数是(
)
A.15°
B.20°
C.25°
D.30°
2、如图,点E在BC的延长线上,下列条件不能判定AB∥CD的是(
)
∠3=∠4
B.
∠B=∠DCE
C.
∠4=∠2
D.
∠D+∠DAB=180°
3、
如图,直线a,b被直线c所截,a∥b,若∠2=45°,则∠1等于( )
A.
125°
B.
130°
C.
135°
D.
145°
4、如图,∠1=∠2,∠3=80°,则∠4等于
( )
A.
80°
B.
70°
C.
60°
D.
50°
5、下列图中和是同位角的是
(
)
A.
①②③
B.
②③④
C.
①②④
D.
①②
6、如图,由∠1=∠2,则可得出( )
AB∥CD
B.
AD∥BC
C.
A
D∥BC
且
AB∥CD
D.
∠3=∠4
7、如图,已知a∥b,直角三角板的直角顶点在直线a上,若∠1=30°,则∠2等于(
)
A.
30°
B.
40°
C.
50°
D.
60°
8、如图,不能判定AB∥CD的条件是(
)
A.
∠B+∠BCD=180°
B.
∠1=∠2
C.
∠3=∠4
D.
∠B=∠5
9、如图,将一块含的三角板叠放在直尺上,若,则( )
A.
B.
C.
D.
10、如图
可以得到(
)
B.
C.
D.
填空。
11、如图,已知DE∥BC,∠ABC=40°,则∠ADE=________.
12、如图,直线EF分别交AB、CD于点E、F,EG平分∠BEF,AB∥CD.若∠1=74°,则∠2
的度数为______度.
13、如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为__________.(任意添加一个符合题意的条件即可)
如图,
∠1
和∠4
是
.
15、如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为_______.
解答。
16、完成下列推理说明:如图,已知∠A=∠F,∠C=∠D,试说明:BD∥CE.
∵∠A=∠F(?已知?),
∴___∥___(
),
∴___=∠1(
),
又∵∠C=∠D(?已知?),
∴∠1=___(
),
∴BD∥CE(
).
17、阅读理解,补全证明过程及推理依据.
已知:如图,点E在直线DF上,点B在直线AC上,∠1=∠2,∠3=∠4.
求证∠A=∠F
证明:∵∠1=∠2(已知)
∠2=∠DGF(
)
∴∠1=∠DGF(等量代换)
∴
∥
(
)
∴∠3+∠
=180°(
)
又∵∠3=∠4(已知)
∴∠4+∠C=180°(等量代换)
∴
∥
(
)
∴∠A=∠F(
)
18、如图,∠1=70°,∠2=110°,∠C=∠D,试探索∠A与∠F有怎样的数量关系,并说明理由.
答案
C
2、C
3、C
4、A
5、D
A
7、D
8、B
9、D
10、B
11、40°
12、53°
13、∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE
14、同位角
15、56°
16、内错角相等,两直线平行;∠1;两直线平行,内错角相等;∠C;等量代换;同位角相等,两直线平行
17、对顶角相等;BD;CE;同位角相等,两直线平行;C;两直线平行,同旁内角互补;AC,DF;同旁内角互补,两直线平行;两直线平行,内错角相等.
18、∠A=∠F.
理由如下:
∵∠1=70°,∠2=110°,∴∠1+∠2=180°,∴CE∥DB,∴∠C=∠ABD.∵∠C=∠D,∴∠ABD=∠D,∴AC∥DF,∴∠A=∠F.
