2.2 探索直线平行的条件(1)三线八角同步练习(含解析)
文档属性
| 名称 | 2.2 探索直线平行的条件(1)三线八角同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 00:00:00 | ||
图片预览




文档简介
2.3探索直线平行的条件(1)三线八角
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020秋?香坊区期末)如图,∠1和∠2不是同旁内角的是( )
A. B.
C. D.
2.(2020秋?长春期末)如图,∠B的内错角是( )
A.∠1 B.∠2 C.∠3 D.∠4
3.(2020秋?朝阳区期末)如图,直线b、c被直线a所截,则∠1与∠2是( )
A.内错角 B.同位角 C.同旁内角 D.对顶角
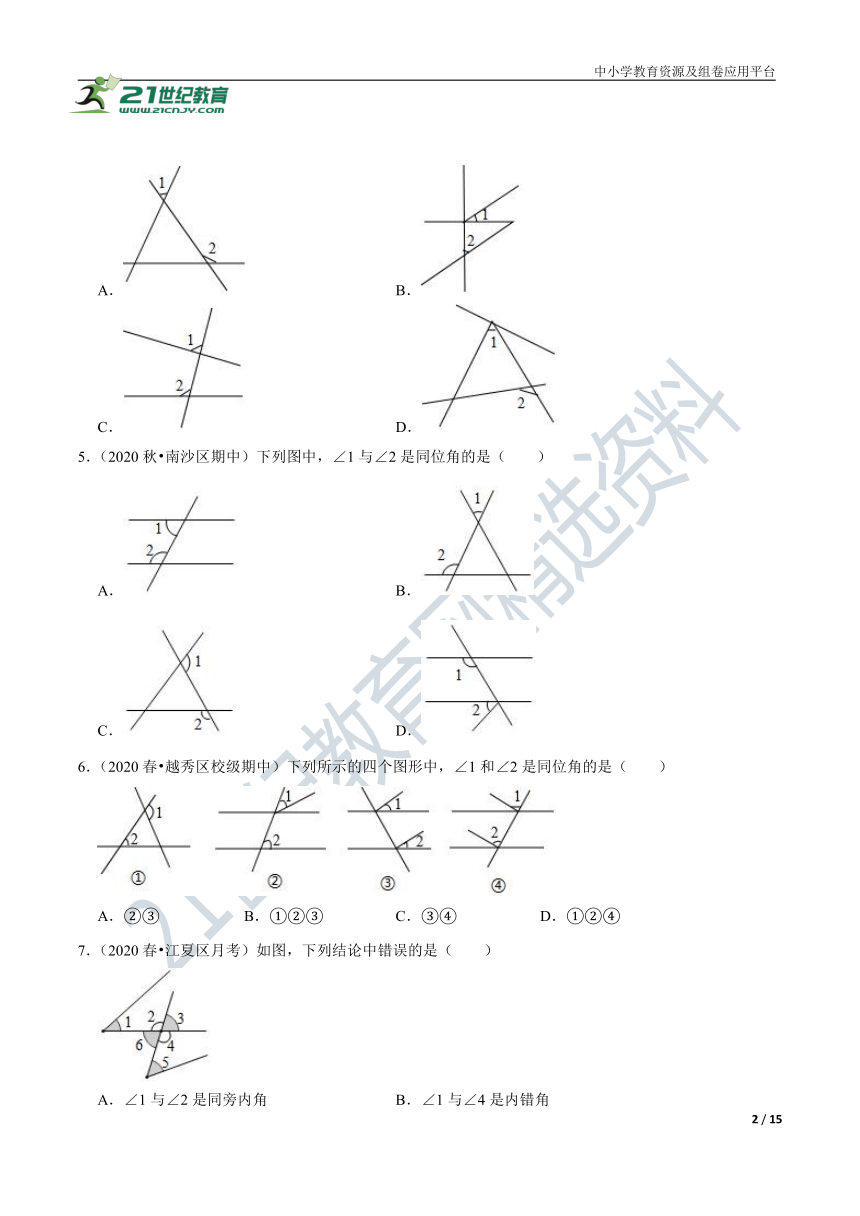
4.(2020秋?淅川县期末)如图图形中,∠1和∠2不是同位角的是( )
A. B.
C. D.
5.(2020秋?南沙区期中)下列图中,∠1与∠2是同位角的是( )
A. B.
C. D.
6.(2020春?越秀区校级期中)下列所示的四个图形中,∠1和∠2是同位角的是( )
A.②③ B.①②③ C.③④ D.①②④
7.(2020春?江夏区月考)如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角 B.∠1与∠4是内错角
C.∠5与∠6是内错角 D.∠3与∠5是同位角
8.(2020春?舞钢市期末)如图,给出以下说法:①∠B和∠1是同旁内角;②∠3和∠4是内错角;③∠B和∠AEC是同位角;④∠A和∠3是内错角;⑤∠2和∠3是对顶角,其中正确的个数是( )
A.4个 B.3个 C.2个 D.1个
9.(2020春?莘县期末)如图所示,下列说法:
①∠1与∠C是同位角;
②∠2与∠C是内错角;
③∠3与∠B是同旁内角;
④∠3与∠C是同旁内角.
其中正确的是( )
A.①②③ B.②③④ C.①③④ D.①②④
10.(2020春?民权县期末)如图,给出下列说法:①∠A和∠4是同位角;②∠1和∠3是对顶角;③∠2和∠4是内错角;④∠A和∠BCD是同旁内角.其中说法错误的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020春?和平区期中)如图,同旁内角有 对.
12.(2020春?公主岭市期中)如图,直线AB,CD被直线EF所截,如果∠2=100°,那么∠1的同位角等于 度.
13.(2019秋?卧龙区期末)如图,下列结论:①∠2与∠3是内错角;②∠2与∠B是同位角;③∠A与∠B是同旁内角;④∠A与∠ACB不是同旁内角,其中正确的是 (只填序号).
14.(2020春?麻城市校级月考)如图,∠1和∠3是直线 和 被直线 所截而成的 角;图中与∠2是同旁内角的角有 个.
15.(2020春?高州市期中)如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于 ,∠3的内错角等于 ,∠3的同旁内角等于 .
16.(2020秋?杨浦区校级期中)如图,共有 对同位角,有 对内错角,有 对同旁内角.
17.(2019春?云梦县期中)如图,有下列判断:
①∠A与∠1是同位角;
②∠A与∠B是同旁内角;
③∠4与∠C是内错角;
④∠2与∠3是对顶角.其中正确的是 (填序号).
18.(2020春?西湖区期末)如图,有下列3个结论:①能与∠DEF构成内错角的角的个数是2;②能与∠EFB构成同位角的角的个数是1;③能与∠C构成同旁内角的角的个数是4,以上结论正确的是 .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2019春?琼中县期中)如图所示,找出图中的同位角、内错角、同旁内角(仅限于用数字表示).
20.(2020春?澧县期末)分别指出下列图中的同位角、内错角、同旁内角.
21.(2019春?长春月考)根据图形填空:
(1)若直线ED、BC被直线AB所截,则∠1和 是同位角;
(2)若直线ED、BC被直线AF所截,则∠3和 是内错角;
(3)∠1和∠3是直线AB、AF被直线 所截构成的内错角.
(4)∠2和∠4是直线AB、 被直线BC所截构成的 角.
22.(2019秋?崇川区校级期末)复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线l1,l2被直线l3所截,在这个基本图形中,形成了 对同旁内角.
(2)如图2,平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有 对同旁内角.
(3)平面内四条直线两两相交,最多可以形成 对同旁内角.
(4)平面内n条直线两两相交,最多可以形成 对同旁内角.
23.(2020春?大悟县期中)如图,直线DE经过点A.
(1)写出∠B的内错角是 ,同旁内角是 .
(2)若∠EAC=∠C,AC平分∠BAE,∠B=44°,求∠C的度数.
24.(2019?上城区一模)两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3.
(2)若∠1=2∠2,∠2=2∠3,求∠3的度数.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】选项A、B、C中,∠1与∠2在两直线的之间,并且在第三条直线(截线)的同旁,是同旁内角;
选项D中,∠1与∠2的两条边都不在同一条直线上,不是同旁内角.
故选:D.
2.【解析】A、∠B的内错角是∠1,故此选项符合题意;
B、∠B与∠2是同旁内角,故此选项不合题意;
C、∠B与∠3是同位角,故此选项不合题意;
D、∠B与∠4是不是内错角,故此选项不合题意;
故选:A.
3.【解析】直线b、c被直线a所截,则∠1与∠2是同位角,
故选:B.
4.【解析】∵选项B中∠1和∠2是由四条直线组成,
∴∠1和∠2不是同位角.
故选:B.
5.【解析】选项A中的两个角是同旁内角,因此不符合题意;
选项C中的两个角既不是同位角、也不是内错角、同旁内角,因此不符合题意;
选项D不是两条直线被一条直线所截出现的角,不符合题意;
只有选项B中的两个角符合同位角的意义,符合题意;
故选:B.
6.【解析】图①②④中,∠1和∠2是同位角,
故选:D.
7.【解析】如图,∠1与∠2是直线a与直线b被直线c所截的同旁内角,因此选项A不符合题意;
∠1与∠6是直线a与直线b被直线c所截的内错角,而∠6与∠4是邻补角,所以∠1与∠4不是内错角,因此选项B符合题意;
∠5与∠6是直线c与直线d被直线b所截的内错角,因此选项C不符合题意;
∠3与∠5是直线c与直线d被直线b所截的同位角,因此选项D不符合题意;
故选:B.
8.【解析】∠B和∠1是直线AB和CE被直线BC所截的一对同旁内角,故①正确;
∠3和∠4不是内错角,故②错误;
∠B和∠AEC是直线CE和BC被直线AB所截的一对同位角,故③正确;
∠A和∠3是直线AB和CD被直线AC所截的一对内错角,故④正确;
∠2和∠3不是对顶角,故⑤错误;
即正确的有3个,
故选:B.
9.【解析】①∠1与∠C是同位角,说法正确;
②∠2与∠C是内错角,说法错误;
③∠3与∠B是同旁内角,说法正确;
④∠3与∠C是同旁内角,说法正确;
故选:C.
10.【解析】①∠A和∠4是同位角,说法正确;
②∠1和∠3是对顶角,说法错误;
③∠2和∠4是内错角,说法正确;
④∠A和∠BCD是同旁内角说法错误;
说法错误的有2个,
故选:B.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】∠1和∠2,∠1和∠6,∠2和∠6,∠3和∠7是同旁内角,
共4对,
故答案为:4.
12.【解析】∵∠2=100°,
∴∠3=180°﹣100°=80°,
∴∠1的同位角∠3为80°,
故答案为:80.
13.【解析】∠2与∠3是直线AB、直线BC,被直线CD所截的一对内错角,因此①符合题意;
∠2与∠B是直线CD、直线BC,被直线AB所截的一对同位角,因此②符合题意;
∠A与∠B是直线AC、直线BC,被直线AB所截的一对同旁内角,因此③符合题意,
∠A与∠ACB是直线AB、直线BC,被直线AC所截的一对同旁内角,因此④不符合题意,
故答案为:①②③.
14.【解析】∠1和∠3是直线AB和AC被直线DE所截而成的内错角;图中与∠2 是同旁内角的角有∠6、∠5、∠7,共3个,
故答案为:AB、AC、DE、内错,3.
15.【解析】如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于80°,∠3的内错角等于80°,∠3的同旁内角等于100°,
故答案为:80°;80°;100°
16.【解析】同位角:∠AEO和∠CGE,∠OEF和∠EGH,∠OFB和∠OHD,∠OFE和∠OHG,∠IGH和∠IEF,∠AEI和∠CGI,∠AFJ和∠CHJ,∠DHJ和∠JFB,∠AEO和∠AFO,∠OEB和∠OFB,∠AEG和∠AFH,∠GEB和∠HFB,∠EGH和∠OHD,∠OGC和∠OHC,∠O与∠EFH,∠O与∠GEF,∠O和∠IGH,∠O和∠GHJ,
∠CGI和∠CHJ,∠HGI和∠DHJ,共20对;
内错角:∠O和∠OEA,∠O和∠OFB,∠O和∠OGC,∠O和∠OHD,∠AEG和∠EGH,∠BEG和∠EGC,∠BFH和∠FHC,∠AFH和∠FHD,∠OEF和∠EFH,∠GEF和∠OFE,∠OGH和∠GHJ,∠OHG和∠IGH,共12对;
同旁内角:∠OEF和∠O,∠OFE和∠O,∠O和∠OGH,∠O和∠OHC,∠OEF和∠OFE,∠OGH和∠OHG,∠GEF和∠EFH,∠IGH和∠GHJ,∠AEG和∠CGE,∠BFH和∠FHD,∠FEG和∠EGH,∠EFH和∠GHF,共12对,
故答案为:20;12;12.
17.【解析】①∠A与∠1是同位角,说法正确;
②∠A与∠B是同旁内角,说法正确;
③∠4与∠C是内错角,说法错误,应为同旁内角;
④∠2与∠3是对顶角,说法正确,
正确的说法有①②④,
故答案为:①②④.
18.【解析】①能与∠DEF构成内错角的角的个数有2个,即∠EFA和∠EDC,故正确;
②能与∠EFB构成同位角的角的个数只有1个:即∠FAE,故正确;
③能与∠C构成同旁内角的角的个数有5个:即∠CDE,∠B,∠CED,∠CEF,∠A,故错误;
所以结论正确的是①②.
故答案为:①②.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】由图可得:
同位角:∠1与∠3,∠3与∠5;
内错角:∠1与∠4,∠4与∠5;
同旁内角:∠1与∠2,∠6与∠5.
20.【解析】如图1,
同位角有:∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8;
内错角有:∠3与∠6,∠4与∠5;
同旁内角有:∠3与∠5,∠4与∠6.
如图2,
同位角有:∠1与∠3,∠2与∠4;
同旁内角有:∠3与∠2.
21.【解析】(1)如图:若ED,BC被AB所截,则∠1与∠2是同位角,
(2)若ED,BC被AF所截,则∠3与∠4是内错角,
(3)∠1 与∠3是AB和AF被ED所截构成的内错角,
(4)∠2与∠4是AB和AF被BC所截构成的同位角.
故答案是:(1)∠2.(2)∠4.(3)ED.(4)AF;同位.
22.【解析】(1)直线l1,l2被直线l3所截,在这个基本图形中,形成了2对同旁内角.
(2)平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有6对同旁内角.
(3)平面内四条直线两两相交,最多可以形成24对同旁内角.
(4)平面内n条直线两两相交,最多可以形成n(n﹣1)(n﹣2)对同旁内角
故答案为:(1)2;(2)6;(3)24;(4)n(n﹣1)(n﹣2)
23.【解析】(1)∠B的内错角是∠BAD,∠B的同旁内角是∠BAC,∠EAB和∠C;
(2)∵∠EAC=∠C,
∴DE∥BC,
∴∠BAE=180°﹣44°=136°,
∵AC平分∠BAE,
∴∠EAC=68°,
∴∠C=∠EAC=68°,
故答案为:∠BAD;∠BAC,∠EAB和∠C
24.【解析】(1)如图所示:
(2)∵∠1=2∠2,∠2=2∠3,
∴设∠3=x,则∠2=2x,∠1=4x,
∵∠1+∠3=180°,
∴x+4x=180°,
解得:x=36°,
故∠3=36°.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020秋?香坊区期末)如图,∠1和∠2不是同旁内角的是( )
A. B.
C. D.
2.(2020秋?长春期末)如图,∠B的内错角是( )
A.∠1 B.∠2 C.∠3 D.∠4
3.(2020秋?朝阳区期末)如图,直线b、c被直线a所截,则∠1与∠2是( )
A.内错角 B.同位角 C.同旁内角 D.对顶角
4.(2020秋?淅川县期末)如图图形中,∠1和∠2不是同位角的是( )
A. B.
C. D.
5.(2020秋?南沙区期中)下列图中,∠1与∠2是同位角的是( )
A. B.
C. D.
6.(2020春?越秀区校级期中)下列所示的四个图形中,∠1和∠2是同位角的是( )
A.②③ B.①②③ C.③④ D.①②④
7.(2020春?江夏区月考)如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角 B.∠1与∠4是内错角
C.∠5与∠6是内错角 D.∠3与∠5是同位角
8.(2020春?舞钢市期末)如图,给出以下说法:①∠B和∠1是同旁内角;②∠3和∠4是内错角;③∠B和∠AEC是同位角;④∠A和∠3是内错角;⑤∠2和∠3是对顶角,其中正确的个数是( )
A.4个 B.3个 C.2个 D.1个
9.(2020春?莘县期末)如图所示,下列说法:
①∠1与∠C是同位角;
②∠2与∠C是内错角;
③∠3与∠B是同旁内角;
④∠3与∠C是同旁内角.
其中正确的是( )
A.①②③ B.②③④ C.①③④ D.①②④
10.(2020春?民权县期末)如图,给出下列说法:①∠A和∠4是同位角;②∠1和∠3是对顶角;③∠2和∠4是内错角;④∠A和∠BCD是同旁内角.其中说法错误的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020春?和平区期中)如图,同旁内角有 对.
12.(2020春?公主岭市期中)如图,直线AB,CD被直线EF所截,如果∠2=100°,那么∠1的同位角等于 度.
13.(2019秋?卧龙区期末)如图,下列结论:①∠2与∠3是内错角;②∠2与∠B是同位角;③∠A与∠B是同旁内角;④∠A与∠ACB不是同旁内角,其中正确的是 (只填序号).
14.(2020春?麻城市校级月考)如图,∠1和∠3是直线 和 被直线 所截而成的 角;图中与∠2是同旁内角的角有 个.
15.(2020春?高州市期中)如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于 ,∠3的内错角等于 ,∠3的同旁内角等于 .
16.(2020秋?杨浦区校级期中)如图,共有 对同位角,有 对内错角,有 对同旁内角.
17.(2019春?云梦县期中)如图,有下列判断:
①∠A与∠1是同位角;
②∠A与∠B是同旁内角;
③∠4与∠C是内错角;
④∠2与∠3是对顶角.其中正确的是 (填序号).
18.(2020春?西湖区期末)如图,有下列3个结论:①能与∠DEF构成内错角的角的个数是2;②能与∠EFB构成同位角的角的个数是1;③能与∠C构成同旁内角的角的个数是4,以上结论正确的是 .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2019春?琼中县期中)如图所示,找出图中的同位角、内错角、同旁内角(仅限于用数字表示).
20.(2020春?澧县期末)分别指出下列图中的同位角、内错角、同旁内角.
21.(2019春?长春月考)根据图形填空:
(1)若直线ED、BC被直线AB所截,则∠1和 是同位角;
(2)若直线ED、BC被直线AF所截,则∠3和 是内错角;
(3)∠1和∠3是直线AB、AF被直线 所截构成的内错角.
(4)∠2和∠4是直线AB、 被直线BC所截构成的 角.
22.(2019秋?崇川区校级期末)复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线l1,l2被直线l3所截,在这个基本图形中,形成了 对同旁内角.
(2)如图2,平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有 对同旁内角.
(3)平面内四条直线两两相交,最多可以形成 对同旁内角.
(4)平面内n条直线两两相交,最多可以形成 对同旁内角.
23.(2020春?大悟县期中)如图,直线DE经过点A.
(1)写出∠B的内错角是 ,同旁内角是 .
(2)若∠EAC=∠C,AC平分∠BAE,∠B=44°,求∠C的度数.
24.(2019?上城区一模)两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3.
(2)若∠1=2∠2,∠2=2∠3,求∠3的度数.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】选项A、B、C中,∠1与∠2在两直线的之间,并且在第三条直线(截线)的同旁,是同旁内角;
选项D中,∠1与∠2的两条边都不在同一条直线上,不是同旁内角.
故选:D.
2.【解析】A、∠B的内错角是∠1,故此选项符合题意;
B、∠B与∠2是同旁内角,故此选项不合题意;
C、∠B与∠3是同位角,故此选项不合题意;
D、∠B与∠4是不是内错角,故此选项不合题意;
故选:A.
3.【解析】直线b、c被直线a所截,则∠1与∠2是同位角,
故选:B.
4.【解析】∵选项B中∠1和∠2是由四条直线组成,
∴∠1和∠2不是同位角.
故选:B.
5.【解析】选项A中的两个角是同旁内角,因此不符合题意;
选项C中的两个角既不是同位角、也不是内错角、同旁内角,因此不符合题意;
选项D不是两条直线被一条直线所截出现的角,不符合题意;
只有选项B中的两个角符合同位角的意义,符合题意;
故选:B.
6.【解析】图①②④中,∠1和∠2是同位角,
故选:D.
7.【解析】如图,∠1与∠2是直线a与直线b被直线c所截的同旁内角,因此选项A不符合题意;
∠1与∠6是直线a与直线b被直线c所截的内错角,而∠6与∠4是邻补角,所以∠1与∠4不是内错角,因此选项B符合题意;
∠5与∠6是直线c与直线d被直线b所截的内错角,因此选项C不符合题意;
∠3与∠5是直线c与直线d被直线b所截的同位角,因此选项D不符合题意;
故选:B.
8.【解析】∠B和∠1是直线AB和CE被直线BC所截的一对同旁内角,故①正确;
∠3和∠4不是内错角,故②错误;
∠B和∠AEC是直线CE和BC被直线AB所截的一对同位角,故③正确;
∠A和∠3是直线AB和CD被直线AC所截的一对内错角,故④正确;
∠2和∠3不是对顶角,故⑤错误;
即正确的有3个,
故选:B.
9.【解析】①∠1与∠C是同位角,说法正确;
②∠2与∠C是内错角,说法错误;
③∠3与∠B是同旁内角,说法正确;
④∠3与∠C是同旁内角,说法正确;
故选:C.
10.【解析】①∠A和∠4是同位角,说法正确;
②∠1和∠3是对顶角,说法错误;
③∠2和∠4是内错角,说法正确;
④∠A和∠BCD是同旁内角说法错误;
说法错误的有2个,
故选:B.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】∠1和∠2,∠1和∠6,∠2和∠6,∠3和∠7是同旁内角,
共4对,
故答案为:4.
12.【解析】∵∠2=100°,
∴∠3=180°﹣100°=80°,
∴∠1的同位角∠3为80°,
故答案为:80.
13.【解析】∠2与∠3是直线AB、直线BC,被直线CD所截的一对内错角,因此①符合题意;
∠2与∠B是直线CD、直线BC,被直线AB所截的一对同位角,因此②符合题意;
∠A与∠B是直线AC、直线BC,被直线AB所截的一对同旁内角,因此③符合题意,
∠A与∠ACB是直线AB、直线BC,被直线AC所截的一对同旁内角,因此④不符合题意,
故答案为:①②③.
14.【解析】∠1和∠3是直线AB和AC被直线DE所截而成的内错角;图中与∠2 是同旁内角的角有∠6、∠5、∠7,共3个,
故答案为:AB、AC、DE、内错,3.
15.【解析】如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于80°,∠3的内错角等于80°,∠3的同旁内角等于100°,
故答案为:80°;80°;100°
16.【解析】同位角:∠AEO和∠CGE,∠OEF和∠EGH,∠OFB和∠OHD,∠OFE和∠OHG,∠IGH和∠IEF,∠AEI和∠CGI,∠AFJ和∠CHJ,∠DHJ和∠JFB,∠AEO和∠AFO,∠OEB和∠OFB,∠AEG和∠AFH,∠GEB和∠HFB,∠EGH和∠OHD,∠OGC和∠OHC,∠O与∠EFH,∠O与∠GEF,∠O和∠IGH,∠O和∠GHJ,
∠CGI和∠CHJ,∠HGI和∠DHJ,共20对;
内错角:∠O和∠OEA,∠O和∠OFB,∠O和∠OGC,∠O和∠OHD,∠AEG和∠EGH,∠BEG和∠EGC,∠BFH和∠FHC,∠AFH和∠FHD,∠OEF和∠EFH,∠GEF和∠OFE,∠OGH和∠GHJ,∠OHG和∠IGH,共12对;
同旁内角:∠OEF和∠O,∠OFE和∠O,∠O和∠OGH,∠O和∠OHC,∠OEF和∠OFE,∠OGH和∠OHG,∠GEF和∠EFH,∠IGH和∠GHJ,∠AEG和∠CGE,∠BFH和∠FHD,∠FEG和∠EGH,∠EFH和∠GHF,共12对,
故答案为:20;12;12.
17.【解析】①∠A与∠1是同位角,说法正确;
②∠A与∠B是同旁内角,说法正确;
③∠4与∠C是内错角,说法错误,应为同旁内角;
④∠2与∠3是对顶角,说法正确,
正确的说法有①②④,
故答案为:①②④.
18.【解析】①能与∠DEF构成内错角的角的个数有2个,即∠EFA和∠EDC,故正确;
②能与∠EFB构成同位角的角的个数只有1个:即∠FAE,故正确;
③能与∠C构成同旁内角的角的个数有5个:即∠CDE,∠B,∠CED,∠CEF,∠A,故错误;
所以结论正确的是①②.
故答案为:①②.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】由图可得:
同位角:∠1与∠3,∠3与∠5;
内错角:∠1与∠4,∠4与∠5;
同旁内角:∠1与∠2,∠6与∠5.
20.【解析】如图1,
同位角有:∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8;
内错角有:∠3与∠6,∠4与∠5;
同旁内角有:∠3与∠5,∠4与∠6.
如图2,
同位角有:∠1与∠3,∠2与∠4;
同旁内角有:∠3与∠2.
21.【解析】(1)如图:若ED,BC被AB所截,则∠1与∠2是同位角,
(2)若ED,BC被AF所截,则∠3与∠4是内错角,
(3)∠1 与∠3是AB和AF被ED所截构成的内错角,
(4)∠2与∠4是AB和AF被BC所截构成的同位角.
故答案是:(1)∠2.(2)∠4.(3)ED.(4)AF;同位.
22.【解析】(1)直线l1,l2被直线l3所截,在这个基本图形中,形成了2对同旁内角.
(2)平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有6对同旁内角.
(3)平面内四条直线两两相交,最多可以形成24对同旁内角.
(4)平面内n条直线两两相交,最多可以形成n(n﹣1)(n﹣2)对同旁内角
故答案为:(1)2;(2)6;(3)24;(4)n(n﹣1)(n﹣2)
23.【解析】(1)∠B的内错角是∠BAD,∠B的同旁内角是∠BAC,∠EAB和∠C;
(2)∵∠EAC=∠C,
∴DE∥BC,
∴∠BAE=180°﹣44°=136°,
∵AC平分∠BAE,
∴∠EAC=68°,
∴∠C=∠EAC=68°,
故答案为:∠BAD;∠BAC,∠EAB和∠C
24.【解析】(1)如图所示:
(2)∵∠1=2∠2,∠2=2∠3,
∴设∠3=x,则∠2=2x,∠1=4x,
∵∠1+∠3=180°,
∴x+4x=180°,
解得:x=36°,
故∠3=36°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
