2.3.2 平行线的性质与判定(培优)同步练习(含解析)
文档属性
| 名称 | 2.3.2 平行线的性质与判定(培优)同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 13:28:19 | ||
图片预览




文档简介
2.7平行线的性质与判定(培优)
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一.解答题(共20小题)
1.(2020秋?长春期末)如图,∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
在下列解答中,填空:
证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE( ).
∴∠ABC=∠BCD( ).
∵∠P=∠Q(已知),
∴PB∥( )( ).
∴∠PBC=( )(两直线平行,内错角相等).
∵∠1=∠ABC﹣( ),∠2=∠BCD﹣( ),
∴∠1=∠2(等量代换).
2.(2020秋?松北区期末)完成下面的证明:
如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
证明:∵DE∥AB(已知),
∴∠A=∠CED( )
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD( )
∴DF∥AE( )
∴∠EGF+∠AEG=180°( )
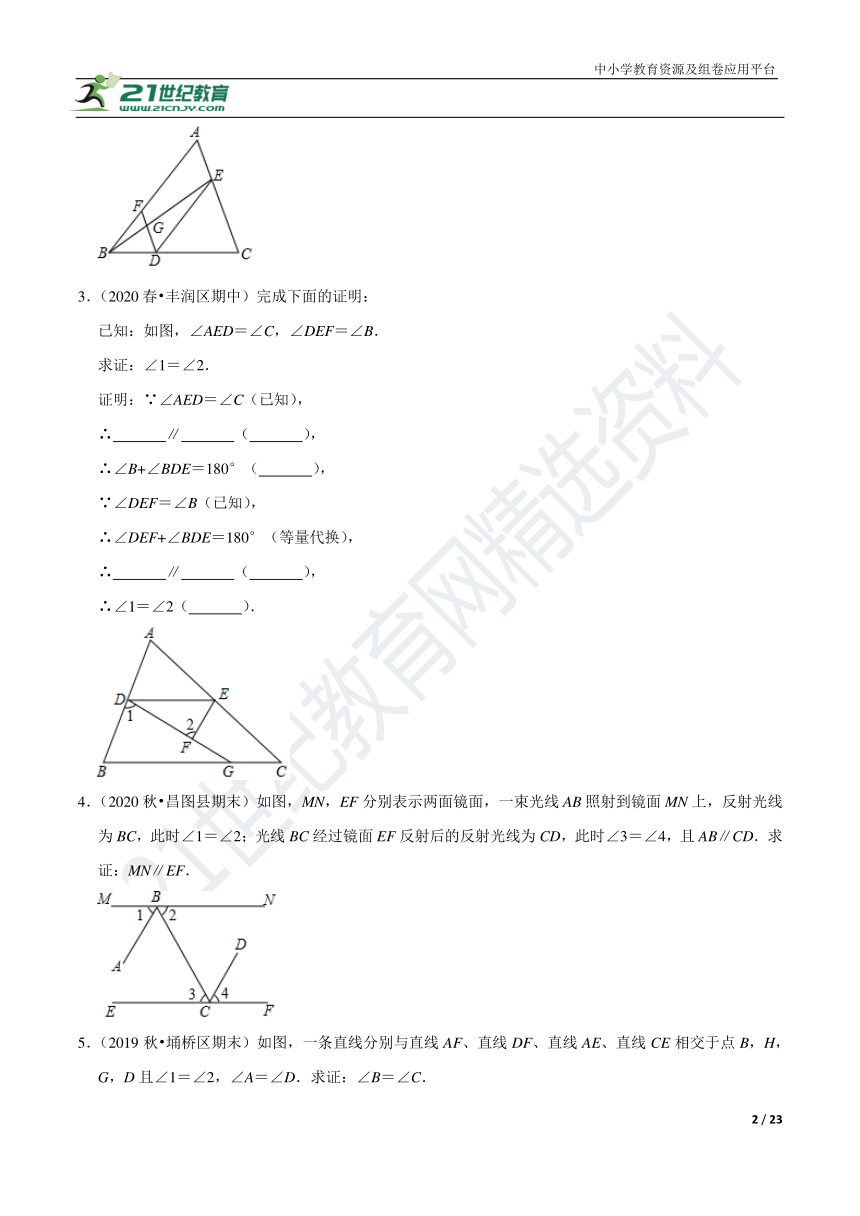
3.(2020春?丰润区期中)完成下面的证明:
已知:如图,∠AED=∠C,∠DEF=∠B.
求证:∠1=∠2.
证明:∵∠AED=∠C(已知),
∴ ∥ ( ),
∴∠B+∠BDE=180°( ),
∵∠DEF=∠B(已知),
∴∠DEF+∠BDE=180°(等量代换),
∴ ∥ ( ),
∴∠1=∠2( ).
4.(2020秋?昌图县期末)如图,MN,EF分别表示两面镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的反射光线为CD,此时∠3=∠4,且AB∥CD.求证:MN∥EF.
5.(2019秋?埇桥区期末)如图,一条直线分别与直线AF、直线DF、直线AE、直线CE相交于点B,H,G,D且∠1=∠2,∠A=∠D.求证:∠B=∠C.
6.(2019秋?上蔡县期末)如图,AD∥EF,∠1+∠2=180°,
(1)求证:DG∥AB;
(2)若DG是∠ADC的角平分线,∠1=30°,求∠B的度数.
7.(2019秋?泉州期末)如图,AD⊥BC于D点,EF⊥BC于F点,∠ADG=35°,∠C=55°.
(1)证明:DG∥AC;
(2)证明:∠FEC=∠ADG.
8.(2019秋?乐至县期末)已知:如图,∠1=∠2,∠3=∠B;
(1)求证:EF∥AB;
(2)求证:DE∥BC;
(3)若∠C=80°,求∠AED的度数.
9.(2020春?单县期末)已知:如图EF∥CD,∠1+∠2=180°.
(1)试说明GD∥CA;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数.
10.(2020春?溧阳市期末)如图,在△ABC中,点D在BC边上,EF∥AD,分别交AB、BC于点E、F,DG平分∠ADC,交AC于点G,∠1+∠2=180°.
(1)求证:DG∥AB;
(2)若∠B=32°,求∠ADC的度数.
11.(2019秋?万州区期末)如图,∠AEM+∠CDN=180°,EC平分∠AEF.若∠EFC=62°,求∠C的度数.根据提示将解题过程补充完整.
解:∵∠CDM+∠CDN=180°(平角),
又∵∠AEM+∠CDN=180°(已知),
∴∠AEM=∠CDM
∴AB∥CD,( )
∴∠AEF+( )=180°,(两直线平行,同旁内角互补)
∵∠EFC=62°,
∴∠AEF=( )
∵EC平分∠AEF,
∴∠AEC=( ).(角平分线的定义)
∵AB∥CD,
∴∠C=∠AEC=( )(两直线平行,内错角相等)
12.(2020春?润州区期末)结合图形填空:已知:如图,∠1=∠2,∠C=∠D.求证:∠A=∠F.
证明:∵∠1=∠2(已知),
又∠1=∠DMN( ),
∴∠2=∠DMN(等量代换),
∴DB∥EC(同位角相等,两直线平行),
∴∠DBC+∠C=180°( ).
又∵∠C=∠D(已知),
∴∠DBC+∠D=180°(等量代换),
∴DF∥AC( ),
∴∠A=∠F( ).
13.(2020秋?文山市期末)如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
14.(2019春?桥西区校级期中)已知,如图,在四边形ABCD中,AB∥CD,延长BC至点E,连接AE交CD于点F,使∠BAC=∠DAE,∠ACB=∠CFE
(1)求证:∠BAF=∠CAD;
(2)求证:AD∥BE;
(3)若BF平分∠ABC,请写出∠AFB与∠CAF的数量关系 .(不需证明)
15.(2020秋?南岗区期末)已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+12∠FGN,求∠MHG的度数.
16.(2020春?汉阳区校级期中)(1)如图1,AB∥CD,点M为直线AB,CD所确定的平面内的一点,若∠A=105°+α,∠M=108°﹣α,请直接写出∠C的度数 ;
(2)如图2,AB∥CD,点P为直线AB,CD所确定的平面内的一点,点E在直线CD上,AN平分∠PAB,射线AN的反向延长线交∠PCE的平分线于M,若∠P=30°,求∠AMC的度数;
(3)如图3,点P与直线AB,CD在同一平面内,AN平分∠PAB,射线AN的反向延长线交∠PCD的平分线于M,若∠AMC=180°-12∠P,求证:AB∥CD.
17.(2020春?黄陂区期末)如图,直线AB与CD交于点F,锐角∠CDE=α,∠AFC+α=180°.
(1)求证:AB∥DE;
(2)若G为直线AB(不与点F重合)上一点,∠FDG与∠DGB的角平分线所在的直线交于点P.
①如图2,α=50°,G为FB上一点,请补齐图形并求∠DPG的度数;
②直接写出∠DPG的度数为 (结果用含α的式子表示).
18.(2020秋?南岗区期中)已知,AE∥BD,∠A=∠D.
(1)如图1,求证:AB∥CD;
(2)如图2,作∠BAE的平分线交CD于点F,点G为AB上一点,连接FG,若∠CFG的平分线交线段AG于点H,求证:∠ECF+2∠AFH=∠E+2∠BHF;
(3)如图3,在(2)的条件下,连接AC,若∠ACE=∠BAC+∠BGM,过点H作HM⊥FH交FG的延长线于点M,且2∠E﹣3∠AFH=20°,求∠EAF+∠GMH的度数.
19.(2020春?汉阳区期末)如图,∠1+∠2=180°,∠B=∠3.
(1)判断DE与BC的位置关系,并说明理由;
(2)若∠C=63°,求∠DEC的度数.
20.(2020秋?南岗区期中)如图,AE平分∠BAC,∠CAE=∠CEA.
(1)如图1,求证:AB∥CD;
(2)如图2,点F为线段AC上一点,连接EF,求证:∠BAF+∠AFE+∠DEF=360°;
(3)如图3,在(2)的条件下,在射线AB上取点G,连接EG,使得∠GEF=∠C,当∠AEF=35°,∠GED=2∠GEF时,求∠C的度数.
答案
一.解答题(共20小题)
1.【解析】证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE(同旁内角互补,两直线平行).
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠P=∠Q(已知),
∴PB∥(CQ)(内错角相等,两直线平行).
∴∠PBC=(∠BCQ)(两直线平行,内错角相等).
∵∠1=∠ABC﹣(∠PBC),∠2=∠BCD﹣(∠BCQ),
∴∠1=∠2(等量代换).
故答案为:同旁内角互补,两直线平行;两直线平行,内错角相等;CQ,内错角相等,两直线平行;∠BCQ;∠PBC;∠BCQ.
2.【解析】证明:∵DE∥AB(已知),
∴∠A=∠CED(两直线平行,同位角相等)
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD(等量代换)
∴DF∥AE(同位角相等,两直线平行)
∴∠EGF+∠AEG=180°(两直线平行,同旁内角互补)
故答案为:两直线平行,同位角相等;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补.
3.【解析】∵∠AED=∠C(已知),
∴DE∥BC(同位角相等,两直线平行),
∴∠B+∠BDE=180° (两直线平行,同旁内角互补),
∵∠DEF=∠B(已知),
∴∠DEF+∠BDE=180° (等量代换),
∴EF∥AB(同旁内角互补,两直线平行),
∴∠1=∠2 (两直线平行,内错角相等).
故答案为:DE;BC;同位角相等,两直线平行;两直线平行,同旁内角互补;EF;AB;同旁内角互补,两直线平行;两直线平行,内错角相等.
4.【解析】证明:∵AB∥CD,
∴∠ABC=∠BCD,
∵∠1+∠ABC+∠2=∠3+∠BCD+∠4=180°,
∴∠1+∠2=∠3+∠4,
又∵∠1=∠2,∠3=∠4,
∴∠2=∠3,
∴MN∥EF.
5.【解析】证明:∵∠1=∠2,
∴AE∥DF,
∴∠AEC=∠D.
又∵∠A=∠D,
∴∠AEC=∠A,
∴AB∥CD,
∴∠B=∠C.
6.【解析】(1)证明:∵AD∥EF(已知),
∴∠2+∠BAD=180°(两直线平行,同旁内角互补),
又∵∠1+∠2=180°(已知),
∴∠1=∠BAD(同角的补角相等),
∴DG∥AB (内错角相等,两直线平行);
(2)∵DG是∠ADC的角平分线,
∴∠GDC=∠1=30°,
又∵DG∥AB,
∴∠B=∠GDC=30°.
7.【解析】证明:(1)∵AD⊥BC于D点,∠ADG=35°,
∴∠BDG=90°﹣35°=55°,
又∵∠C=55°,
∴∠BDG=∠C,
∴DG∥AC;
(2)∵AD⊥BC于D点,EF⊥BC于F点,
∴AD∥EF,
∴∠CEF=∠CAD,
又∵DG∥AC,
∴∠ADG=∠CAD,
∴∠FEC=∠ADG.
8.【解析】(1)证明:∵∠1=∠2,
∴EF∥AB;
(2)∵EF∥AB,
∴∠3=∠ADE,
∵∠3=∠B,
∴∠ADE=∠B,
∴DE∥BC;
(3)∵DE∥BC,
∴∠AED=∠C,
∵∠C=80°,
∴∠AED=80°.
9.【解析】(1)∵EF∥CD
∴∠1+∠ECD=180°
又∵∠1+∠2=180°
∴∠2=∠ECD
∴GD∥CA
(2)由(1)得:GD∥CA,
∴∠BDG=∠A=40°,∠ACD=∠2,
∵DG平分∠CDB,
∴∠2=∠BDG=40°,
∴∠ACD=∠2=40°,
∵CD平分∠ACB,
∴∠ACB=2∠ACD=80°.
10.【解析】(1)证明:∵EF∥AD,
∴∠2+∠3=180°.
∵∠1+∠2=180°.
∴∠1=∠3.
∴DG∥AB;
(2)∵DG平分∠ADC,
∴∠ADC=2∠1=2∠4.
由(1)知DG∥AB,
∴∠4=∠B=32°,
∴∠ADC=2∠4=64°.
11.【解析】∵∠CDM+∠CDN=180°(平角),
又∵∠AEM+∠CDN=180°(已知),
∴∠AEM=∠CDM(同角的补角相等),
∴AB∥CD,(同位角相等,两直线平行)
∴∠AEF+(∠EFC)=180°,(两直线平行,同旁内角互补)
∵∠EFC=62°,
∴∠AEF=(118°)
∵EC平分∠AEF,
∴∠AEC=(59°).(角平分线的定义)
∵AB∥CD,
∴∠C=∠AEC=(59°)(两直线平行,内错角相等).
故答案为:同位角相等,两直线平行;∠EFC;118°;59°;59°.
12.【解析】证明:∵∠1=∠2(已知),
又∠1=∠DMN(对顶角相等),
∴∠2=∠DMN(等量代换),
∴DB∥EC(同位角相等,两直线平行),
∴∠DBC+∠C=180°(两直线平行,同旁内角互补).
又∵∠C=∠D(已知),
∴∠DBC+∠D=180°(等量代换),
∴DF∥AC(同旁内角互补,两直线平行),
∴∠A=∠F(两直线平行,内错角相等).
故答案为:对顶角相等;两直线平行,同旁内角互补;同旁内角互补,两直线平行;两直线平行,内错角相等.
13.【解析】∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
14.【解析】(1)∵∠BAC=∠DAE,
∴∠BAC+∠CAF=∠DAE+∠CAF,
∴∠BAF=∠CAD;
(2)∵∠BAC=∠DAF,∠ACB=∠CFE=∠AFD,
∴∠B=∠D,
∵AB∥CD,
∴∠B+∠BCD=180°,
∴∠D+∠BCD=180°,
∴AD∥BE;
(3)如图2,∵AD∥BE,
∴∠E=∠1=∠2,
∵BF平分∠ABC,
∴∠3=∠4,
∵∠AFB是△BEF的外角,
∴∠AFB=∠4+∠E=∠4+∠1,
∴∠AFB=3+∠2,
又∵AD∥BC,
∴∠ABC+∠BAD=180°,
∴∠3+∠4+∠1+∠CAF+∠2=180°,
即2∠AFB+∠CAF=180°.
故答案为:2∠AFB+∠CAF=180°.
15.【解析】(1)证明:如图1,∵∠AGE+∠DHE=180°,∠AGE=∠BGF.
∴∠BGF+∠DHE=180°,
∴AB∥CD;
(2)证明:如图2,过点M作MR∥AB,
又∵AB∥CD,
∴AB∥CD∥MR.
∴∠GMR=∠AGM,∠HMR=∠CHM.
∴∠EGF=∠AEG+∠GFC;
(3)解:如图3,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β,
∵射线GH是∠BGM的平分线,
∴∠FGM=12∠BGM=12(180°-∠AGM)=90°-α,
∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,
∵∠M=∠N+12∠FGN,
∴2α+β=2α+12∠FGN,
∴∠FGN=2β,
过点N作HT∥GN,
则∠MHT=∠N=2α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+2β,
∠CGH=∠CHM+∠MHT+∠GHT=β+2α+2β=2α+3β,
∵AB∥CD,
∴∠AGH+∠CGH=180°,
∴90°+α+2α+3β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
16.【解析】(1)如图1,连接AC,
在△AMC中,∠AMC+∠MAC+∠MCA=180°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠BAM+∠M+∠MCD=180°+180°=360°,
∵∠BAM=105°+α,∠M=108°﹣α,
∴∠MCD=360°﹣[105°+α+(108°﹣α)]=147°,
故答案为:147°;
(2)如图2,延长BA与CP交于点Q,CQ与AM交于点H,
∵AN平分∠PAB,
∴∠BAN=∠PAN,
∴∠QAP=180°﹣2∠BAN,
∵∠P=30°,
∴∠CQA=∠P+∠QAP=30°+180°﹣2∠BAN=210﹣2∠BAN,
∠MHC=∠NHP=∠NAP﹣∠P=∠BAN﹣30°,
∵AB∥CD,
∴∠ECQ=∠CQA=210°﹣2∠BAN,
∵CM平分∠PCE,
∴∠MCH=12∠ECP=12×(210°﹣2∠BAN)=105°﹣∠BAN,
∵∠AMC=180°﹣∠MHC﹣∠MCH,
∴∠AMC=180°﹣(∠BAN﹣30°)﹣(105°﹣∠BAN)=105°;
(3)如图3,连接AC,
则∠PAC+∠PCA=180°﹣∠P,∠MAC+∠MCA=180°﹣∠M,
∵∠AMC=180°-12∠D,
∴∠MAC+∠MCA=12∠P,
∴∠MAC+∠MCA+∠PAC+∠PA=180°-12∠P,
即∠PAM+∠PCM=180°-12∠P,
∵AN平分∠PAB,MC平分∠PCD,
∴∠BAM=∠PAM,∠DCM=∠PCM,
∴∠BAM+∠DCM=180°-12∠P,
∴∠BCA+∠DCA=180°-12∠P+12∠P=180°,
∴AB∥CD.
17.【解析】(1)证明:∵∠AFC+∠AFD=180°,∠AFC+α=180°,
∴∠AFD=α=∠CDE,
∴AB∥DE;
(2)解:①如图即为补齐的图形,
∵∠FDG与∠DGB的角平分线所在的直线交于点P,
∴∠FDG=2∠FDP=2∠GDP,∠DGB=2∠DGQ=2∠BGQ,
由(1)知AB∥DE,
∴∠DFB=180°﹣α=180°﹣50°=130°,
∵∠DGB=∠FDG+∠DFG,
∴2∠DGQ=2∠GDP+130°,
∴∠DGQ=∠GDP+65°,
∵∠DGQ=∠GDP+∠DPG,
∴∠DPG=65°;
②由①知∠DPG=12∠DFB=12(180°﹣α)=90°-12α.
故答案为:90°-12α.
18.【解析】(1)证明:∵AE∥BD,
∴∠A+∠B=180°,
∵∠A=∠D,
∴∠D+∠B=180°,
∴AB∥CD;
(2)证明:如图2,过点E作EP∥CD,
∵AB∥CD,
∴AB∥EP,
∴∠PEA=∠EAB,∠PEC=∠ECF,
∵∠AEC=∠PEC﹣∠PEA,
∴∠AEC=∠ECF﹣∠EAB,
即∠ECF=∠AEC+∠EAB,
∵AF是∠BAE的平分线,
∴∠EAF=∠FAB=12∠EAB,
∵FH是∠CFG的平分线,
∴∠CFH=∠HFG=12∠CFG,
∵CD∥AB,
∴∠BHF=∠CFH,∠CFA=∠FAB,
设∠FAB=α,∠CFH=β,
∵∠AFH=∠CFH﹣∠CFA=∠CFH﹣∠FAB,
∴∠AFH=β﹣α,∠BHF=∠CFH=β,
∴∠ECF+2∠AFH=∠AEC+∠EAB+2∠AFH=∠AEC+2α+2(β﹣α)=∠AEC+2β,
∴∠ECF+2∠AFH=∠E+2∠BHF;
(3)解:如图,延长DC至点Q,
∵AB∥CD,
∴∠QCA=∠CAB,∠BGM=∠DFG,∠CFH=∠BHF,∠CFA=∠FAG,
∵∠ACE=∠BAC+∠BGM,
∴∠ECQ+∠QCA=∠BAC+∠BGM,
∴∠ECQ=∠BGM=∠DFG,
∵∠ECQ+∠ECD=180°,∠DFG+∠CFG=180°,
∴∠ECF=∠CFG,
由(2)问知:∠ECF+2∠AFH=∠AEC+2∠BHF,∠CFG=2∠CFH=2∠BHF,
∴∠AEC=2∠AFH,
∵2∠AEC﹣3∠AFH=20°,
∴∠AFH=20°,
由(2)问知:∠CFM=2β,∠FHG=β,
∵FH⊥HM,
∴∠FHM=90°,
∴∠GHM=90°﹣β,
过点M作MN∥AB,
∴MN∥CD,
∴∠CFM+∠NMF=180°,∠GHM=∠HMN=90°﹣β,
∴∠HMB=∠HMN=90°﹣β,
由(2)问知:∠EAF=∠FAB,
∴∠EAF=∠CFA=∠CFH﹣∠AFH=β﹣20°,
∴∠EAF+∠GMH=β﹣20°+90°﹣β=70°,
∴∠EAF+∠GMH=70°.
19.【解析】(1)DE∥BC.
理由:∵∠1+∠2=180°,
∴AB∥EF,
∴∠ADE=∠3,
∵∠B=∠3,
∴∠ADE=∠B,
∴DE∥BC;
(2)∵DE∥BC,
∴∠C+∠DEC=180°,
∵∠C=63°,
∴∠DEC=117°.
20.【解析】(1)证明:∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠CAE=∠CEA,
∴∠CEA=∠BAE,
∴AB∥CD;
(2)证明:过F作FM∥AB,如图,
∵AB∥CD,
∴AB∥FM∥CD,
∴∠BAF+∠AFE=180°,∠DEF+∠EFM=180°,
∴∠BAF+∠AFM+∠DEF+∠EFM=360°,
即∠BAF+∠AFE+∠DEF=360°;
(3)解:设∠GEF=∠C=x°,
∵∠GEF=∠C,∠GED=2∠GEF,
∴∠GED=2x°,
∵AB∥CD,
∴∠C+∠BAC=180°,
∴∠BAC=180°﹣x°,
∵AE平分∠BAC,
∴∠BAE=12∠BAC=12(180°﹣x°)=90°-12x°,
由(1)知:AB∥CD,
∴∠BAE+∠AED=180°,
∵∠AEF=35°,
∴90-12x+x﹣35+2x=180,
解得:x=50,
即∠C=50°.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一.解答题(共20小题)
1.(2020秋?长春期末)如图,∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
在下列解答中,填空:
证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE( ).
∴∠ABC=∠BCD( ).
∵∠P=∠Q(已知),
∴PB∥( )( ).
∴∠PBC=( )(两直线平行,内错角相等).
∵∠1=∠ABC﹣( ),∠2=∠BCD﹣( ),
∴∠1=∠2(等量代换).
2.(2020秋?松北区期末)完成下面的证明:
如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
证明:∵DE∥AB(已知),
∴∠A=∠CED( )
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD( )
∴DF∥AE( )
∴∠EGF+∠AEG=180°( )
3.(2020春?丰润区期中)完成下面的证明:
已知:如图,∠AED=∠C,∠DEF=∠B.
求证:∠1=∠2.
证明:∵∠AED=∠C(已知),
∴ ∥ ( ),
∴∠B+∠BDE=180°( ),
∵∠DEF=∠B(已知),
∴∠DEF+∠BDE=180°(等量代换),
∴ ∥ ( ),
∴∠1=∠2( ).
4.(2020秋?昌图县期末)如图,MN,EF分别表示两面镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的反射光线为CD,此时∠3=∠4,且AB∥CD.求证:MN∥EF.
5.(2019秋?埇桥区期末)如图,一条直线分别与直线AF、直线DF、直线AE、直线CE相交于点B,H,G,D且∠1=∠2,∠A=∠D.求证:∠B=∠C.
6.(2019秋?上蔡县期末)如图,AD∥EF,∠1+∠2=180°,
(1)求证:DG∥AB;
(2)若DG是∠ADC的角平分线,∠1=30°,求∠B的度数.
7.(2019秋?泉州期末)如图,AD⊥BC于D点,EF⊥BC于F点,∠ADG=35°,∠C=55°.
(1)证明:DG∥AC;
(2)证明:∠FEC=∠ADG.
8.(2019秋?乐至县期末)已知:如图,∠1=∠2,∠3=∠B;
(1)求证:EF∥AB;
(2)求证:DE∥BC;
(3)若∠C=80°,求∠AED的度数.
9.(2020春?单县期末)已知:如图EF∥CD,∠1+∠2=180°.
(1)试说明GD∥CA;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数.
10.(2020春?溧阳市期末)如图,在△ABC中,点D在BC边上,EF∥AD,分别交AB、BC于点E、F,DG平分∠ADC,交AC于点G,∠1+∠2=180°.
(1)求证:DG∥AB;
(2)若∠B=32°,求∠ADC的度数.
11.(2019秋?万州区期末)如图,∠AEM+∠CDN=180°,EC平分∠AEF.若∠EFC=62°,求∠C的度数.根据提示将解题过程补充完整.
解:∵∠CDM+∠CDN=180°(平角),
又∵∠AEM+∠CDN=180°(已知),
∴∠AEM=∠CDM
∴AB∥CD,( )
∴∠AEF+( )=180°,(两直线平行,同旁内角互补)
∵∠EFC=62°,
∴∠AEF=( )
∵EC平分∠AEF,
∴∠AEC=( ).(角平分线的定义)
∵AB∥CD,
∴∠C=∠AEC=( )(两直线平行,内错角相等)
12.(2020春?润州区期末)结合图形填空:已知:如图,∠1=∠2,∠C=∠D.求证:∠A=∠F.
证明:∵∠1=∠2(已知),
又∠1=∠DMN( ),
∴∠2=∠DMN(等量代换),
∴DB∥EC(同位角相等,两直线平行),
∴∠DBC+∠C=180°( ).
又∵∠C=∠D(已知),
∴∠DBC+∠D=180°(等量代换),
∴DF∥AC( ),
∴∠A=∠F( ).
13.(2020秋?文山市期末)如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
14.(2019春?桥西区校级期中)已知,如图,在四边形ABCD中,AB∥CD,延长BC至点E,连接AE交CD于点F,使∠BAC=∠DAE,∠ACB=∠CFE
(1)求证:∠BAF=∠CAD;
(2)求证:AD∥BE;
(3)若BF平分∠ABC,请写出∠AFB与∠CAF的数量关系 .(不需证明)
15.(2020秋?南岗区期末)已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+12∠FGN,求∠MHG的度数.
16.(2020春?汉阳区校级期中)(1)如图1,AB∥CD,点M为直线AB,CD所确定的平面内的一点,若∠A=105°+α,∠M=108°﹣α,请直接写出∠C的度数 ;
(2)如图2,AB∥CD,点P为直线AB,CD所确定的平面内的一点,点E在直线CD上,AN平分∠PAB,射线AN的反向延长线交∠PCE的平分线于M,若∠P=30°,求∠AMC的度数;
(3)如图3,点P与直线AB,CD在同一平面内,AN平分∠PAB,射线AN的反向延长线交∠PCD的平分线于M,若∠AMC=180°-12∠P,求证:AB∥CD.
17.(2020春?黄陂区期末)如图,直线AB与CD交于点F,锐角∠CDE=α,∠AFC+α=180°.
(1)求证:AB∥DE;
(2)若G为直线AB(不与点F重合)上一点,∠FDG与∠DGB的角平分线所在的直线交于点P.
①如图2,α=50°,G为FB上一点,请补齐图形并求∠DPG的度数;
②直接写出∠DPG的度数为 (结果用含α的式子表示).
18.(2020秋?南岗区期中)已知,AE∥BD,∠A=∠D.
(1)如图1,求证:AB∥CD;
(2)如图2,作∠BAE的平分线交CD于点F,点G为AB上一点,连接FG,若∠CFG的平分线交线段AG于点H,求证:∠ECF+2∠AFH=∠E+2∠BHF;
(3)如图3,在(2)的条件下,连接AC,若∠ACE=∠BAC+∠BGM,过点H作HM⊥FH交FG的延长线于点M,且2∠E﹣3∠AFH=20°,求∠EAF+∠GMH的度数.
19.(2020春?汉阳区期末)如图,∠1+∠2=180°,∠B=∠3.
(1)判断DE与BC的位置关系,并说明理由;
(2)若∠C=63°,求∠DEC的度数.
20.(2020秋?南岗区期中)如图,AE平分∠BAC,∠CAE=∠CEA.
(1)如图1,求证:AB∥CD;
(2)如图2,点F为线段AC上一点,连接EF,求证:∠BAF+∠AFE+∠DEF=360°;
(3)如图3,在(2)的条件下,在射线AB上取点G,连接EG,使得∠GEF=∠C,当∠AEF=35°,∠GED=2∠GEF时,求∠C的度数.
答案
一.解答题(共20小题)
1.【解析】证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE(同旁内角互补,两直线平行).
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠P=∠Q(已知),
∴PB∥(CQ)(内错角相等,两直线平行).
∴∠PBC=(∠BCQ)(两直线平行,内错角相等).
∵∠1=∠ABC﹣(∠PBC),∠2=∠BCD﹣(∠BCQ),
∴∠1=∠2(等量代换).
故答案为:同旁内角互补,两直线平行;两直线平行,内错角相等;CQ,内错角相等,两直线平行;∠BCQ;∠PBC;∠BCQ.
2.【解析】证明:∵DE∥AB(已知),
∴∠A=∠CED(两直线平行,同位角相等)
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD(等量代换)
∴DF∥AE(同位角相等,两直线平行)
∴∠EGF+∠AEG=180°(两直线平行,同旁内角互补)
故答案为:两直线平行,同位角相等;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补.
3.【解析】∵∠AED=∠C(已知),
∴DE∥BC(同位角相等,两直线平行),
∴∠B+∠BDE=180° (两直线平行,同旁内角互补),
∵∠DEF=∠B(已知),
∴∠DEF+∠BDE=180° (等量代换),
∴EF∥AB(同旁内角互补,两直线平行),
∴∠1=∠2 (两直线平行,内错角相等).
故答案为:DE;BC;同位角相等,两直线平行;两直线平行,同旁内角互补;EF;AB;同旁内角互补,两直线平行;两直线平行,内错角相等.
4.【解析】证明:∵AB∥CD,
∴∠ABC=∠BCD,
∵∠1+∠ABC+∠2=∠3+∠BCD+∠4=180°,
∴∠1+∠2=∠3+∠4,
又∵∠1=∠2,∠3=∠4,
∴∠2=∠3,
∴MN∥EF.
5.【解析】证明:∵∠1=∠2,
∴AE∥DF,
∴∠AEC=∠D.
又∵∠A=∠D,
∴∠AEC=∠A,
∴AB∥CD,
∴∠B=∠C.
6.【解析】(1)证明:∵AD∥EF(已知),
∴∠2+∠BAD=180°(两直线平行,同旁内角互补),
又∵∠1+∠2=180°(已知),
∴∠1=∠BAD(同角的补角相等),
∴DG∥AB (内错角相等,两直线平行);
(2)∵DG是∠ADC的角平分线,
∴∠GDC=∠1=30°,
又∵DG∥AB,
∴∠B=∠GDC=30°.
7.【解析】证明:(1)∵AD⊥BC于D点,∠ADG=35°,
∴∠BDG=90°﹣35°=55°,
又∵∠C=55°,
∴∠BDG=∠C,
∴DG∥AC;
(2)∵AD⊥BC于D点,EF⊥BC于F点,
∴AD∥EF,
∴∠CEF=∠CAD,
又∵DG∥AC,
∴∠ADG=∠CAD,
∴∠FEC=∠ADG.
8.【解析】(1)证明:∵∠1=∠2,
∴EF∥AB;
(2)∵EF∥AB,
∴∠3=∠ADE,
∵∠3=∠B,
∴∠ADE=∠B,
∴DE∥BC;
(3)∵DE∥BC,
∴∠AED=∠C,
∵∠C=80°,
∴∠AED=80°.
9.【解析】(1)∵EF∥CD
∴∠1+∠ECD=180°
又∵∠1+∠2=180°
∴∠2=∠ECD
∴GD∥CA
(2)由(1)得:GD∥CA,
∴∠BDG=∠A=40°,∠ACD=∠2,
∵DG平分∠CDB,
∴∠2=∠BDG=40°,
∴∠ACD=∠2=40°,
∵CD平分∠ACB,
∴∠ACB=2∠ACD=80°.
10.【解析】(1)证明:∵EF∥AD,
∴∠2+∠3=180°.
∵∠1+∠2=180°.
∴∠1=∠3.
∴DG∥AB;
(2)∵DG平分∠ADC,
∴∠ADC=2∠1=2∠4.
由(1)知DG∥AB,
∴∠4=∠B=32°,
∴∠ADC=2∠4=64°.
11.【解析】∵∠CDM+∠CDN=180°(平角),
又∵∠AEM+∠CDN=180°(已知),
∴∠AEM=∠CDM(同角的补角相等),
∴AB∥CD,(同位角相等,两直线平行)
∴∠AEF+(∠EFC)=180°,(两直线平行,同旁内角互补)
∵∠EFC=62°,
∴∠AEF=(118°)
∵EC平分∠AEF,
∴∠AEC=(59°).(角平分线的定义)
∵AB∥CD,
∴∠C=∠AEC=(59°)(两直线平行,内错角相等).
故答案为:同位角相等,两直线平行;∠EFC;118°;59°;59°.
12.【解析】证明:∵∠1=∠2(已知),
又∠1=∠DMN(对顶角相等),
∴∠2=∠DMN(等量代换),
∴DB∥EC(同位角相等,两直线平行),
∴∠DBC+∠C=180°(两直线平行,同旁内角互补).
又∵∠C=∠D(已知),
∴∠DBC+∠D=180°(等量代换),
∴DF∥AC(同旁内角互补,两直线平行),
∴∠A=∠F(两直线平行,内错角相等).
故答案为:对顶角相等;两直线平行,同旁内角互补;同旁内角互补,两直线平行;两直线平行,内错角相等.
13.【解析】∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
14.【解析】(1)∵∠BAC=∠DAE,
∴∠BAC+∠CAF=∠DAE+∠CAF,
∴∠BAF=∠CAD;
(2)∵∠BAC=∠DAF,∠ACB=∠CFE=∠AFD,
∴∠B=∠D,
∵AB∥CD,
∴∠B+∠BCD=180°,
∴∠D+∠BCD=180°,
∴AD∥BE;
(3)如图2,∵AD∥BE,
∴∠E=∠1=∠2,
∵BF平分∠ABC,
∴∠3=∠4,
∵∠AFB是△BEF的外角,
∴∠AFB=∠4+∠E=∠4+∠1,
∴∠AFB=3+∠2,
又∵AD∥BC,
∴∠ABC+∠BAD=180°,
∴∠3+∠4+∠1+∠CAF+∠2=180°,
即2∠AFB+∠CAF=180°.
故答案为:2∠AFB+∠CAF=180°.
15.【解析】(1)证明:如图1,∵∠AGE+∠DHE=180°,∠AGE=∠BGF.
∴∠BGF+∠DHE=180°,
∴AB∥CD;
(2)证明:如图2,过点M作MR∥AB,
又∵AB∥CD,
∴AB∥CD∥MR.
∴∠GMR=∠AGM,∠HMR=∠CHM.
∴∠EGF=∠AEG+∠GFC;
(3)解:如图3,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β,
∵射线GH是∠BGM的平分线,
∴∠FGM=12∠BGM=12(180°-∠AGM)=90°-α,
∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,
∵∠M=∠N+12∠FGN,
∴2α+β=2α+12∠FGN,
∴∠FGN=2β,
过点N作HT∥GN,
则∠MHT=∠N=2α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+2β,
∠CGH=∠CHM+∠MHT+∠GHT=β+2α+2β=2α+3β,
∵AB∥CD,
∴∠AGH+∠CGH=180°,
∴90°+α+2α+3β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
16.【解析】(1)如图1,连接AC,
在△AMC中,∠AMC+∠MAC+∠MCA=180°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠BAM+∠M+∠MCD=180°+180°=360°,
∵∠BAM=105°+α,∠M=108°﹣α,
∴∠MCD=360°﹣[105°+α+(108°﹣α)]=147°,
故答案为:147°;
(2)如图2,延长BA与CP交于点Q,CQ与AM交于点H,
∵AN平分∠PAB,
∴∠BAN=∠PAN,
∴∠QAP=180°﹣2∠BAN,
∵∠P=30°,
∴∠CQA=∠P+∠QAP=30°+180°﹣2∠BAN=210﹣2∠BAN,
∠MHC=∠NHP=∠NAP﹣∠P=∠BAN﹣30°,
∵AB∥CD,
∴∠ECQ=∠CQA=210°﹣2∠BAN,
∵CM平分∠PCE,
∴∠MCH=12∠ECP=12×(210°﹣2∠BAN)=105°﹣∠BAN,
∵∠AMC=180°﹣∠MHC﹣∠MCH,
∴∠AMC=180°﹣(∠BAN﹣30°)﹣(105°﹣∠BAN)=105°;
(3)如图3,连接AC,
则∠PAC+∠PCA=180°﹣∠P,∠MAC+∠MCA=180°﹣∠M,
∵∠AMC=180°-12∠D,
∴∠MAC+∠MCA=12∠P,
∴∠MAC+∠MCA+∠PAC+∠PA=180°-12∠P,
即∠PAM+∠PCM=180°-12∠P,
∵AN平分∠PAB,MC平分∠PCD,
∴∠BAM=∠PAM,∠DCM=∠PCM,
∴∠BAM+∠DCM=180°-12∠P,
∴∠BCA+∠DCA=180°-12∠P+12∠P=180°,
∴AB∥CD.
17.【解析】(1)证明:∵∠AFC+∠AFD=180°,∠AFC+α=180°,
∴∠AFD=α=∠CDE,
∴AB∥DE;
(2)解:①如图即为补齐的图形,
∵∠FDG与∠DGB的角平分线所在的直线交于点P,
∴∠FDG=2∠FDP=2∠GDP,∠DGB=2∠DGQ=2∠BGQ,
由(1)知AB∥DE,
∴∠DFB=180°﹣α=180°﹣50°=130°,
∵∠DGB=∠FDG+∠DFG,
∴2∠DGQ=2∠GDP+130°,
∴∠DGQ=∠GDP+65°,
∵∠DGQ=∠GDP+∠DPG,
∴∠DPG=65°;
②由①知∠DPG=12∠DFB=12(180°﹣α)=90°-12α.
故答案为:90°-12α.
18.【解析】(1)证明:∵AE∥BD,
∴∠A+∠B=180°,
∵∠A=∠D,
∴∠D+∠B=180°,
∴AB∥CD;
(2)证明:如图2,过点E作EP∥CD,
∵AB∥CD,
∴AB∥EP,
∴∠PEA=∠EAB,∠PEC=∠ECF,
∵∠AEC=∠PEC﹣∠PEA,
∴∠AEC=∠ECF﹣∠EAB,
即∠ECF=∠AEC+∠EAB,
∵AF是∠BAE的平分线,
∴∠EAF=∠FAB=12∠EAB,
∵FH是∠CFG的平分线,
∴∠CFH=∠HFG=12∠CFG,
∵CD∥AB,
∴∠BHF=∠CFH,∠CFA=∠FAB,
设∠FAB=α,∠CFH=β,
∵∠AFH=∠CFH﹣∠CFA=∠CFH﹣∠FAB,
∴∠AFH=β﹣α,∠BHF=∠CFH=β,
∴∠ECF+2∠AFH=∠AEC+∠EAB+2∠AFH=∠AEC+2α+2(β﹣α)=∠AEC+2β,
∴∠ECF+2∠AFH=∠E+2∠BHF;
(3)解:如图,延长DC至点Q,
∵AB∥CD,
∴∠QCA=∠CAB,∠BGM=∠DFG,∠CFH=∠BHF,∠CFA=∠FAG,
∵∠ACE=∠BAC+∠BGM,
∴∠ECQ+∠QCA=∠BAC+∠BGM,
∴∠ECQ=∠BGM=∠DFG,
∵∠ECQ+∠ECD=180°,∠DFG+∠CFG=180°,
∴∠ECF=∠CFG,
由(2)问知:∠ECF+2∠AFH=∠AEC+2∠BHF,∠CFG=2∠CFH=2∠BHF,
∴∠AEC=2∠AFH,
∵2∠AEC﹣3∠AFH=20°,
∴∠AFH=20°,
由(2)问知:∠CFM=2β,∠FHG=β,
∵FH⊥HM,
∴∠FHM=90°,
∴∠GHM=90°﹣β,
过点M作MN∥AB,
∴MN∥CD,
∴∠CFM+∠NMF=180°,∠GHM=∠HMN=90°﹣β,
∴∠HMB=∠HMN=90°﹣β,
由(2)问知:∠EAF=∠FAB,
∴∠EAF=∠CFA=∠CFH﹣∠AFH=β﹣20°,
∴∠EAF+∠GMH=β﹣20°+90°﹣β=70°,
∴∠EAF+∠GMH=70°.
19.【解析】(1)DE∥BC.
理由:∵∠1+∠2=180°,
∴AB∥EF,
∴∠ADE=∠3,
∵∠B=∠3,
∴∠ADE=∠B,
∴DE∥BC;
(2)∵DE∥BC,
∴∠C+∠DEC=180°,
∵∠C=63°,
∴∠DEC=117°.
20.【解析】(1)证明:∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠CAE=∠CEA,
∴∠CEA=∠BAE,
∴AB∥CD;
(2)证明:过F作FM∥AB,如图,
∵AB∥CD,
∴AB∥FM∥CD,
∴∠BAF+∠AFE=180°,∠DEF+∠EFM=180°,
∴∠BAF+∠AFM+∠DEF+∠EFM=360°,
即∠BAF+∠AFE+∠DEF=360°;
(3)解:设∠GEF=∠C=x°,
∵∠GEF=∠C,∠GED=2∠GEF,
∴∠GED=2x°,
∵AB∥CD,
∴∠C+∠BAC=180°,
∴∠BAC=180°﹣x°,
∵AE平分∠BAC,
∴∠BAE=12∠BAC=12(180°﹣x°)=90°-12x°,
由(1)知:AB∥CD,
∴∠BAE+∠AED=180°,
∵∠AEF=35°,
∴90-12x+x﹣35+2x=180,
解得:x=50,
即∠C=50°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
