第2章 相交线与平行线单元测试卷(培优)(含解析)
文档属性
| 名称 | 第2章 相交线与平行线单元测试卷(培优)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 00:00:00 | ||
图片预览



文档简介
第2章相交线与平行线单元测试(培优)
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分120分,试题共26题,选择10道、填空8道、解答8道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020秋?玉田县期末)如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC的度数为( )
A.43° B.34° C.56° D.50°
2.(2020秋?鄂州期末)如图所示,点O在直线AB上,OE平分∠AOC,∠EOF=90°,则∠COF与∠AOE的关系是( )
A.相等 B.互余 C.互补 D.无法确定
3.(2020秋?新宾县期末)已知∠1和∠2互为余角,且∠2与∠3互补,∠1=60°,则∠3为( )
A.120° B.60° C.30° D.150°
4.(2020秋?长春期末)如图,∠B的内错角是( )
A.∠1 B.∠2 C.∠3 D.∠4
5.(2020春?威县期末)如图,把河AB中的水引到C,拟修水渠中最短的是( )
A.CM B.CN C.CP D.CQ
6.(2020秋?铁西区期末)如图,直线AB,CD相交于点O,射线OM平分∠BOD,若∠BOD=42°,则∠AOM等于( )
A.138° B.148° C.159° D.169°
7.(2020秋?龙岗区期末)下列命题中,是假命题的是( )
A.对顶角相等
B.两点之间,线段最短
C.互补的两个角不一定相等
D.同位角相等
8.(2020春?兴国县期末)如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l1∥l2的有( )
A.5个 B.4个 C.3个 D.2个
9.(2019秋?昌平区校级期末)一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时,BC∥DE,则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为( )
A.60°和135° B.45°、60°、105°和135°
C.30°和45° D.以上都有可能
10.(2020秋?邢台期中)观察如图,并阅读图形下面的相关文字:
两条直线相交,最多有1个交点;三条直线相交,最多有3个交点;4条直线相交,最多有6个交点……
像这样,20条直线相交,交点最多的个数是( )
A.100个 B.135个 C.190个 D.200个
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020秋?肇源县期末)两条直线相交所构成的四个角,其中:①有三个角都相等;②有一对对顶角相等;③有一个角是直角;④有一对邻补角相等,能判定这两条直线垂直的有 .
12.(2020秋?香坊区期末)两个角的两边两两互相平行,且一个角的12等于另一个角的13,则这两个角中较小角的度数为 °.
13.(2020秋?德惠市期末)如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1= .
14.(2020?安徽一模)如图,a∥b,∠2=95°,∠3=150°,则∠1的度数是 .
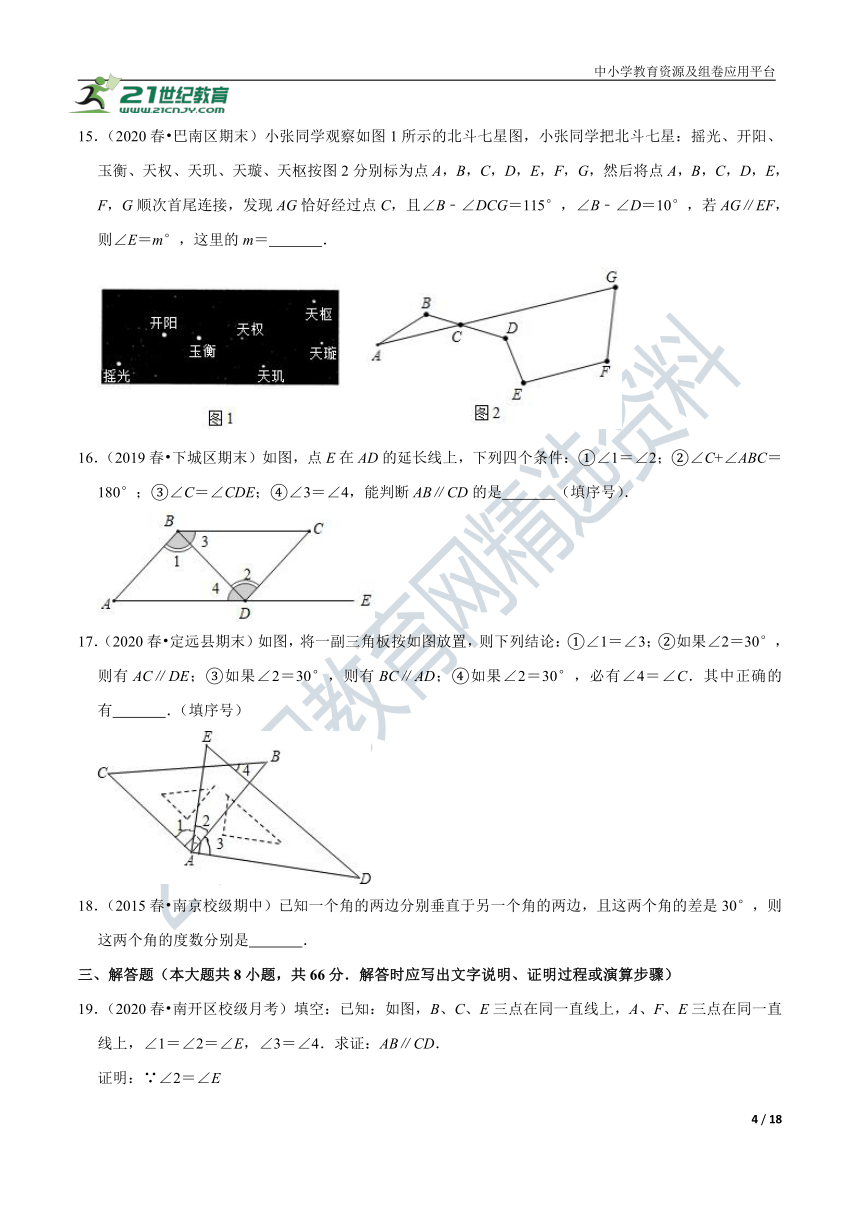
15.(2020春?巴南区期末)小张同学观察如图1所示的北斗七星图,小张同学把北斗七星:摇光、开阳、玉衡、天权、天玑、天璇、天枢按图2分别标为点A,B,C,D,E,F,G,然后将点A,B,C,D,E,F,G顺次首尾连接,发现AG恰好经过点C,且∠B﹣∠DCG=115°,∠B﹣∠D=10°,若AG∥EF,则∠E=m°,这里的m= .
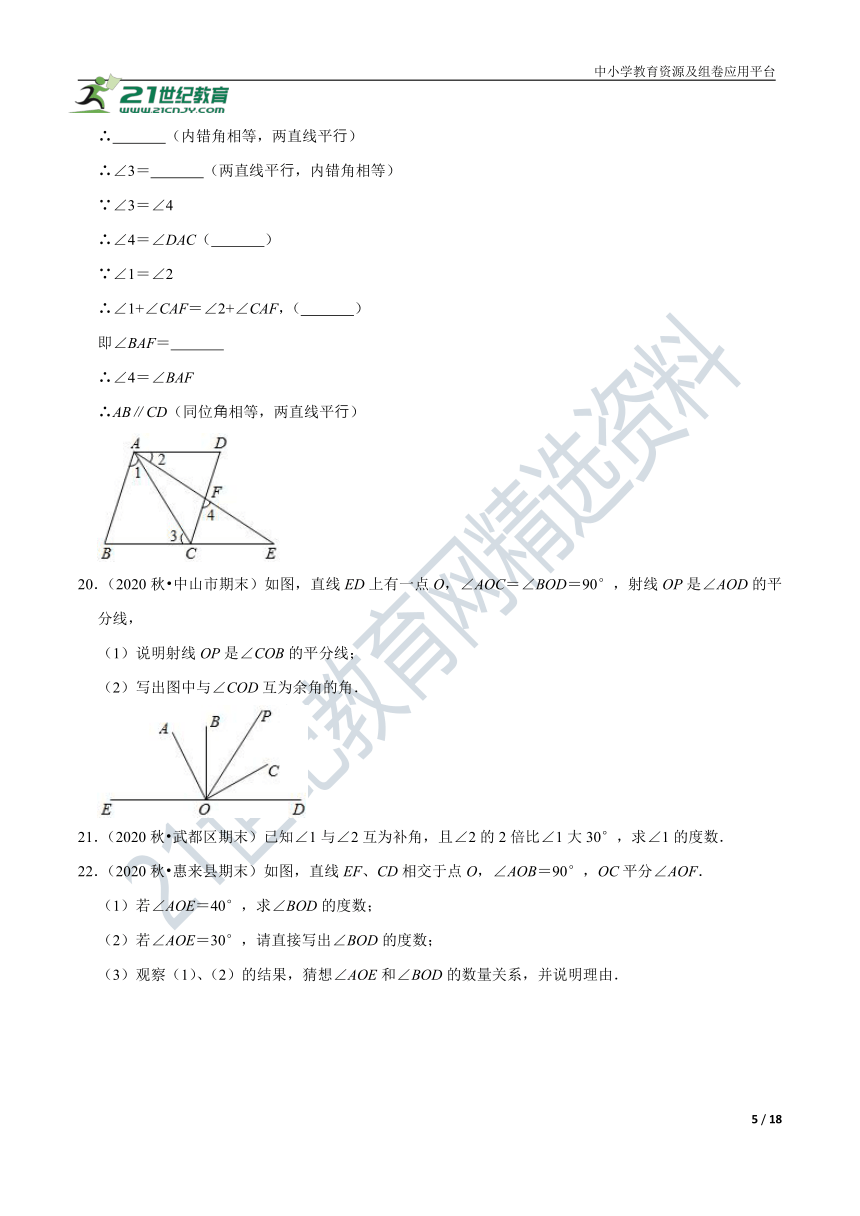
16.(2019春?下城区期末)如图,点E在AD的延长线上,下列四个条件:①∠1=∠2;②∠C+∠ABC=180°;③∠C=∠CDE;④∠3=∠4,能判断AB∥CD的是 (填序号).
17.(2020春?定远县期末)如图,将一副三角板按如图放置,则下列结论:①∠1=∠3;②如果∠2=30°,则有AC∥DE;③如果∠2=30°,则有BC∥AD;④如果∠2=30°,必有∠4=∠C.其中正确的有 .(填序号)
18.(2015春?南京校级期中)已知一个角的两边分别垂直于另一个角的两边,且这两个角的差是30°,则这两个角的度数分别是 .
三、解答题(本大题共8小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020春?南开区校级月考)填空:已知:如图,B、C、E三点在同一直线上,A、F、E三点在同一直线上,∠1=∠2=∠E,∠3=∠4.求证:AB∥CD.
证明:∵∠2=∠E
∴ (内错角相等,两直线平?)
∴∠3= (两直线平?,内错角相等)
∵∠3=∠4
∴∠4=∠DAC( )
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAF,( )
即∠BAF=
∴∠4=∠BAF
∴AB∥CD(同位?相等,两直线平?)
20.(2020秋?中山市期末)如图,直线ED上有一点O,∠AOC=∠BOD=90°,射线OP是∠AOD的平分线,
(1)说明射线OP是∠COB的平分线;
(2)写出图中与∠COD互为余角的角.
21.(2020秋?武都区期末)已知∠1与∠2互为补角,且∠2的2倍比∠1大30°,求∠1的度数.
22.(2020秋?惠来县期末)如图,直线EF、CD相交于点O,∠AOB=90°,OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=30°,请直接写出∠BOD的度数;
(3)观察(1)、(2)的结果,猜想∠AOE和∠BOD的数量关系,并说明理由.
23.(2019秋?天桥区期末)如图所示,已知AD∥BC,BE平分∠ABC,∠A=110°.求∠ADB的度数.
24.(2020秋?台儿庄区期末)将△ABC纸片沿DE折叠,其中∠B=∠C.
(1)如图1,点C落在BC边上的点F处,AB与DF是否平行?请说明理由;
(2)如图2,点C落在四边形ABCD内部的点G处,探索∠B与∠1+∠2之间的数量关系,并说明理由.
25.(2020秋?南岗区期末)已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
26.(2020春?汉阳区校级期中)如图1所示,MN∥PQ,∠B与MN,PQ分别交于A、C两点.
(1)若∠MAB=30°,∠QCB=20°,求∠B的度数;
(2)如图2所示,直线AE,CD相交于D点,且满足∠BAM=n∠MAE,∠BCP=n∠DCP.
①当n=2时,若∠ABC=90°,求∠CDA的度数;
②试探究∠CDA与∠B的关系.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】∠AOB=∠COD=90°,∠AOD=146°
则∠BOC=360°﹣2×90°﹣146°=34°
则∠BOC=34°.
故选:B.
2.【解析】∵∠EOF=90°,
∴∠COE+∠COF=90°,∠AOE+∠BOF=180°﹣∠EOF=90°,
∴∠AOE和∠BOF互余,
∵OE平分∠AOC,
∴∠AOE=∠COE,
∴∠COF=∠BOF,
∠COF和∠AOE互余,
故选:B.
3.【解析】∵∠1和∠2互为余角,∠1=60°,
∴∠2=90°﹣∠1=90°﹣60°=30°,
∵∠2与∠3互补,
∴∠3=180°﹣∠2=180°﹣30°=150°.
故选:D.
4.【解析】A、∠B的内错角是∠1,故此选项符合题意;
B、∠B与∠2是同旁内角,故此选项不合题意;
C、∠B与∠3是同位角,故此选项不合题意;
D、∠B与∠4是不是内错角,故此选项不合题意;
故选:A.
5.【解析】如图,CP⊥AB,垂足为P,
在P处开水渠,则水渠最短.
因为直线外一点与直线上各点连线的所有线段中,垂线段最短.
故选:C.
6.【解析】∵OM平分∠BOD,∠BOD=42°,
∴∠BOM=12∠BOD=12×42°=21°,
∴∠AOM=180°﹣∠BOM=159°,
故选:C.
7.【解析】A、对顶角相等,是真命题;
B、两点之间,线段最短,是真命题;
C、互补的两个角不一定相等,是真命题;
D、两直线平行,同位角相等,本选项说法是假命题;
故选:D.
8.【解析】①∵∠1=∠2不能得到l1∥l2,故本条件不合题意;
②∵∠4=∠5,∴l1∥l2,故本条件符合题意;
③∵∠2+∠5=180°不能得到l1∥l2,故本条件不合题意;
④∵∠1=∠3,∴l1∥l2,故本条件符合题意;
⑤∵∠6=∠2+∠3=∠1+∠2,∴∠1=∠3,∴l1∥l2,故本条件符合题意.
故选:C.
9.【解析】如图,
当AC∥DE时,∠BAD=∠DAE=45°;
当BC∥AD时,∠DAB=∠B=60°;
当BC∥AE时,∵∠EAB=∠B=60°,
∴∠BAD=∠DAE+∠EAB=45°+60°=105°;
当AB∥DE时,∵∠E=∠EAB=90°,
∴∠BAD=∠DAE+∠EAB=45°+90°=135°.
故选:B.
10.【解析】2条直线相交最多有1个交点,1=12×1×2,
3条直线相交最多有3个交点,3=1+2=12×2×3,
4条直线相交最多有6个交点,6=1+2+3=12×3×4,
5条直线相交最多有10个交点,10=1+2+3+4=12×4×5,
…
n条直线相交最多有交点的个数是:12n(n﹣1).
20条直线相交最多有交点的个数是:12n(n﹣1)=12×20×19=190.
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】两条直线相交所构成的四个角,
①因为有三个角都相等,都等于90°,所以能判定这两条直线垂直;
②因为有一对对顶角相等,但不一定等于90°,所以不能判定这两条直线垂直;
③有一个角是直角,能判定这两条直线垂直;
④因为一对邻补角相加等于180°,这对邻补角又相等都等于90°,所以能判定这两条直线垂直;
故答案为:①③④.
12.【解析】∵一个角的12等于另一个角的13,
∴这两个角不相等,
设其中一个角的度数为x°,另一个角的度数为12x°÷13=32x°,
∵两个角的两边两两互相平行,
∴x+32x=180,
解得:x=72,
即较小角的度数是72°,
故选:72.
13.【解析】∵OP∥QR∥ST,∠2=100°,∠3=120°,
∴∠2+∠PRQ=180°,∠3=∠SRQ=120°,
∴∠PRQ=180°﹣100°=80°,
∴∠1=∠SRQ﹣∠PRQ=40°,
故答案是40°.
14.【解析】过点C作CD∥a,
∵a∥b,
∴CD∥a∥b,
∴∠1+∠ECD=180°,∠3+∠DCF=180°,
∵∠2=95°,∠3=150°,
∴∠1+∠2+∠3=360°,
∴∠1=360°﹣∠2﹣∠3=360°﹣150°﹣95°=115°,
故答案为:115°.
15.【解析】延长ED交AG于点H,
∵AG∥EF,
∴∠E=∠CHD,
∴∠CHD=∠CDE﹣∠DCG,
∵∠B﹣∠DCG=115°,∠B﹣∠CDE=10°,
∴∠CDE=∠B﹣10°,∠DCG=∠B﹣115°,
∴∠E=∠CHD=∠B﹣10°﹣(∠B﹣115°)=105°,
故答案为:105.
16.【解析】①由∠1=∠2,可以判定AB∥CD.
②由∠C+∠ABC=180°,可以判定AB∥CD.
③由∠C=∠CDE,可以判定BC∥AD.
④由∠3=∠4,可以判定BC∥AD.
故答案为①②.
17.【解析】①∵∠CAB=∠EAD=90°,
∴∠1=∠CAB﹣∠2,∠3=∠EAD﹣∠2,
∴∠1=∠3.
∴①正确.
②∵∠2=30°,
∴∠1=90°﹣30°=60°,
∵∠E=60°,
∴∠1=∠E,
∴AC∥DE.
∴②正确.
③∵∠2=30°,
∴∠3=90°﹣30°=60°,
∵∠B=45°,
∴BC不平行于AD.
∴③错误.
④由②得AC∥DE.
∴∠4=∠C.
∴④正确.
故答案为:①②④.
18.【解析】∵一个角的两边分别垂直于另一个角的两边,
∴这两个角相等或互补.
又∵这两个角的差是30°,
∴这两个角互补.
设一个角为x,则另一个角为x+30°,
根据题意可知:x+x+30°=180°.
解得:x=75°,x+30°=75°+30°=105°.
故答案为:75°、105°.
三、解答题(本大题共8小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.【解答】证明:∵∠2=∠E,
∴AD∥BC(内错角相等,两直线平行),
∴∠3=∠DAC(两直线平行,内错角相等),
∵∠3=∠4,
∴∠4=∠DAC(等量代换),
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAF(等式性质),
即∠BAF=∠DAC,
∴∠4=∠BAF,
∴AB∥CD(同位?相等,两直线平行).
故答案为:AD∥BC,∠DAC,等量代换,等式性质,∠DAC.
20.【解析】(1)∵∠AOC=∠BOD=90°,
∴∠AOD﹣∠AOC=∠AOD﹣90°=∠AOD﹣∠BOD,
∴∠COD=∠AOB,
∵射线OP是∠AOD的平分线;
∴∠POA=∠POD,
∴∠POA﹣∠AOB=∠POD﹣∠COD,
∴∠POB=∠POC,
∴射线OP是∠COB的平分线;
(2)∵∠COD=∠AOB,∠AOC=∠BOD=90°,
∴∠AOE=∠BOC,
∵∠COD+∠BOC=90°,
∴图中与∠COD互为余角的角有∠BOC和∠AOE.
21.【解析】由∠1与∠2互为补角,得∠2=180°﹣∠1,
由∠2的2倍比∠1大30°,得2(180°﹣∠1)=∠1+30°,
解得∠1=110°.
22.【解析】(1)∵∠AOE+∠AOF=180°,∠AOE=40°,
∴∠AOF=180°﹣∠AOE=140°
∵OC平分∠AOF,
∴∠AOC=12∠AOF=12×140°=70°
∵∠AOB=90°
∴∠BOD=180°﹣∠AOC﹣∠AOB=180°﹣70°﹣90°=20°
(2)方法同(1)可得,若∠AOE=30°,则∠BOD=15°
(3)猜想:∠BOD=12∠AOE,
理由如下:
∵OC平分∠AOF
∴∠AOC=12∠AOF
∵∠AOE+∠AOF=180°,
∴∠AOF=180°﹣∠AOE
∵∠BOD+∠AOB+∠AOC=180°,∠AOB=90°
∴∠BOD+90°+12∠AOF=180°,
∴∠BOD=90°-12∠AOF=90°﹣90°+12∠AOE=12∠AOE.
23.【解析】如图所示:
∵AD∥BC,
∴∠A+∠ABC=180°,∠ADB=∠CBD,
又∵∠A=110°,
∴∠ABC=180°﹣110°=70°,
又∵BE平分∠ABC,
∴∠CBD=12∠ABC
∴∠CBD=12×70°=35°
∴∠ADB=35°.
24.【解析】(1)AB与DF平行.理由如下:
由翻折,得∠DFC=∠C.
又∵∠B=∠C,
∴∠B=∠DFC,
∴AB∥DF.
(2)连接GC,如图所示.
由翻折,得∠DGE=∠ACB.
∵∠1=∠DGC+∠DCG,∠2=∠EGC+∠ECG,
∴∠1+∠2=∠DGC+∠DCG+∠EGC+∠ECG=(∠DGC+∠EGC)+(∠DCG+∠ECG)=∠DGE+∠DCE=2∠ACB.
∵∠B=∠ACB,
∴∠1+∠2=2∠B.
25.【解答】(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
26.【解析】(1)如图1,过点B作BF∥MN,
则∠BAM=∠ABF=30°,
∵MN∥PQ,
∴PQ∥BF,
∴∠CBF=∠QCB=20°,
∴∠ABC=∠ABF+∠CBF=50°;
(2)①设∠MAE=x°,∠DCP=y°,
当n=2时,∠BAM=2x°,∠BCP=2y°,
∴∠BCQ=180°﹣2y°,
由(1)知,∠ABC=∠BAM+∠BCQ,
∴2x+180﹣2y=90,整理,得:x﹣y=﹣45,
如图2,延长DA交PQ于点G,
∵MN∥PQ,
∴∠MAE=∠DGC=x°,
则∠CDA=∠DCP﹣∠DGC
=y°﹣x°
=﹣(x﹣y)°
=45°;
②n∠CDA+∠ABC=180°,
设∠MAE=x°,∠DCP=y°,则∠BAM=n∠MAE=nx°,∠BCP=n∠DCP=ny°,
∴∠BCQ=180°﹣ny°,
由(1)知,∠ABC=nx°+180°﹣ny°,
∴y°﹣x°=180°-∠ABCn,
∵MN∥PQ,
∴∠MAE=∠DGP=x°,
则∠CDA=∠DCP﹣∠DGC
=y°﹣x°
=180°-∠ABCn,
即n∠CDA+∠ABC=180°.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分120分,试题共26题,选择10道、填空8道、解答8道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020秋?玉田县期末)如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC的度数为( )
A.43° B.34° C.56° D.50°
2.(2020秋?鄂州期末)如图所示,点O在直线AB上,OE平分∠AOC,∠EOF=90°,则∠COF与∠AOE的关系是( )
A.相等 B.互余 C.互补 D.无法确定
3.(2020秋?新宾县期末)已知∠1和∠2互为余角,且∠2与∠3互补,∠1=60°,则∠3为( )
A.120° B.60° C.30° D.150°
4.(2020秋?长春期末)如图,∠B的内错角是( )
A.∠1 B.∠2 C.∠3 D.∠4
5.(2020春?威县期末)如图,把河AB中的水引到C,拟修水渠中最短的是( )
A.CM B.CN C.CP D.CQ
6.(2020秋?铁西区期末)如图,直线AB,CD相交于点O,射线OM平分∠BOD,若∠BOD=42°,则∠AOM等于( )
A.138° B.148° C.159° D.169°
7.(2020秋?龙岗区期末)下列命题中,是假命题的是( )
A.对顶角相等
B.两点之间,线段最短
C.互补的两个角不一定相等
D.同位角相等
8.(2020春?兴国县期末)如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l1∥l2的有( )
A.5个 B.4个 C.3个 D.2个
9.(2019秋?昌平区校级期末)一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时,BC∥DE,则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为( )
A.60°和135° B.45°、60°、105°和135°
C.30°和45° D.以上都有可能
10.(2020秋?邢台期中)观察如图,并阅读图形下面的相关文字:
两条直线相交,最多有1个交点;三条直线相交,最多有3个交点;4条直线相交,最多有6个交点……
像这样,20条直线相交,交点最多的个数是( )
A.100个 B.135个 C.190个 D.200个
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020秋?肇源县期末)两条直线相交所构成的四个角,其中:①有三个角都相等;②有一对对顶角相等;③有一个角是直角;④有一对邻补角相等,能判定这两条直线垂直的有 .
12.(2020秋?香坊区期末)两个角的两边两两互相平行,且一个角的12等于另一个角的13,则这两个角中较小角的度数为 °.
13.(2020秋?德惠市期末)如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1= .
14.(2020?安徽一模)如图,a∥b,∠2=95°,∠3=150°,则∠1的度数是 .
15.(2020春?巴南区期末)小张同学观察如图1所示的北斗七星图,小张同学把北斗七星:摇光、开阳、玉衡、天权、天玑、天璇、天枢按图2分别标为点A,B,C,D,E,F,G,然后将点A,B,C,D,E,F,G顺次首尾连接,发现AG恰好经过点C,且∠B﹣∠DCG=115°,∠B﹣∠D=10°,若AG∥EF,则∠E=m°,这里的m= .
16.(2019春?下城区期末)如图,点E在AD的延长线上,下列四个条件:①∠1=∠2;②∠C+∠ABC=180°;③∠C=∠CDE;④∠3=∠4,能判断AB∥CD的是 (填序号).
17.(2020春?定远县期末)如图,将一副三角板按如图放置,则下列结论:①∠1=∠3;②如果∠2=30°,则有AC∥DE;③如果∠2=30°,则有BC∥AD;④如果∠2=30°,必有∠4=∠C.其中正确的有 .(填序号)
18.(2015春?南京校级期中)已知一个角的两边分别垂直于另一个角的两边,且这两个角的差是30°,则这两个角的度数分别是 .
三、解答题(本大题共8小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020春?南开区校级月考)填空:已知:如图,B、C、E三点在同一直线上,A、F、E三点在同一直线上,∠1=∠2=∠E,∠3=∠4.求证:AB∥CD.
证明:∵∠2=∠E
∴ (内错角相等,两直线平?)
∴∠3= (两直线平?,内错角相等)
∵∠3=∠4
∴∠4=∠DAC( )
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAF,( )
即∠BAF=
∴∠4=∠BAF
∴AB∥CD(同位?相等,两直线平?)
20.(2020秋?中山市期末)如图,直线ED上有一点O,∠AOC=∠BOD=90°,射线OP是∠AOD的平分线,
(1)说明射线OP是∠COB的平分线;
(2)写出图中与∠COD互为余角的角.
21.(2020秋?武都区期末)已知∠1与∠2互为补角,且∠2的2倍比∠1大30°,求∠1的度数.
22.(2020秋?惠来县期末)如图,直线EF、CD相交于点O,∠AOB=90°,OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=30°,请直接写出∠BOD的度数;
(3)观察(1)、(2)的结果,猜想∠AOE和∠BOD的数量关系,并说明理由.
23.(2019秋?天桥区期末)如图所示,已知AD∥BC,BE平分∠ABC,∠A=110°.求∠ADB的度数.
24.(2020秋?台儿庄区期末)将△ABC纸片沿DE折叠,其中∠B=∠C.
(1)如图1,点C落在BC边上的点F处,AB与DF是否平行?请说明理由;
(2)如图2,点C落在四边形ABCD内部的点G处,探索∠B与∠1+∠2之间的数量关系,并说明理由.
25.(2020秋?南岗区期末)已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
26.(2020春?汉阳区校级期中)如图1所示,MN∥PQ,∠B与MN,PQ分别交于A、C两点.
(1)若∠MAB=30°,∠QCB=20°,求∠B的度数;
(2)如图2所示,直线AE,CD相交于D点,且满足∠BAM=n∠MAE,∠BCP=n∠DCP.
①当n=2时,若∠ABC=90°,求∠CDA的度数;
②试探究∠CDA与∠B的关系.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】∠AOB=∠COD=90°,∠AOD=146°
则∠BOC=360°﹣2×90°﹣146°=34°
则∠BOC=34°.
故选:B.
2.【解析】∵∠EOF=90°,
∴∠COE+∠COF=90°,∠AOE+∠BOF=180°﹣∠EOF=90°,
∴∠AOE和∠BOF互余,
∵OE平分∠AOC,
∴∠AOE=∠COE,
∴∠COF=∠BOF,
∠COF和∠AOE互余,
故选:B.
3.【解析】∵∠1和∠2互为余角,∠1=60°,
∴∠2=90°﹣∠1=90°﹣60°=30°,
∵∠2与∠3互补,
∴∠3=180°﹣∠2=180°﹣30°=150°.
故选:D.
4.【解析】A、∠B的内错角是∠1,故此选项符合题意;
B、∠B与∠2是同旁内角,故此选项不合题意;
C、∠B与∠3是同位角,故此选项不合题意;
D、∠B与∠4是不是内错角,故此选项不合题意;
故选:A.
5.【解析】如图,CP⊥AB,垂足为P,
在P处开水渠,则水渠最短.
因为直线外一点与直线上各点连线的所有线段中,垂线段最短.
故选:C.
6.【解析】∵OM平分∠BOD,∠BOD=42°,
∴∠BOM=12∠BOD=12×42°=21°,
∴∠AOM=180°﹣∠BOM=159°,
故选:C.
7.【解析】A、对顶角相等,是真命题;
B、两点之间,线段最短,是真命题;
C、互补的两个角不一定相等,是真命题;
D、两直线平行,同位角相等,本选项说法是假命题;
故选:D.
8.【解析】①∵∠1=∠2不能得到l1∥l2,故本条件不合题意;
②∵∠4=∠5,∴l1∥l2,故本条件符合题意;
③∵∠2+∠5=180°不能得到l1∥l2,故本条件不合题意;
④∵∠1=∠3,∴l1∥l2,故本条件符合题意;
⑤∵∠6=∠2+∠3=∠1+∠2,∴∠1=∠3,∴l1∥l2,故本条件符合题意.
故选:C.
9.【解析】如图,
当AC∥DE时,∠BAD=∠DAE=45°;
当BC∥AD时,∠DAB=∠B=60°;
当BC∥AE时,∵∠EAB=∠B=60°,
∴∠BAD=∠DAE+∠EAB=45°+60°=105°;
当AB∥DE时,∵∠E=∠EAB=90°,
∴∠BAD=∠DAE+∠EAB=45°+90°=135°.
故选:B.
10.【解析】2条直线相交最多有1个交点,1=12×1×2,
3条直线相交最多有3个交点,3=1+2=12×2×3,
4条直线相交最多有6个交点,6=1+2+3=12×3×4,
5条直线相交最多有10个交点,10=1+2+3+4=12×4×5,
…
n条直线相交最多有交点的个数是:12n(n﹣1).
20条直线相交最多有交点的个数是:12n(n﹣1)=12×20×19=190.
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】两条直线相交所构成的四个角,
①因为有三个角都相等,都等于90°,所以能判定这两条直线垂直;
②因为有一对对顶角相等,但不一定等于90°,所以不能判定这两条直线垂直;
③有一个角是直角,能判定这两条直线垂直;
④因为一对邻补角相加等于180°,这对邻补角又相等都等于90°,所以能判定这两条直线垂直;
故答案为:①③④.
12.【解析】∵一个角的12等于另一个角的13,
∴这两个角不相等,
设其中一个角的度数为x°,另一个角的度数为12x°÷13=32x°,
∵两个角的两边两两互相平行,
∴x+32x=180,
解得:x=72,
即较小角的度数是72°,
故选:72.
13.【解析】∵OP∥QR∥ST,∠2=100°,∠3=120°,
∴∠2+∠PRQ=180°,∠3=∠SRQ=120°,
∴∠PRQ=180°﹣100°=80°,
∴∠1=∠SRQ﹣∠PRQ=40°,
故答案是40°.
14.【解析】过点C作CD∥a,
∵a∥b,
∴CD∥a∥b,
∴∠1+∠ECD=180°,∠3+∠DCF=180°,
∵∠2=95°,∠3=150°,
∴∠1+∠2+∠3=360°,
∴∠1=360°﹣∠2﹣∠3=360°﹣150°﹣95°=115°,
故答案为:115°.
15.【解析】延长ED交AG于点H,
∵AG∥EF,
∴∠E=∠CHD,
∴∠CHD=∠CDE﹣∠DCG,
∵∠B﹣∠DCG=115°,∠B﹣∠CDE=10°,
∴∠CDE=∠B﹣10°,∠DCG=∠B﹣115°,
∴∠E=∠CHD=∠B﹣10°﹣(∠B﹣115°)=105°,
故答案为:105.
16.【解析】①由∠1=∠2,可以判定AB∥CD.
②由∠C+∠ABC=180°,可以判定AB∥CD.
③由∠C=∠CDE,可以判定BC∥AD.
④由∠3=∠4,可以判定BC∥AD.
故答案为①②.
17.【解析】①∵∠CAB=∠EAD=90°,
∴∠1=∠CAB﹣∠2,∠3=∠EAD﹣∠2,
∴∠1=∠3.
∴①正确.
②∵∠2=30°,
∴∠1=90°﹣30°=60°,
∵∠E=60°,
∴∠1=∠E,
∴AC∥DE.
∴②正确.
③∵∠2=30°,
∴∠3=90°﹣30°=60°,
∵∠B=45°,
∴BC不平行于AD.
∴③错误.
④由②得AC∥DE.
∴∠4=∠C.
∴④正确.
故答案为:①②④.
18.【解析】∵一个角的两边分别垂直于另一个角的两边,
∴这两个角相等或互补.
又∵这两个角的差是30°,
∴这两个角互补.
设一个角为x,则另一个角为x+30°,
根据题意可知:x+x+30°=180°.
解得:x=75°,x+30°=75°+30°=105°.
故答案为:75°、105°.
三、解答题(本大题共8小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.【解答】证明:∵∠2=∠E,
∴AD∥BC(内错角相等,两直线平行),
∴∠3=∠DAC(两直线平行,内错角相等),
∵∠3=∠4,
∴∠4=∠DAC(等量代换),
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAF(等式性质),
即∠BAF=∠DAC,
∴∠4=∠BAF,
∴AB∥CD(同位?相等,两直线平行).
故答案为:AD∥BC,∠DAC,等量代换,等式性质,∠DAC.
20.【解析】(1)∵∠AOC=∠BOD=90°,
∴∠AOD﹣∠AOC=∠AOD﹣90°=∠AOD﹣∠BOD,
∴∠COD=∠AOB,
∵射线OP是∠AOD的平分线;
∴∠POA=∠POD,
∴∠POA﹣∠AOB=∠POD﹣∠COD,
∴∠POB=∠POC,
∴射线OP是∠COB的平分线;
(2)∵∠COD=∠AOB,∠AOC=∠BOD=90°,
∴∠AOE=∠BOC,
∵∠COD+∠BOC=90°,
∴图中与∠COD互为余角的角有∠BOC和∠AOE.
21.【解析】由∠1与∠2互为补角,得∠2=180°﹣∠1,
由∠2的2倍比∠1大30°,得2(180°﹣∠1)=∠1+30°,
解得∠1=110°.
22.【解析】(1)∵∠AOE+∠AOF=180°,∠AOE=40°,
∴∠AOF=180°﹣∠AOE=140°
∵OC平分∠AOF,
∴∠AOC=12∠AOF=12×140°=70°
∵∠AOB=90°
∴∠BOD=180°﹣∠AOC﹣∠AOB=180°﹣70°﹣90°=20°
(2)方法同(1)可得,若∠AOE=30°,则∠BOD=15°
(3)猜想:∠BOD=12∠AOE,
理由如下:
∵OC平分∠AOF
∴∠AOC=12∠AOF
∵∠AOE+∠AOF=180°,
∴∠AOF=180°﹣∠AOE
∵∠BOD+∠AOB+∠AOC=180°,∠AOB=90°
∴∠BOD+90°+12∠AOF=180°,
∴∠BOD=90°-12∠AOF=90°﹣90°+12∠AOE=12∠AOE.
23.【解析】如图所示:
∵AD∥BC,
∴∠A+∠ABC=180°,∠ADB=∠CBD,
又∵∠A=110°,
∴∠ABC=180°﹣110°=70°,
又∵BE平分∠ABC,
∴∠CBD=12∠ABC
∴∠CBD=12×70°=35°
∴∠ADB=35°.
24.【解析】(1)AB与DF平行.理由如下:
由翻折,得∠DFC=∠C.
又∵∠B=∠C,
∴∠B=∠DFC,
∴AB∥DF.
(2)连接GC,如图所示.
由翻折,得∠DGE=∠ACB.
∵∠1=∠DGC+∠DCG,∠2=∠EGC+∠ECG,
∴∠1+∠2=∠DGC+∠DCG+∠EGC+∠ECG=(∠DGC+∠EGC)+(∠DCG+∠ECG)=∠DGE+∠DCE=2∠ACB.
∵∠B=∠ACB,
∴∠1+∠2=2∠B.
25.【解答】(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
26.【解析】(1)如图1,过点B作BF∥MN,
则∠BAM=∠ABF=30°,
∵MN∥PQ,
∴PQ∥BF,
∴∠CBF=∠QCB=20°,
∴∠ABC=∠ABF+∠CBF=50°;
(2)①设∠MAE=x°,∠DCP=y°,
当n=2时,∠BAM=2x°,∠BCP=2y°,
∴∠BCQ=180°﹣2y°,
由(1)知,∠ABC=∠BAM+∠BCQ,
∴2x+180﹣2y=90,整理,得:x﹣y=﹣45,
如图2,延长DA交PQ于点G,
∵MN∥PQ,
∴∠MAE=∠DGC=x°,
则∠CDA=∠DCP﹣∠DGC
=y°﹣x°
=﹣(x﹣y)°
=45°;
②n∠CDA+∠ABC=180°,
设∠MAE=x°,∠DCP=y°,则∠BAM=n∠MAE=nx°,∠BCP=n∠DCP=ny°,
∴∠BCQ=180°﹣ny°,
由(1)知,∠ABC=nx°+180°﹣ny°,
∴y°﹣x°=180°-∠ABCn,
∵MN∥PQ,
∴∠MAE=∠DGP=x°,
则∠CDA=∠DCP﹣∠DGC
=y°﹣x°
=180°-∠ABCn,
即n∠CDA+∠ABC=180°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
