五年级下册数学课件 第三单元《第3课时 长方体的表面积》人教版 (共27张PPT)
文档属性
| 名称 | 五年级下册数学课件 第三单元《第3课时 长方体的表面积》人教版 (共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 566.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
第三单元
第3课时
长方体的表面积
人教版数学五年级下册
学习目标
1.理解长方体表面积的意义。
2.掌握长方体表面积的计算方法,能够正确地进行计算,并能运用所学知识解决一些实际问题。
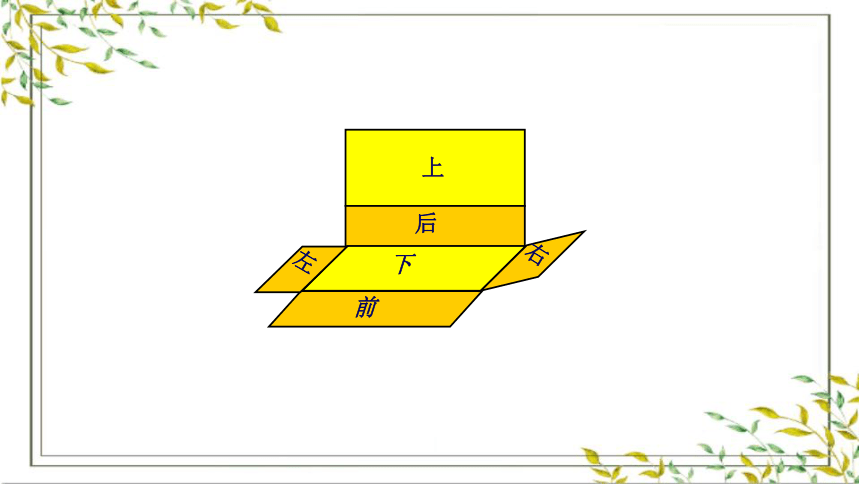
同学们,我们上节课已经认识了长方体,知道它们是由6个长方形围成的立体图形。那么它们都有哪些特征?
导入新知
长方体有6个面,12条棱,8个顶点,相对的面完全相同,相对的棱长度相等。
同学们,你们都已经掌握了长方体的特征。那么今天我们继续来研究长方体,一起来探究一下长方体的表面积。
长方体的表面积
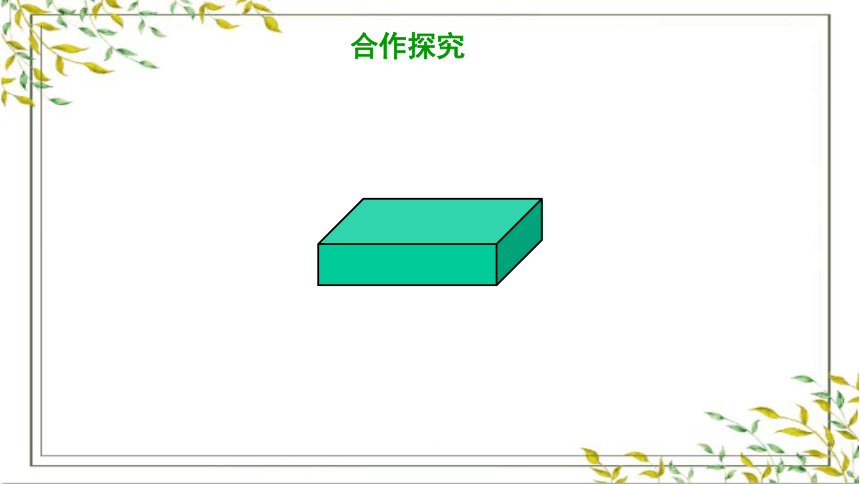
合作探究
上
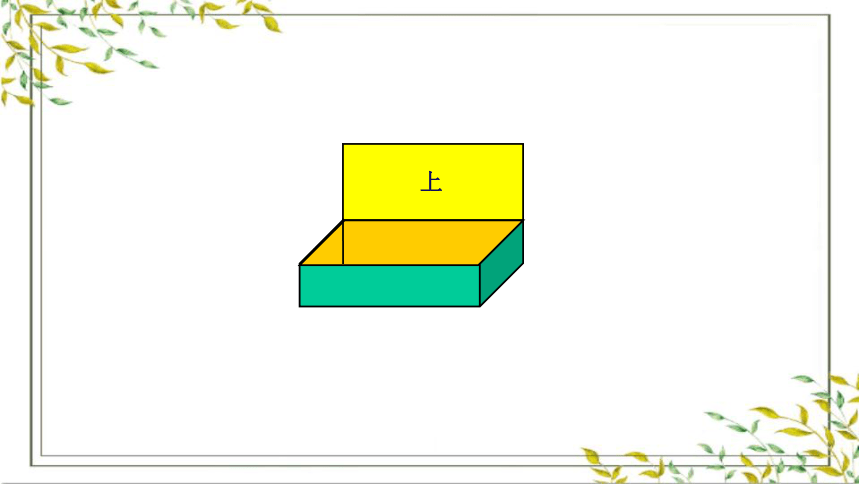
上
下
前
后
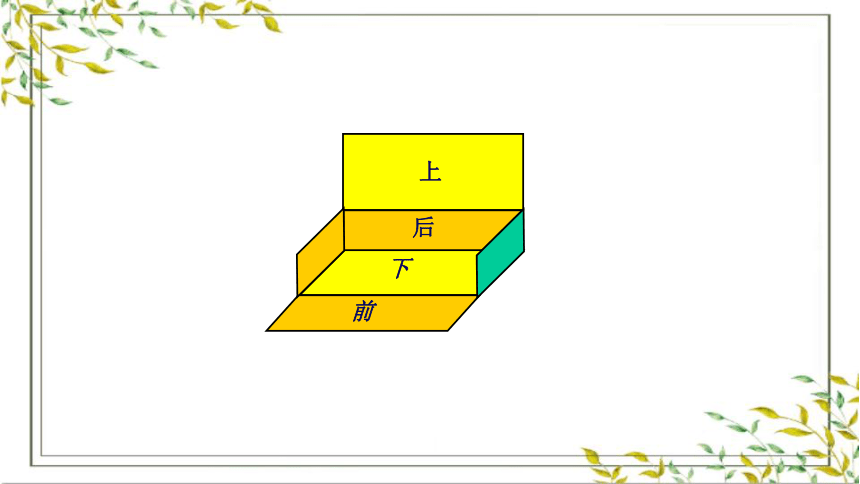
上
下
前
后
左
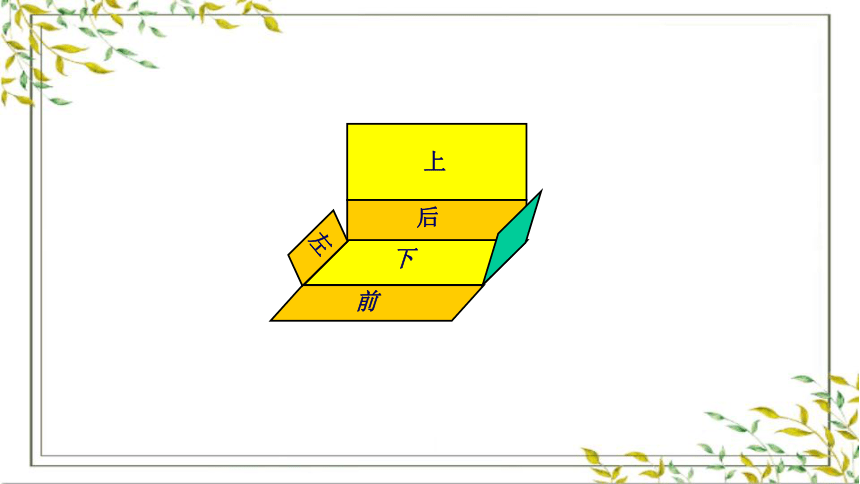
上
下
前
后
左
右
上
下
前
后
左
右
上
下
前
后
左
右
下
前
后
上
左
右
上
下
前
后
左
右
什么叫长方体的表面积?
长方体6个面的总面积,叫做它的表面积。
合作探究
上
右
前
长方体的表面积怎样计算?
(1)它上、下每个面的长是_________,宽是________,
面积是
。
10厘米(长)
6厘米(宽)
2厘米(高)
10厘米
6厘米
60平方厘米
总结:长方体上面(或下面)的面积=长×宽
(2)它前、后每个面的长是_________,宽是________,
面积是
。
10厘米(长)
6厘米(宽)
10厘米
2厘米
20平方厘米
总结:长方体前面(或后面)的面积=长×高
2厘米(高)
(3)它左、右每个面的长是_________,宽是________,
面积是
。
10厘米(长)
6厘米(宽)
6厘米
2厘米
12平方厘米
总结:长方体左面(或右面)的面积=宽×高
2厘米(高)
做一个微波炉的包装箱,(如右图),至少要用多少平方米的硬纸板?
上、下每个面,长______,宽_______,面积是__________;
前、后每个面,长______,宽_______,面积是__________;
左、右每个面,长______,宽_______,面积是__________。
这个包装箱的表面积是:
0.7m
0.5m
0.35m2
0.7m
0.4m
0.28m2
0.5m
0.4m
0.2m2
0.7×0.5×2+0.7×0.4×2+0.5×0.4×2
=
0.7+0.56+0.4
=1.66(平方米)
答:至少要用1.66平方米的硬纸板。
做一个微波炉的包装箱,(如右图),至少要用多少平方米的硬纸板?
上、下每个面,长______,宽_______,面积是__________;
前、后每个面,长______,宽_______,面积是__________;
左、右每个面,长______,宽_______,面积是__________。
这个包装箱的表面积是:
0.7m
0.5m
0.35m2
0.7m
0.4m
0.28m2
0.5m
0.4m
0.2m2
(0.7×0.5+0.7×0.4+0.5×0.4)×2
=
0.83×2
=1.66(平方米)
答:至少要用1.66平方米的硬纸板。
(0.7×0.5+0.7×0.4+0.5×0.4)×2
0.7×0.5×2+0.7×0.4×2+0.5×0.4×2
比较两种方法有什么不同?他们之间有什么联系?
上
和下
前
和后
右
和左
长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2
上(或下)
前(或后)
右(或左)
长方体的表面积=(长×宽+长×高+高×宽)×
2
长方体的表面积=
(长×宽+长×高+宽×高)×2
(6×5+6×4+5×4)
×2
=
(30+24+20)
×2
=
74×2
=148(平方厘米)
答:至少要用148平方厘米硬纸板。
1.做一个长6厘米,宽5厘米,高4厘米的长方体纸盒,至少要用多少平方厘米硬纸板?
6厘米
4厘米
5厘米
巩固新知
2.
一个长方体无盖塑料盒,长4米,宽3米,高2.5米。它的表面积是多少平方米?
4米
2.5米
3米
=12+20+15
=47(平方米)
4×3+4×2.5×2+3×2.5×2
答:无盖塑料盒的表面积是47平方米。
长方体的表面积=
(长×宽+长×高+宽×高)×2
课堂总结
1.光华街口装了一个新的长方体铁皮邮箱,长50cm、宽40cm、
高78cm。做这个邮箱至少需要多少平方厘米的铁皮?
(50
×
40+50
×
78+40
×
78)
×2
=(2000+3900+3120)
×2
=9020
×2
=18040(平方厘米)
答:做这个邮箱至少需要18040平方厘米的铁皮。
课后练习
2.一个长方体的饼干盒,长10cm、宽6cm、高12cm。如果围着它贴一圈商标纸(上下面不贴),这张商标纸的面积至少多少平方厘米?
(10
×
12+6
×
12)
×2
=(120+72)
×2
=192
×2
=384(平方厘米)
答:这张商标纸的面积至少384平方厘米。
再
见
第三单元
第3课时
长方体的表面积
人教版数学五年级下册
学习目标
1.理解长方体表面积的意义。
2.掌握长方体表面积的计算方法,能够正确地进行计算,并能运用所学知识解决一些实际问题。
同学们,我们上节课已经认识了长方体,知道它们是由6个长方形围成的立体图形。那么它们都有哪些特征?
导入新知
长方体有6个面,12条棱,8个顶点,相对的面完全相同,相对的棱长度相等。
同学们,你们都已经掌握了长方体的特征。那么今天我们继续来研究长方体,一起来探究一下长方体的表面积。
长方体的表面积
合作探究
上
上
下
前
后
上
下
前
后
左
上
下
前
后
左
右
上
下
前
后
左
右
上
下
前
后
左
右
下
前
后
上
左
右
上
下
前
后
左
右
什么叫长方体的表面积?
长方体6个面的总面积,叫做它的表面积。
合作探究
上
右
前
长方体的表面积怎样计算?
(1)它上、下每个面的长是_________,宽是________,
面积是
。
10厘米(长)
6厘米(宽)
2厘米(高)
10厘米
6厘米
60平方厘米
总结:长方体上面(或下面)的面积=长×宽
(2)它前、后每个面的长是_________,宽是________,
面积是
。
10厘米(长)
6厘米(宽)
10厘米
2厘米
20平方厘米
总结:长方体前面(或后面)的面积=长×高
2厘米(高)
(3)它左、右每个面的长是_________,宽是________,
面积是
。
10厘米(长)
6厘米(宽)
6厘米
2厘米
12平方厘米
总结:长方体左面(或右面)的面积=宽×高
2厘米(高)
做一个微波炉的包装箱,(如右图),至少要用多少平方米的硬纸板?
上、下每个面,长______,宽_______,面积是__________;
前、后每个面,长______,宽_______,面积是__________;
左、右每个面,长______,宽_______,面积是__________。
这个包装箱的表面积是:
0.7m
0.5m
0.35m2
0.7m
0.4m
0.28m2
0.5m
0.4m
0.2m2
0.7×0.5×2+0.7×0.4×2+0.5×0.4×2
=
0.7+0.56+0.4
=1.66(平方米)
答:至少要用1.66平方米的硬纸板。
做一个微波炉的包装箱,(如右图),至少要用多少平方米的硬纸板?
上、下每个面,长______,宽_______,面积是__________;
前、后每个面,长______,宽_______,面积是__________;
左、右每个面,长______,宽_______,面积是__________。
这个包装箱的表面积是:
0.7m
0.5m
0.35m2
0.7m
0.4m
0.28m2
0.5m
0.4m
0.2m2
(0.7×0.5+0.7×0.4+0.5×0.4)×2
=
0.83×2
=1.66(平方米)
答:至少要用1.66平方米的硬纸板。
(0.7×0.5+0.7×0.4+0.5×0.4)×2
0.7×0.5×2+0.7×0.4×2+0.5×0.4×2
比较两种方法有什么不同?他们之间有什么联系?
上
和下
前
和后
右
和左
长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2
上(或下)
前(或后)
右(或左)
长方体的表面积=(长×宽+长×高+高×宽)×
2
长方体的表面积=
(长×宽+长×高+宽×高)×2
(6×5+6×4+5×4)
×2
=
(30+24+20)
×2
=
74×2
=148(平方厘米)
答:至少要用148平方厘米硬纸板。
1.做一个长6厘米,宽5厘米,高4厘米的长方体纸盒,至少要用多少平方厘米硬纸板?
6厘米
4厘米
5厘米
巩固新知
2.
一个长方体无盖塑料盒,长4米,宽3米,高2.5米。它的表面积是多少平方米?
4米
2.5米
3米
=12+20+15
=47(平方米)
4×3+4×2.5×2+3×2.5×2
答:无盖塑料盒的表面积是47平方米。
长方体的表面积=
(长×宽+长×高+宽×高)×2
课堂总结
1.光华街口装了一个新的长方体铁皮邮箱,长50cm、宽40cm、
高78cm。做这个邮箱至少需要多少平方厘米的铁皮?
(50
×
40+50
×
78+40
×
78)
×2
=(2000+3900+3120)
×2
=9020
×2
=18040(平方厘米)
答:做这个邮箱至少需要18040平方厘米的铁皮。
课后练习
2.一个长方体的饼干盒,长10cm、宽6cm、高12cm。如果围着它贴一圈商标纸(上下面不贴),这张商标纸的面积至少多少平方厘米?
(10
×
12+6
×
12)
×2
=(120+72)
×2
=192
×2
=384(平方厘米)
答:这张商标纸的面积至少384平方厘米。
再
见
