安徽省濉溪县2020—2021学年九年级上学期期末考试数学试卷(Word版,附图片答案)
文档属性
| 名称 | 安徽省濉溪县2020—2021学年九年级上学期期末考试数学试卷(Word版,附图片答案) |  | |
| 格式 | docx | ||
| 文件大小 | 901.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 13:38:34 | ||
图片预览


文档简介
濉溪县 2020—2021学年度第一学期期末考试
九 年 级 数 学 试卷
选择题(本题共10 小题,每小题3分,满分 30 分)
1.下列图形中,既是轴对称图形,又是中心对称图形的个数有
A.1个 B.2 个 C.3 个 D.4个
2.若α锐角,且 sin(α—10°)=false,则α等于
A.80° B.70° C.60° D.50°
若 3x-4y=0,则下列式子正确的是
A.false B.false C.false D .false
4.关于二次函数y=2x?+4x-1,下列说法正确的是
A.图象与y轴的交点坐标为(0,1) B. 图象的对称轴在 y 轴的右侧
C. 当 x<0 时,y 随z 的增大而减小 D. y的最小值为-3
5.如图,在平行四边形 ABCD中,点E在边 DC上,DE∶EC=3∶1,连接AE交BD于点 F,则△DEF 的面积与△BAF 的面积之比为…
A.3:4 B.9 :1 C.9:16 D.3:1
6.如图,二次函数y=ax?+bx+c的最大值为3,一元二次方程ax?+bx+c-m=0有实数根,则 m 的取值范围是
A. m≥3 B.m≥-3 C.m≤3 D.m≤-3
7.如果某人沿坡度为3∶4的斜坡前进10m,那么他所在的位置比原来的位置升高了
A.6m B.8m C.10m D.12m
8.如图,点 A、B、C均在⊙O上,若∠OBC=40°,则∠A的度数是
A.65°
B.60°
C.55°
D.50°
如图,在△ABC中,点 D为BC边上的一点,且 AD=AB=2, AD⊥AB,过点 D作DE⊥AD,DE交AC于点E,若 DE=1,则△ABC 的面积为
A.false B.4
C.false D.8
10.如图,在 Rt△ABC中,∠A=90°,AC=6cm,AB=8cm,动点D从点A 出发,在 AB上以每秒1cm 的速度向点B运动,与此同时动点E从点B出发,在 BC边上以每秒2cm的速度向点C运动,记运动时间为x秒(0≤x≤5),△DEB的面积为y,则下列图象能正确反映 y 与x 之间的函数关系的是
二、填空题(本题共 4小题,每小题 4 分,满分 16 分)
11.已知 A(0,3),B(2,3)是抛物线 y=-x?+bx+c 上两点,该抛物线的解析式是
12.已知false,且a+b-2c=9,则a的值为_
13.如图,AB是⊙O的直径,AB=4,点 M是OA 的中点,过点 M的直线与⊙O交于C、D两点.若∠CMA=45°,则弦 CD的长为
14.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边 AC上,当AE=____时,以 A、D、E为顶点的三角形与△ABC相似
三、(本题共 2 小题,每小题5 分,满分 10 分)
15.计算∶falsecos? 45°-sin 30tan 60°-falsesin 60°
16.如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,垂足为 D,E.
(1)证明∶△ACD~△ABE;
(2)若将 D,E连接起来,则△AED与△ABC能相似吗? 说说你的理由
四、(本题共3 小题,每小题6分,满分18 分)
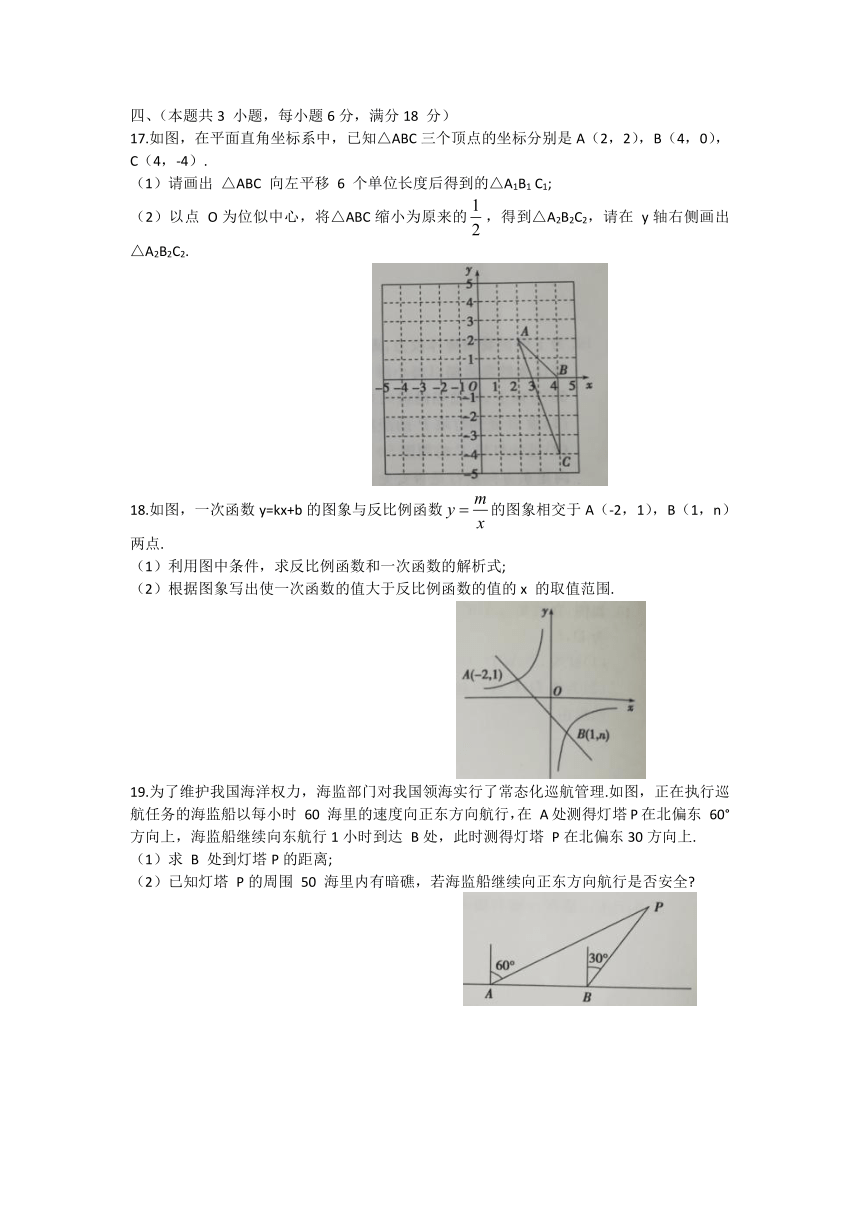
17.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,-4).
(1)请画出 △ABC 向左平移 6 个单位长度后得到的△A1B1 C1;
(2)以点 O为位似中心,将△ABC缩小为原来的false,得到△A2B2C2,请在 y轴右侧画出△A2B2C2.
18.如图,一次函数y=kx+b的图象与反比例函数false的图象相交于A(-2,1),B(1,n)两点.
(1)利用图中条件,求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x 的取值范围.
19.为了维护我国海洋权力,海监部门对我国领海实行了常态化巡航管理.如图,正在执行巡航任务的海监船以每小时 60 海里的速度向正东方向航行,在 A处测得灯塔P在北偏东 60°方向上,海监船继续向东航行1小时到达 B处,此时测得灯塔 P在北偏东30方向上.
(1)求 B 处到灯塔P的距离;
(2)已知灯塔 P的周围 50 海里内有暗礁,若海监船继续向正东方向航行是否安全?
五、(本题共 2 小题,每小题 8 分,满分 16 分)
20.已知∶如图,AB是⊙O的直径,点E为⊙O上一点,点D是上一点,连接 AE并延长至点C,使∠CBE=∠BDE,BD 与 AE 交于点F.
(1)求证∶BC 是⊙O的切线;
(2)若 BD 平分∠ABE,求证;AD2=DF*DB.
21.某商店购进一批单价为 16 元的日用品,销售一段时间后,为了获取更多利润,商店决定提高销售价格,经试验发现,若按每件 20 元的价格销售时,每月能卖 360 件;若按每件25元的价格销售时,每月能卖 210 件.假定每月销售件数 y(件)是价格x(元/件)的一次函数。
(1)试求 y与x 之间的函数关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格为多少时,才能使每月获得最大利润?每月的最大利润是多少?(总利润=总收入-总成本).
六、(本题满分 10 分)
22.如图,在正方形 ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转 90°得到线段 MN,在 CD边上取点P使CP=BM,连接 NP,BP.
(1)求证∶△ABM≌△BCP;
(2)求证∶四边形 BMNP 是平行四边形;
(3)线段 MN与CD 交于点Q,连接 AQ,若△MCQ~△AMQ,则 BM与 MC 存在怎样的数量关系?请说明理由.
九 年 级 数 学 试卷
选择题(本题共10 小题,每小题3分,满分 30 分)
1.下列图形中,既是轴对称图形,又是中心对称图形的个数有
A.1个 B.2 个 C.3 个 D.4个
2.若α锐角,且 sin(α—10°)=false,则α等于
A.80° B.70° C.60° D.50°
若 3x-4y=0,则下列式子正确的是
A.false B.false C.false D .false
4.关于二次函数y=2x?+4x-1,下列说法正确的是
A.图象与y轴的交点坐标为(0,1) B. 图象的对称轴在 y 轴的右侧
C. 当 x<0 时,y 随z 的增大而减小 D. y的最小值为-3
5.如图,在平行四边形 ABCD中,点E在边 DC上,DE∶EC=3∶1,连接AE交BD于点 F,则△DEF 的面积与△BAF 的面积之比为…
A.3:4 B.9 :1 C.9:16 D.3:1
6.如图,二次函数y=ax?+bx+c的最大值为3,一元二次方程ax?+bx+c-m=0有实数根,则 m 的取值范围是
A. m≥3 B.m≥-3 C.m≤3 D.m≤-3
7.如果某人沿坡度为3∶4的斜坡前进10m,那么他所在的位置比原来的位置升高了
A.6m B.8m C.10m D.12m
8.如图,点 A、B、C均在⊙O上,若∠OBC=40°,则∠A的度数是
A.65°
B.60°
C.55°
D.50°
如图,在△ABC中,点 D为BC边上的一点,且 AD=AB=2, AD⊥AB,过点 D作DE⊥AD,DE交AC于点E,若 DE=1,则△ABC 的面积为
A.false B.4
C.false D.8
10.如图,在 Rt△ABC中,∠A=90°,AC=6cm,AB=8cm,动点D从点A 出发,在 AB上以每秒1cm 的速度向点B运动,与此同时动点E从点B出发,在 BC边上以每秒2cm的速度向点C运动,记运动时间为x秒(0≤x≤5),△DEB的面积为y,则下列图象能正确反映 y 与x 之间的函数关系的是
二、填空题(本题共 4小题,每小题 4 分,满分 16 分)
11.已知 A(0,3),B(2,3)是抛物线 y=-x?+bx+c 上两点,该抛物线的解析式是
12.已知false,且a+b-2c=9,则a的值为_
13.如图,AB是⊙O的直径,AB=4,点 M是OA 的中点,过点 M的直线与⊙O交于C、D两点.若∠CMA=45°,则弦 CD的长为
14.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边 AC上,当AE=____时,以 A、D、E为顶点的三角形与△ABC相似
三、(本题共 2 小题,每小题5 分,满分 10 分)
15.计算∶falsecos? 45°-sin 30tan 60°-falsesin 60°
16.如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,垂足为 D,E.
(1)证明∶△ACD~△ABE;
(2)若将 D,E连接起来,则△AED与△ABC能相似吗? 说说你的理由
四、(本题共3 小题,每小题6分,满分18 分)
17.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,-4).
(1)请画出 △ABC 向左平移 6 个单位长度后得到的△A1B1 C1;
(2)以点 O为位似中心,将△ABC缩小为原来的false,得到△A2B2C2,请在 y轴右侧画出△A2B2C2.
18.如图,一次函数y=kx+b的图象与反比例函数false的图象相交于A(-2,1),B(1,n)两点.
(1)利用图中条件,求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x 的取值范围.
19.为了维护我国海洋权力,海监部门对我国领海实行了常态化巡航管理.如图,正在执行巡航任务的海监船以每小时 60 海里的速度向正东方向航行,在 A处测得灯塔P在北偏东 60°方向上,海监船继续向东航行1小时到达 B处,此时测得灯塔 P在北偏东30方向上.
(1)求 B 处到灯塔P的距离;
(2)已知灯塔 P的周围 50 海里内有暗礁,若海监船继续向正东方向航行是否安全?
五、(本题共 2 小题,每小题 8 分,满分 16 分)
20.已知∶如图,AB是⊙O的直径,点E为⊙O上一点,点D是上一点,连接 AE并延长至点C,使∠CBE=∠BDE,BD 与 AE 交于点F.
(1)求证∶BC 是⊙O的切线;
(2)若 BD 平分∠ABE,求证;AD2=DF*DB.
21.某商店购进一批单价为 16 元的日用品,销售一段时间后,为了获取更多利润,商店决定提高销售价格,经试验发现,若按每件 20 元的价格销售时,每月能卖 360 件;若按每件25元的价格销售时,每月能卖 210 件.假定每月销售件数 y(件)是价格x(元/件)的一次函数。
(1)试求 y与x 之间的函数关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格为多少时,才能使每月获得最大利润?每月的最大利润是多少?(总利润=总收入-总成本).
六、(本题满分 10 分)
22.如图,在正方形 ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转 90°得到线段 MN,在 CD边上取点P使CP=BM,连接 NP,BP.
(1)求证∶△ABM≌△BCP;
(2)求证∶四边形 BMNP 是平行四边形;
(3)线段 MN与CD 交于点Q,连接 AQ,若△MCQ~△AMQ,则 BM与 MC 存在怎样的数量关系?请说明理由.
同课章节目录
